数据分析专栏记录之 -基础数学与统计知识 2 概率论基础与python
数据分析专栏记录之 -基础数学与统计知识专栏记录:
2、概率论基础与python
前言
概率论与python,是一件很有趣的事情吧!!!
知识内容
# 离散分布
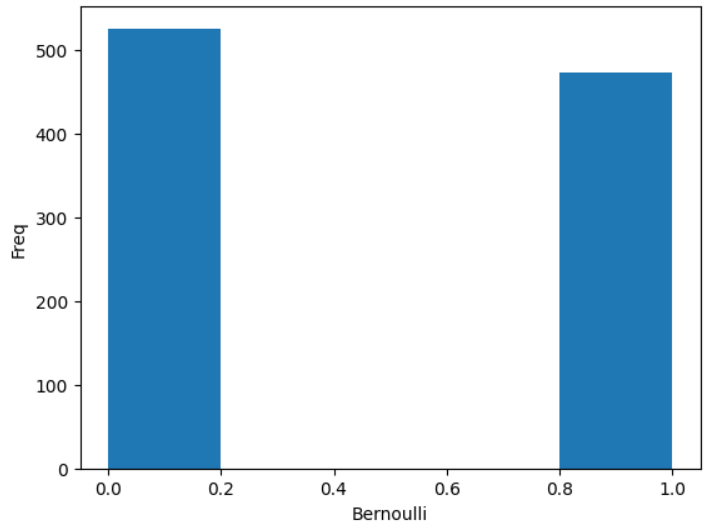
# ---伯努利分布 伯努利分布是针对单个观测结果的。
"""
我们有一个真的(1)的结果和一个假的(0)的结果。假设我们接受正面为真(我们可以选择正面为真或成功)。
那么,如果正面朝上的概率是 p ,相反情况的概率就是 1-p 。
"""import seaborn as sns
from scipy.stats import bernoulli# 单一观察值
# 生成数据(1000 points, possible outs: 1 or 0, probability: 50% for each)data = bernoulli.rvs(size=1000, p=0.5)
ax = sns.distplot(data, kde=False, hist_kws={"linewidth":10, 'alpha':1})
ax.set(xlabel='Bernoulli', ylabel='Freq')# 横坐标,0或者1 纵坐标 频率次数
"""
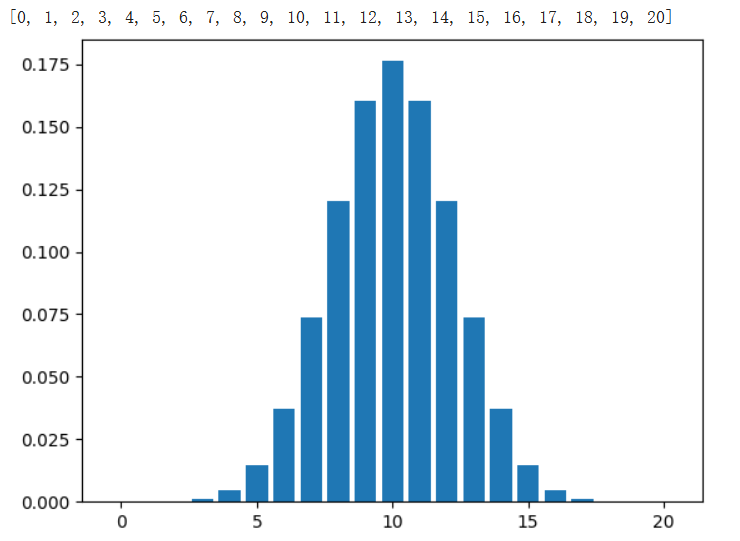
二项式分布伯努利分布是针对单个观测结果的。多个伯努利观测结果会产生二项式分布。例如,连续抛掷硬币。
试验是相互独立的。一个尝试的结果不会影响下一个。二项式分布可以表示为B(n, p)。 n 是试验次数, p 是成功的概率。p : 成功的概率 n : 实验次数 q=1-p : 失败的概率
"""import matplotlib.pyplot as plt
from scipy.stats import binomn = 20
# 实验的次数
p = 0.5
# 成功的概率
r = list(range(n + 1))
# print(r) #[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]
pmf_list = [binom.pmf(r_i, n , p) for r_i in r]
# 绘画
plt.bar(r, pmf_list)
plt.show()"""
该分布显示出成功结果数量增加的概率增加。
"""
"""
均匀分布
所有结果成功的概率相同。掷骰子,1 到 6。
次数越多,结果越接近均匀。
"""
import numpy as np
import seaborn as snsdata = np.random.uniform(1, 6, 1000)
ax = sns.distplot(data, kde=False, hist_kws={"linewidth":10, 'alpha':1})
ax.set(xlabel='Uniform', ylabel='Freq')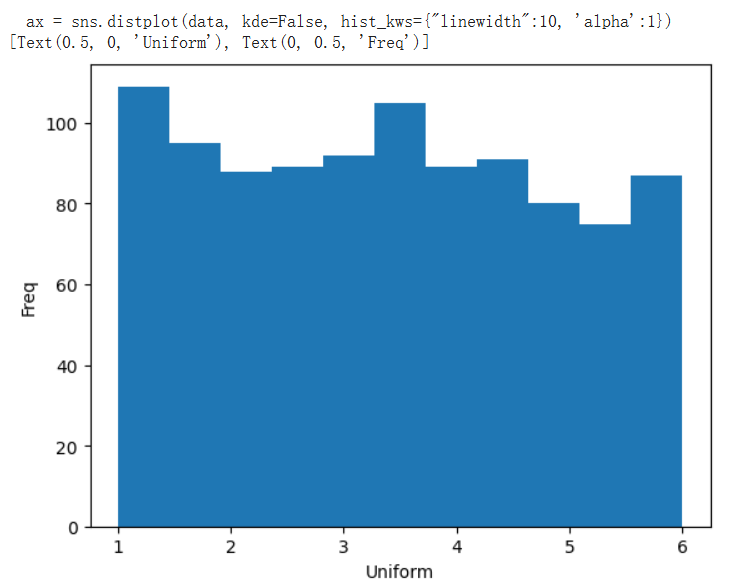
"""
poisson分布
它是与事件在给定时间间隔内发生频率相关的分布Po(λ) , λ是在指定时间间隔内预期发生的事件次数。它是在该时间间隔内发生的事件的已知平均值。X 是事件在指定时间间隔内发生的次数。如果事件遵循泊松分布,则:X ~ Po(λ)。在泊松分布中,事件彼此独立。事件可以发生任意次数。两个事件不能同时发生。如每 60 分钟接到 4 个电话。这意味着 60 分钟内通话的平均次数为 4。
让我们绘制在 60 分钟内接到 0 到 10 个电话的概率。
"""
!pip install poissonimport matplotlib.pyplot as plt
from scipy import stats
import poissonr = range(0, 11)
lambda_val = 4 # 呼叫次数
data = poisson.pmf(r, lambda_val) # 均值、 概率值
# 绘图
fig, sx = plt.subplots(1, 1, figsize=(10, 5))
ax.plot(r, data, 'bo', ms=8, label='poisson')
plt.ylabel("Probability", fontsize="12")
plt.xlabel("# Calls", fontsize="12")
plt.title("Poisson Distribution", fontsize="16")
ax.vlines(r, 0, data, colors='r', lw=5, alpha=0.5)"""
总结,概率图对,但是真实的电话次数,要根据 个人的历史数据 来算
"""
阿巴阿巴。。。。偷偷懒,不弄不弄,反正没人评论。。。。

如果你有历史数据(例如 N 小时内共收到 M 个电话),估计 λ 的方法很简单:
λ^=MN\hat{\lambda}=\frac{M}{N} \quadλ^=NM (单位: 每小时)
把估计的 λ 带入上面的代码,就得到基于历史的概率分布。
"""
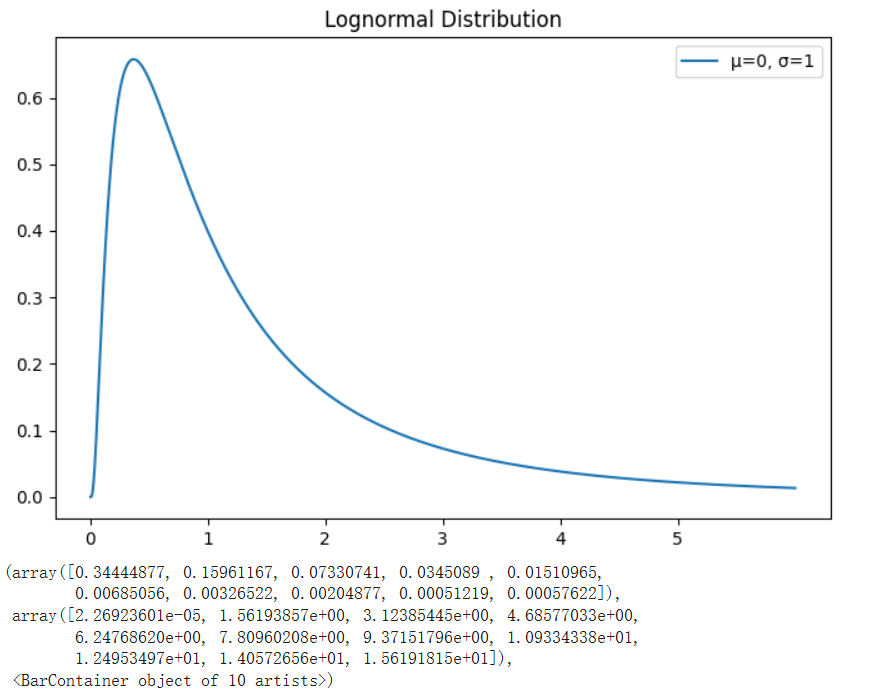
连续分布 ----正态、长尾、左偏、右偏、对数、指数分布对数正态分布
随机变量 X 的对数服从正态分布的分布。
"""import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
X = np.linspace(0, 6, 1500)
std = 1
mean = 0
lognorm_distribution = stats.lognorm([std], loc=mean)
lognorm_distribution_pdf = lognorm_distribution.pdf(X)
fig, ax = plt.subplots(figsize=(8, 5))
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=1")
ax.set_xticks(np.arange(min(X), max(X)))
plt.title("Lognormal Distribution")
plt.legend()
plt.show()
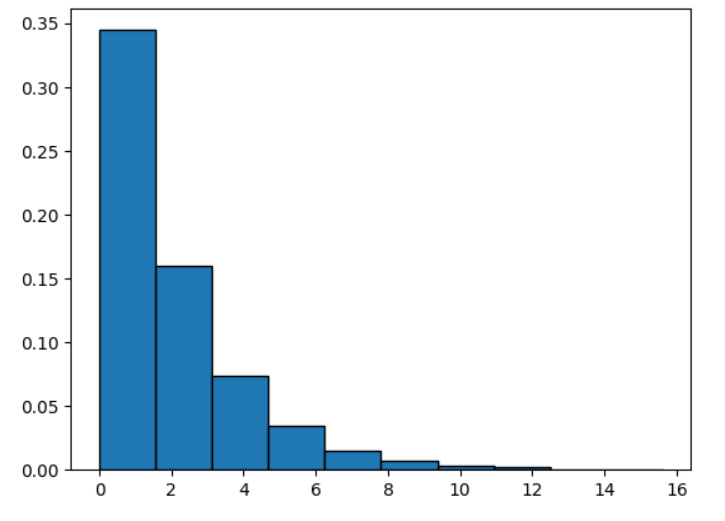
"""指数分布
我们在 Poisson 分布中研究了在一定时间间隔内发生的事件。在指数分布中,
我们关注的是两个事件之间经过的时间。如果我们把上面的例子倒过来,那么两个电话之间需要多长时间?
因此,如果 X 是一个随机变量,遵循指数分布,则累积分布函数为:
"""
from scipy.stats import expon
import matplotlib.pyplot as plt
x = expon.rvs(scale=2, size=10000)
# 绘图
plt.hist(x, density=True, edgecolor='black')
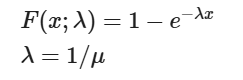
μ\muμ 是均值,eee 是常数。
总结
阿巴阿巴,今天阿巴日记又做了
致谢
靠咖啡续命的牛马,👍点赞 📁 关注 💬评论 💰打赏。
参考
[1] deepseek等ai
往期回顾
- 数据分析专栏记录之 -基础数学与统计知识:1、描述性统计
