齐次变换矩阵的逆变换:原理与SymPy实现
在机器人学、计算机图形学和三维视觉等领域,齐次变换矩阵是描述刚体运动的核心数学工具。它不仅能够表示旋转,还能同时表示平移,通过4×4矩阵的形式统一处理三维空间中的变换。本文将深入探讨齐次变换矩阵的逆变换原理,并展示如何使用SymPy符号计算库高效实现这一计算。
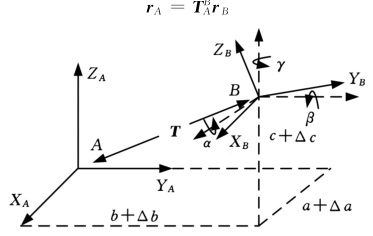
齐次变换矩阵的数学结构
齐次变换矩阵 TTT 的标准形式为:
T=[RP01] T = \begin{bmatrix} R & P \\ 0 & 1 \end{bmatrix} T=[R0P1]
其中 RRR 是一个3×3的旋转矩阵(满足正交性条件 RTR=IR^T R = IRTR=I),PPP 是一个3×1的平移向量,000 是1×3的零向量,右下角的 111 是标量。
这种表示法的优势在于能够将复杂的空间变换表示为单一的矩阵乘法操作,从而简化了坐标系之间的转换计算。
逆变换的数学原理
齐次变换矩阵的逆 T−1T^{-1}T−1 具有特殊的结构,可以直接通过公式计算:
T−1=[RT−RTP01] T^{-1} = \begin{bmatrix} R^T & -R^T P \\ 0 & 1 \end{bmatrix} T−1=[RT0−R
