算法第五十三天：图论part04（第十一章）

一.字符串接龙

思路整理

1. BFS建模

   • 这个题可以建模为 无权图最短路径问题。

   • 图的节点：每个单词。

   • 图的边：如果两个单词只有一个字母不同，则它们之间有一条边。

   • 问题变成：从 beginStr 出发，走最少几步到达 endStr。

2. BFS核心逻辑

   • 用队列 queue 维护搜索状态，每个状态包含：

     • 当前单词 word

     • 当前步数 step

   • 初始时入队 [beginStr, 1]（起点记为第1步）。

3. 搜索过程

   • 出队一个单词 word，判断是否已经到达 endStr：

     • 如果是，直接返回当前 step。

   • 否则，遍历 strList，找到所有与 word 相差一个字母的单词：

     • 若该单词未被访问过，则标记为已访问并入队 (nextWord, step+1)。

4. 终止条件

   • 若 BFS 队列空了仍未找到 endStr，说明无法转换，返回 0。

---

from collections import dequedef judge(s1, s2):count = 0for i in range(len(s1)):if s1[i] != s2[i]:count += 1return count == 1n = int(input())
beginStr, endStr = map(str, input().split())
if beginStr == endStr:print(0)exit() #直接结束整个程序
strList = []
for i in range(n):strList.append(input())visited = [False for _ in range(n)]
que = deque([[beginStr, 1]])        #[beginStr, 1]:外层 [] 是为了构造队列初始内容，内层 [] 是为了把 beginStr 和 1 绑在一起
while que:curStr, step = que.popleft()if judge(curStr, endStr):print(step+1)exit()for i in range(n):if not visited[i] and judge(strList[i], curStr):visited[i] = Trueque.append([strList[i], step+1])

二.有向图的完全可达性

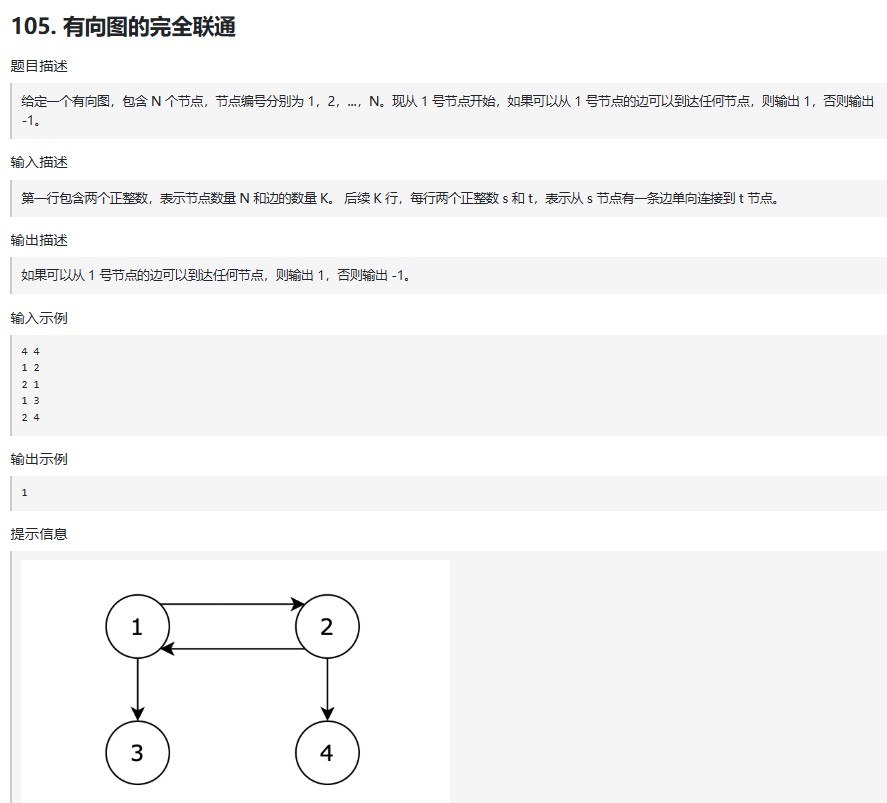
思路：

🚀 一、DFS（深度优先搜索）

思路：

• 核心思想：一条路走到黑，直到走不动再回溯。

• 递归 / 栈 实现。

• 用 visited（集合或数组）避免重复访问。

• 常用于：连通分量计数、拓扑排序、判断是否有环、路径搜索。

模板：

def dfs(node, graph, visited): if node in visited: return visited.add(node) # 遍历当前节点的所有邻居 for neighbor in graph[node]: dfs(neighbor, graph, visited)

---

🚀 二、BFS（广度优先搜索）

思路：

• 核心思想：按层扩展（逐层推进）。

• 队列 实现（collections.deque）。

• 也需要 visited 避免重复。

• 常用于：最短路径（无权图）、层序遍历。

模板：

from collections import deque def bfs(start, graph): visited = set([start]) queue = deque([start]) while queue: node = queue.popleft() for neighbor in graph[node]: if neighbor not in visited: visited.add(neighbor) queue.append(neighbor)

用bfs：

#有向图： 邻接表import collectionsdef bfs(root,graph):visited = set()que = collections.deque([root])visited.add(root)while que:cur = que.popleft()for nei in graph[cur]:if nei not in visited:visited.add(nei)que.append(nei)return visiteddef main():#读入 K 条边，构建一个 邻接表 graphN, K = map(int, input().split())graph = collections.defaultdict(list)for _ in range(K):src, dest = map(int, input().strip().split())graph[src].append(dest)visited = bfs(1, graph)if visited == set(range(1, N + 1)):return 1return -1if __name__ == "__main__":print(main())

用dfs

#有向图： 邻接表import collectionsdef dfs(node, graph, visited):if node in visited:returnvisited.add(node)for nei in graph[node]:dfs(nei, graph, visited)return visiteddef main():#读入 K 条边，构建一个 邻接表 graphN, K = map(int, input().split())graph = collections.defaultdict(list)for _ in range(K):src, dest = map(int, input().strip().split())graph[src].append(dest)visited = set()dfs(1, graph, visited)if visited == set(range(1, N + 1)):return 1return -1if __name__ == "__main__":print(main())