软件设计师——数据结构与算法基础学习笔记

一、数据结构与算法基础

数据结构与线性表

1. 下三角矩阵元素存储位置计算：

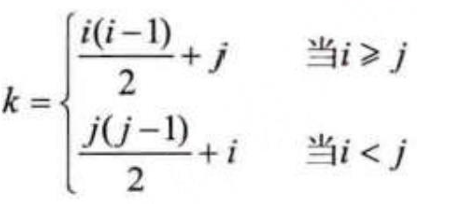
三对角矩阵是指除了主对角线及其相邻的两条对角线（上对角线和下对角线）外，其他位置的元素均为0的矩阵。
非零元素仅出现在以下位置：
主对角线 (i = j)：肯定有元素。
主对角线之上的一条对角线 (i = j - 1)：有元素。这条线也称为上对角线或上次对角线。
主对角线之下的一条对角线 (i = j + 1)：有元素。这条线也称为下对角线或下次对角线。
非零元素的总数为：

• 第一行：2个
• 中间 n−2n−2 行：每行3个 → 3×(n−2)
• 最后一行：2个

总计：3n−2
常用一维数组，按行优先存储，映射公式：k = 2i + j - 3

2. 队列的特性应用：

队列是一种遵循先进先出原则的线性数据结构，支持在队尾插入元素（入队）和队头删除元素（出队）。核心特性包括:
有序性：元素按插入顺序排列，先进入队列的元素优先被处理。
操作受限：仅允许在两端操作，不支持随机访问。
队列的典型应用场景: 任务调度与消息处理　广度优先搜索（BFS）　缓冲区管理　多线程同步 实时系统请求处理

3. 栈的特性应用：

栈是一种线性数据结构，遵循后进先出原则。最后压入栈的元素最先被弹出。栈的核心操作包括:
Push：将元素压入栈顶。
Pop：移除并返回栈顶元素。
Peek/Top：获取栈顶元素但不移除。
栈的典型应用场景： 函数调用与递归　表达式求值　括号匹配　浏览器历史记录　撤销操作

树

二叉树是一种树形数据结构，每个节点最多有两个子节点，通常称为左子节点和右子节点。

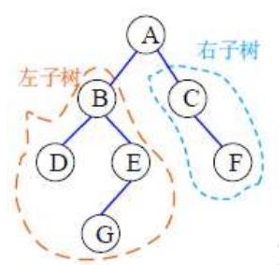
二叉树是许多高级数据结构（如二叉搜索树、堆、AVL树）的基础。
在树结构中，以下关系总是成立：
总结点数 = 叶子结点数 + 度为1的结点数 + 度为2的结点数 + … + 度为k的结点数。
总分支数（即树中所有结点的子节点总数） = 1 × 度为1的结点数 + 2 × 度为2的结点数 + … + k × 度为k的结点数。
在树中，总结点数 = 总分支数 + 1（因为根节点没有父节点，其他结点都有一个父节点）。

1. 二叉树的特性：

（1）在二叉树的第i层上最多有2ⁱ-1个结点（i≥1）。
（2）深度为k的二叉树最多有2^k-1个结点（k≥1）。
（3）对于任何一棵二叉树，如果其叶子结点数为n₀，度为2的结点数为n₂，则n₀=n₂+1。
（4）具有n个结点的完全二叉树的深度为[log₂n] +1。
（5）如果对一棵有n个结点的完全二叉树的结点按层序编号（从第1层到[log₂n]+1层，每层从左到右），则对任一结点i（1≤i≤n）有：
1）如果i=1，则该结点是二叉树的根，无双亲；如果i＞1，则该结点是i/2。
2）如果2i≤n，则该结点左子树的编号是2i；否则，无左子树。
3）如果2i+1≤n，则该结点右子树的编号是2i+1；否则，无右子树。

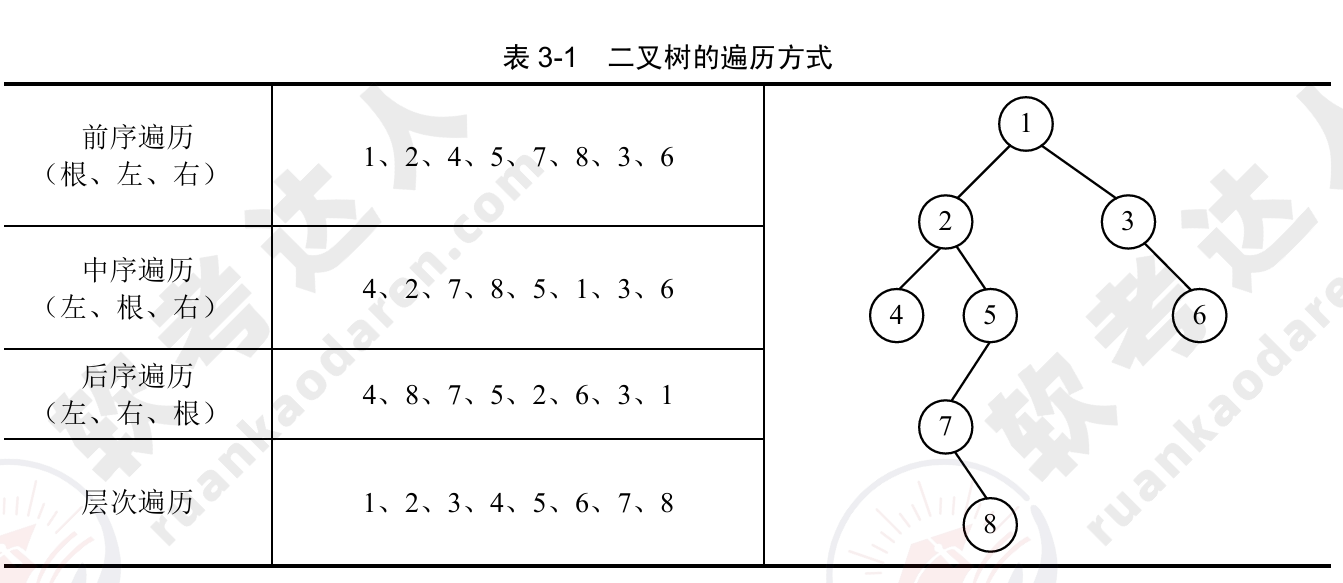
2.二叉树的遍历：

• 前序遍历（Pre-order）：访问根节点 → 遍历左子树 → 遍历右子树。
• 中序遍历（In-order）：遍历左子树 → 访问根节点 → 遍历右子树。
• 后序遍历（Post-order）：遍历左子树 → 遍历右子树 → 访问根节点。
• 层次遍历（Level-order）：按层从上到下访问节点，通常使用队列实现。

3. 特殊二叉树类型

完全二叉树：除最后一层外，其他层节点均填满，且最后一层节点靠左排列。常用于堆的实现。
满二叉树：所有非叶子节点都有两个子节点，且所有叶子节点在同一层。
二叉搜索树（BST）：左子树所有节点值小于根节点，右子树所有节点值大于根节点。中序遍历结果为有序序列。
平衡二叉树（AVL树）：任意节点的左右子树高度差不超过1，通过旋转操作保持平衡。

3.哈夫曼树(最优二叉树)：

哈夫曼树又称为最优二叉树，是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶子结点的权值乘上其到根结点的路径长度（若根结点为0层，叶子结点到根结点的路径长度为叶子结点的层数）。
其核心思想是通过频率或权重分配编码，高频（高权重）的字符使用较短的编码，低频字符使用较长的编码，从而实现整体编码长度最小化。
哈夫曼编码的生成
从根节点出发，向左子树路径标记为 0，向右子树路径标记为 1。每个叶子节点的路径编码即为对应字符的哈夫曼编码。

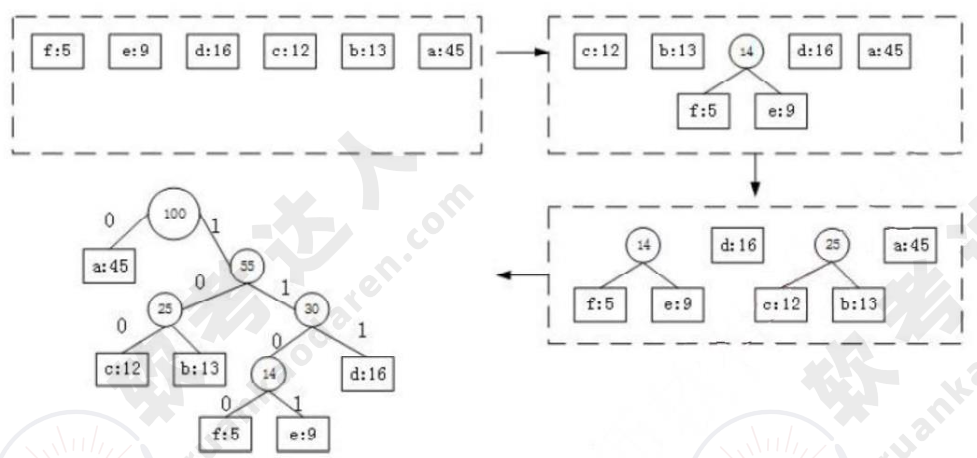
压缩比=（定长-变长）/定长

图

1.图的存储结构：

（1）邻接矩阵。邻接矩阵表示法是指用一个矩阵来表示图中顶点之间的关系。对于具有n个
顶点的图G=(V,E)，其邻接矩阵是一个n阶方阵且满足：


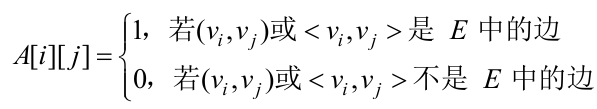
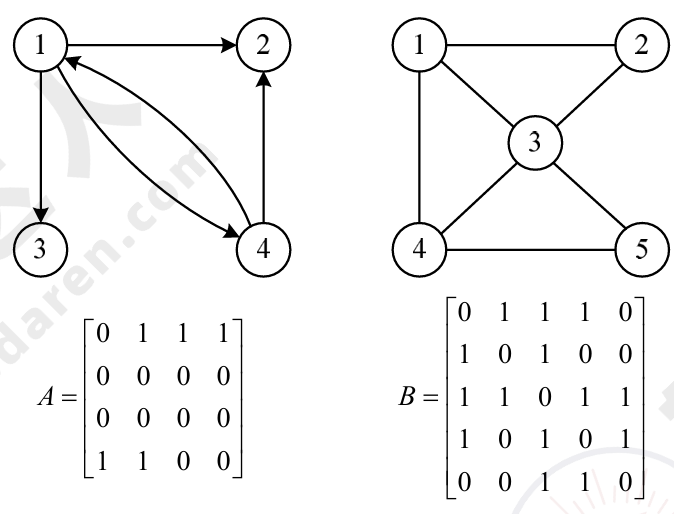
无向图的邻接矩阵是对称的，有向图的邻接矩阵则不一定对称。完全有向图的邻接矩阵也对称。
（2）邻接表。邻接表表示法是指为图中的每一个顶点建立一个单链表。

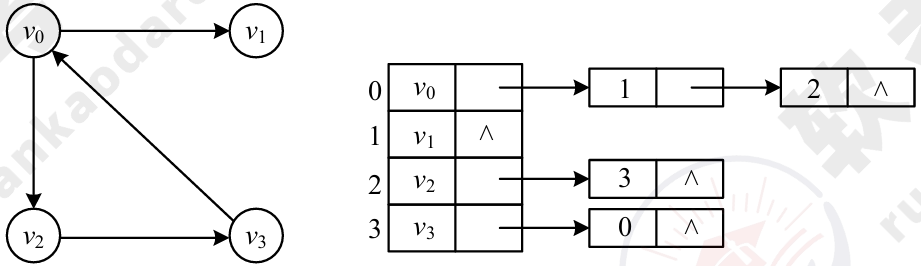
存储特点： 图中的顶点数决定了邻接矩阵的阶和邻接表中的单链表数目，无论是对有向图还是无向图，边数的多少决定了单链表中的结点数，而不影响邻接矩阵的规模，因此采用何种存储方式与有向图、无向图没有区别，要看图的边数和顶点数，完全图适合采用邻接矩阵存储。

查找与排序

1．顺序查找

将待查的元素从头到尾与表中元素进行比较，如果存在，则返回成功；否则，查找失败。此方法效率不高。顺序查找的平均查找长度为(n+1)/2。
顺序查找的方法对于顺序存储方式和链式存储方式的查找表都适用。

2．二分查找 （折半查找）

二分查找的前提是元素有序（一般是升序），基本思路是拿中间元素A[m]与要查找的元素x进行比较，如果相等，则表示找到；如果A[m]比x大，那么要找的元素一定在A[m]前边（左边）；如果A[m]比x小，那么要找的元素一定在A[m]后边（右边）。每进行一次查找，数组规模减半。反复将子数组规模减半或使当前子数组为空，直到发现要查找的元素。

无论查找成功与否，折半查找的最大关键字比较次数均为： $$\lfloor {\log }_{2}n\rfloor +1$$

折半查找（二分查找）在有序数组中的时间复杂度为 O(log₂n)

3．哈希查找

设关键序列为47、34、13、12、52、38、33、27、3，哈希表长为11，哈希函数为Hash(key)=key
mod 11，则有：
Hash(47) = 47 mod 11= 3，Hash(34) = 34 mod 11= 1，Hash(13) =13 mod 11= 2，
Hash(12) = 12 mod 11= 4，Hash(52) = 52 mod 11= 8，Hash(38) = 38 mod 11= 5，
Hash(33) = 33 mod 11= 0，Hash(27) = 27 mod 11= 6，Hash(3) =3 mod 11= 7。
对于产生的冲突，哈希函数可以采用线性探测法解决冲突，哈希地址和关键字的对应关系如表所示。

4. 排序

5. 直接插入排序

在插入第i个记录时，R1,R2,…,Ri-1均已排好序，这时将第i个记录依次与Ri-1,…,R2,R1进行比较，找到合适的位置插入，插入位置及之后的记录依次向后移动。

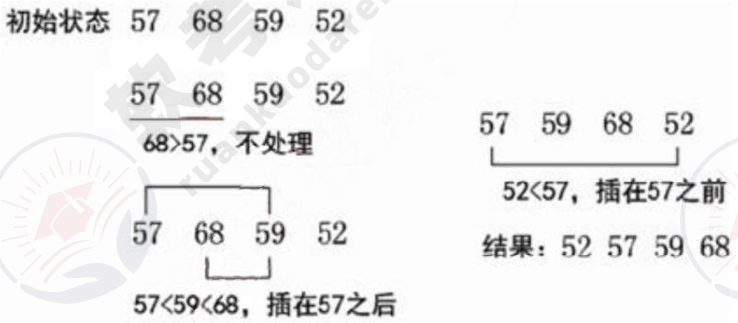
直接插入排序在最好情况下的时间复杂度为O(n)，在最坏情况下的时间复杂度为O(n²)。

6．冒泡排序

通过相邻元素（i 与 i-1）之间的比较和交换，将排序码较小的元素逐渐从底层移向顶层。整个过程像水底的气泡逐渐向上冒，由此而得名冒泡排序。冒泡排序的时间复杂度为O(n²)。

7．简单选择排序

每一趟从待排序的数据元素中选出最小的元素，顺序放在待排序数列的最前面，直到全部待排
序的数据元素全部排完。简单选择排序的时间复杂度为O(n²)。

8．快速排序

快速排序是对冒泡排序的一种改进。基本思路是：通过一趟排序将要排序的数据分成独立的两个部分，其中一部分的所有数据都比另外一部分的所有数据要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

快速排序在最好情况下的时间复杂度为O(nlog₂n)；在最坏情况下，即初始序列按关键字有序或基本有序时，快速排序的时间复杂度为O(n²)。

9．堆排序

对于n个元素的序列，当且仅当满足下列关系时称其为堆，其中，2i 和 2i+1不大于n。

其中，前者称为小顶堆，后者称为大顶堆。
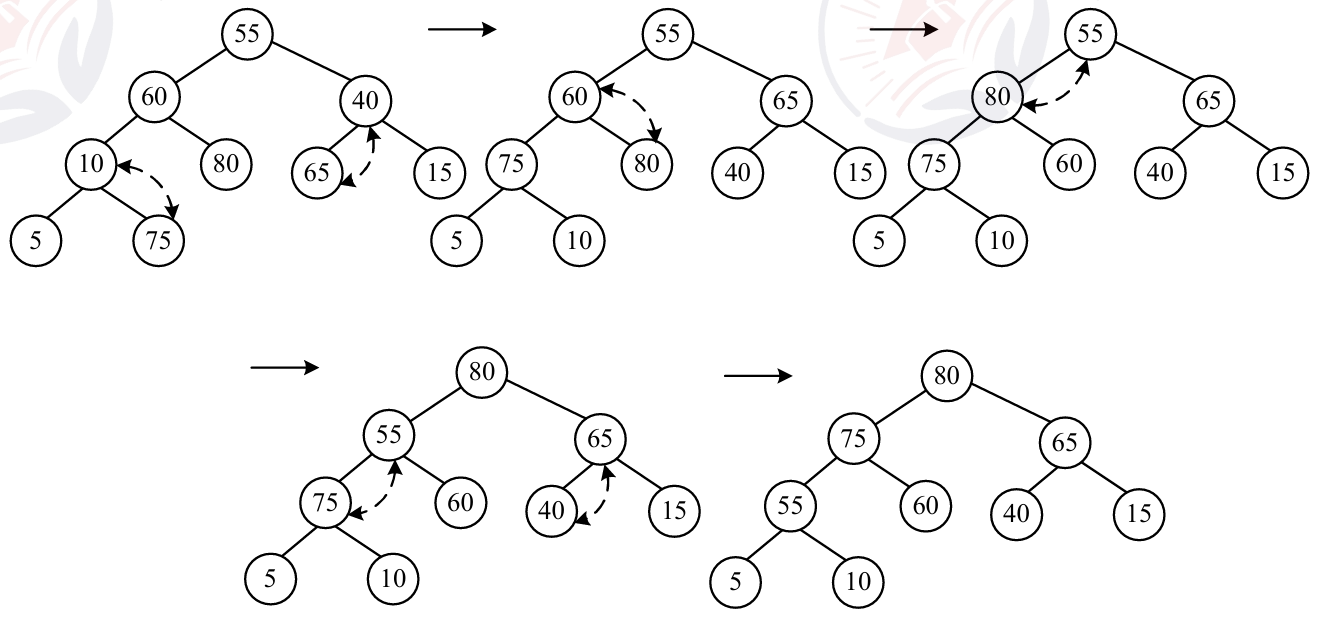
堆排序的基本思路是：对于一组待排序记录的关键字，首先按堆的定义排成一个序列（建立初始堆），之后输出堆顶最大关键字（对于大顶堆而言），然后将剩余的关键字再调整成新堆，从而得到次大关键字，如此反复，直到全部关键字排成有序序列为止。堆排序（以大顶堆为例）的建立过程与调整新堆的过程如图所示。堆排序的时间复杂度为O(nlog₂n)。

10．归并排序

所谓“归并”，是将两个或两个以上的有序文件合并成为一个新的有序文。归并排序过程分为三步：
（1）分解。将n个元素分成各含n/2个元素的子序列。
（2）求解。用归并排序对两个子序列递归地排序。
（3）合并。合并两个已经排好序的子序列以得到排序结果。

归并排序的时间复杂度为O(nlog₂n)。
以下是符合Markdown格式的排序算法对比表格：

11. 排序算法对比

排序算法	平均时间复杂度	最坏时间复杂度	最好时间复杂度	空间复杂度	稳定性	适用场景
冒泡排序	O(n²)	O(n²)	O(n)	O(1)	稳定	小规模数据或基本有序
选择排序	O(n²)	O(n²)	O(n²)	O(1)	不稳定	小规模数据
插入排序	O(n²)	O(n²)	O(n)	O(1)	稳定	小规模或部分有序数据
希尔排序	O(n log n)	O(n²)	O(n log n)	O(1)	不稳定	中等规模数据
归并排序	O(n log n)	O(n log n)	O(n log n)	O(n)	稳定	大规模数据，需额外空间
快速排序	O(n log n)	O(n²)	O(n log n)	O(log n)	不稳定	大规模数据，通用场景
堆排序	O(n log n)	O(n log n)	O(n log n)	O(1)	不稳定	大规模数据，无需额外空间
计数排序	O(n + k)	O(n + k)	O(n + k)	O(k)	稳定	非负整数，范围较小
基数排序	O(n × k)	O(n × k)	O(n × k)	O(n + k)	稳定	非负整数，位数较少

算法基础知识

1. 时间复杂度分析

主定理的核心思想

主定理（Master Theorem）提供了一种快速求解分治算法递归式的方法，特别适用于形式如 $T(n)=aT(n/b)+f(n)$ 的递归关系，其中：

• $a$ 是子问题的数量；
• $n/b$ 是每个子问题的规模；
• $f(n)$ 是合并子问题结果的开销。

主定理的三种情况

情况一：叶子层开销主导
如果 $f(n)$ 的增长速度慢于 $n^{{\log }_{b}a}$，即 $f(n)=O(n^{{\log }_{b}a-ϵ})$（$ϵ>0$），则递归的解由叶子层的操作决定：
$$T(n)=\Theta (n^{{\log }_{b}a})$$

情况二：各层开销平衡
如果 $f(n)$ 和 $n^{{\log }_{b}a}$ 同阶，即 $f(n)=\Theta (n^{{\log }_{b}a}{\log }^{k}n)$（$k\ge 0$），则解为：
$$T(n)=\Theta (n^{{\log }_{b}a}{\log }^{k+1}n)$$
常见的是 $k=0$，此时 $T(n)=\Theta (n^{{\log }_{b}a}\log n)$。

情况三：合并开销主导
如果 $f(n)$ 增长快于 $n^{{\log }_{b}a}$，即 $f(n)=\Omega (n^{{\log }_{b}a+ϵ})$（$ϵ>0$），且满足正则条件 $af(n/b)\le cf(n)$（$c<1$），则解由合并操作决定：
$$T(n)=\Theta (f(n))$$

直观理解

• 情况一：递归树的叶子节点（最底层）操作数量最多，总时间由叶子层决定。
• 情况二：每一层的操作数量相近，总时间是层数×每层时间。
• 情况三：根节点（合并步骤）的开销最大，总时间由合并步骤主导。

经典例子

1. 二分查找：$T(n)=T(n/2)+\Theta (1)$
   属于情况二，$a=1,b=2$，$f(n)=\Theta (1)$，$n^{{\log }_{b}a}=1$，故 $T(n)=\Theta (\log n)$。

2. 归并排序：$T(n)=2T(n/2)+\Theta (n)$
   属于情况二，$a=2,b=2$，$f(n)=\Theta (n)$，$n^{{\log }_{b}a}=n$，故 $T(n)=\Theta (n\log n)$。

3. 快速排序（平均情况）：$T(n)=2T(n/2)+\Theta (n)$
   与归并排序相同，解为 $\Theta (n\log n)$。