当前位置： 首页 > news >正文

常见的排序算法

news 2025/8/19 11:36:49

快速排序：

核心思路1：分俩块区域

//[left,pivotIndex - 1],[pivotIndex + 1 ,right]
  1. 选择基准值（pivot）：从数组中选一个元素作为基准（通常选第一个、最后一个或中间元素）。
  2. 分区（partition）：将数组划分为两部分，左半部分元素都小于基准值，右半部分元素都大于基准值（基准值最终位于两部分之间的正确位置）。
  3. 递归排序：对左右两部分分别重复上述步骤，直至子数组长度为 1（天然有序）。
package demo;import java.util.Arrays;public class MyQuickSort {public static void main(String[] args) {int[] arr = {1,0,10,16,-1,5,-18};quickSort(arr,0,arr.length-1);//threeQuickSort(arr,0,arr.length-1);System.out.println(Arrays.toString(arr));}private static void quickSort(int[] arr, int left, int right) {//递归出口if(left >= right){return;}//先进行分区int pivotIndex = partition(arr,left,right);//[left,pivotIndex - 1],[pivotIndex + 1 ,right] 递归调用quickSort(arr,left,pivotIndex-1);quickSort(arr,pivotIndex+1,right);}private static int partition(int[] arr, int left, int right) {//确定一个基准int pivot = arr[left];int i = left , j = right;while(i < j) {//在右边找到第一个比pivot小的数while (i < j && arr[j] >= pivot ) {j--;}//在左边找到第一个比pivot大的数while(i < j && arr[i] <= pivot) {i++;}//如果找到了if(i < j) {swap(arr,i,j);}}//最终将 i/j 和 left 交换swap(arr,i,left);return i;}private static void swap(int[] arr, int l , int r) {int temp = arr[l];arr[l] = arr[r];arr[r] = temp;}}

核心思路2：分三块区域

[left,lt - 1] , [lt, gt] , [gt+1 , right]
一、为什么需要三分快排？

传统快速排序在处理包含大量重复元素的数组时效率较低。例如，当数组中多数元素相同时，传统快排会将数组划分为 “小于基准” 和 “大于基准” 两部分，但重复元素会被多次处理，导致时间复杂度退化至 O (n²)。

选择一个基准值 x，通过一次遍历将数组分割为三个连续区间：

  • 左区间：所有元素 < x
  • 中间区间：所有元素 = x
  • 右区间：所有元素 > x

之后，仅对左区间（<x）和右区间（>x）递归排序，中间区间（=x）已处于最终位置，无需再处理。

package demo;import java.util.Arrays;public class MyQuickSort {public static void main(String[] args) {int[] arr = {1,0,10,16,-1,5,-18};//quickSort(arr,0,arr.length-1);threeQuickSort(arr,0,arr.length-1);System.out.println(Arrays.toString(arr));}private static void threeQuickSort(int[] arr , int left , int right) {//递归出口if(left >= right){return;}//定义一个基准int pivot = arr[left];int lt = left ,gt = right  ;int i = left + 1;while (i <= gt) {//应该放右边if(arr[i] > pivot) {swap(arr,i,gt--);}else if(arr[i] < pivot) {swap(arr,i++,lt++);}else {i++;}}//[left,lt - 1] , [lt, gt] , [gt+1 , right]//继续递归threeQuickSort(arr,left,lt-1);threeQuickSort(arr,gt+1,right);}private static void swap(int[] arr, int l , int r) {int temp = arr[l];arr[l] = arr[r];arr[r] = temp;}}

堆排序：

核心思路

  • 把数组 “变成” 大顶堆（父节点 ≥ 子节点），此时堆顶（数组第一个元素）是最大值。
  • 把最大值放到数组末尾（通过交换堆顶和末尾元素），相当于 “提取” 最大值并固定。
  • 把剩余元素重新 “变回” 大顶堆，重复步骤 2，直到所有元素都被固定。
package demo;import java.util.Arrays;public class MyHeapSort {public static void main(String[] args) {int[] arr = {1,0,10,16,-1,5,-18};heapSort(arr,0,arr.length-1);System.out.println(Arrays.toString(arr));}private static void heapSort(int[] arr, int left , int right) {// 边界条件：空数组或只有一个元素无需排序if (arr == null || arr.length <= 1) {return;}int n = arr.length;//构建大根堆for(int i = n / 2 -1; i >= 0; i--) {heapify(arr,n,i);}// 第二步：逐步提取最大值并调整堆for (int i = n - 1; i > 0; i--) {// 交换堆顶（最大值）和当前末尾元素swap(arr, 0, i);// 对剩余元素重新调整为大顶堆，堆大小减1heapify(arr, i, 0);}}private static void heapify(int[] arr, int heapSize, int i) {// 初始化最大值位置为当前节点int largest = i;//计算左右节点的索引int leftChild = 2 * i + 1 , rightChild = 2 * i + 2;if(leftChild < heapSize && arr[leftChild] > arr[largest]) {largest = leftChild;}if(rightChild < heapSize && arr[rightChild] > arr[largest]) {largest = rightChild;}if(largest != i) {swap(arr,largest,i);// 递归调整受影响的子树heapify(arr, heapSize, largest);}}private static void swap(int[] arr, int l , int r) {int temp = arr[l];arr[l] = arr[r];arr[r] = temp;}}

归并排序

核心思路

将复杂问题拆解为更小的子问题，解决子问题后再将结果合并，最终得到整体解。对于排序而言：

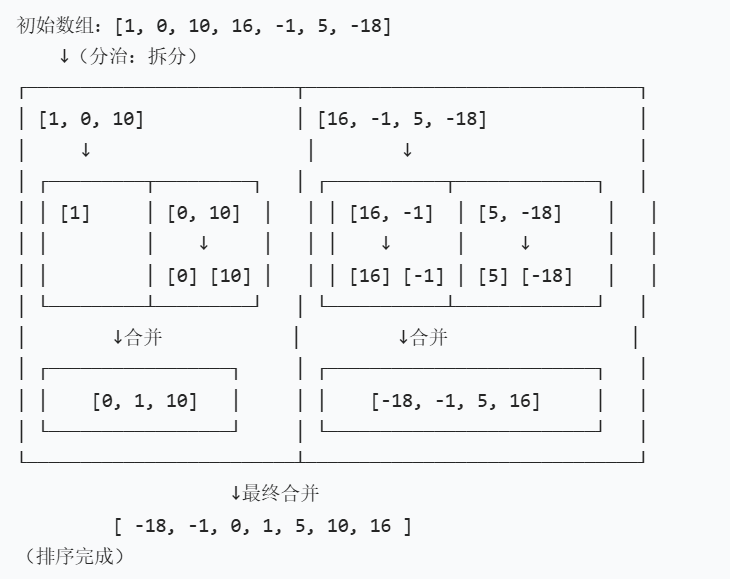
  • 分：将大数组不断二分，直到每个子数组只包含 1 个元素（单个元素天然有序）。
  • 治：将两个已排序的子数组合并为一个更大的有序数组。
  • 递归：通过递归重复 “分” 和 “治”，直至整个数组有序。
package demo;import java.util.Arrays;public class MyMergeSort {static int[] res;public static void main(String[] args) {int[] arr = {1,0,10,16,-1,5,-18};res = new int[arr.length];mergeSort(arr,0,arr.length-1);System.out.println(Arrays.toString(arr));}private static void mergeSort(int[] arr, int left, int right) {//只有1个元素if(left >= right) {return;}//拿到中间值int mid = left + (right - left) / 2;//递归mergeSort(arr, left, mid);mergeSort(arr, mid+1, right);//合并int k = 0;int i = left , j = mid+1;while (i <= mid && j <= right) {res[k++] = arr[i] <= arr[j] ? arr[i++] : arr[j++];}//处理边界情况while (i <= mid) {res[k++] = arr[i++];}while (j <= right) {res[k++] = arr[j++];}//填回值for(int n = left; n <= right; n++) {arr[n] = res[n - left];}}
}

  • 快速排序：
    适合中等规模至大规模的数组排序，尤其是对排序速度要求高且可接受不稳定排序的场景（如编程语言内置排序函数、日常业务数据排序）。

  • 堆排序：
    适合内存紧张的场景（如嵌入式系统）、需要实时维护最大 / 最小值的场景（如优先级队列、Top K 问题），或对时间复杂度稳定性要求极高的场景。

  • 归并排序：
    适合需要稳定排序的场景（如多字段排序）、链表排序、外部排序（大数据），或对排序稳定性要求严格的业务（如数据库查询结果排序）。

冒泡排序

核心思想：重复比较相邻元素，将大的元素逐步 "冒泡" 到末尾。

public class MyBubbleSort {public static void main(String[] args) {int[] arr = {1,0,10,16,-1,5,-18};bubbleSort(arr);System.out.println(Arrays.toString(arr));}private static void bubbleSort(int[] arr) {if (arr == null || arr.length <= 1) return;//外层次数for(int i = 0 ; i < arr.length - 1 ; i++) {boolean flag = false;//内层循环比较相邻元素for(int j = 0; j < arr.length - 1 - i; j++) {//前一个元素大于后面一个if(arr[j] > arr[j + 1] ) {swap(arr,j,j+1);flag = true;}}//已经有序 直接退出if(!flag) break;}}private static void swap(int[] arr, int l , int r) {int temp = arr[l];arr[l] = arr[r];arr[r] = temp;}}

选择排序

核心思想：每次从剩余元素中找到最小（大）值，放到已排序序列的末尾。

public class MySelectionSort {public static void main(String[] args) {int[] arr = {1,0,10,16,-1,5,-18};SelectionSort(arr);//threeQuickSort(arr,0,arr.length-1);System.out.println(Arrays.toString(arr));}private static void SelectionSort(int[] arr) {if(arr == null || arr.length <= 1 ) return;for(int i = 0 ; i < arr.length - 1 ; i++) {//固定第一个值int minIndex = i;for(int j = i + 1; j < arr.length ;j++) {if(arr[j] < arr[minIndex]) {minIndex = j;}}//找到最小值交换到第一个元素swap(arr,i,minIndex);}}private static void swap(int[] arr, int l , int r) {int temp = arr[l];arr[l] = arr[r];arr[r] = temp;}
}

插入排序

核心思想：将元素逐个插入到已排序的序列中，类似整理扑克牌。

public class MyInsertSort {public static void main(String[] args) {int[] arr = {1,0,10,16,-1,5,-18};insertSort(arr);System.out.println(Arrays.toString(arr));}private static void insertSort(int[] arr) {if(arr == null || arr.length <= 1 ) return;//从第二个元素开始插，默认第一个有序for(int i = 1 ; i < arr.length ; i++) {//保存待插入元素int tmp = arr[i];int j = i -1;//从后往前比较，找到待插入元素的位置while(j >= 0 && arr[j] >tmp) {//向后移arr[j + 1] = arr[j];j--;}//插入待插入元素到正确位置arr[j + 1] = tmp;}}
}

希尔排序

核心思想：对插入排序的优化，通过分组（步长）减少元素移动次数，逐步缩小步长至 1。

public class MyShellSort {public static void main(String[] args) {int[] arr = {1,0,10,16,-1,5,-18};shellSort(arr);System.out.println(Arrays.toString(arr));}private static void shellSort(int[] arr) {if(arr == null || arr.length <= 1) return;int n = arr.length;// 初始化步长（通常为数组长度的一半，逐步减半）for(int gap = n / 2 ; gap > 0 ; gap/=2) {for(int i = gap ; i < n;i++) {// 对每个分组执行插入排序   int tmp = arr[i];int j = i - gap;while (j >= 0 && arr[j] > tmp) {arr[j + gap] = arr[j];j-= gap;}arr[j + gap] = tmp;}}}
}

http://www.dtcms.com/a/338122.html

相关文章：

  • 【PZ-ZU47DR-KFB】璞致FPGA ZYNQ UltraScalePlus RFSOC QSPI Flash 固化常见问题说明
  • 免费又强大的 PDF 编辑器 ——PDF XChange Editor
  • c++之static和const
  • Python实战--基于Django的企业资源管理系统
  • 基于KubeSphere的Kubernetes生产实践之路-起步篇
  • K8s部署java程序
  • 数据清洗（Data Cleansing）新手教学简单易懂（缺失值、异常值、重复数据、不一致数据、格式问题），附实战案例
  • php8.+ 新函数总结
  • 了解Arthas-7788
  • GO学习记录六——集成Swagger接口测试页面
  • Three.js 坐标系系统与单位理解教程
  • 安装pnpm i -D @types/wechat-miniprogram报错，版本不匹配
  • 使用 Zed + Qwen Code 搭建轻量化 AI 编程 IDE
  • 【CF】Day129——杂题 (状压DP + 图论 | 贪心 + 数论 + 构造 | 构造 + 贪心 | 构造 + 模拟)
  • Python装饰器：从入门到精通
  • 【STM32】SPI 与 Flash 笔记
  • 【深度长文】Anthropic发布Prompt Engineering全新指南
  • 启发式合并
  • 1、代码相关优化建议
  • 数据分析进阶——解读文本分析模型【附全文阅读】
  • 第十六届蓝桥杯青少组C++省赛[2025.8.10]第二部分编程题（5、环形取硬币游戏）
  • 虚幻基础：动作时间窗
  • Kafka文件存储机制
  • 录音转文字，如何做到“快、准、狠“多格式通吃？
  • 自学中医笔记（二）
  • 大模型对齐算法(四): DAPO,VAPO,GMPO,GSPO, CISPO，GFPO
  • 如何平衡电竞酒店和高校宿舍对AI云电竞游戏盒子的不同需求？
  • 【Python】Python 多进程与多线程：从原理到实践
  • NVIDIA CWE 2025 上海直击：从 GPU 集群到 NeMo 2.0，企业 AI 智能化的加速引擎
  • 软件定义汽车---创新与差异化之路