当前位置： 首页 > news >正文

数据结构——线性表

news 2025/8/18 16:28:15

一、引入

顺序表、单向链表、单向循环链表、双向链表、双向循环链表、顺序栈、链式栈、循环队列（顺序队列）、链式队列

1）逻辑结构：线性结构

2）存储结构：顺序、链式

3）特点：一对一，每一个节点最多有一个前驱和一个后继，首节点无前驱，尾节点无后继

函数名命名规则：

下滑线法：create_empty_seqlist

小驼峰法：createEmptySeqList

大驼峰法：CreateEmptySeqList

二、顺序表

1、特点和三要素

特点：内存连续（数组）

1）逻辑结构：线性结构

2）存储结构：顺序存储

3）操作：增删改查

2、数组的插入和删除操作

假设定义了数组：int a[100] = {1, 2, 3, 4, 5, 6, 7, 8};

2.1 插入操作

向数组的第几个位置插入数据，如下图

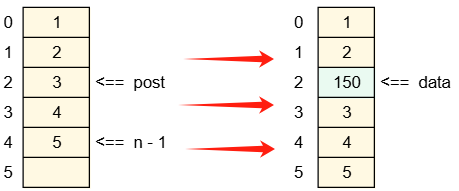
实现函数功能需要传参，分别有以下参数：

int *p; // 保存的数组的首地址

int n; // n代表的是数组中有效的元素个数（非数组的长度size 100）

int post; // 在下标为post处插入数据

int data; // 插入到数组中的数据

void insertIntoA(int * p, int post, int data, int n)

{

        // 1.将n-1位置到post位置的数据整体向后移动一位

        // 2.将data赋值到post位置

}

// 参数1：数组首地址
// 参数2：指定的下标位置
// 参数3：插入的数据
// 参数4：元素总个数
void insertIntoA(int *p, int post, int data, int n)
{
    for (int i = n - 1; i >= post; i--)
        // p[i + 1] = p[i];                 /*方法一*/// *(p + i + 1) = *(p + i);       /*方法二*/
    p[post] = data;
}

2.2 删除操作

删除数组指定位置的数据，如下图

// 参数1：数组首地址
// 参数2：指定的下标位置
// 参数3：元素总个数
void deleteFromA(int *p, int post, int n)
{
    for (int i = post + 1; i <= n - 1; i++)
        // p[i - 1] = p[i];                 /*方法一*/// *(p + i - 1) = *(p + i);       /*方法二*/
}

2.3 初版删除插入操作

#include<stdio.h>
/*==========向数组指定位置处插入指定数据==========*/
void insertIntoA(int *p, int post, int data, int n)
{
    for (int i = n - 1; i >= post; i--)
        // p[i + 1] = p[i];         /*方法一*/
        *(p + i + 1) = *(p + i);    /*方法二*/
    p[post] = data;
}
/*============删除数组指定位置数据==============*/
void deleteFromA(int *p, int post, int n)
{
    for (int i = post + 1; i < n; i++)
        // p[i - 1] = p[i];         /*方法一*/
        *(p + i - 1) = *(p + i);
}
/*=================循环遍历数组=================*/
void showA(int *p, int n)
{
    for (int i = 0; i < n; i++)
        printf("%d ", p[i]);
    putchar(10);
}
/*====================主函数====================*/
int main(int argc, char const *argv[])
{
    int a[100] = {1, 2, 3, 4, 5, 6, 7, 8};
    insertIntoA(a, 3, 400, 8);  // 1 2 3 400 4 5 6 7 8
    showA(a, 9);
    deleteFromA(a, 3, 9);   // 1 2 3 4 5 6 7 8
    showA(a, 8);
    return 0;
}

3、修改为last版本

#include<stdio.h>
int last = 7;   // 最后一个有效元素的下标/*==========向数组指定位置处插入指定数据==========*/
// 参数1：数组首地址
// 参数2：指定位置
// 参数3：插入数据
void insertIntoA(int *p, int post, int data)
{
    for (int i = last; i >= post; i--)
        // p[i + 1] = p[i];         /*方法一*/
        *(p + i + 1) = *(p + i);    /*方法二*/
    p[post] = data;
    last++;     // 有效数据元素下标+1
}/*==============删除数组指定位置数据==============*/
// 参数1：数组首地址
// 参数2：指定位置
void deleteFromA(int *p, int post)
{
    for (int i = post + 1; i <= last; i++)
        // p[i - 1] = p[i];         /*方法一*/
        *(p + i - 1) = *(p + i);
    last--;     // 有效数据元素下标-1
}/*================遍历输出数组================*/
// 参数1：数组首地址
void Printf(int *p)
{
    for (int i = 0; i < last + 1; i++)
        printf("%d ", p[i]);
    putchar(10);
}/*====================主函数====================*/
int main(int argc, char const *argv[])
{
    int a[100] = {1, 2, 3, 4, 5, 6, 7, 8};  // 定义数组
    Printf(a);
    insertIntoA(a, 3, 400);     // 下标3，插入400
    Printf(a);
    deleteFromA(a, 3);          // 下标3，删除
    Printf(a);
    return 0;
}

4、顺序表相关操作

结构体：​​​​​​​

#define N 5

typedef struct seq

{

        int data[N];

        int last;

} seqlist_t;

头文件：

#ifndef _SEQLIST_H__
#define _SEQLIST_H__
#include <stdio.h>
#include <stdlib.h>
#define N 5
typedef struct seq
{
    int data[N];
    int last;
}seqlist_t;
//1.创建一个空的顺序表
seqlist_t *CreateEpSeqlist();//返回的是申请空间的首地址
//2.向顺序表的指定位置插入数据
int InsertIntoSeqlist(seqlist_t *p, int post,int data);//post第几个位置，data插入的数据
//3.遍历顺序表sequence 顺序 list 表
void ShowSeqlist(seqlist_t *p);
//4.判断顺序表是否为满,满返回１ 未满返回０
int IsFullSeqlist(seqlist_t *p);
//5.判断顺序表是否为空
int IsEpSeqlist(seqlist_t *p);
//6.删除顺序表中指定位置的数据post删除位置
int DeletePostSeqlist(seqlist_t *p, int post);
//7.清空顺序表
void ClearSeqList(seqlist_t *p);
//8.修改指定位置的数据
int ChangePostSeqList(seqlist_t *p,int post,int data);//post被修改的位置，data修改成的数据
//9.查找指定数据出现的位置
int SearchDataSeqList(seqlist_t *p,int data);//data代表被查找的数据
#endif

最终版

fun.c中代码：

#include "seqlist.h"
/*=======================1、创建一个空的顺序表=======================*/
seqlist_t *CreateEpSeqlist() // 返回的是申请空间的首地址
{
    // 1.开辟一个结构体大小的空间
    seqlist_t *p = (seqlist_t *)malloc(sizeof(seqlist_t));
    if (p == NULL)
    {
        perror("malloc err"); // 可以返回错误缘由
        return NULL;
    }
    // 2.对last初始化
    p->last = -1; // 代表数组为空
    return p;
}
/*===============4.判断顺序表是否为满,满返回１ 未满返回０==============*/
int IsFullSeqlist(seqlist_t *p)
{
    return p->last + 1 == N; // 相等则满返回1，不等则不满返回0
}/*====================2、向顺序表的指定位置插入数据====================*/
int InsertIntoSeqlist(seqlist_t *p, int post, int data) // post第几个位置，data插入的数据
{
    // 0.容错判断
    if (IsFullSeqlist(p) || post < 0 || post > p->last + 1)
    {
        perror("InsertIntoSeqlist error");
        return -1;
    }
    // 1.将last到post位置所有数据整体向后移动一个位置
    for (int i = p->last; i >= post; i--)
        p->data[i + 1] = p->data[i];
    // 2.将data数据插入post位置
    p->data[post] = data;
    // 3.最后一个有效元素下标+1
    p->last++;
    return 0;
}/*========================5、判断顺序表是否为空========================*/
int IsEpSeqlist(seqlist_t *p)
{
    return p->last == -1;
}/*====================6、删除顺序表中指定位置的数据post删除位置====================*/
int DeletePostSeqlist(seqlist_t *p, int post)
{
    // 0.容错判断
    if (IsEpSeqlist(p) || post < 0 || post > p->last)
    {
        perror("DeletePostSeqlist error");
        return -1;  // 返回值是int类型，所以错误返回-1
    }
    // 1.将last到post + 1位置所有数据整体向前移动一个位置
    for (int i = post + 1; i <= p->last; i++)
        p->data[i - 1] = p->data[i];
    // 2.最后一个有效元素下标-1
    p->last--;
    return 0;
}
/*====================3、遍历顺序表====================*/
void ShowSeqlist(seqlist_t *p)
{
    for (int i = 0; i <= p->last; i++)
        printf("%d ", p->data[i]);
    putchar(10);
}/*====================7、清空顺序表===================*/
void ClearSeqList(seqlist_t *p)    // for (int i = 0; i <= p->last; i++)
    // {
    //     if (p->data[i] == data) 
    //         return i;
    // }
    //  return -1; 
{
    p->last = -1;
}/*====================8、修改指定位置的数据====================*/
int ChangePostSeqList(seqlist_t *p,int post,int data)//post被修改的位置，data修改成的数据
{
    // 0.容错判断
    if (IsEpSeqlist(p) || post < 0 || post > p->last)
    {
        perror("ChangePostSeqList error");
        return -1;
    }
    // 1.将data复制给post位置
    p->data[post] = data;
    return 0;
}/*====================9、查找指定数据出现的位置===================*/
int SearchDataSeqList(seqlist_t *p,int data)//data代表被查找的数据
{
    /*-----有重复元素-----*/
    // int flag = 0;
    // for (int i = 0; i <= p->last; i++)
    // {
    //     if (p->data[i] == data)
    //     { 
    //         printf("%d出现在下标为%d的位置\n", data, i);
    //         flag = 1;
    //     }  
    // }
    // if (flag == 0)
    // {
    //     printf("数组中不存在%d\n", data);
    //     return 0; 
    // }
    // return 0;    /*-----没有重复元素-----*/
    // for (int i = 0; i <= p->last; i++)
    // {
    //     if (p->data[i] == data) 
    //         return i;
    // }
    //  return -1; 
}

main.c代码：

#include<stdio.h>
#include "seqlist.h"
int main(int argc, char const *argv[])
{
    seqlist_t *p = CreateEpSeqlist();
    int num = 0;
    for (int i = 0; i < N; i++)
    {
        printf("请输入第%d个元素:", i + 1);
        scanf("%d", &num);
        InsertIntoSeqlist(p, i, num);
    }
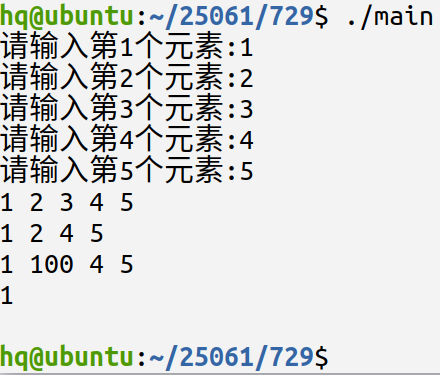
    ShowSeqlist(p);
    DeletePostSeqlist(p, 2);
    ShowSeqlist(p);
    ChangePostSeqList(p, 1, 100);
    ShowSeqlist(p);
    int loc = 0;
    loc = SearchDataSeqList(p, 100);
    printf("%d\n", loc);
    ClearSeqList(p);
    ShowSeqlist(p);
    free(p);
    p = NULL;
    return 0;
}

makefile文件：

EXE=main
FILES=$(wildcard *.c)
OBJS=$(patsubst %.c,%.o, $(FILES))
CC=gcc
CFLAGS=-c -g -Wall
$(EXE):$(OBJS)
	$(CC) $^ -o $@
%.o:%.c
	$(CC) $(CFLAGS) $< -o $@
.PHONY:clean
clean:
	$(RM) $(OBJS) $(EXE)

5、总结

1）内存：顺序表在内存中是连续存储的

2）长度：顺序表长度固定，#define N 5

3）复杂度：顺序表的插入和删除麻烦，查找和修改比较简单

三、栈

1、定义

只能在一端进行插入和删除操作的线性表（又称为堆栈），进行插入和删除操作的一端称为栈顶，另一端称为栈底

2、特点

先进后出 FILO first in last out

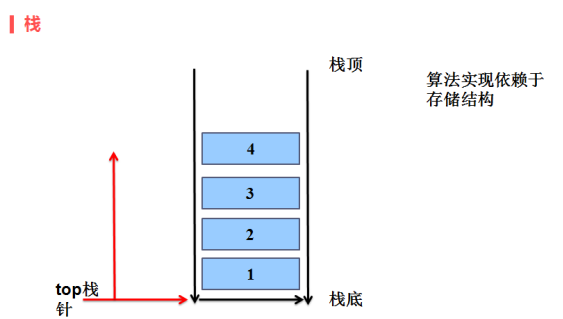
3、顺序栈

（1）逻辑结构：线性结构

（2）存储结构：顺序存储

（3）操作：入栈、出栈

​​​​​​​​​​​​​​结构体

​​​​​​​typedef struct seqstack

{

        int *data;         // data

        int maxlen;         // N

        int top;         // last

} seqstack_t;

头文件：

#ifndef _SEQSTACK_H_
#define _SEQSTACK_H_
#include<stdio.h>
#include<stdlib.h>
typedef struct seqstack
{
    int *data;  // 指向栈的存储位置
    int maxlen; // 保存栈的最大长度
    int top;    // 称为栈针，用的时候，可以将按照顺序表里的last来使用
                // top 始终代表当前栈内最后一个有效元素的下标
} seqstack_t;
// 1.创建一个空的栈
seqstack_t *CreateEpSeqStack(int len); // len代表的是创建栈的时候的最大长度
// 2.判断是否为满,满返回1 未满返回0
int IsFullSeqStack(seqstack_t *p);
// 3.入栈
int PushStack(seqstack_t *p, int data); // data代表入栈的数据
// 4.判断栈是否为空
int IsEpSeqStack(seqstack_t *p);
// 5.出栈
int PopSeqStack(seqstack_t *p);
// 6. 清空栈
void ClearSeqStack(seqstack_t *p);
// 7. 获取栈顶数据(注意不是出栈操作，如果出栈，相当于删除了栈顶数据，只是将栈顶的数据获取到，不需要移动栈针)
int GetTopSeqStack(seqstack_t *p);
// 8. 求栈的长度
int LengthSeqStack(seqstack_t *p);
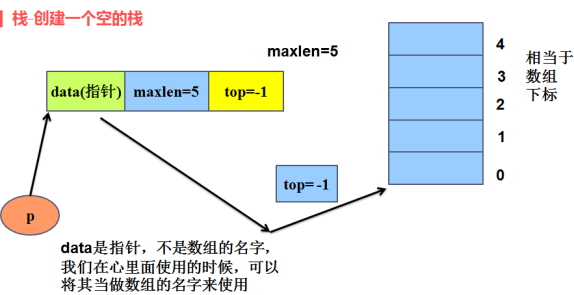
#endif

3.1 创建空的顺序栈

/*==================1、创建一个空的栈==================*/
seqstack_t *CreateEpSeqStack(int len)       // len代表的是创建栈的时候的最大长度
{
    // 1.开辟一个结构体大小的空间
    seqstack_t *p = (seqstack_t *)malloc(sizeof(seqstack_t));
    if (p == NULL)
    {
        perror("seqstack_t malloc err");   // 可以返回错误缘由
        return NULL;
    }
    // 2.初始化结构体成员
    p->maxlen = len;    // 最大长度，相当于宏定义的N
    p->top = -1;    // 指向最后一个有效元素的下标，相当于last
    p->data = (int *)malloc(len * sizeof(int)); // 开辟存放数组元素的空间，将首地址赋给结构体中指向数组首地址的指针
    if (p->data == NULL)
    {
        perror("data malloc err");   // 可以返回错误缘由
        free(p);    // 如果没开辟成功，结构体空间也没用，可以释放
        p = NULL;
        return NULL;
    }
    // 3.返回结构体空间的首地址
    return p;
}

3.2 入栈

第一步：容错判断，判满

第二步：移动栈针到有效数据位

第三步：通过将栈针位置赋值实现入栈

/*========2、判断是否为满,满返回1 未满返回0========*/
int IsFullSeqStack(seqstack_t *p)
{
    return p->top + 1 == p->maxlen;
}/*=======================3、入栈=======================*/
int PushStack(seqstack_t *p, int data)  // data代表入栈的数据
{
    // 1.容错判断
    if (IsFullSeqStack(p))
    {
        perror("PushStack error");
        return -1;
    }
    // 2.移动栈针
    p->top++;
    // 3.data入栈
    p->data[p->top] = data;
    return 0;
}

3.3 出栈

第一步：容错判断，判空

第二步：移动栈针到栈顶的下一个位置

第三步：通过返回栈针 + 1 位置数据，得到原来栈顶的数据

/*========4、判断栈是否为空========*/
int IsEpSeqStack(seqstack_t *p)
{
    return p->top == -1;
}/*=======================5、出栈=======================*/
int PopSeqStack(seqstack_t *p)
{
    // 1.容错判断
    if (IsEpSeqStack(p))
    {
        perror("PopSeqStack error");
        return -1;        
    }
    // 2.移动栈针
    p->top--;
    // 3.返回栈顶数据
    return p->data[p->top + 1];
}

3.4 其他操作

/*=================6、清空栈=================*/
void ClearSeqStack(seqstack_t *p)
{
   p->top = -1;
}
/*=================7、获取栈顶数据=================*/
// 注意不是出栈操作，如果出栈，相当于删除了栈顶数据，只是将栈顶的数据获取到，不需要移动栈针
int GetTopSeqStack(seqstack_t *p)
{
    // 1.容错判断（判空）
    if (IsEpSeqStack(p))
    {
        perror("GetTopSeqStack error");
        return -1;
    }
    // 2.获取栈顶数据
    return p->data[p->top];
}
/*=================8、求栈的长度=================*/
int LengthSeqStack(seqstack_t *p)
{
    return p->top + 1;   
}

3.5 主函数

#include"seqstack.h"
int main(int argc, char const *argv[])
{
    int i;
    seqstack_t *p = CreateEpSeqStack(5);
    for ( i = 1; i < 6; i++)
        PushStack(p, i);
    printf("top value:%d\n", GetTopSeqStack(p));
    printf("len is %d\n", LengthSeqStack(p));
    while (!IsEpSeqStack(p))
        printf("%d ", PopSeqStack(p));
    putchar(10);
    free(p->data);
    p->data = NULL;
    free(p);
    p = NULL;
    return 0;
}

3.6 练习

1. 若进栈顺序为 1,2,3,4 一下四种情况不可能出现的出栈序列是( C )

A. 1,4,3,2

B. 2,3,4,1

C. 3,1,4,2

D. 3,4,2,1

2. 下列叙述正确的是( A )

A. 线性表是线性结构

B. 栈与队列是非线性结构

C. 线性链表是非线性结构

D. 二叉树是线性结构

3. 下列关于栈叙述正确的是( D )

A.在栈中只能插入数据

B.在栈中只能删除数据

C.栈是先进先出的线性表

D.栈是先进后出的线性表

4、链式栈（无头链表）

1）逻辑结构：线性结构

2）存储结构：链式存储

3）操作：入栈、出栈

结构体：

typedef int datatype;

typedef struct linkstack

{

        datatype data;         ​​​​​​​        //数据域

        struct linkstack *next;         //指针域

} linkstack_t;

头文件：

#ifndef _LINKSTACK_H_
#define _LINKSTACK_H_//入栈和出栈只在第一个节点位置操作
typedef int datatype;
typedef struct linkstack
{
	datatype data;//数据域
	struct linkstack *next;//指针域
}linkstack_t;
//1.创建一个空的栈
void CreateEpLinkStack(linkstack_t **ptop);
//2.入栈   data是入栈的数据
参数上之所以采用二级指针，因为我们要随着入栈添加新的节点作为头，top需要永远指向当前链表的头，
那么修改main函数中的top，我们采用地址传递
int PushLinkStack(linkstack_t **ptop, datatype data);
//3.判断栈是否为空
int IsEpLinkStack(linkstack_t *top);
//4.出栈
datatype PopLinkStack(linkstack_t **ptop);
//5.清空栈
void ClearLinkStack(linkstack_t **ptop);//用二级指针，是因为清空后需要将main函数中的top变为NULL
//6.求栈的长度
int LengthLinkStack(linkstack_t *top);//用一级指针，是因为我只是求长度，不需要修改main函数中top指针的指向
//7.获取栈顶数据,不是出栈,不需要移动main函数中的top，所以用一级指针
datatype GetTopLinkStack(linkstack_t *top);
#endif

4.1 创建一个空栈

/*=============1、创建一个空的栈=============*/
void CreateEpLinkStack(linkstack_t **ptop)  // ptop == &top
{
    *ptop = NULL;   // top = NULL
}

4.2 入栈

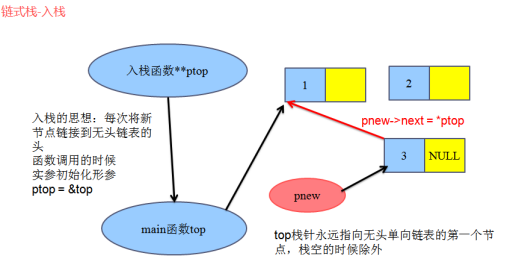
/*=============2、入栈  data是入栈的数据=============*/
// 参数上之所以采用二级指针，因为我们要随着入栈添加新的节点作为头，top需要永远指向当前链表的头，
// 那么修改main函数中的top，我们采用地址传递
int PushLinkStack(linkstack_t **ptop, datatype data)
{
    // 1.创建一个节点，并初始化
    linkstack_t *pnew = (linkstack_t *)malloc(sizeof(linkstack_t));
    if (pnew == NULL)
    {
        perror("PushLinkStack error");
        return -1;
    }
    pnew->data = data;
    pnew->next = NULL;
    // 2.入栈
    pnew->next = *ptop;
    // 3.移动栈针
    *ptop = pnew;
    return 0;
}

4.3 出栈 + 判空

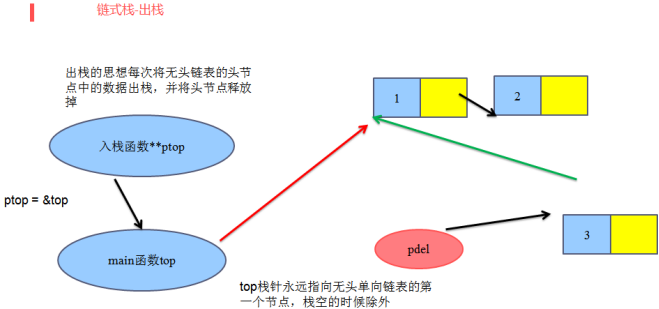
/*=============3、判断栈是否为空=============*/
int IsEpLinkStack(linkstack_t *top)
{
    return top == NULL;
}
/*=============4、出栈=============*/
datatype PopLinkStack(linkstack_t **ptop)
{
    // 1.容错判断（判空）
    if (IsEpLinkStack(*ptop))
    {
        perror("PopLinkStack error");
        return -1;
    }
    // 2.定义一个结构体类型的指针指向栈顶
    linkstack_t *pdel = *ptop;
    // 3.保存一下栈顶数据域的值
    datatype temp = 0;
    temp = pdel->data;
    // 4.移动栈针
    *ptop = pdel->next;
    // 5.释放删除的节点
    free(pdel);
    pdel = NULL;
    // 6.返回出栈数据
    return temp;
}

4.4 清空栈

/*=============5、清空栈=============*/
void ClearLinkStack(linkstack_t **ptop)//用二级指针，是因为清空后需要将main函数中的top变为NULL
{
    while (*ptop != NULL)
        PopLinkStack(ptop);
}

4.5 求栈长

/*=============6、求栈的长度=============*/
int LengthLinkStack(linkstack_t *top)//用一级指针，是因为我只是求长度，不需要修改main函数中top指针的指向
{
    int len = 0;
    while (top != NULL)
    {
        len++;
        top = top->next;
    }
    return len;
}

4.6 获取栈顶数据

/*===7、获取栈顶数据,不是出栈,不需要移动main函数中的top，所以用一级指针===*/
datatype GetTopLinkStack(linkstack_t *top)
{
    if(top != NULL)
        return top->data;
    return -1;
}

4.7 主函数

int main(int argc, char const *argv[])
{
    linkstack_t *top;
    CreateEpLinkStack(&top);
    for (int i = 1; i < 6; i++)
        PushLinkStack(&top, i);
    printf("top is %d\n", GetTopLinkStack(top));
    printf("len is %d\n", LengthLinkStack(top));
    for (int i = 1; i < 6; i++)
        printf("%d ", PopLinkStack(&top));
    putchar(10);
    ClearLinkStack(&top);
    printf("len is %d\n", LengthLinkStack(top));
    return 0;
}

5、总结

顺序栈和链式栈的区别：

1）存储结构不同，顺序栈相当于数组，内存连续，链式栈用链表存储，内存不连续

2）顺序栈长度受限制，而链式栈不会受限制

四、链表

特点：内存不连续，通过指针连接

解决：长度固定的问题、插入和删除麻烦的问题

1）逻辑结构：线性结构

2）存储结构：链式存储

3）操作：增删改查

1、单向链表

结构体：

struct node_t

{

        int data;                         //数据域

        struct node_t * next;         //指针域，指向下一个节点

}；

1.1 分类

1.1.1 有头单向链表

存在一个头节点，数据域无效 指针域有效

#include <stdio.h>
typedef struct node_t
{
    int data;
    struct node_t *next;
} link_node_t, *link_list_t;    // 重新定义结构体名字，重新定义结构体类型的指针的名字
int main(int argc, char const *argv[])
{
    // 1.定义3个节点
    link_node_t a = {1, NULL};
    link_node_t b = {2, NULL};
    link_node_t c = {3, NULL};
    // 2.将节点进行连接
    a.next = &b;
    b.next = &c;
    // 3.定义一个头节点，头节点指向a节点
    link_node_t s;
    s.next = &a;
    // 4.定义一个头指针，指向头节点
    link_list_t h = &s;
    // 5.遍历有头单向链表
    while (h->next != NULL)
    {
        h = h->next;
        printf("%d ", h->data);
    }
    putchar(10);
    return 0;
}

重点：遍历有头单向链表！！！！！！！

while (h->next != NULL)

{

h = h->next;

printf("%d ", h->data);

}

putchar(10);

1.1.2 无头单向链表

所有节点的数据域、指针域均有效

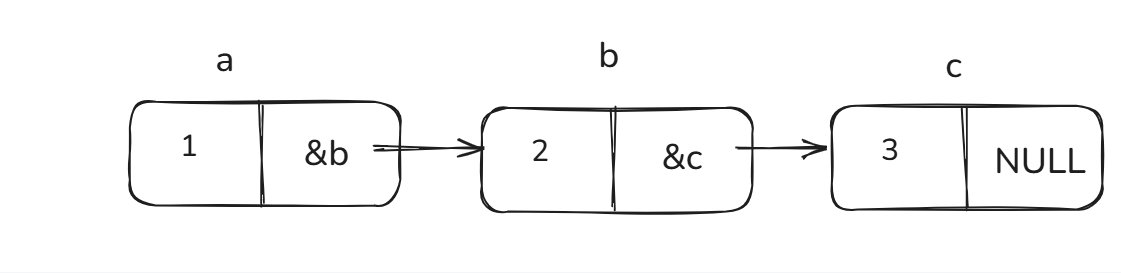
#include <stdio.h>
typedef struct node_t
{
    int data;
    struct node_t *next;
} link_node_t, *link_list_t;    // 重新定义结构体名字，重新定义结构体类型的指针的名字
int main(int argc, char const *argv[])
{
    // 1.定义3个节点
    link_node_t a = {1, NULL};
    link_node_t b = {2, NULL};
    link_node_t c = {3, NULL};
    // 2.将节点进行连接
    a.next = &b;
    b.next = &c;
    // 3.定义一个头指针，指向第一个节点
    link_list_t h = &a;
    // 4.遍历无头单向链表
    while (h != NULL)
    {
        printf("%d ", h->data); 
        h = h->next;
    }
    putchar(10);
    return 0;
}

1.2 操作函数（以有头单向链表为例）

结构体：

typedef int datatype;        // 对数据类型重定义

typedef struct node_t

{

        datatype data;                        //数据域

        struct node_t *next;                //指针域,指向自身结构体的指针

}link_node_t,*link_list_t;

头文件：

#ifndef _LINKLIST_H_
#define _LINKLIST_H_#include<stdio.h>
#include<stdlib.h>typedef int datatype;
typedef struct node_t
{
	datatype data;//数据域
	struct node_t *next;//指针域,指向自身结构体的指针
}link_node_t,*link_list_t;//1.创建一个空的单向链表(有头单向链表)
link_node_t *CreateEpLinkList();
//2.向单向链表的指定位置插入数据
//p保存链表的头指针 post 插入的位置 data插入的数据
int InsertIntoPostLinkList(link_node_t *p,int post, datatype data);
//3.遍历单向链表
void ShowLinkList(link_node_t *p);
//4.求单向链表长度的函数
int LengthLinkList(link_node_t *p);
//5.删除单向链表中指定位置的数据 post 代表的是删除的位置
int DeletePostLinkList(link_node_t *p, int post);
//6.判断单向链表是否为空 1代表空 0代表非空
int IsEpLinkList(link_node_t *p);
//7.修改指定位置的数据 post 被修改的位置 data修改成的数据
int ChangePostLinkList(link_node_t *p, int post, datatype data);
//8.查找指定数据出现的位置 data被查找的数据 //search 查找
int SearchDataLinkList(link_node_t *p, datatype data);
//9.删除单向链表中出现的指定数据,data代表将单向链表中出现的所有data数据删除
int DeleteDataLinkList(link_node_t *p, datatype data);
//10.转置链表
void ReverseLinkList(link_node_t *p);
//11.清空单向链表
void ClearLinkList(link_node_t *p);
#endif
1）创建一个空的有头单向链表

/*=========1、创建一个空的单向链表(有头单向链表)=========*/
link_node_t *CreateEpLinkList()
{
    // 1.开辟结构体大小的空间
    link_list_t p = (link_list_t)malloc(sizeof(link_node_t));
    if (p == NULL)
    {
        perror("malloc err"); // 可以返回错误缘由
        return NULL;
    }
    // 2.初始化
    p->next = NULL;
    // 3.返回头结点
    return p;
}
2）求单向链表的长度、向post位置插入一个数据

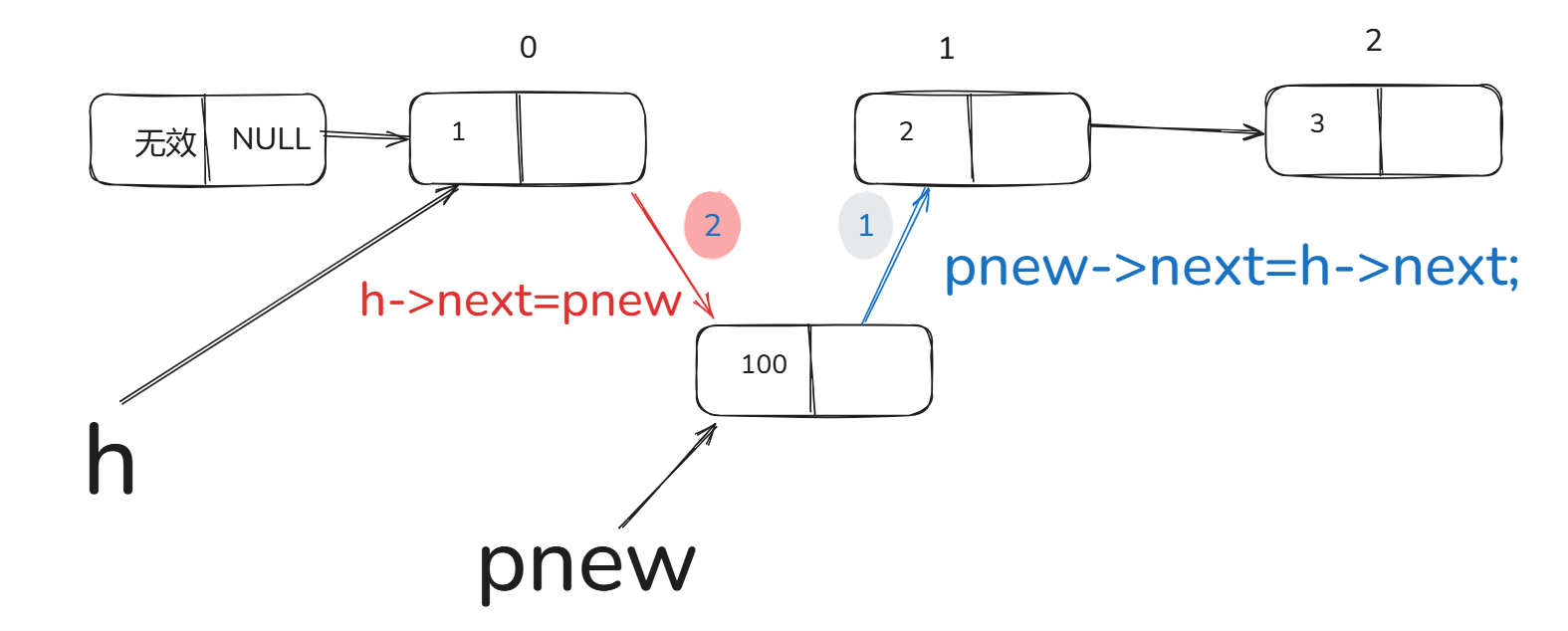
        先遍历找到要插入节点的前一个节点，假设这个节点为A，A的下一个节点为B，将C插入A与B之间，想要完成此操作需要先让C的指针域指向B，再让A的指针域指向C

/*=========4、求单向链表长度的函数===========*/
int LengthLinkList(link_node_t *p)
{
    int len = 0;
    while (p->next != NULL)
    {
        p = p->next;
        len++;
    }
    return len;
}/*=========2、向单向链表的指定位置插入数据=========*/
//p保存链表的头指针 post 插入的位置 data插入的数据
int InsertIntoPostLinkList(link_node_t *p,int post, datatype data)
{
    int i;   
    // 1.容错判断(post < 0 或者 post > len)
    if (post < 0 || post > LengthLinkList(p))
    {
        perror("InsertIntoPostLinkList error");
        return -1;
    }
    // 2.将头指针指向被插入位置的前一个节点
    for ( i = 0; i < post; i++)
        p = p->next;
    // 3.创建一个新节点，并初始化
    link_list_t pnew = (link_list_t)malloc(sizeof(link_node_t));
    if (pnew == NULL)
    {
        perror("pnew malloc err"); // 可以返回错误缘由
        return -1;
    }
    pnew->data = data;
    pnew->next = NULL;
    // 4.将新节点插入到链表中（先连后再连前）
    pnew->next = p->next;
    p->next = pnew;
    return 0;
}
3）删除指定位置数据

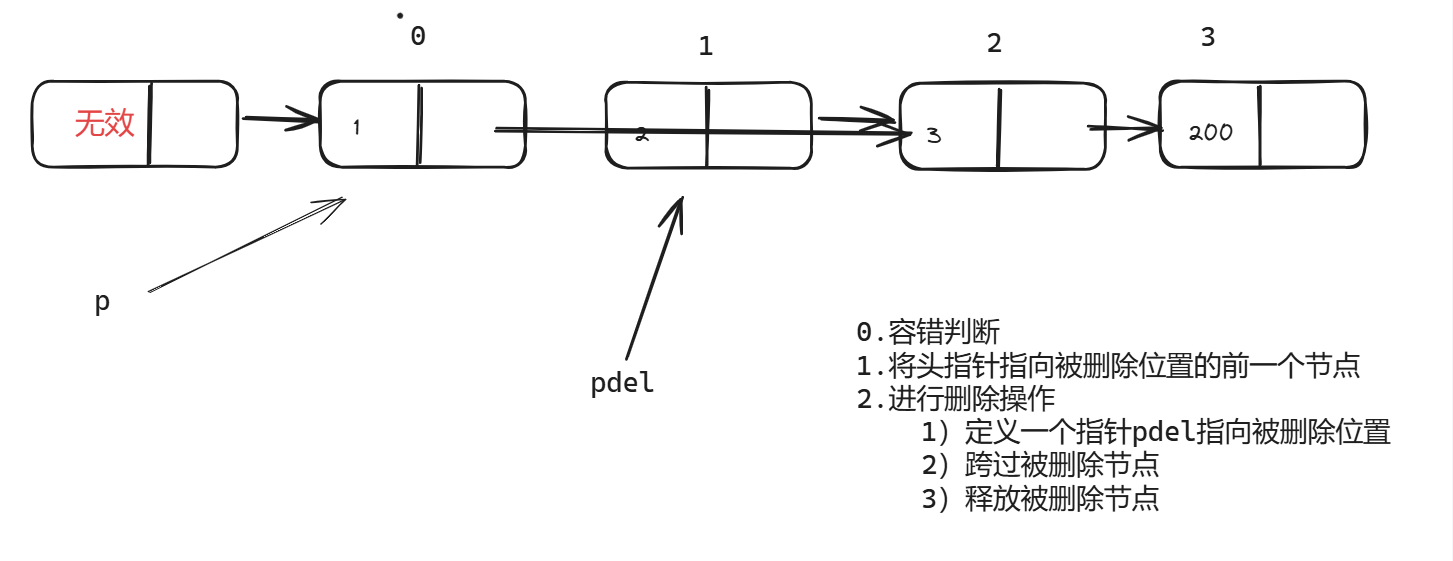
/*=======6、判断单向链表是否为空 1代表空 0代表非空=======*/
int IsEpLinkList(link_node_t *p)
{
    return !LengthLinkList(p);
}
/*===5、删除单向链表中指定位置的数据 post 代表的是删除的位置===*/
int DeletePostLinkList(link_node_t *p, int post)
{
    int i;
    // 1.容错判断(判空、post)
    if (IsEpLinkList(p) || post >= LengthLinkList(p))
    {
        perror("DeletePostLinkList error");
        return -1;
    }
    // 2.将头指针指向被删除位置的前一个节点
    for ( i = 0; i < post; i++)
        p = p->next;
    // 3.进行删除操作
    // 1）定义一个指针pdel指向被删除节点
    link_list_t pdel = p->next;
    // 2)跨过被删除的节点
    p->next = pdel->next;
    // 3）释放被删除的节点
    free(pdel);
    pdel = NULL;
    return 0;
}
4）清空列表
/*=============11、清空单向链表=============*/
void ClearLinkList(link_node_t *p)
{
    while (!IsEpLinkList(p))
        DeletePostLinkList(p, 0);
}
5）单向列表的转置（重点）

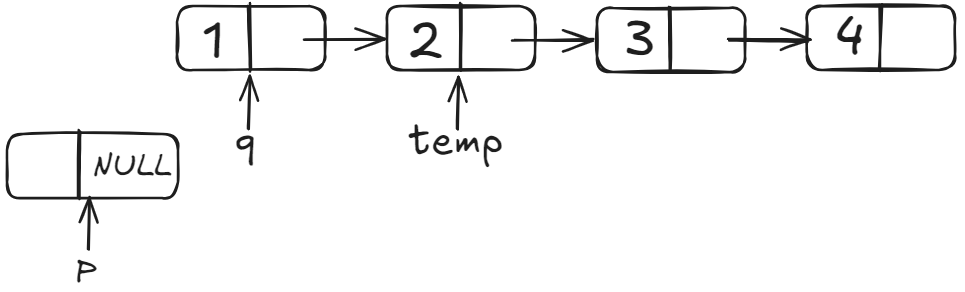
解题思想：

①将头节点与当前链表断开，断开前保存下头节点的下一个节点，保证后面链表能找得到，定义一个q保存头节点的下一个节点，断开后前面相当于一个空的链表，后面是一个无头的单向链表

②遍历无头链表的所有节点，将每一个节点当做新节点插入空链表头节点的下一个节点(每次插入的头节点的下一个节点位置)

/*=============10、转置链表=============*/
void ReverseLinkList(link_node_t *p)
{
    // 1.断头前，先定义一个指针q指向头节点的下一个节点
    link_list_t q = p->next;
    link_list_t temp = NULL;
    // 2.执行断头，相当于有头空链表，无头链表
    p->next = NULL; /*地址域为NULL相当于断头*/
    // 3.遍历无头链表，依次头插到头节点后面
    while (q != NULL)   /*q = temp，所以q不为空即可进入*/
    {
        temp = q->next; /*先让中间指针指向无头链表的下一个节点*/
        q->next = p->next;  /*先连后面*/
        p->next = q;    /*再连前面*/
        q = temp;   /*再让q重新指回无头链表的节点*/
    }
}
6）修改指定位置数据
/*===7、修改指定位置的数据 post 被修改的位置 data修改成的数据===*/
int ChangePostLinkList(link_node_t *p, int post, datatype data)
{
    int i;
    // 1.容错判断（判空、post）
    if (IsEpLinkList(p) || post >= LengthLinkList(p))
    {
        perror("DeletePostLinkList error");
        return -1;
    }
    // 2.将头指针指向被修改位置的节点
    for ( i = 0; i <= post; i++)
        p = p->next;    
    // 3.修改数据
    p->data = data;
    return 0;
}
7）查找指定数据出现的位置
/*===8、查找指定数据出现的位置 data被查找的数据===*/
int SearchDataLinkList(link_node_t *p, datatype data)
{
    int post = 0;
    while (p->next != NULL)
    {
        p = p->next;
        if (data == p->data)
            return post;
        post++;
    }
    return -1;
}
8）删除指定元素
/*===9、删除单向链表中出现的指定数据,data代表将单向链表中出现的所有data数据删除===*/
int DeleteDataLinkList(link_node_t *p, datatype data)
{
    // 1.定义一个指针q指向头节点的下一个节点，此时可以看做q指向一个无头单向链表
    link_list_t q = p->next;
    // 2.用q遍历链表，将每一个节点的数据域和data比较，如果相同就删掉该节点
    while (q != NULL)   /*q只要不是空就可以进入循环*/
    {
        if (q->data == data)    /*判断q指向的数据域是否和data相等*/
        {
            p->next = q->next;  /*如果相等，则直接跳过需要删除的节点*/
            free(q);            /*删除节点之后可以对删除的节点空间进行释放*/
            q = p->next;        /*释放结束后，可以不用置空，直接赋值为p的下一个节点*/
        }
        else    /*如果q指向的数据和data不相等则进入*/
        {
            p = p->next;    
            q = p->next;
        }
    }
    return 0;
}
9）遍历单向链表
/*============3、遍历单向链表============*/
void ShowLinkList(link_node_t *p)
{
    while (p->next != NULL)
    {
        p = p->next;
        printf("%d ", p->data);
    }
    putchar(10);
}
10）主函数
#include"linklist.h"
int main(int argc, char const *argv[])
{
    link_list_t h = CreateEpLinkList();
    for(int i = 0; i < 5; i++)
        InsertIntoPostLinkList(h, i, i + 1);
    printf("len is %d\n", LengthLinkList(h));
    ShowLinkList(h);
    ReverseLinkList(h);
    ShowLinkList(h);
    DeletePostLinkList(h, 2);
    ShowLinkList(h);
    ChangePostLinkList(h, 2, 3);
    ShowLinkList(h);
    printf("位置：%d\n", SearchDataLinkList(h, 5));
    return 0;
}

1.3 顺序表和链表的区别

(1)顺序表在内存当中连续存储的(数组)，但是链表在内存当中是不连续存储的，通过指针将数据链接在一起

(2)顺序表的长度是固定的，但是链表长度不固定

(3)顺序表查找方便，但是插入和删除麻烦，链表，插入和删除方便，查找麻烦

1.4 练习

1、向一个单链表linklist中的节点t后面插入一个节点p，下列操作正确的是( B )

a)t->next = p->next;t->next = p;

b)p->next = t->next;t->next = p;

c)t->next = p;p->next = t->next;

d)t->next = p;t->next = p->next;

2、已知单向链表中a,b两个节点，无法得到头节点，如何删除a节点？

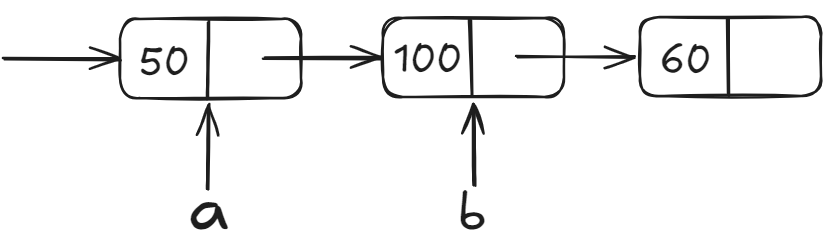
解析：可以将释放节点和删除数据分为两步看

第一步 ===> 将b指向的数据域赋值给a指向的数据域，实现将a存储的数据删除

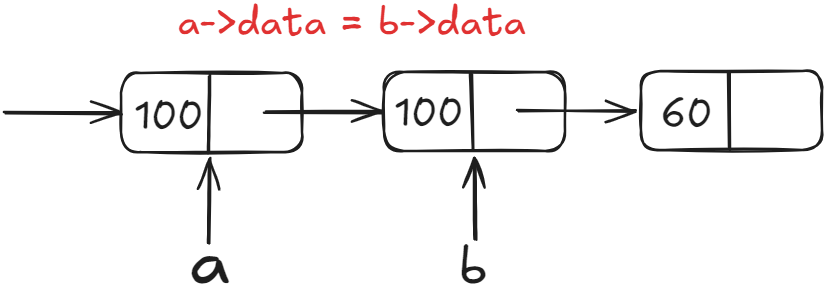
第二步 ===> 将b节点跨过，让a直接指向b的下一节点，为释放b做准备

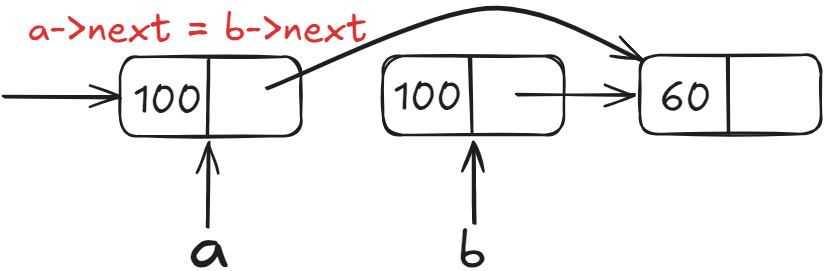
第三步 ===> 释放b节点，从而实现a节点的删除

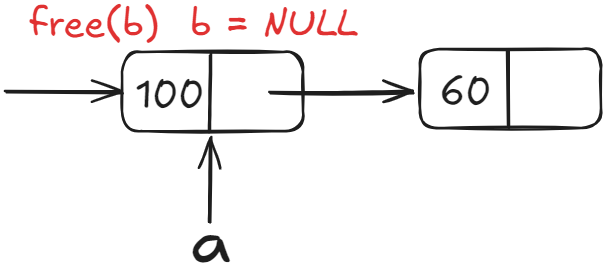
2、单向循环链表

解决约瑟夫问题

约瑟夫问题为：设编号为1，2，……n得n个人围坐一圈，约定编号为k（k大于等于1并且小于等于n）的人从1开始报数，数到m的那个人出列。它的下一位继续从1开始报数，数到m的人出列，依次类推，最后剩下一个为猴王。

直接图展示，初始化状态： 假设n=6，总共有6个人，k=1,从第一个人开始报数，m=5,每次数五个。

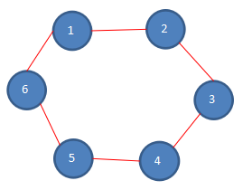
  第一次报数：从一号开始，数五个数，1-2-3-4-5，数完五个数，五号被杀死，第一次报数后，剩余人数如下。

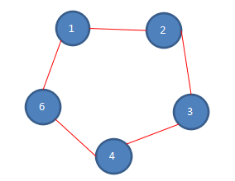
第二次报数： 从被杀死的五号的下一位开始报数，也就是六号，数五个数，6-1-2-3-4，数数完毕，四号被杀死，第二次报数后，剩余人数如下

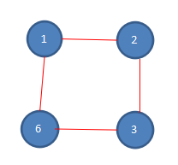
第三次报数： 从被杀死的四号的下一位开始报数，同样是六号，数五个数，6-1-2-3-6，数数完毕，六号被杀死，第三次报数后，剩余人数如下。

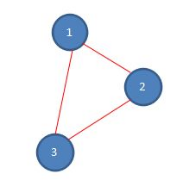
第四次报数： 从被杀死的六号的下一位开始报数，也就是一号，数五个数，1-2-3-1-2，数数完毕，二号被杀死，第四次报数后，剩余人数如下。

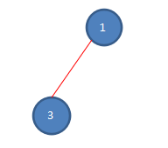
第五次报数： 从被杀死的二号的下一位开始报数，也就是三号，数五个数，3-1-3-1-3，数数完毕，三号被杀死，只剩下一号

#include <stdio.h>
#include <stdlib.h>
typedef struct node_t
{int data;struct node_t *next;
}link_node_t,*link_list_t;
int main(int argc, const char *argv[])
{int i;
	link_list_t pdel = NULL;//用于指向被删除节点
	link_list_t ptail = NULL;//永远指向当前链表的尾 
	link_list_t pnew = NULL;//永远指向新创建的节点
	link_list_t h = NULL;int all_num = 7;//猴子总数 int start_num = 2; //从几号猴子开始数int kill_num = 3;//数到几杀死猴// printf("请您入猴子总数 起始号码 数到几杀死:\n");// scanf("%d%d%d",&all_num,&start_num,&kill_num);//1.创建出一个单向循环链表//(1)创建有all_num个节点的单向链表
	h = (link_list_t)malloc(sizeof(link_node_t));if(NULL == h){perror("malloc failed");return -1;}
	h->data = 1;
	h->next = NULL;
	ptail = h;//尾指针指向当前的第一个节点for(i = 2; i <= all_num; i++){//创建新的节点
		pnew = (link_list_t)malloc(sizeof(link_node_t));if(NULL == pnew){perror("malloc failed");return -1;}//将新节点装上数据
		pnew->data = i;
		pnew->next = NULL;//将新节点链接到链表尾 
		ptail->next = pnew;//链接到链表的尾
		ptail = pnew;//尾指针继续指向当前链表的尾 }//(2)将头指针保存到链表的尾形成单向循环链表
	ptail->next = h;//形成单向循环链表 
#if 0 //用于调试程序while(1){printf("%d\n",h->data);
		h = h->next;sleep(1);}
#endif//2.开始杀猴子 //(1)将头指针移动到开始猴子的号码处 for(i = 0; i < start_num-1; i++)
		h = h->next;//(2)循环进行杀猴子while(h != h->next)//条件不成的时候，就剩一个猴子,只有一个节点{//将头指针移动到即将删除节点的前一个节点for(i = 0; i < kill_num-2; i++)
			h = h->next;		pdel = h->next;//跨过删除节点
		h->next = pdel->next;printf("kill is -------------%d\n",pdel->data);free(pdel);
		pdel = NULL;//杀死猴子猴，从下一个节点开始继续开始数,将头指针移动到开始数的地方
		h = h->next;}printf("king is=================== %d\n",h->data);return 0;
}

3、双向链表（有头）

结构体：

​​​​​​​​​​​​​​typedef int datatype;

typedef struct node_t

{

        datatype data;         ​​​​​​​        // 数据域

        struct node_t *next;         // 指向下一个节点的指针 next 下一个

        struct node_t *prior;         // 指向前一个节点的指针 prior 先前的

} link_node_t, *link_list_t;

//将双向链表的头指针和尾指针封装到一个节点体里

//思想上有点像学的链式队列

typedef struct doublelinklist

{

        link_list_t head;                  //指向双向链表的头指针

        link_list_t tail;                          //指向双向链表的尾指针

        int len;                                 //用来保存当前双向链表的长度（可省略）

} double_node_t, *double_list_t;

头文件：

#include <stdio.h>
#include <stdlib.h>
typedef int datatype;	
typedef struct node_t
{
datatype data;//数据域 
struct node_t *next;//指向下一个节点的指针 next 下一个
struct node_t *prior;//指向前一个节点的指针 prior 前一个
}link_node_t,*link_list_t;
//将双向链表的头指针和尾指针封装到一个结构体里 
//思想上有点像学的链式队列
typedef struct doublelinklist
{
link_list_t head; //指向双向链表的头指针
link_list_t tail; //指向双向链表的尾指针
int len;
}double_node_t,*double_list_t;
//1.创建一个空的双向链表
double_list_t createEmptyDoubleLinkList();
//2.向双向链表的指定位置插入数据 post位置， data数据
int insertIntoDoubleLinkList(double_list_t p, int post, datatype data);
//3.遍历双向链表
void showDoubleLinkList(double_list_t p);
//4.删除双向链表指定位置的数据
int deletePostDoubleLinkList(double_list_t p, int post);
//5.判断双向链表是否为空
int isEmptyDoubleLinkList(double_list_t p);
//6.求双向链表的长度
int lengthDoubleLinkList(double_list_t p);
//7.查找指定数据出现的位置 data被查找的数据
int searchPostDoubleLinkList(double_list_t p,datatype data);
//8.修改指定位置的数据,post修改的位置 data被修改的数据
int changeDataDoubleLinkList(double_list_t p,int post, datatype data);
//9.删除双向链表中的指定数据 data代表删除所有出现的data数据
int deleteDataDoubleLinkList(double_list_t p, datatype data);

3.1 创建空的双向链表

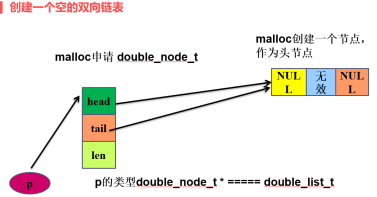
/*==============1.创建一个空的双向链表==============*/
double_list_t createEmptyDoubleLinkList()
{
    // 1.开辟一个存放头尾指针结构体的空间
    double_list_t p = (double_list_t)malloc(sizeof(double_node_t));
    if (p == NULL)
    {
        perror("double_list_t error");
        return NULL;
    }
    // 2.对头尾指针初始化
    p->head = (link_list_t)malloc(sizeof(link_node_t));
    p->tail = p->head;
    p->len = 0;     // 空链表，长度为0
    if (p->head == NULL)
    {
        perror("link_list_t error");
        free(p);
        p = NULL;
        return NULL;
    }
    // 3.头结点初始化
    p->head->next = NULL;
    p->head->prior = NULL;
    // 4.返回存放头尾指针结构体的首地址
    return p;
}

3.2 指定位置插入数据

3.2.1 尾插

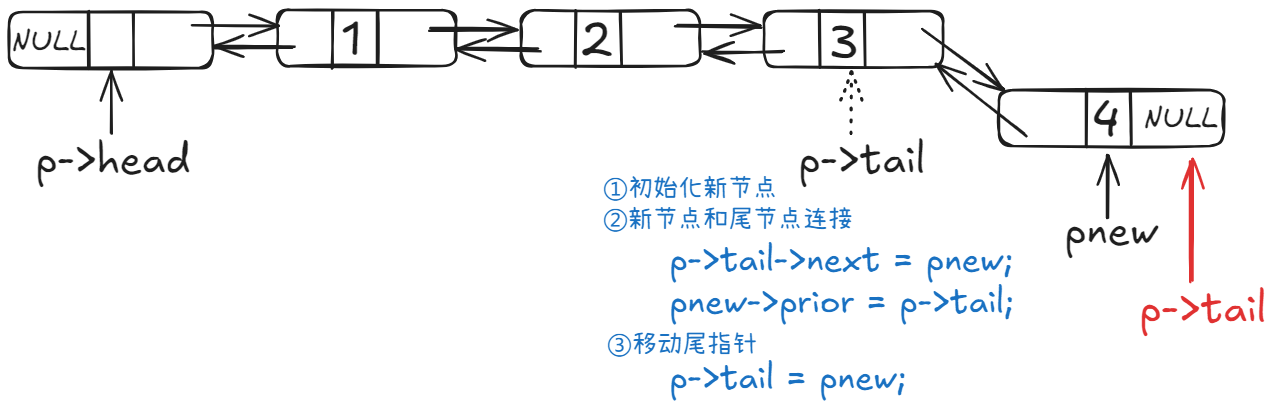
3.2.2 中间插

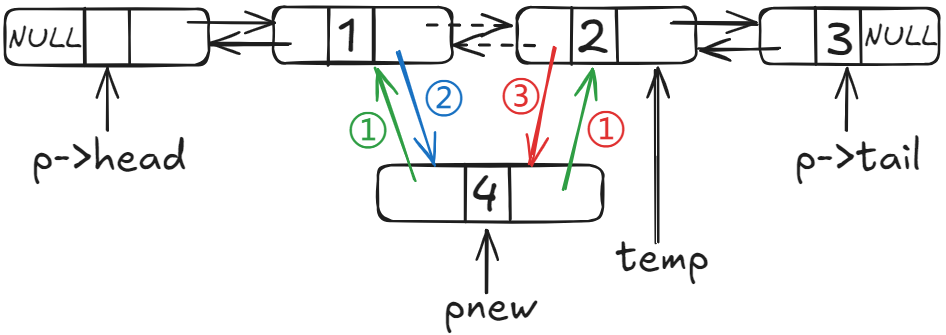
/*==============2.向双向链表的指定位置插入数据 post位置， data数据==============*/
int insertIntoDoubleLinkList(double_list_t p, int post, datatype data)
{
    int i;
    // 1.容错判断（post位置）
    if (post < 0 || post > p->len)
    {
        perror("insertIntoDoubleLinkList error");
        return -1;
    }
    // 2.创建新节点并初始化
    link_list_t pnew = (link_list_t)malloc(sizeof(link_node_t));
    if (pnew == NULL)
    {
        perror("link_list_t error");
        return -1;
    }
    pnew->data = data;
    pnew->next = NULL;
    pnew->prior = NULL;
    // 3.插入数据
    // 1）尾插
    if (post == p->len)
    {
        p->tail->next = pnew;
        pnew->prior = p->tail;
        // 移动尾指针
        p->tail = pnew;
    }
    // 2）中间插
    else
    {
        link_list_t temp = NULL; // 定义一个新指针代替头尾指针移动
        // 1>移动指针到被插入位置
        if (post < p->len / 2) // 插入位置在前半段
        {
            temp = p->head;     // 新指针代替头指针
            for ( i = 0; i <= post; i++)
                temp = temp->next;
        }
        else                    // 插入位置在后半段
        {
            temp = p->tail;     // 新指针代替尾指针
            for ( i = 0; i < p->len - post - 1; i++)
                temp = temp->prior;            
        }
        // 2>进行插入操作，先将 pnew 头尾和对应节点相连，再将原节点对应连接 pnew
        pnew->next = temp;
        pnew->prior = temp->prior;
        temp->prior->next = pnew;
        temp->prior = pnew;       
    }
    p->len++;
    return 0;
}

3.3 删除指定位置数据

3.3.1 尾删

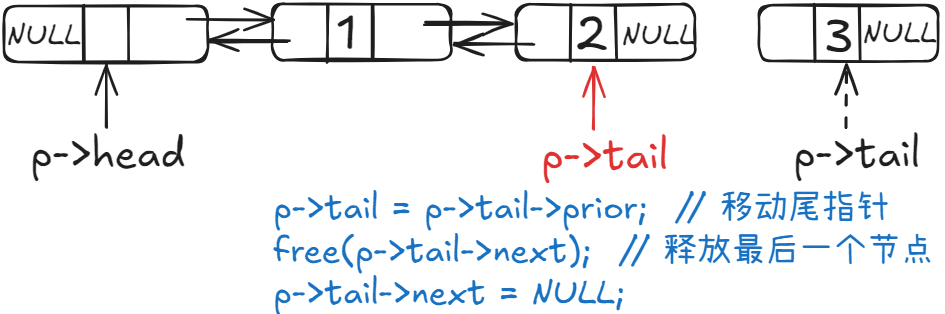
3.3.2 中间删

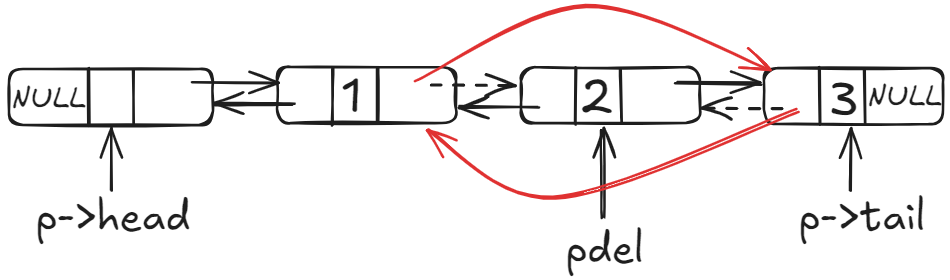
/*==============4.删除双向链表指定位置的数据==============*/
int deletePostDoubleLinkList(double_list_t p, int post)
{
int i;
    // 1.容错判断（post位置）
    if (post < 0 || post >= p->len)
    {
        perror("deletePostDoubleLinkList error");
        return -1;
    }
    // 2.删除数据
    // 1）尾删
    if (post == p->len - 1)
    {
        // 移动尾指针
        p->tail = p->tail->prior;
        // 删除尾节点
        free(p->tail->next);
        // 释放尾节点
        p->tail->next = NULL;
    }
    // 2）中间删
    else
    {
        link_list_t pdel = NULL; // 定义一个新指针代替头尾指针移动
        // 1>移动指针到被删除位置
        if (post < p->len / 2) // 删除位置在前半段
        {
            pdel = p->head;     // 新指针代替头指针
            for ( i = 0; i <= post; i++)
                pdel = pdel->next;
        }
        else                    // 删除位置在后半段
        {
            pdel = p->tail;     // 新指针代替尾指针
            for ( i = 0; i < p->len - post - 1; i++)
                pdel = pdel->prior;            
        }
        // 2>进行删除操作，跨过需要删除的节点
        pdel->prior->next = pdel->next;
        pdel->next->prior = pdel->prior;
        free(pdel);
        pdel = NULL;
    }
    p->len--;
    return 0;    
}

3.4 求双向链表长度

/*==============6.求双向链表的长度==============*/
int lengthDoubleLinkList(double_list_t p)
{
    return p->len;
}

3.5 查找指定数据出现位置

/*=======7.查找指定数据出现的位置 data被查找的数据=======*/
int searchPostDoubleLinkList(double_list_t p,datatype data)
{
    link_list_t temp = p->head;
    int post = 0;
    while (temp->next != NULL)
    {
        temp = temp->next;
        if (temp->data == data)
            return post;
        post++;
    }
    return -1;
}

3.6 修改指定位置数据

/*=====8.修改指定位置的数据,post修改的位置 data被修改的数据=====*/
int changeDataDoubleLinkList(double_list_t p,int post, datatype data)
{
    int i;
    // 1.容错判断（post位置）
    if (post < 0 || post >= p->len)
    {
        perror("changeDataDoubleLinkList error");
        return -1;
    }
    link_list_t temp = NULL; // 定义一个新指针代替头尾指针移动
    // 2.修改数据
    // 1>移动指针到被修改位置
    if (post < p->len / 2) // 修改位置在前半段
    {
        temp = p->head;     // 新指针代替头指针
        for ( i = 0; i <= post; i++)
            temp = temp->next;
    }
    else                    // 修改位置在后半段
    {
        temp = p->tail;     // 新指针代替尾指针
        for ( i = 0; i < p->len - post - 1; i++)
            temp = temp->prior;            
    }
    // 2>修改指定位置数据
    temp->data = data;
    return 0;
}

3.7 删除指定数据

/*==9.删除双向链表中的指定数据 data代表删除所有出现的data数据==*/
int deleteDataDoubleLinkList(double_list_t p, datatype data)
{
    link_list_t h = p->head->next;
    link_list_t pdel = NULL;
    while (h != NULL)
    {
        // 是否删除节点
        // 1）删除
        if (h->data == data)
        {
            // 1>尾删
            if (h == p->tail)
            {
                p->tail = p->tail->prior;
                free(p->tail->next);
                p->tail->next = NULL;
                h = NULL;
            }
            // 2>中间删
            else
            {
                h->prior->next = h->next;
                h->next->prior = h->prior;
                pdel = h;   // pdel指向被删除的节点
                h = h->next;    //h继续遍历
                free(pdel);     // 释放被删除节点   /*不能使用free(h->prior),因为此时已经找不到被删除的节点*/
                pdel = NULL;
            }
            p->len--;
        }
        // 2)不删
        else
            h = h->next;
    }    
    return 0;
}

3.8 遍历双向链表

/*==============3.遍历双向链表==============*/
void showDoubleLinkList(double_list_t p)
{
    // 正向遍历
    printf("正向遍历：");
    link_list_t temp = p->head;
    while (temp->next != NULL)
    {
        temp = temp->next;
        printf("%d ", temp->data);
    }
    putchar(10);
    // 反向遍历
    printf("反向遍历：");
    temp = p->tail;
    while (temp != p->head)
    {
        printf("%d ", temp->data);
        temp = temp->prior;
    }
    putchar(10);
}​​​​​​​

3.9 判空

/*==============5.判断双向链表是否为空==============*/
int isEmptyDoubleLinkList(double_list_t p)
{
    return p->len == 0;// return p->head == p->tail;
}

4、双向循环链表

双向循环链表	解决约瑟夫问题
#include <stdio.h>
#include <stdlib.h>typedef int datatype;
typedef struct node_t
{
	datatype data;
	struct node_t * prior;
	struct node_t * next;
}link_node_t,*link_list_t;typedef struct doublelinklist
{
	link_list_t head;
	link_list_t tail;
}double_node_t,*double_list_t;int main(int argc, const char *argv[])
{
	int i;
	int all_num = 8;//猴子总数
	int start_num = 3;//从3号猴子开始数
	int kill_num = 3;//数到几杀死猴子 
	link_list_t h = NULL;
	link_list_t pdel = NULL;//用来指向被杀死猴子的节点
	printf("请您输入猴子的总数，开始号码，出局号码:\n");
	scanf("%d%d%d",&all_num,&start_num,&kill_num);
	//1.创建一个双向的循环链表
	double_list_t p = (double_list_t)malloc(sizeof(double_node_t));//申请头指针和尾指针
	if(NULL == p)
	{
		perror("malloc failed");
		return -1;
	}
	p->head = p->tail = (link_list_t)malloc(sizeof(link_node_t));
	if(NULL == p->tail)
	{
		perror("p->tail malloc failed");
		return -1;
	}
	p->head->data = 1;
	p->head->prior = NULL;
	p->head->next = NULL;
	//将创建n个新的节点，链接到链表的尾
	for(i = 2; i <= all_num; i++)
	{
		link_list_t pnew = (link_list_t)malloc(sizeof(link_node_t));
		if(NULL == pnew)
		{
			perror("pnew malloc failed");
			return -1;
		}
		pnew->data = i;
		pnew->prior = NULL;
		pnew->next = NULL;
		//(1)将新的节点链接到链表的尾
		p->tail->next = pnew;
		pnew->prior = p->tail;
		//(2)尾指针向后移动，指向当前链表的尾
		p->tail = pnew;
	}
	//(3)形成双向循环链表 
	p->tail->next = p->head;
	p->head->prior = p->tail;
	//调试程序 
#if 0
	while(1)
	{
		printf("%d\n",p->head->data);
		p->head = p->head->next;
		sleep(1);
	}
#endif
	//2.循环进行杀死猴子
	h = p->head;
	//(1)先将h移动到start_num处，也就是开始数数的猴子号码处
	for(i = 0; i < start_num-1; i++)
		h = h->next;
	while(h->next != h)//当h->next == h 就剩一个节点了，循环结束
	{
		//(2)将h移动到即将杀死猴子号码的位置
		for(i = 0; i < kill_num-1; i++)
			h = h->next;
		//(3)进行杀死猴子，经过上面的循环后，此时的h指向即将杀死的猴子
		h->prior->next = h->next;
		h->next->prior = h->prior;
		pdel = h;//pdel指向被杀死猴子的位置
		printf("kill is -------%d\n",pdel->data);
		h = h->next;//需要移动，从杀死猴子后的下一个位置开始数
		free(pdel);
	}
	printf("猴王是%d\n",h->data);
	return 0;
}
  • 练习

1.一个函数想要给函数的调用者传递值有 返回值 和 地址传参 两种方式？

2.如何避免头文件重复包含？

#ifndef _***_H_

#define _***_H_

///

///

///

#endif

3.顺序表和链表的相同点和不同点有哪些？

相同点： 都是线性表 逻辑结构：线性结构 一对一

不同点：

(1)顺序表存储结构是顺序存储，内存当中存储不连续的链表是链式存储，通过指针将节点联系到一起，内存上存储不连续

(2)顺序表(数组)长度固定，链表不固定

(3)顺序表查找方便，但是插入和删除麻烦，链表插入和删除方便，但是查找麻烦

4.线性表的特征是什么？

线性表： 顺序表 链表 栈(顺序栈和链式栈) 队列(顺序队列也叫循环队列和链式队列)

线性表的特征：一对一，每个节点最多有一个前驱和一个后继（首尾节点除外）

五、队列

1、定义

只允许在两端进行插入和删除操作的线性表，在队尾插入，在队头删除 插入的一端，被称为"队尾"，删除的一端被称为"队头"

在队列操作过程中，为了提高效率，以调整指针代替队列元素的移动，并将数组作为循环队列的操作空间。

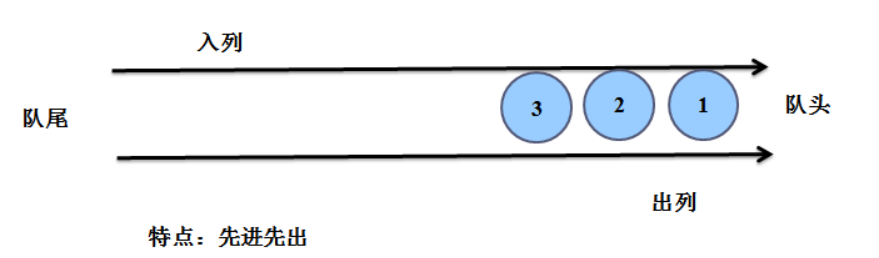
2、特点

先进先出 FIFO first in first out

后进后出 LILO last in last out

3、顺序队列（循环队列）

1）逻辑结构：线性结构

2）存储结构：顺序存储

3）操作：入队、出队

结构体：

#define N 5

typedef int datatype;

typedef struct

{

        datatype data[N];

        int rear;                 // 后面，队尾

        int front;                 // 前面，队头

} sequeue_t;         //sequence 顺序 queue队列

头文件：

#include <stdio.h>
#include <stdlib.h>
#define N 5
typedef int datatype;
typedef struct
{
	datatype data[N];//循环队列的数组
	int rear;//存数据端 rear 后面
	int front;//取数据端 front 前面
}sequeue_t;
//1.创建一个空的队列
sequeue_t *CreateEmptySequeue();
//2.入列 data代表入列的数据
int InSequeue(sequeue_t *p,datatype data);
//3.判断队列是否为满
int IsFullSequeue(sequeue_t *p);
//4.判断队列是否为空
int IsEmptySequeue(sequeue_t *p);
//5.出列 
datatype OutSequeue(sequeue_t *p);
//6.求队列的长度
int LengthSequeue(sequeue_t *p);
//7.清空队列函数
void ClearSequeue(sequeue_t *p);

3.1 创建一个空的队列

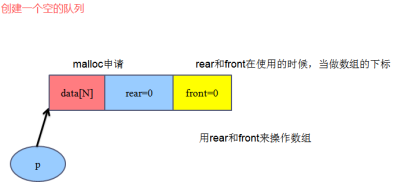
/*=============1.创建一个空的队列============*/
sequeue_t *CreateEmptySequeue()
{
    // 1.创建一个结构体大小的空间
    sequeue_t *p = (sequeue_t *)malloc(sizeof(sequeue_t));
    // 2.判断是否创建成功
    if (p == NULL)
    {
        perror("CreateEmptySequeue error");
        return NULL;
    }
    // 3.对结构体成员进行初始化
    p->front = 0;
    p->rear = 0;
    // 4.返回开辟空间的首地址
    return p;
}

3.2 入列 + 判满

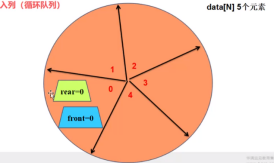
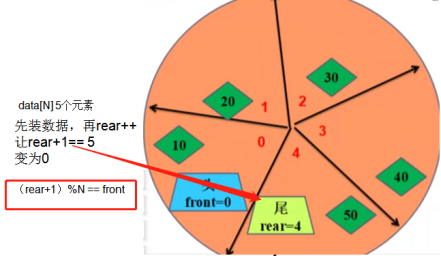
/*=============3.判断队列是否为满=============*/
int IsFullSequeue(sequeue_t *p)
{
    // 判断尾巴的下一个位置是否为头。是的话返回1，不是返回0
    return (p->rear + 1) % N == p->front;
}/*=============2.入列 data代表入列的数据============*/
int InSequeue(sequeue_t *p,datatype data)
{
    // 1.判满
    if (IsFullSequeue(p))
    {
        perror("InSequeue error");
        return -1;
    }
    // 2.数据入队
    p->data[p->rear] = data;
    // 3.尾巴移动
    p->rear = (p->rear + 1) % N;
    return 0;
}

3.3 出列 + 判空

/*=============4.判断队列是否为空============*/
int IsEmptySequeue(sequeue_t *p)
{
    return p->front == p->rear;
}/*=============5.出列============*/
datatype OutSequeue(sequeue_t *p)
{
    // 1.判空
    if (IsEmptySequeue(p))
    {
        perror("OutSequeue error");
        return -1;
    }
    // 2.取数据
    datatype temp = p->data[p->front];
    // 3.移动队头
    p->front = (p->front + 1) % N;
    // 4.返回数据
    return temp;
}

3.4 求队列长度

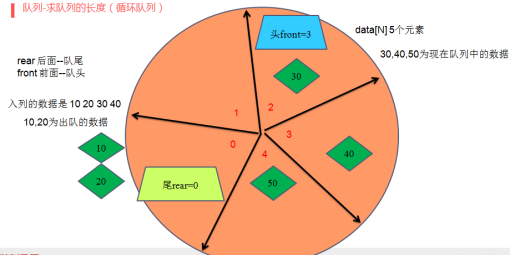
/*=============6.求队列的长度============*/
int LengthSequeue(sequeue_t *p)
{
    /*方法一*/
    // if (p->rear >= p->front)    /*尾大于头*/
    //     return p->rear - p->front;
    // else
    //     return p->rear - p->front + N;  /*尾小于头*/
    /*方法二*/
    return (p->rear - p->front + N) % N;
}

3.5 清空队列

/*=============7.清空队列函数============*/
void ClearSequeue(sequeue_t *p)
{
    p->front = p->rear; 
}

3.6 总结

循环队列中，假设数组的元素个数为N，那么循环队列中存储最多的数据个数为N-1个

原因：思想上，舍去数组上的一个存储位置,用于判断队列是否为满，先判断rear的下一个位置是否等于front return (p->rear+1) % N == p->front;

求长度：return (p->rear - p->front + N) % N;

4、链式队列（有头链表）

结构体：

typedef int datatype;

typedef struct node

{

        datatype data; //数据域

        struct node *next; //指针域

}  linkqueue_node_t,*linkqueue_list_t;

typedef struct         //将队列头指针和尾指针封装到一个结构体里

{

        linkqueue_list_t front; //相当于队列的头指针

        linkqueue_list_t rear; //相当于队列的尾指针

        //有了链表的头指针和尾指针，那么我们就可以操作这个链表

}  linkqueue_t;

头文件：

#include <stdio.h>
#include <stdlib.h>
typedef int datatype;
typedef struct node
{
	datatype data;//数据域
	struct node *next;//指针域
}linkqueue_node_t,*linkqueue_list_t;//linkqueue_list_t p == linkqueue_node_t *
typedef struct//将队列头指针和尾指针封装到一个结构体里
{
	linkqueue_list_t front;//相当于队列的头指针
	linkqueue_list_t rear;//相当于队列的尾指针
	//有了链表的头指针和尾指针，那么我们就可以操作这个链表
}linkqueue_t;
//1.创建一个空的队列
linkqueue_t *CreateEmptyLinkQueue();
//2.入列 data代表入列的数据
int InLinkQueue(linkqueue_t *p,datatype data);
//3.出列 
datatype OutLinkQueue(linkqueue_t *p);
//4.判断队列是否为空
int IsEmptyLinkQueue(linkqueue_t *p);
//5.求队列长度的函数
int LengthLinkQueue(linkqueue_t *p);
//6.清空队列
void ClearLinkQueue(linkqueue_t *p);

4.1 创建一个空队列

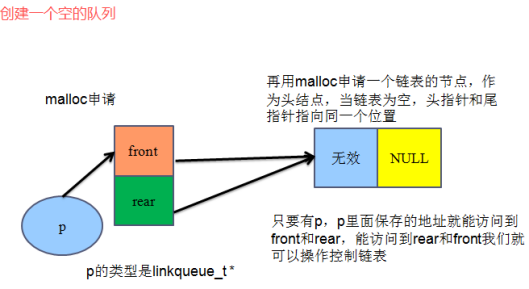
#include"linkqueue.h"
/*==============1.创建一个空的队列==============*/
linkqueue_t *CreateEmptyLinkQueue()
{
    // 1.开辟一个存放头尾指针结构体大小的空间
    linkqueue_t *p = (linkqueue_t *)malloc(sizeof(linkqueue_t));
    if (p == NULL)
    {
        perror("linkqueue_t malloc error");
        return NULL;
    }
    // 2.头尾指针初始化
    p->front = (linkqueue_list_t)malloc(sizeof(linkqueue_node_t));
    if (p->front == NULL)
    {
        perror("linkqueue_list_t malloc error");
        free(p);
        p = NULL;
        return NULL;
    }
    p->rear = p->front;
    // 3.头节点初始化
    p->front->next = NULL;
    return p;
}

4.2 入列

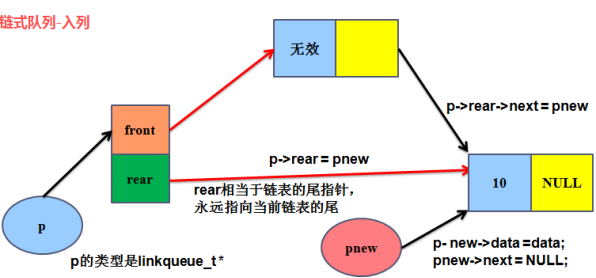
/*==============2.入列 data代表入列的数据==============*/
int InLinkQueue(linkqueue_t *p,datatype data)
{
    // 1.创建一个新的节点结构体类型的节点
    linkqueue_list_t pnew = (linkqueue_list_t)malloc(sizeof(linkqueue_node_t));
    if (pnew == NULL)
    {
        perror("InLinkQueue error");
        return -1;
    }
    // 2.对新节点初始化（数据域和指针域）
    pnew->data = data;
    pnew->next = NULL;
    // 3.将节点入队（尾插）
    p->rear->next = pnew;
    // 4.移动指向队尾的指针
    p->rear = pnew;
    return 0;
}

4.3 出列

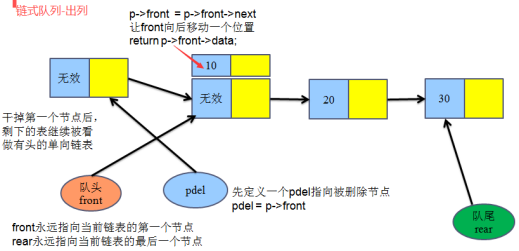
/*==============4.判断队列是否为空==============*/
int IsEmptyLinkQueue(linkqueue_t *p)
{
    // 如果是空的话返回1，非空返回0
    return p->front == p->rear;
}
/*==============3.出列 ==============*/
datatype OutLinkQueue(linkqueue_t *p)
{
    // 1.判空
    if (IsEmptyLinkQueue(p))
    {
        perror("OutLinkQueue error");
        return -1;
    }   
    // 2.定义一个pdel指向头节点
    linkqueue_list_t pdel = p->front;
    // 3.移动头指针到pdel位置
    p->front = pdel->next;
    // 4.释放头节点
    free(pdel);
    pdel = NULL;
    // 5.出队数据
    return p->front->data;
}

4.4 计算队列长度

/*==============5.求队列长度的函数 ==============*/
int LengthLinkQueue(linkqueue_t *p)
{
    int len = 0;
    linkqueue_list_t temp = p->front;
    while (temp != p->rear)
    {
        len++;
        temp = temp->next;
    }
    return len;
}

4.5 清空队列

/*==============6.清空队列 ==============*/
void ClearLinkQueue(linkqueue_t *p)
{
    while (p->front != p->rear)
        OutLinkQueue(p);
}

4.6 主函数

#include"linkqueue.h"
int main(int argc, char const *argv[])
{
    linkqueue_t *p = CreateEmptyLinkQueue();
    for(int i = 1; i < 6; i++)
        InLinkQueue(p, i);
    printf("len is %d\n", LengthLinkQueue(p));
    for(int i = 1; i < 6; i++)
        printf("%d ", OutLinkQueue(p)); 
    putchar(10);
    printf("len is %d\n", LengthLinkQueue(p));    
    return 0;
}​​​​​​​
http://www.dtcms.com/a/336732.html

相关文章：

  • 蓝桥杯C++
  • 下降路径最小和
  • 《Java高并发核心编程》笔记汇总
  • 【Java企业级开发】（八）Spring框架中Web项目构建
  • 【高等数学】第九章 多元函数微分法及其应用——第六节 多元函数微分学的几何应用
  • Transformer架构的数学本质：从注意力机制到大模型时代的技术内核
  • AI 编程在老项目中的困境与改进方向
  • 负载测试与压力测试详解
  • MySQL黑盒子研究工具 strace
  • 基于因果性的深层语义知识图谱对文本预处理的积极影响
  • Perf使用详解
  • AI系统性思维复盘概述
  • 【FreeRTOS】事件组
  • 电力设备状态监测与健康管理：从数据感知到智能决策的技术实践​
  • 通达信【牛股妖股埋伏】副图+选股指标
  • 报错注入原理与全方法总结
  • HAL-ADC配置
  • 快速了解均值滤波处理
  • 关于动态代理的个人记录
  • CF2121B Above the Clouds
  • 【Java】多线程Thread类
  • 什么是AIGC（人工智能生成内容）
  • 牛客周赛 Round 104(小红的树不动点)
  • 人工智能入门②：AI基础知识（下）
  • 计算机程序编程软件开发设计之node..js语言开发的基于Vue框架的选课管理系统的设计与实现、基于express框架的在线选课系统的设计与实现
  • STM32——软硬件I2C
  • Font Awesome Kit 使用详解
  • OTA升级
  • Vue Router 嵌套路由与布局系统详解：从新手到精通
  • 【牛客刷题】随机加减操作：两种高效解法详解（DFS记忆化搜索和动态规划集合更新法）