使用马尔可夫链如何解码、预测股市模式

文章出自：How Markov Chains Can Decode Stock Market Patterns。本篇文章适合对股市分析感兴趣的读者，尤其是新手。文章的亮点在于通过马尔可夫链模型，简单明了地展示了如何利用当前市场状态预测未来走势，并提供了实用的转移矩阵和稳态分布概念。这种方法适用于需要分析市场行为、制定投资策略的场景，例如预测股市短期波动或识别市场的自然平衡状态。
在实际案例中，作者通过Python示例展示了如何构建和应用这一模型，为投资者提供了数据驱动的决策支持。

---

---

马尔可夫链如何解码股市模式

我们都听过这句话：“过往表现不代表未来结果。” 这句话出现在每个金融免责声明中是有充分理由的。然而……交易员们仍在寻找模式，希望能破解市场行为的密码。

但是，如果市场确实有记忆，只是一个非常_短暂_的记忆呢？

马尔可夫链登场了。

1. 什么是马尔可夫链？

马尔可夫链的核心是一个数学系统，它根据某些概率规则从一个状态转换到另一个状态。其决定性特征是：下一个状态仅取决于当前状态，而不取决于之前事件的序列。

可以这样想……

想象一下天气。如果今天晴朗，明天有 80% 的概率保持晴朗，20% 的概率下雨。如果今天下雨，明天可能有 30% 的概率放晴，70% 的概率继续下雨。

关键在于：明天的天气只关心今天的天气，而不关心上周或上个月发生了什么。

2. 理解转移矩阵

我刚才描述的概率可以用所谓的转移矩阵来表示：

	到：晴朗	到：下雨
从：晴朗	0.8	0.2
从：下雨	0.3	0.7

这个矩阵非常强大，因为它完整地定义了我们的马尔可夫链。每一行代表当前状态，每一列代表可能的下一个状态，每个单元格显示该转换的概率。

3. 用矩阵乘法预测序列

真正有趣的地方来了……如果我们想预测的不是明天，而是两天后，甚至一周后的天气呢？

我们可以用矩阵乘法来实现！

假设今天晴朗，我们想知道后天的概率分布。我们将转移矩阵乘以自身：

	到：晴朗	到：下雨
从：晴朗	0.8	0.2
从：下雨	0.3	0.7

×

	到：晴朗	到：下雨
从：晴朗	0.8	0.2
从：下雨	0.3	0.7

=

	到：晴朗	到：下雨
从：晴朗	[0.70]	[0.30]
从：下雨	[0.45]	[0.55]

看这个新矩阵，如果今天晴朗，两天后有 70% 的概率晴朗，30% 的概率下雨。

这些数字是怎么来的？

• 晴朗→晴朗→晴朗的概率：[0.8 \times 0.8 = 0.64]
• 晴朗→下雨→晴朗的概率：[0.2 \times 0.3 = 0.06]
• 两天后晴朗的总概率：[0.64 + 0.06 = 0.70]

三天后，我们会再次将矩阵乘以自身。对于 n 天后，我们将矩阵提高到 n 次方。

4. 稳态的魔力

随着 [n] 变大，一些显著的事情发生了……矩阵会收敛到一个稳态，其中概率分布不再改变。让我们看看如果我们继续这个过程会发生什么：

经过 5 次迭代 ([P^5]):

	到：晴朗	到：下雨
从：晴朗	0.6027	0.3973
从：下雨	0.5960	0.4040

经过 10 次迭代 ([P^{10}]):

	到：晴朗	到：下雨
从：晴朗	0.6001	0.3999
从：下雨	0.6001	0.3999

这揭示了一个深刻的道理：无论我们从晴天还是雨天开始，经过足够长的时间，任何给定一天是晴天的概率都趋近于 60%，下雨的概率趋近于 40%。

这被称为马尔可夫链的_平稳分布_。它代表了系统的长期均衡，发生的原因是该过程逐渐“忘记”了其起点。初始状态的影响随着每次转换而减弱，直到变得无关紧要。

这表明股票市场具有自然的均衡状态。无论我们是从牛市还是熊市开始，状态的分布最终都可能收敛到可预测的模式。这可以通过揭示特定市场的“自然节奏”来为长期投资策略提供信息。

听起来和市场有时表现的方式很相似吗？

5. “无记忆性”市场假说

股票市场是出了名的复杂系统，受无数变量影响——经济指标、地缘政治事件、投资者心理等等。但是，如果日复一日，市场的下一步行动主要受其当前状态影响呢？

这就是马尔可夫链提供了一个引人入胜的视角。

6. 分解市场状态

要将马尔可夫链应用于股票市场，我们需要定义我们的“状态”。这些状态可以是：

• 大跌 (↓↓)
• 小跌 (↓)
• 中性 (→)
• 小涨 (↑)
• 大涨 (↑↑)

每天，市场都处于这些状态中的一个。马尔可夫模型随后计算从当前状态转换到明天每个可能状态的概率。

7. 转移矩阵：您的市场水晶球？

任何马尔可夫链的核心都是其转移矩阵——一个显示从任何状态到其他状态的概率的表格。

例如：

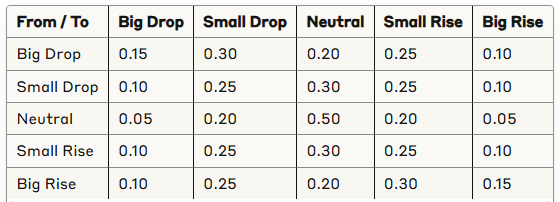
阅读这个矩阵很简单。如果今天“大跌”，那么明天有 15% 的概率也会“大跌”，30% 的概率“小跌”，依此类推……

8. 构建您自己的市场马尔可夫模型：分步指南

让我们一步一步地介绍如何使用 Python 实现股票市场分析的马尔可夫链模型：

8.1. 步骤 1：设置您的环境

首先，安装必要的库：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

8.2. 步骤 2：定义您的状态

第一个关键任务是将连续的价格变动转换为离散状态：

def create_states(prices, n_states=5):"""Convert continuous price changes into discrete states"""percent_change = prices.pct_change().dropna()try:if len(np.unique(percent_change.values)) < n_states:states = pd.cut(percent_change.values, bins=n_states,labels=range(n_states), duplicates='drop')else:states = pd.qcut(percent_change.values, q=n_states,labels=range(n_states), duplicates='drop')except ValueError:states = pd.cut(percent_change.values, bins=n_states,labels=range(n_states), duplicates='drop')return pd.Series(states, index=percent_change.index).astype(int)

这个函数完成了将连续百分比变化转换为离散状态的关键工作。它足够灵活，可以将数据分成 n_states 个箱，其中每个箱大致包含相同数量的观测值。

• 示例（5 个状态）：
  • 状态 0 (大跌)：最差的 20% 的日子
  • 状态 1 (小跌)：接下来的 20%
  • 状态 2 (中性)：中间的 20%
  • 状态 3 (小涨)：接下来的 20%
  • 状态 4 (大涨)：最好的 20% 的日子

8.3. 步骤 3：构建转移矩阵

1. 输入验证

if states.empty or len(states) < 2: return np.full((n_states, n_states), np.nan)

• 检查输入是否为空或太短以至于无法计算转换
• 如果输入无效，则返回一个填充 NaN 的矩阵

2. 初始化矩阵

matrix = np.zeros((n_states, n_states))

• 创建一个 [n_states \times n_states] 的零矩阵

• 例如，对于 [n_states=5]：

  [[0. 0. 0. 0. 0.][0. 0. 0. 0. 0.][0. 0. 0. 0. 0.][0. 0. 0. 0. 0.][0. 0. 0. 0. 0.]]
  

3. 计数转换

for (i, j) in zip(states[:-1], states[1:]):if pd.notna(i) and pd.notna(j): matrix[int(i)][int(j)] += 1

• 遍历连续的状态对（当前状态 i，下一个状态 j）

• 增加相应的矩阵单元格

• 计数后的示例结果：

  [[5. 2. 0. 0. 1.][1. 3. 2. 0. 0.][0. 1. 4. 1. 0.][0. 0. 3. 2. 1.][1. 0. 0. 1. 3.]]
  

  示例用法

  假设我们有这 10 天的状态：
  [0, 1, 1, 2, 1, 0, 2, 2, 1, 3]

  转换对将是：

  1. 0 → 1
  2. 1 → 1
  3. 1 → 2
  4. 2 → 1
  5. 1 → 0
  6. 0 → 2
  7. 2 → 2
  8. 2 → 1
  9. 1 → 3

  原始计数矩阵（转换为概率之前）将是：

  从/到	0	1	2	3
  0	[[0, 1, 1, 0]] (0→1 和 0→2)
  1	[1, 1, 1, 1]] (1→0, 1→1, 1→2, 1→3)
  2	[0, 2, 1, 0]] (2→1 两次, 2→2 一次)
  3	[0, 0, 0, 0]] (没有从 3 的转换)

4. 计算概率

row_sums = matrix.sum(axis=1, keepdims=True)
return np.divide(matrix, row_sums, out=np.zeros_like(matrix), where=(row_sums != 0))

• row_sums：计算从每个状态的总转换次数（每行的总和）

• keepdims=True 保持 2D 形状以便广播

• np.divide：通过将每行除以其总和来将计数转换为概率

• out=np.zeros_like(matrix)：如果无法执行除法，则返回零

• where=(row_sums != 0)：仅对非零行执行除法

  示例

  转换计数矩阵（原始）

  	下一个状态
  	0
  从 0	[[2, 5, 1, 0, 0],
  1	[1, 3, 2, 1, 0],
  2	[0, 2, 4, 2, 0],
  3	[0, 0, 3, 3, 1],
  4	[1, 0, 0, 2, 4]]

  转换为概率矩阵

  1. 计算行和（从每个状态的总转换次数）：

     • 第 0 行: [2+5+1+0+0 = 8]
     • 第 1 行: [1+3+2+1+0 = 7]
     • 第 2 行: [0+2+4+2+0 = 8]
     • 第 3 行: [0+0+3+3+1 = 7]
     • 第 4 行: [1+0+0+2+4 = 7]

  2. 将每个计数除以其行和：

     • 每个单元格变为：计数 / 行和

  	下一个状态
  	0
  从 0	[0.25, 0.63, 0.12, 0.00, 0.00],
  1	[0.14, 0.43, 0.29, 0.14, 0.00],
  2	[0.00, 0.25, 0.50, 0.25, 0.00],
  3	[0.00, 0.00, 0.43, 0.43, 0.14],
  4	[0.14, 0.00, 0.00, 0.29, 0.57]

9. 步骤 4：整合所有部分

以下是如何使用这些函数处理真实股票数据：

data = load_data_from_source("TICKER_SYMBOL")
prices = data['Close']state_labels = ["Big Drop", "Small Drop", "Neutral", "Small Rise", "Big Rise"]
n_states = len(state_labels)states_series = create_states(prices, n_states=n_states)trans_matrix = build_transition_matrix(states_series, n_states=n_states)current_state_idx = states_series.iloc[-1]
current_state = state_labels[current_state_idx]print(f"Current State: {current_state}")
print("\nNext State Probabilities:")
for i, state in enumerate(state_labels):print(f"- {state}: {trans_matrix[current_state_idx][i]:.2%}")

10. 步骤 6：可视化结果

可视化有助于解释结果：

def plot_transition_matrix(matrix, labels):"""Create a heatmap of the transition matrix"""plt.figure(figsize=(10, 8))sns.heatmap(matrix, annot=True, cmap="YlGnBu", fmt=".2f",xticklabels=labels, yticklabels=labels, cbar=True, vmin=0, vmax=1)plt.title("Transition Probability Matrix")plt.xlabel("Next State")plt.ylabel("Current State")plt.tight_layout()plt.show()

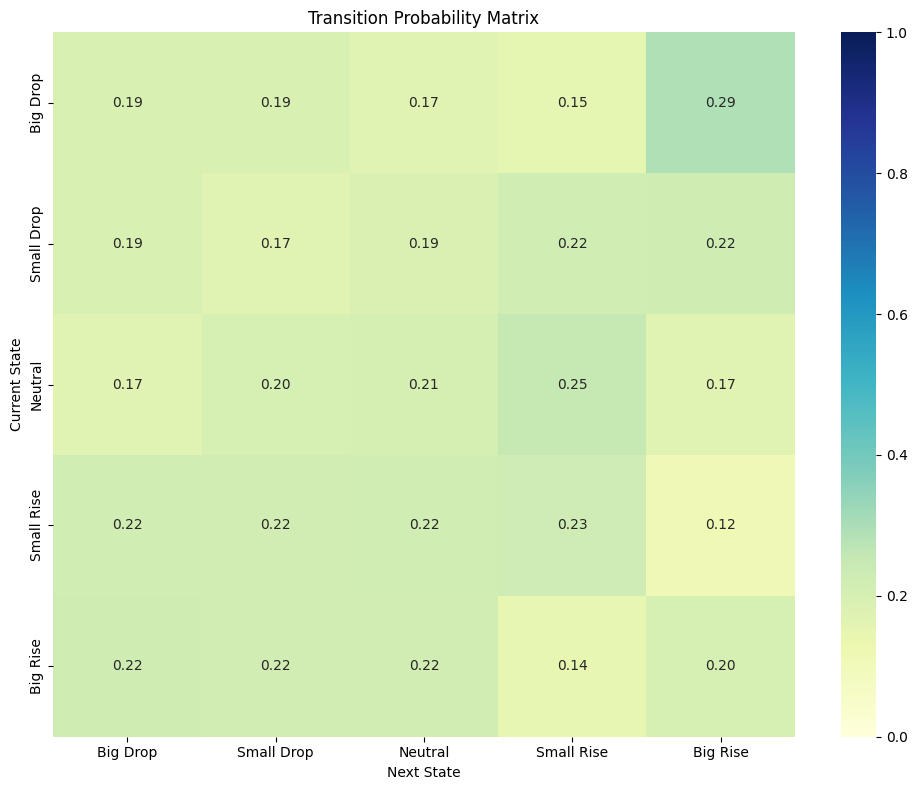
11. 步骤 7：长期预测

要查看市场随时间趋于平衡的位置（稳态）：

def compute_steady_state(trans_matrix, iterations=20):"""Compute the steady state by matrix power iteration"""current_matrix = trans_matrix.copy()for _ in range(iterations):current_matrix = np.dot(current_matrix, trans_matrix)return current_matrix[0]

steady_state = compute_steady_state(trans_matrix)print("Long-term Market State Distribution:")
for state, prob in zip(state_labels, steady_state):print(f"- {state}: {prob:.2%}")

结果：
长期市场状态分布（稳态）：

• 大跌 : 19.99%
• 小跌 : 19.99%
• 中性 : 19.99%
• 小涨 : 19.99%
• 大涨 : 20.06%

12. 解释真实市场数据：案例研究

让我们看一个真实的例子，了解它在实践中是如何运作的：

当前市场状态（截至 2025-05-06）：

• 价格：$9.18
• 日变化：-1.40%
• 状态：大跌
  转移矩阵（下一个状态的概率）：

	下一个大跌	下一个小跌	下一个中性	下一个小涨	下一个大涨
大跌	0.1940	0.1940	0.1679	0.1530	0.2910
小跌	0.1940	0.1716	0.1903	0.2201	0.2239
中性	0.1679	0.2015	0.2052	0.2537	0.1716
小涨	0.2201	0.2164	0.2201	0.2276	0.1157
大涨	0.2230	0.2156	0.2156	0.1450	0.2007

下一个状态概率（鉴于当前 = 大跌）：

• 大跌 : 19.40%
• 小跌 : 19.40%
• 中性 : 16.79%
• 小涨 : 15.30%
• 大涨 : 29.10%

这告诉我们什么？让我们分解一下……

1. 当前情况：该股票收盘价为 9.18 美元，较前一天下跌 1.40%，我们的模型将其归类为“大跌”状态。
2. 转移矩阵：此表显示了从任何状态（行）移动到任何其他状态（列）的历史概率。
3. 次日预测：由于我们目前处于“大跌”状态，我们查看矩阵的第一行。有趣的是，概率分布表明，在大跌之后，最有可能的下一个状态实际上是……大涨（29.10%）！

该模型给出的是概率，而不是二元预测。虽然有近 30% 的概率大涨，但也有约 39% 的综合概率继续负向波动（大跌 + 小跌）。

这种平衡的视角有助于投资者设定切合实际的预期，并相应地调整头寸规模或对冲策略。虽然不能保证，但这些概率为决策提供了数据驱动的框架。

13. 但是……它有效吗？

有趣的地方来了。马尔可夫链不声称能精确预测明天的股价——那将是金融巫术。相反，它们为我们理解市场行为提供了一个概率框架。

真正的价值在于：

1. 风险评估 — 根据当前情况了解极端波动的可能性
2. 模式识别 — 识别市场是“正常”行为还是异常行为
3. 策略开发 — 创建考虑状态相关行为的交易系统

14. 局限性（保持现实）

在您辞去日常工作成为马尔可夫驱动的交易奇才之前，让我们承认一些局限性：

• 市场不断演变，其转移概率也会发生变化
• 外部冲击，如疫情，可能会使历史模式失效
• 状态和时间范围的选择会显著影响结果
• “无记忆性”特性对于复杂的市场动态来说可能过于简化

15. 您的下一步

好奇想自己尝试一下吗？以下是入门方法：

1. 收集您喜欢的股票或指数的历史价格数据
2. 定义有意义的状态（基于百分比变化或其他标准）
3. 计算您的转移矩阵
4. 测试模型是否为您的特定投资目标提供了有用的见解

我准备了一个完整的 Google Colab 工作示例，您可以进行实验：Markov Chain Stock Market Analysis

该笔记本包含所需的所有代码，用于：

• 定义您自己的马尔可夫状态
• 从历史价格数据构建转移矩阵
• 可视化结果
• 根据当前市场状态进行概率预测