当前位置：首页 > news >正文

风电功率预测实战：从数据清洗到时空建模

news 2025/8/15 8:36:04

基于KDD Cup 2022冠军数据集与轻量级神经网络

一、问题背景与数据价值

风电功率预测（Wind Power Forecasting, WPF）是电网稳定的核心技术。参考论文《SDWPF: A Dataset for Spatial Dynamic Wind Power Forecasting》：

"风电的波动性对电网接入构成重大挑战... 高精度预测是保障供电安全的关键"

论文提出的SDWPF数据集首次融合风机空间位置（134台风机的x/y坐标）与动态工况（温度、叶片角度等），突破了传统时序预测的局限。

二、数据预处理实战

步骤1：关键风机筛选

# 选择40号风机数据（代码DOC3）
filtered_df = df[df['TurbID'] == 40]  # 从134台风机中聚焦单点

步骤2：数据清洗

删除全特征缺失行（共15,231行→15,231行无缺失）
异常值处理：依据论文规则自动标记无效数据

# 论文定义的无效数据规则（PDF1 Section 4.1）
invalid_cond1 = (Patv <= 0) & (Wspd > 2.5)  # 有风速无功率
invalid_cond2 = (Prab > 89)                  # 叶片角度异常

步骤3：特征工程

通过Spearman热力图发现核心相关特征：

import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties# 计算相关系数
corr_matrix = x.corr(method='spearman')# 绘制热力图
plt.figure(figsize=(10, 8))
sns.heatmap(corr_matrix, annot=True, cmap='RdYlBu', vmin=-1, vmax=1, annot_kws={"size": 8, "ha": 'center'}, fmt='.2f')
plt.title('相关性热力图')# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体为黑体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题plt.xticks(rotation=90)
plt.yticks(rotation=0)
# plt.show()
# # 保存图像
plt.savefig('spearman-heatmap.png',dpi=300, bbox_inches='tight')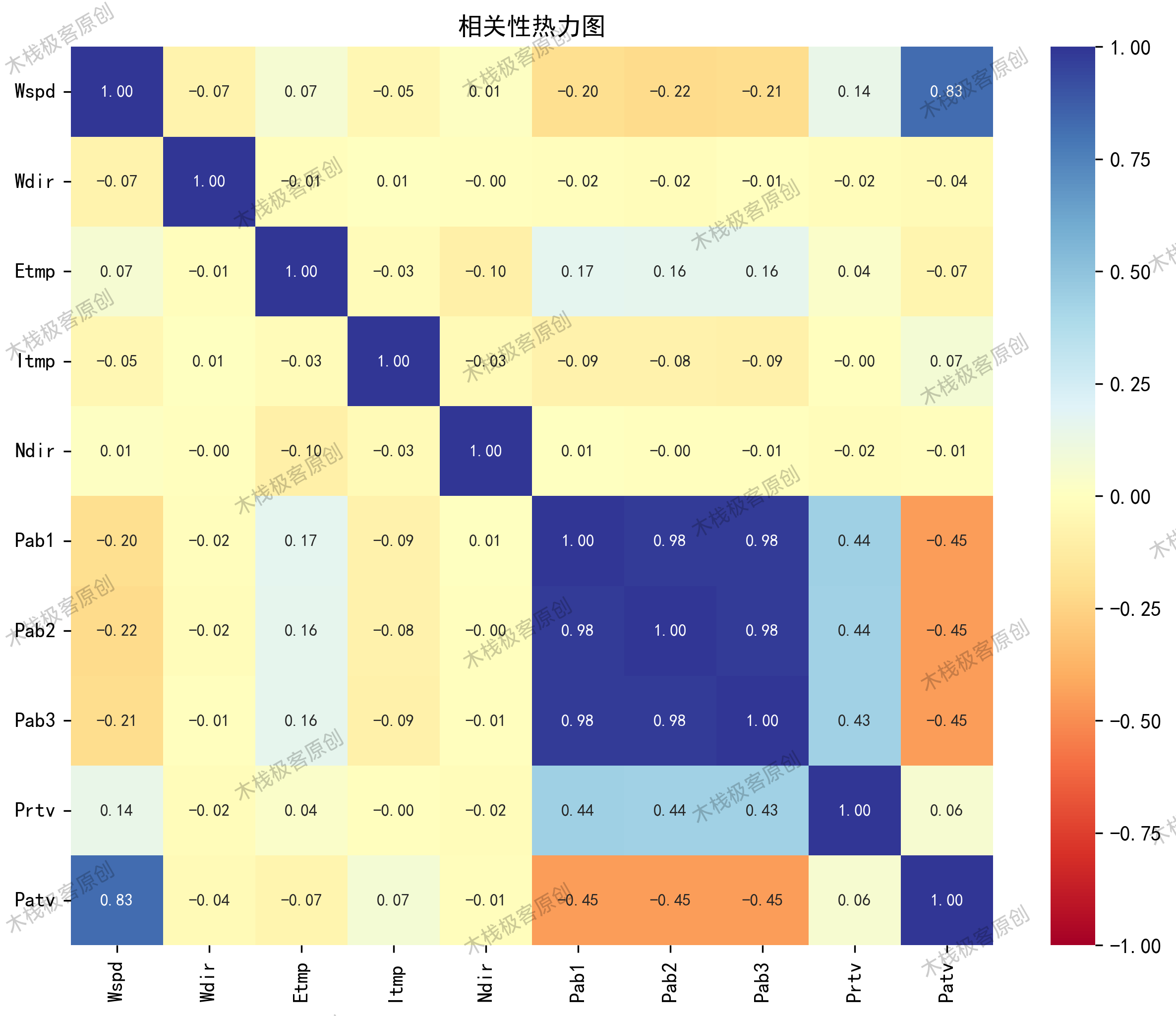

使用热力图的方式对结果进行可视化，如图所示。按照相关性从大到小排列为：Wspd：0.825326、Pab3：0.452152、Pab1：0.450817、Pab2：0.449813、Itmp：0.072295、Etmp：0.066919、Prtv：0.059205、Wdir：0.037463、Ndir：0.013293。结果解释：当|r|>0.95时，变量间存在显著性相关；当0.95>|r|>0.8时，变量间高度相关；当0.8>|r|>0.5时，变量间中度相关；当0.5>|r|>0.3时，变量间低度相关；当|r|<0.3时，变量间关系极弱，认为不相关。因此，采取r>0.3的列作为后续模型的输入特征，即Wspd、Pab3、Pab1、Pab2四列。

三、轻量级神经网络建模

3.1 数据归一化和划分数据集

# 读取CSV文件
TurbID40 = pd.read_csv('TurbID40_clean.csv')# 划分特征和目标变量
x = TurbID40[['Wspd', 'Pab3', 'Pab1', 'Pab2']]
y = TurbID40['Patv']# 划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)# 数据归一化
scaler = MinMaxScaler()
x_train_scaled = scaler.fit_transform(x_train)
x_test_scaled = scaler.transform(x_test)
y_train_scaled = scaler.fit_transform(y_train.values.reshape(-1, 1))
y_test_scaled = scaler.transform(y_test.values.reshape(-1, 1))

3.2 模型架构对比

神经网络被广泛应用于各种预测任务。本报告使用两个常见的神经网络模型，分别为：前馈神经网络 (Feedforward Neural Networks)：也称为多层感知器 (Multilayer Perceptrons, MLP)，是最基本的神经网络类型。它们由多个神经元层组成，信息单向传递，通常用于解决分类和回归问题。卷积神经网络 (Convolutional Neural Networks, CNN)：主要用于处理图像和视觉数据，CNN 在处理非图形数据时，可以将数据视为具有类似网格结构的形式。

MLP（多层感知器）的一般结构为：输入层、多个隐藏层和输出层。

CNN（卷积神经网络）的一般结构为：输入层、卷积层、激活函数层、池化层、全连接层和输出层。由于处理的数据非图像数据，因此，CNN不使用池化层。

模型类型	输入层	隐藏层	输出层	特点
MLP	4节点 (Dense)	64→32→16 (ReLU激活)	1节点	全连接
CNN	4节点	Conv2D(32内核)+Flatten	1节点	空间特征提取

# MLP构建代码
mlp_model = Sequential([Dense(64, activation='relu', input_shape=(4,)),Dense(32, activation='relu'),Dense(16, activation='relu'),Dense(1)
])# 构建 CNN 模型
cnn_model = keras.Sequential([layers.Reshape((2, 2, 1), input_shape=(4,)),layers.Conv2D(32, kernel_size=(2, 2), activation='relu'),layers.Flatten(),layers.Dense(16, activation='relu'),layers.Dense(1)
])

3.3 模型实验结果

3.4 参数优化实验

在构建神经网络模型时，设置节点数和层数，需要根据问题的复杂性、数据集的特征和实验结果进行调整。节点数的选择是一个经验性的过程，并没有固定的规则，通常需要进行多次实验来找到最佳的节点数。

在设置节点数时，有几个常见的考虑因素：

问题复杂性：如果问题非常复杂，可能需要更多的节点来捕捉输入数据中的复杂模式和关系。增加节点数可以增加模型的容量和拟合能力，但也可能导致过拟合。因此，在增加节点数时要注意避免过度拟合。

数据集的特征：数据集的特征分布和维度也会影响节点数的选择。如果数据集具有复杂的特征和关系，可能需要更多的节点来捕捉这些特征。另外，如果输入数据的维度较高，可能需要更多的节点来处理高维特征空间。

实验和验证：在构建模型时，通常需要进行实验和验证来评估不同节点数下模型的性能。可以尝试不同的节点数，然后使用验证集评估模型的性能指标，如损失函数、准确率、R2 等。根据验证集的性能，选择最佳的节点数。

输入层节点，由于输入4个特征，因此输入层为4个节点且固定不动。其余层数和节点均自行进行调整，使用数据做实验进行验证，由于数据集并非较复杂的数据，因此，采用较简单参数进行逐步实验，各个模型参数和实验结果如图所示。根据下述实验结果可知，随着模型层数和节点的增加，模型复杂度上升的同时，准确率在提升，RMSE也在下降，表示模型更好。最终确定模型结果为R2为0.98和0.99，所以不再继续增加模型复杂度。