第1节 从函数到神经网络:AI思路的逆袭之路
🤔 开篇灵魂拷问
是不是觉得AI知识体系庞大到吓人?看了一堆快餐视频还是云里雾里?别慌!这个系列就是要帮你打通任督二脉,用"既快又慢、既深入又肤浅、既有趣又严肃"的方式讲透AI基础知识!
💡 核心信念:万物皆函数
记住!整个AI的出发点就一句话:世界上所有逻辑和知识都能用函数(function)表示。把现实抽象成符号,设置运算规则(函数),算出来结果再反推现实——听着是不是特有道理?
事实上函数就是一种变换,对数据进行变换得到我们所需要的结果。

🔍 早期AI的"理想主义":符号主义
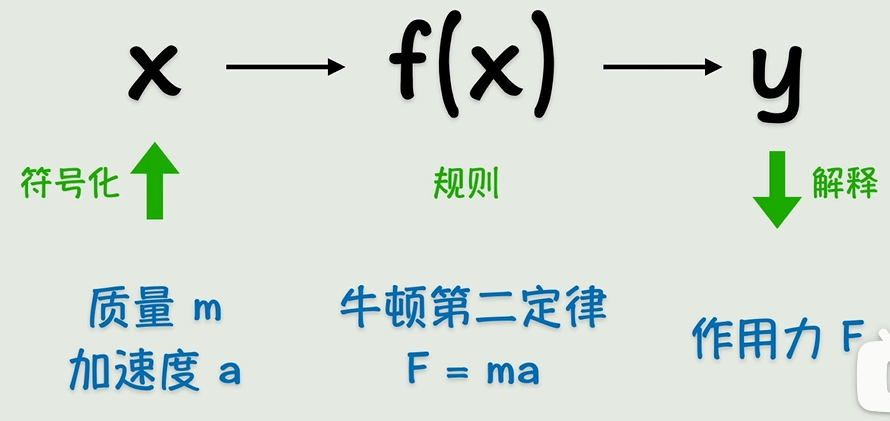
早期的人工智能->符号主义,即用精确的函数来表示一切。
直角三角形求斜边用勾股定理(a²+b²=c²),物体受力用F=ma——这些明确规则的函数玩得转,但遇到图片识别猫狗这种人类觉得简单到爆炸的问题,直接变成史诗级难题!连语法明确的语言翻译都做不到丝滑,更别说复杂的人类智能了...只能说,早期AI还是太年轻,把世界想得太简单!
摆烂式创新:联结主义登场
找不到精确函数咋办?人类终于承认自己"太菜了",发明了猜+简化的骚操作!比如给一堆X和Y的数据,先瞎猜个函数(比如Y=X),然后慢慢调参数(W和B)让它贴近真实数据,就算不能完全吻合,差不多就行!这就是现代AI的核心思路——联结主义!
但是很多时候,我们没办法找到一个精确的函数来描述某个关系,(图中计算机很难识别)
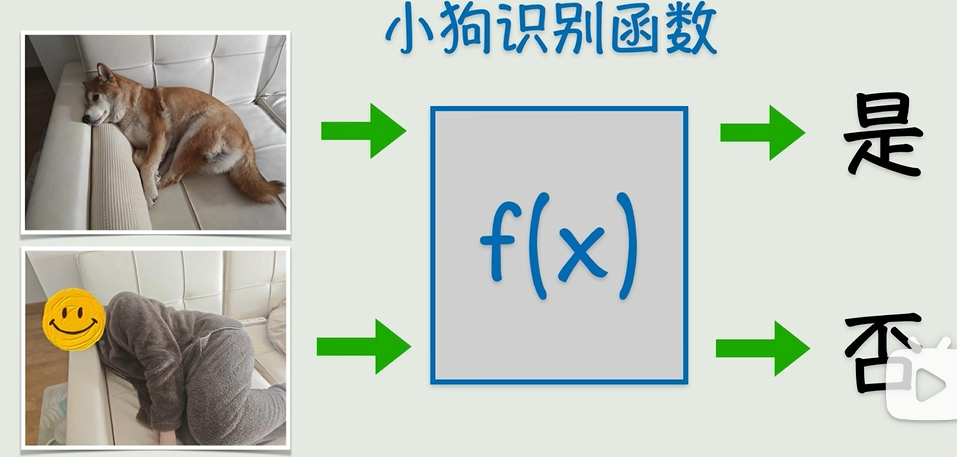
退而求其次选择一个近似解也不错,也就是说函数没必要精确的通过每一个点,它只需要最接近结果就好了,这就是联结主义。
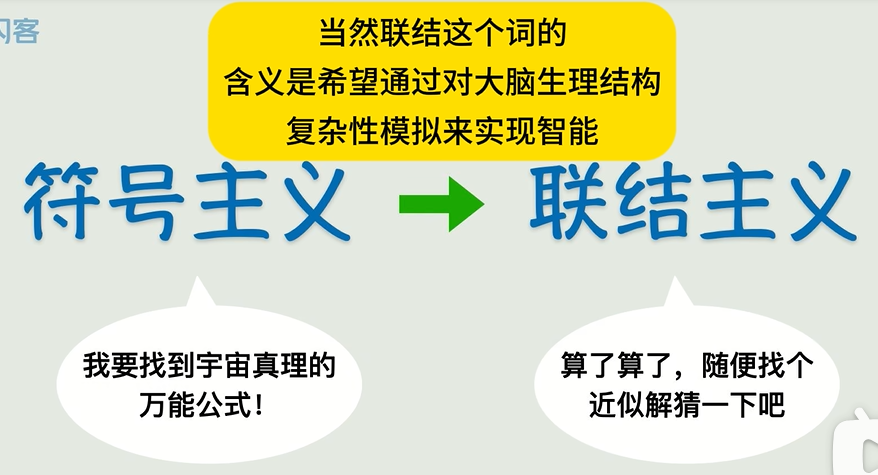
🚀 连接主义的逆袭
你还别不信!就靠这种"连蒙带猜"的方法,用很少参数就能实现手写数字识别,直接打脸当初看不起它的专家!事实证明:结果说话才是硬道理!
虽然“连蒙带猜”听起来不靠谱,但实战效果惊人:用很少的参数就能实现手写数字识别等任务,证明了有效性后才被重视。

当数据稍微变化一下,出现曲线的时候,简单的线性函数就没办法解决这个问题了。那我们的目标就是将线性函数转为非线性函数,这可以通过套一个非线性函数来做到,比如平方、正弦函数、指数函数。
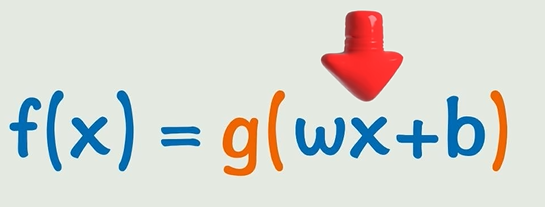
这就是激活函数。激活函数把原来的线性关系转变成非线性的关系。
激活函数:给直线“掰弯”的魔法
线性函数(y=wx+b)太死板,遇到非线性数据就不行。于是给线性变换套个非线性激活函数(如平方、sin、e^x),让曲线“弯得更灵活”。

🧠 神经网络进化论
线性函数不够用?给它套个非线性"马甲"!比如加个平方、sin函数——这就是激活函数,瞬间让函数从"死板直线"变身"灵活曲线"!
一层不够就叠罗汉!线性变换+激活函数反复套娃,中间藏起来的"黑箱子"叫隐藏层,输入层→隐藏层→输出层的信号传播就是前向传播。理论上,这玩意儿能逼近任意复杂的连续函数!

这还不够,正常情况下我们不会只有一个输入,并且只有一个激活函数可能不会达到理想的结果,所以开始嵌套!

像这样多个输入,激活函数外面加一次线性变换,再套一个激活函数,并且还可以不断嵌套。通过这样的方式,我们可以构造出非常复杂的关系,理论上可以逼近任意的连续函数。
但这样看起来太复杂了,所以我们引入神经元的概念,
神经网络:函数套娃的可视化
- 把“线性变换+激活函数”画成神经元(小圈圈),输入层→隐藏层→输出层,每层都是一次函数变换。
- 隐藏层:中间层不直接输出,相当于“套在函数里的函数”,让模型能表达更复杂关系。
- 前向传播:信号从输入层到输出层的计算过程,本质就是分步算一个超复杂函数的值。

图中的一个小圈就是一个神经元,多个神经元互相连接形成的网状结构就叫做神经网络。同时我们可以看到随着函数式子的嵌套,神经网络也在拓展,原本的输出成为了隐藏层:位于输入层和输出层之间的中间层。隐藏层的主要作用是对输入数据进行复杂的特征提取和变换,
核心洞察:神经网络理论上可以逼近任意连续函数,而整个AI的后续知识,本质上都是为了算出这些神经元之间的w(权重)和b(偏置)!
🎯 终极目标:猜中W和B
不管神经网络多花里胡哨,本质都是为了猜出所有参数(W权重和B偏置)!从简单的直线方程到上万神经元的深度网络,AI工程师每天都在跟这些参数死磕...至于怎么磕?卖个关子,且听下回分解!
从神经网络的图示来看,就像是一个信号从左向右传播的过程,这个过程就叫做神经网络的前向传播。并且神经网络的层数和每一层的神经元都可以叠加,这样就可以构成一个非常复杂的非线性函数。看起来复杂,但是我们的目标还是一开始说的:找到一个近似解,也就是根据已知的x、y猜出所有的w和b。

