LeeCode 46. 全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1] 输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1] 输出:[[1]]
提示:
1 <= nums.length <= 6-10 <= nums[i] <= 10nums中的所有整数 互不相同
答案:
static int getArrangeCount(int n) { // n个不同的数,全排列方法数,为 n * (n - 1) * ... * 1if (n == 1)return 1;return n * getArrangeCount(n - 1);
}/**
* arr为其中的一个排列。
* currIdx标识当前要确认的哪个索引的数
*/
static void pailie(int** res, int totalSize, int* currCount, int* nums, int* arr, int arrSize, int currIdx, int* used) {//printf("totalSize: %d, *currCount:%d, currIdx: %d\n", totalSize, *currCount, currIdx);if (*currCount == totalSize) {// 说明全部任务完成了printf("all finish 实际没调用到这一行\n");return;}if (currIdx == arrSize) {//printf("一个排列准备好了\n");// 一个排列准备好了// 复制一个数组出来,原始数组还有用,后面需要回溯尝试其他排列方案int* arr_ = (int*)malloc(arrSize * sizeof(int));if (!arr_) return;memcpy(arr_, arr, arrSize * sizeof(int));//printf("打印一个排列:");//printArr(arr_, arrSize);//printf("*currCount: %d\n", (*currCount));*(res + *currCount) = arr_; // 保存结果*currCount = *currCount + 1;//printf("new *currCount: %d\n", (*currCount));return;}//printf("currIdx: %d\n", currIdx);for (int i = 0; i < arrSize; i++) {if (used[nums[i] + 10]) {// 已使用过该数//printf("已使用过%d\n", nums[i]);continue;}//printf("没使用过%d\n", nums[i]);arr[currIdx] = nums[i]; // 使用这个数//printf("arr[%d] = %d\n", currIdx, nums[i]);used[nums[i] + 10] = 1; // 标识这个数用过了//printf("nums[0] used: %d, nums[1] used:%d, nums[2] used:%d\n", used[nums[0] + 10], used[nums[1] + 10], used[nums[2] + 10]);// 再确认下一位pailie(res, totalSize, currCount, nums, arr, arrSize, currIdx + 1, used);// 回溯,即回退,不使用该数字。然后会尝试使用其他数字used[nums[i] + 10] = 0;//printf("回退后:");//printf("nums[0] used: %d, nums[1] used:%d, nums[2] used:%d\n", used[nums[0] + 10], used[nums[1] + 10], used[nums[2] + 10]);}
}/*** Return an array of arrays of size *returnSize.* The sizes of the arrays are returned as *returnColumnSizes array.* Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().*/
int** permute(int* nums, int numsSize, int* returnSize, int** returnColumnSizes) { // LeeCode46 全排列int count = getArrangeCount(numsSize); // 全排列方法数*returnSize = count;*returnColumnSizes = (int*)malloc(count * sizeof(int));if (*returnColumnSizes == NULL) {return NULL;}for (int i = 0; i < count; i++) {*(*returnColumnSizes + i) = numsSize; // 返回的每个数组的长度都为numsSize}int** res = (int**)malloc(count * sizeof(int*));if (!res) return NULL;int* arr = (int*)malloc(numsSize * sizeof(int));if (!arr) return NULL;// 根据题意, nums 中的所有整数 互不相同, 且-10 <= nums[i] <= 10. 所以排列数字的时候使用used数组标识哪些数已使用过了// used[0]标识-10是否使用过。 userd[20]标识10是否使用过int used[21] = { 0 };int currCount = 0;pailie(res, count, &currCount, nums, arr, numsSize, 0, used);free(arr); // 这个临时数组不需要了,释放内存return res;
}测试代码:
void printArr(int** arr, int size, int* returnColumnSizes) {printf("[");int isFirst = 1;for (int i = 0; i < size; i++) {if (isFirst) {isFirst = false;}else {printf(",");}int isSubFirst = 1;printf("[");for (int j = 0; j < returnColumnSizes[i]; j++) {if (isSubFirst) {isSubFirst = false;}else {printf(",");}printf("%d", arr[i][j]);}printf("]");}printf("]\n");
}void printArr(int* arr, int size)
{printf("[");int isFirst = 1;for (int i = 0; i < size; i++) {if (isFirst) {isFirst = false;}else {printf(",");}printf("%d", arr[i]);}printf("]\n");
}void testLeeCode46(void) { // LeeCode46全排列int nums[] = { 1, 2, 3 };int numsSize = 3;int returnSize; // 用于接受结果二维数组的长度。int* returnColumnSizes; // 用来接受结果二维数组的每个元素(即子数组)的长度int** res = permute(nums, numsSize, &returnSize, &returnColumnSizes);printArr(res, returnSize, returnColumnSizes);// 释放内存for (int i = 0; i < returnSize; i++) {free(res[i]);}free(res);free(returnColumnSizes);
}打印:
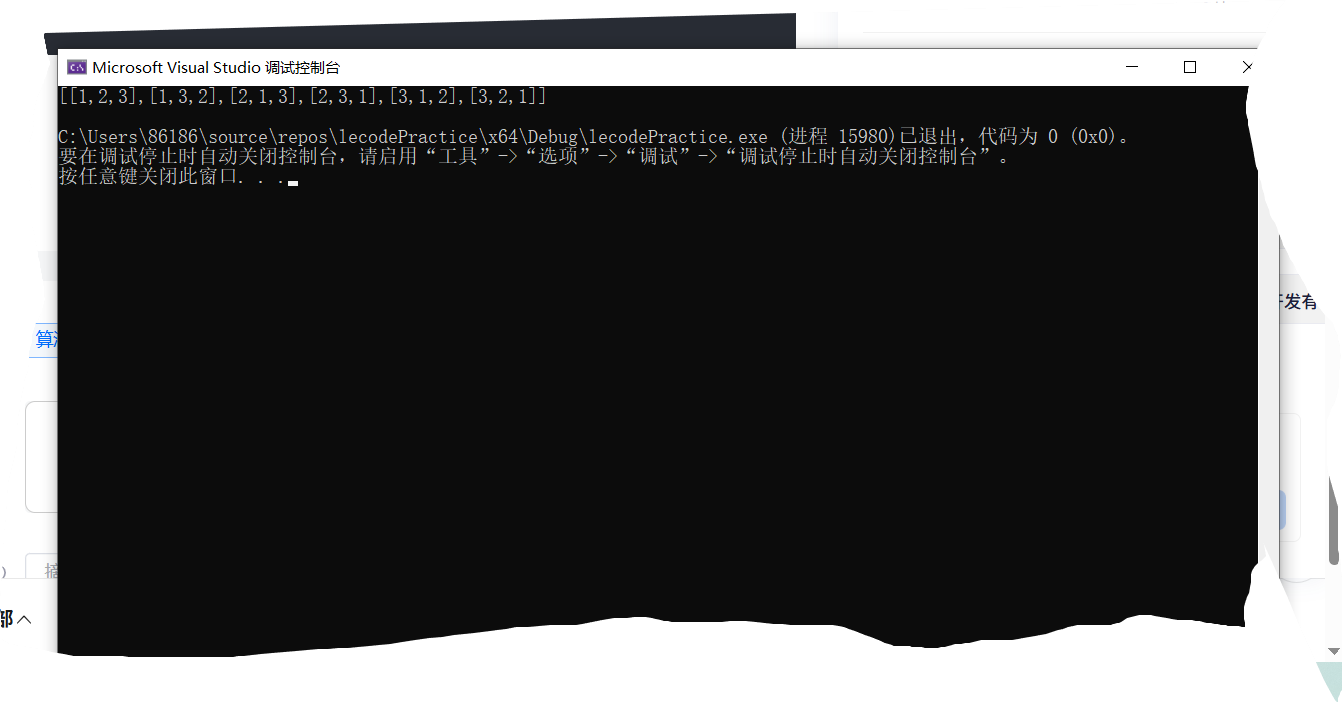
ok. 提交到LeeCode:
ok. 总结:使用的回溯算法(即深度优先算法)将所有的排列都穷举出来。
