数据结构---二叉树(概念、特点、分类、特性、读取顺序、例题)、gdb调试指令、时间复杂度(概念、大O符号法、分类)
一、二叉树
1、树
1)概念
树是 n(n >= 0) 个结点的有限集合。若 n=0 ,为空树。
在任意一个非空树中:
(1)有且仅有一个特定的根结点;
(2)当 n>1 时,其余结点可分为 m 个互不相交的有限集合T1、T2......Tm,其中每一个集合又是一个树,并且称为子树。
2)度、度数、深度
结点拥有子树的个数称为结点的度。度为 0 的结点称为叶结点;度不为 0 称为分支结点。
树的度数:指在这颗树中,最大的结点的度数,称为树的度数。
树的深度(高度):指从根开始,根为第一层,根的孩子为第二层,即树的层数,称为树的深度。
树的存储:顺序结构、链表结构。
2、二叉树(binary tree)
1)概念
二叉树是 n 个结点的有限集合,集合要么为空树,要么由一个根节点和两棵互不相交的树组成,这两棵树分别称为根节点的左子树和右子树。
2)特点
(1)每个结点最多两个子树。
(2)左子树和右子树是有顺序的,次序不能颠倒。
(3)如果某个结点只有一个子树,也要区分左、右子树。
3)特殊的二叉树
(1)斜树
斜树分为两种,一种是所有的结点都只有左子树,称为左斜树;另一种是所有的结点都只有右子树,称为右斜树。
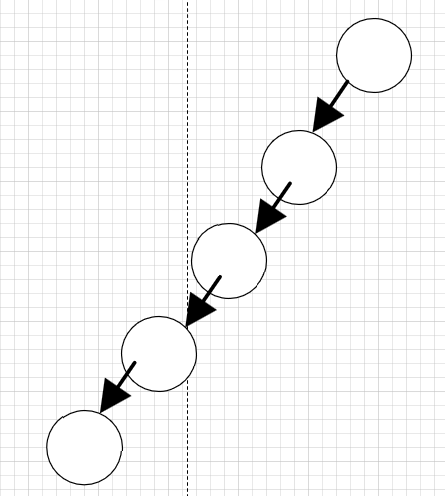
(2)满二叉树
满二叉树是指所有的分支结点都存在左右子树,并且叶子都在同一层上。
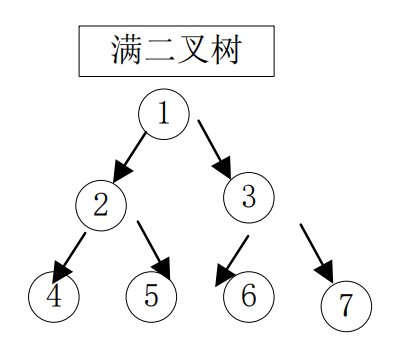
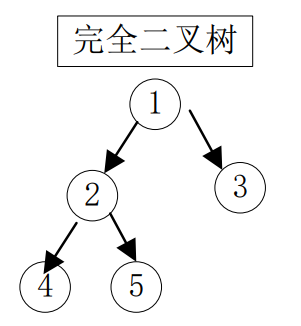
(3)完全二叉树
完全二叉树是指:对于一颗具有 n 个结点的二叉树按照层序编号,如果编号 i( 1<= i <= n )的结点于同样深度的满二叉树中编号为 i 的结点在二叉树中的位置完全相同,则此树称为完全二叉树。
4)特性
(1)在二叉树的第 i 层上最多有 2^(i-1) 个结点,i >= 1。
(2)深度为 k 的二叉树至多有 2^k-1 个结点,k >= 1。
(3)任意一个二叉树T,如果其叶子结点的个数为 N,度数为 M,则 N=M+1。
(4)有 n 个结点的完全二叉树深度为(logn / log2)+ 1。
5)层序
前序:根左右。先访问根结点,再访问左结点,最后访问右结点。
中序:左根右。先从根结点开始(不是先访问根结点),从左结点开始访问,再访问根结点,最后访问右结点。
后序:左右根。先从根结点开始(不是先访问根结点),从左结点开始访问,再访问右结点,最后访问根结点。
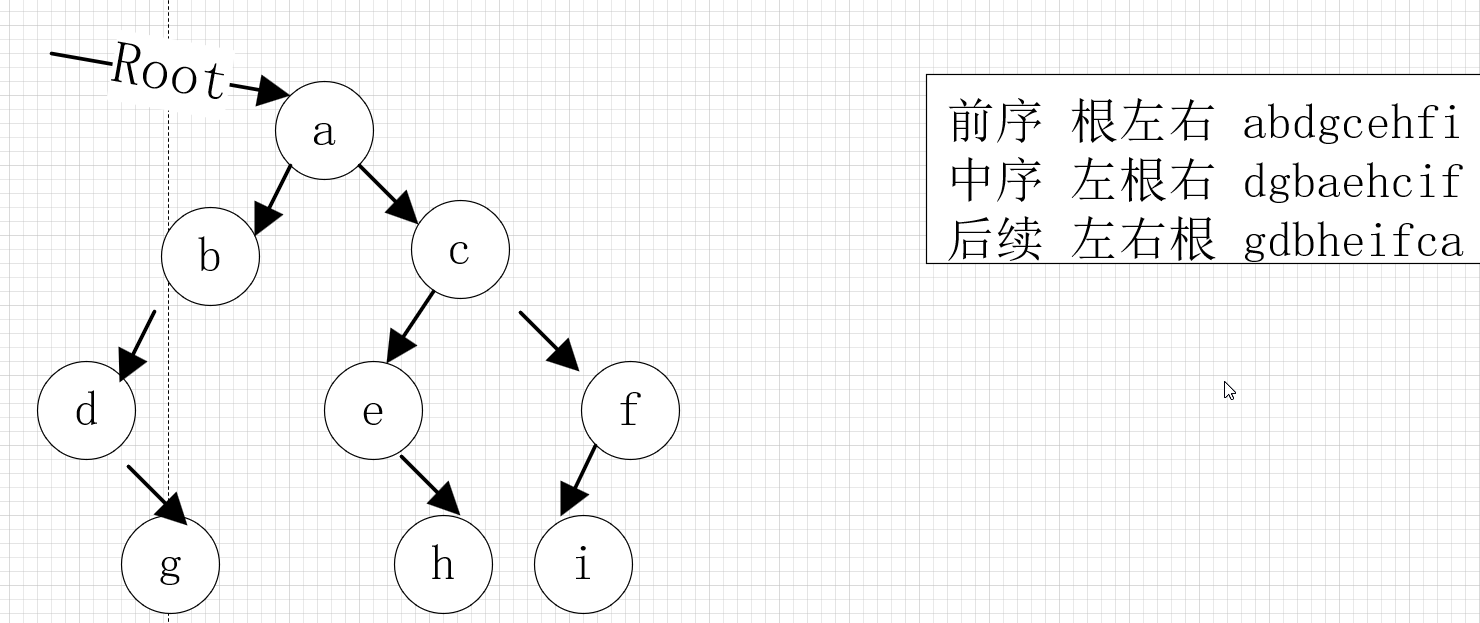
6)二叉树的函数应用
(1)创建二叉树函数
void CreateTree(BiTNode **root)
{char c = data[ind++];if('#' == c){*root = NULL;return ;}else{*root = malloc(sizeof(BiTNode));if(NULL == *root){printf("malloc error\n");*root = NULL;return ;}(*root) -> data = c;CreateTree(&(*root) -> ichild);CreateTree(&(*root) -> rchild);}return ;
}
( 2)根左右(前序)函数封装
//根左右
void PreOrderTraverse(BiTNode *root)
{if(NULL == root){return ;}else{printf("%c", root -> data);PreOrderTraverse(root -> ichild);PreOrderTraverse(root -> rchild);}return ;
}( 3)左根右(中序)函数封装
//左根右
void InOrderTraverse(BiTNode *root)
{if(NULL == root){return ;}InOrderTraverse(root -> ichild);printf("%c", root -> data);InOrderTraverse(root -> rchild);return ;
}(4)左右根(后序)函数封装
//左右根
void PostOrderTraverse(BiTNode *root)
{if(NULL == root){return ;}PostOrderTraverse(root -> ichild);PostOrderTraverse(root -> rchild);printf("%c", root -> data);return ;
}(5)二叉树销毁函数封装
//销毁
void DestroyTree(BiTNode *root)
{if(NULL == root){return ;}DestroyTree(root -> ichild);DestroyTree(root -> rchild);free(root);return ;
}( 6)头文件与其余声明
#include <stdio.h>
#include <string.h>
#include <stdlib.h>typedef char DATATYPE;typedef struct BiTNode
{DATATYPE data;struct BiTNode *ichild, *rchild;
}BiTNode;char data[] = "Abd#g###ce#h##fi###";
int ind = 0;
( 7)主函数运行格式
int main(int argc, char **argv)
{BiTNode *root;CreateTree(&root);PreOrderTraverse(root);printf("\n");InOrderTraverse(root);printf("\n");PostOrderTraverse(root);printf("\n");DestroyTree(root);root = NULL;return 0;
}
二、gbd调试指令
gdb 调试指令用来寻找段错误。
1、一般调试
1)gcc -g 文件名
2)gbd ./a.out (a.out 为该函数的可执行文件)
3)b 函数名 设置断点,运行到这个函数位置,程序自动暂停
b 数字 运行到 main函数的这一 “数字” 行,程序自动暂停
4)r 运行
5)n 执行下一步(行)步过,若是函数,直接调用结束
6)p 使用p命令,查看变量或指针等数据,p a(变量); p *a(指针)
2、其他相关命令
1)bt 与 where 显示栈结构,函数的调用关系
2)s 步入,如果是函数,进入函数
3)c 跳出循环,在循环后面设置断点,然后按 c 可返回调用处
4)display 和 p 相似,一直显示变量
5)q 退出 gbd 操作界面
三、各类排序算法的时间复杂度
1、概念
时间复杂度是衡量算法执行效率的重要指标,描述了算法的运行时间随输入规模(n)增长而变化的趋势,而非具体的运行时间。
2、推导大O阶方法
1)用常数 1 取代运行时间中的所有加法常数。
2)在修改后的运行次数函数中,只保留最高阶项。
3)如果最高阶项存在且不是 1 ,则去除与这个项相乘的常数。
得到的结构就是大O阶。
3、表示方法
采用大O符号(Big O Notation)来表示,忽略了常数项、低阶项和系数,只保留对增长趋势影响最大的项。例如下图:(图中 阶 代表时间复杂度)
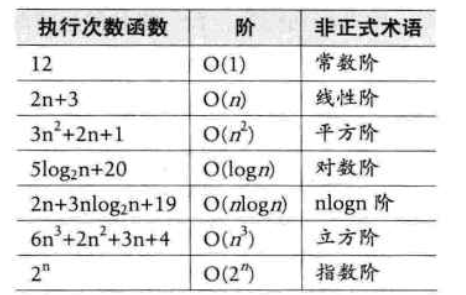
4、常见时间复杂度(按效率高到低排序)
1)常数阶 O(1)
算法执行时间不随规模 n 变化,始终为固定步骤,如访问数组中的某个元素。
2)对数阶 O(log n)
执行时间随 n 增长,但增长速度极慢(每步可将问题规模缩小一半),如二分查找。
3)线形阶 O(n)
执行时间与 n 成正比例增长,如线性查找。
4)线形对数阶 O(n log n)
效率介于 O(n) 和 O(n^2) 之间,常见于高效排序算法,如快速排序、归并排序。
5)平方阶 O(n^2)
执行时间与 n 的平方成正比,适用于小规模数据,如冒泡排序。
6)指数阶 O(2^n)、阶乘阶 O(n!)4
效率极低,随 n 增长,执行时间呈爆炸式增长,仅适用于极小规模数据。
5、各类算法时间复杂度整理
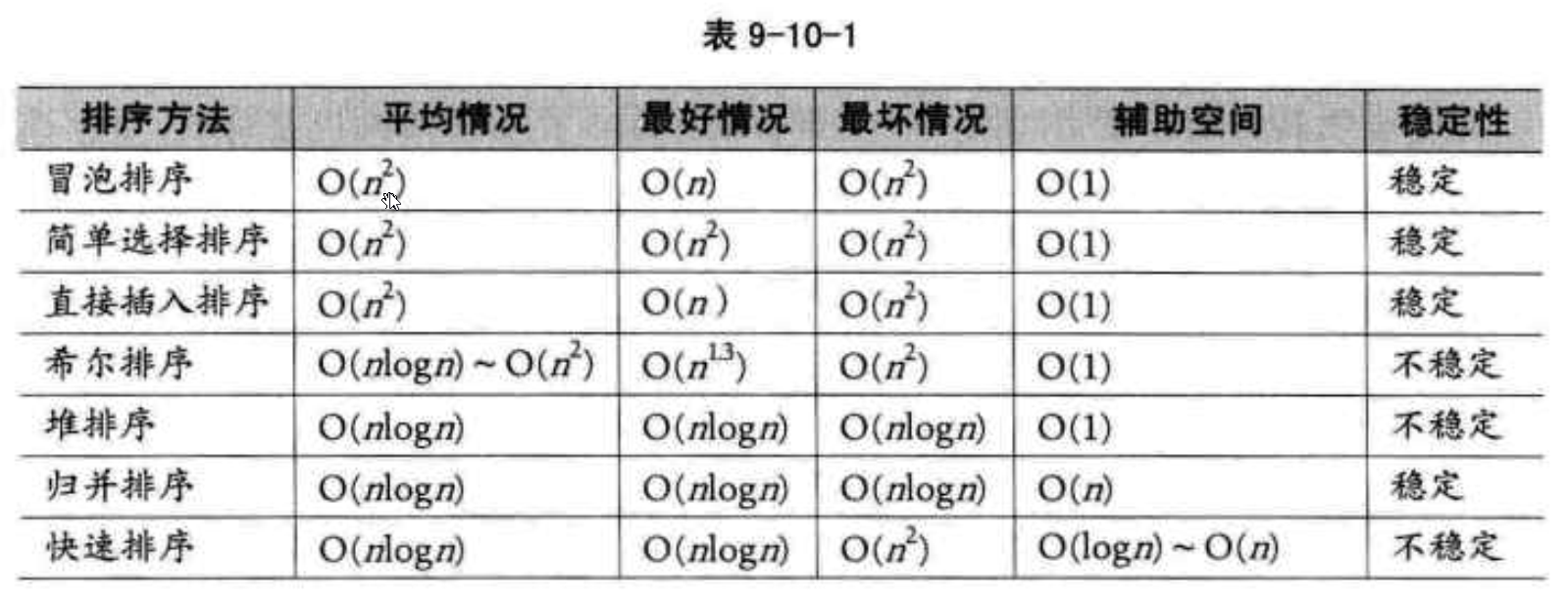
常用的时间复杂度所耗费的时间从小到大依次是:
![]()
【END】
