几个概率分布在机器学习应用示例

一、说明

在这份快速指南中，我们将介绍最重要的分布——从始终公平的均匀分布，到钟形的正态分布，计数点击的泊松分布，以及二元选择的二项分布。
没有复杂的数学，只有清晰的概念、真实的例子，以及为什么它们重要。

二、均匀分布

2.1 理论和实验

想象一下，你在一个自助餐上，有十盘完全相同的食品：意大利面、米饭、鸡肉、豆腐、沙拉等。每盘食物的量相同，份量也一样。没有哪一盘看起来更诱人，也没有哪道菜更丰富。你闭上眼睛随机指向一盘，那就是你的餐点。
关键要点：每道菜被选中的概率是相等的。没有偏见，没有口味优势。纯粹是均匀的机会。这就是概率论中均匀分布的概念。

均匀分布的图形是一个矩形：
• X轴：值从aaa到b
• Y轴：恒定高度[1/(b-a)]
在a和b之间的每个值具有相同的概率密度。

均匀分布的参数：
• a：下界（最小值）
• b：上界（最大值）
概率密度函数（PDF）：

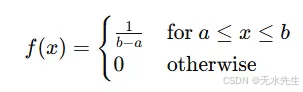
这表示在均匀分布图中平直线的高度，例如一块长度上厚度一致的巧克力棒。

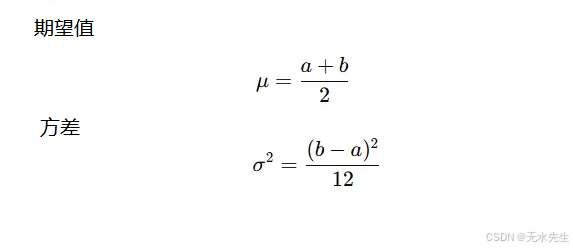
# Import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import uniform# Step 1: Define the parameters of the Uniform distribution
a = 2       # Lower bound of the distribution (start of the interval)
b = 8       # Upper bound of the distribution (end of the interval)# Step 2: Generate a range of x values to evaluate the PDF over
# We're adding a buffer of 1 unit on each side for better visualization
x = np.linspace(a - 1, b + 1, 1000)# Step 3: Compute the PDF values using scipy's uniform distribution
# The 'loc' parameter shifts the distribution to start at 'a'
# The 'scale' parameter is the width of the interval, i.e., (b - a)
pdf_values = uniform.pdf(x, loc=a, scale=b - a)# Step 4: Plotting the PDF
plt.figure(figsize=(10, 5))  # Set the size of the figure
plt.plot(x, pdf_values, label='PDF of Uniform({},{})'.format(a, b), color='darkblue', linewidth=2)# Step 5: Fill the area under the curve for visual clarity
plt.fill_between(x, pdf_values, alpha=0.3, color='skyblue')# Step 6: Add plot titles and axis labels
plt.title('Continuous Uniform Distribution: U({}, {})'.format(a, b), fontsize=14)
plt.xlabel('x (Random Variable)', fontsize=12)
plt.ylabel('Probability Density f(x)', fontsize=12)# Step 7: Display key features
plt.axvline(a, color='gray', linestyle='--', label='Lower Bound (a)')
plt.axvline(b, color='gray', linestyle='--', label='Upper Bound (b)')
plt.legend()
plt.grid(True)
plt.tight_layout()# Step 8: Show the plot
plt.show()

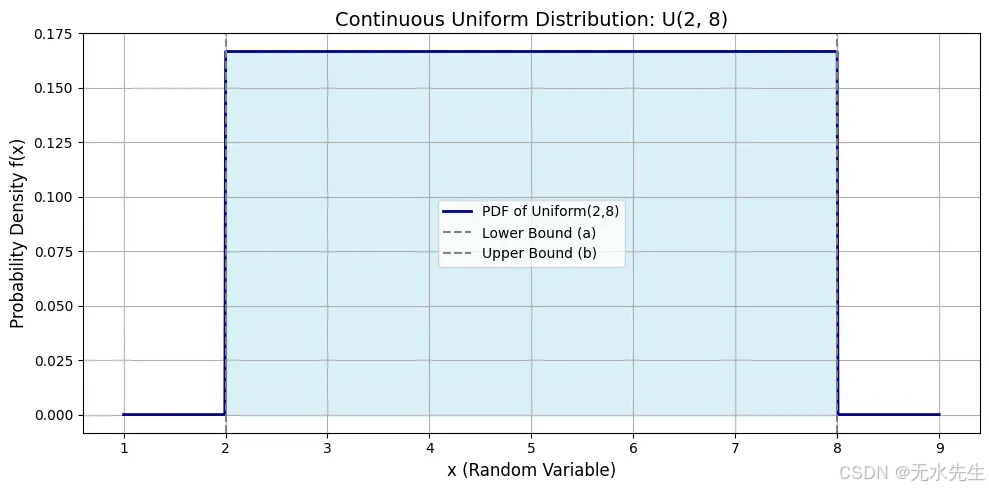
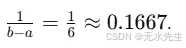
在a=2和b=8之间的曲线平坦顶部表明该范围内每个值的密度相同。平坦线的高度为0.1667。从2到8的曲线下阴影区域代表总概率等于1。
为什么均匀分布重要
• 随机性的基准：大多数随机数生成器从均匀分布开始。
• 模拟输入：在没有其他信息的情况下，假设均匀分布是最安全的方法。
• 公平性建模：在游戏、彩票和公平资源分配中。

2.2 应用在机器学习中

均匀分布就像我们呼吸的空气：无形但至关重要。它不作任何假设，因此在学习旅程的开始阶段以及希望实现公平性、中立性和探索性时，它是完美的选择。

1. 神经网络中的权重初始化
   在训练神经网络时，我们首先为模型的权重分配随机值。但是，选择这些随机值的方式很重要。
   均匀初始化通常被使用：
   
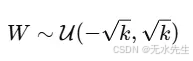
   确保每个权重从无偏开始，但保持在受控范围内。像TensorFlow、Keras和PyTorch这样的库提供了这一功能：
   为什么重要：
   • 避免权重更新中的对称性
   • 防止激活函数饱和
   • 在反向传播过程中保持梯度流动

torch.nn.init.uniform_(tensor, a=-0.05, b=0.05)

在进行交叉验证和实验时的随机抽样：当我们随机抽样时，
• 训练数据与测试数据
• 超参数值
• 自助重采样
如果没有先验知识，我们使用：
这确保了每个样本具有相同的概率，从而导致无偏实验。例如：

np.random.uniform(low=0, high=1, size=1000)

超参数调优和网格搜索：如果你不知道最佳的学习率、dropout率或正则化因子，均匀分布提供了一种中立且公平的方式来探索连续的超参数空间。

learning_rate = np.random.uniform(0.0001, 0.1)
#0.00677831298

三、正态分布：自然界的钟形曲线

3.1 理论和实验

按Enter键或点击以查看完整大小的图片

正态分布是建模不确定性和噪声以及自然和机器学习系统中平衡的黄金标准。它提醒我们，虽然异常值存在，但生活和数据中的大部分倾向于围绕“正常”轨道运行。想象一下你在一个纸杯蛋糕比赛中，1000名烘焙师提交他们的作品。大多数纸杯蛋糕都处于“平均”范围内，既不太甜也不太淡。有些太甜了，有些几乎没有味道。但大多数呢？刚刚好。
这就是正态分布——自然界平衡极端值与强烈中心的方式。在正态分布中，接近均值的值最为常见，而极端值（过高或过低）则较为罕见。它是对称的、钟形的，并且在统计学和机器学习中具有基础性地位。
为什么正态分布很重要？

正态分布的形状
• 它是一条钟形曲线。
• X轴：值的范围（例如，身高、体重、考试分数）
• Y轴：概率密度——该值出现的可能性。
大多数值集中在均值（μ）周围，随着远离均值，曲线对称地逐渐变窄。
正态分布的参数：
• μ：均值（曲线中心）
• σ：标准差（钟形曲线的扩展或宽度）
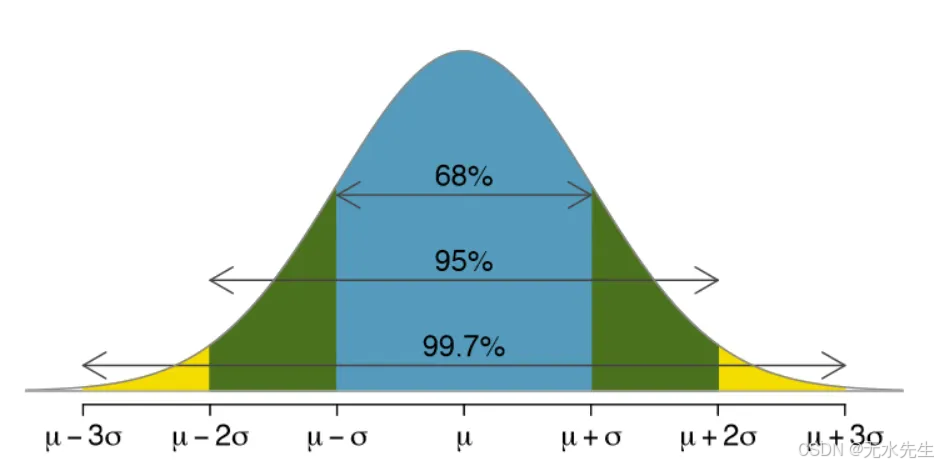
图表告诉我们什么？
• 最高点在均值处（这里，μ=0）。
• 68%的值位于一个标准差范围内（μ±σ）。
• 95%的值位于两个标准差范围内，99.7%的值位于三个标准差范围内（这被称为经验法则）。
概率密度函数（PDF）。
这是著名的钟形公式。指数项随着我们远离均值而降低曲线的高度。

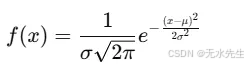
# Import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm# Define parameters for multiple distributions
# List of tuples, each containing (mu, sigma) for a distribution
distributions_params = [(0, 1),    # Standard Normal(2, 0.5),  # Shifted mean, smaller std dev(-1, 2),   # Shifted mean, larger std dev(0, 0.8)   # Same mean, slightly smaller std dev
]# Define a list of colors for plotting each distribution
colors = ['darkred', 'darkblue', 'darkgreen', 'purple']# Step 1: Generate a range of x values that covers all distributions
# Find the min and max bounds considering all mu and sigma values
min_mu = min([p[0] for p in distributions_params])
max_mu = max([p[0] for p in distributions_params])
max_sigma = max([p[1] for p in distributions_params])# Generate x values based on the most extreme mu and sigma to ensure coverage
x = np.linspace(min_mu - 4*max_sigma, max_mu + 4*max_sigma, 1000)# Step 2: Plot each distribution
plt.figure(figsize=(12, 7)) # Increased figure sizefor i, (mu, sigma) in enumerate(distributions_params):# Compute the PDF valuespdf_values = norm.pdf(x, loc=mu, scale=sigma)# Plot the PDF with a specific color and labelplt.plot(x, pdf_values, label=f'μ={mu}, σ={sigma}', color=colors[i], linewidth=2)# Optional: Fill the area under the curveplt.fill_between(x, pdf_values, alpha=0.2, color=colors[i])# Step 3: Annotate plot
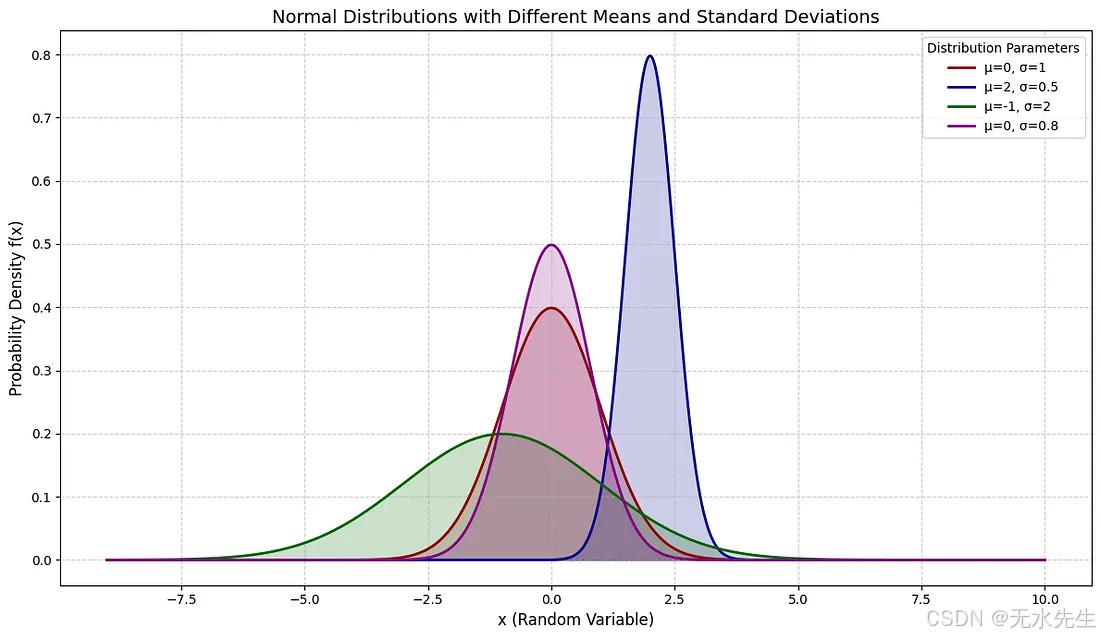
plt.title('Normal Distributions with Different Means and Standard Deviations', fontsize=14)
plt.xlabel('x (Random Variable)', fontsize=12)
plt.ylabel('Probability Density f(x)', fontsize=12)
plt.legend(title="Distribution Parameters")
plt.grid(True, linestyle='--', alpha=0.6)
plt.tight_layout()# Step 4: Show the plot
plt.show()

3.2 正态分布的机器学习应用

1. 特征分布假设
   许多机器学习算法假定输入特征服从正态分布：
   • 线性回归
   • 高斯朴素贝叶斯
   • 线性判别分析（LDA）
   如果数据不服从正态分布，性能可能会下降，这就是为什么我们要进行标准化或应用对数变换、Box-Cox变换等。
   在这个例子中，我们模拟了代表客户行为的偏斜数据，并拟合了一个线性回归模型来预测结果。原始数据遵循指数分布，这违反了许多模型的正态性假设。在对特征应用Yeo-Johnson变换使其正态化后，模型的表现显著提高，R²从0.85增加到0.91。这表明将偏斜数据转换为更接近正态分布的数据可以导致更准确的预测和更可靠的模型。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.preprocessing import PowerTransformer
from scipy.stats import norm# Simulate non-normal data (skewed exponential)
np.random.seed(42)
n_samples = 200
X = np.random.exponential(scale=2.0, size=(n_samples, 1))
y = 3 * np.log(X + 1).flatten() + np.random.normal(0, 0.5, size=n_samples)# Fit Linear Regression to original (non-normal) data
model_raw = LinearRegression().fit(X, y)
y_pred_raw = model_raw.predict(X)
r2_raw = r2_score(y, y_pred_raw)# Apply a Box-Cox-like transformation to normalize the feature
pt = PowerTransformer(method='yeo-johnson')
X_transformed = pt.fit_transform(X)# Fit Linear Regression to transformed data
model_trans = LinearRegression().fit(X_transformed, y)
y_pred_trans = model_trans.predict(X_transformed)
r2_trans = r2_score(y, y_pred_trans)# Plotting original vs transformed feature distribution
fig, axes = plt.subplots(1, 2, figsize=(12, 5))axes[0].hist(X, bins=30, color='skyblue', edgecolor='black', density=True)
x_vals = np.linspace(0, X.max(), 100)
axes[0].set_title('Original Feature Distribution (Skewed)')axes[1].hist(X_transformed, bins=30, color='salmon', edgecolor='black', density=True)
axes[1].set_title('Transformed Feature Distribution (Normalized)')plt.tight_layout()
plt.show()# Return R^2 scores to show performance difference
(r2_raw, r2_trans)
Press enter or click to view image in full size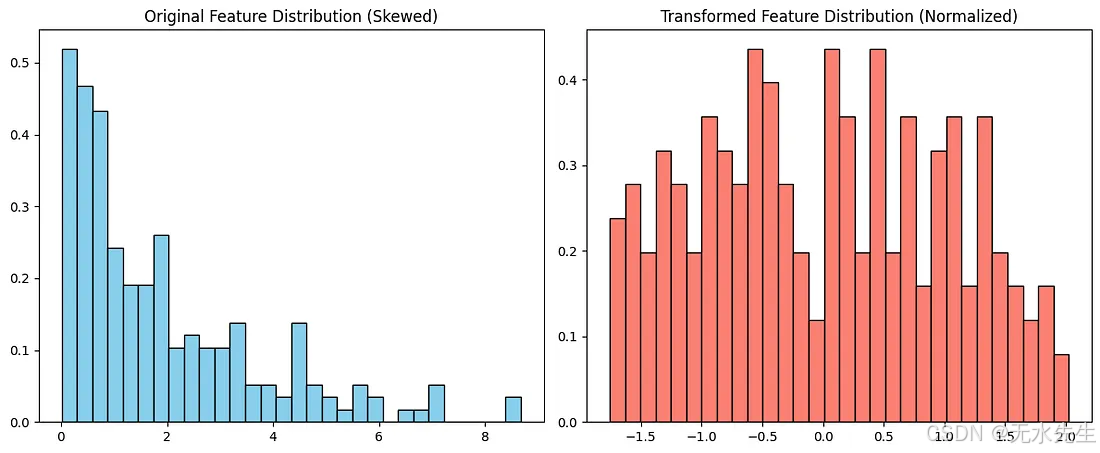

output (r2_raw, r2_trans): (0.85087454878016, 0.9124403892942448)

深度学习中的权重初始化
虽然均匀分布是标准选择，但正态（或高斯）初始化也被广泛使用：为什么？
• 保持激活值和梯度在合理范围内
• 帮助网络更高效、更稳定地训练。概率模型与推断
贝叶斯机器学习通常假设正态先验和正态似然。
示例：
• 高斯混合模型（GMMs）
• 变分自编码器（VAEs）
在VAEs中，潜在空间使用正态分布建模，允许平滑且可微的采样。
在高流量系统中，正常行为遵循钟形曲线，异常值则位于尾部。这非常适合用于：
• 信用卡欺诈检测
• 网络入侵检测
• 制造缺陷检测
在本示例中，我们模拟了1000笔围绕50美元的正常交易，标准差为5美元，这符合日常购买的情况。然后我们注入了几笔异常交易：80美元、85美元和90美元，代表潜在的欺诈行为。
我们使用三倍标准差规则：任何超过平均值三倍标准差的数据都会被标记为异常。在这种情况下，检测算法成功识别了注入的异常值以及一些自然但罕见的交易，如69美元或33美元。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm# Step 1: Simulate normal behavior (e.g., transaction amounts)
np.random.seed(42)
normal_data = np.random.normal(loc=50, scale=5, size=1000)  # average amount: $50# Step 2: Inject a few anomalies (fraudulent transactions)
anomalies = np.array([80, 85, 90])  # unusually high transaction amounts# Combine data
all_data = np.concatenate([normal_data, anomalies])# Step 3: Compute mean and standard deviation
mu = np.mean(normal_data)
sigma = np.std(normal_data)# Step 4: Identify anomalies using 3-sigma rule
threshold_high = mu + 3 * sigma
threshold_low = mu - 3 * sigma
detected_anomalies = all_data[(all_data > threshold_high) | (all_data < threshold_low)]# Step 5: Plot
plt.figure(figsize=(10, 5))
plt.hist(normal_data, bins=40, alpha=0.6, color='skyblue', edgecolor='black', label='Normal Transactions')
plt.axvline(threshold_high, color='red', linestyle='--', label='Upper Threshold (3σ)')
plt.axvline(threshold_low, color='red', linestyle='--', label='Lower Threshold (3σ)')
plt.scatter(anomalies, [0.5]*len(anomalies), color='black', label='Injected Anomalies', zorder=5)
plt.title('Anomaly Detection Using Normal Distribution')
plt.xlabel('Transaction Amount ($)')
plt.ylabel('Frequency')
plt.legend()
plt.tight_layout()
plt.show()# Output detected anomalies
detected_anomalies

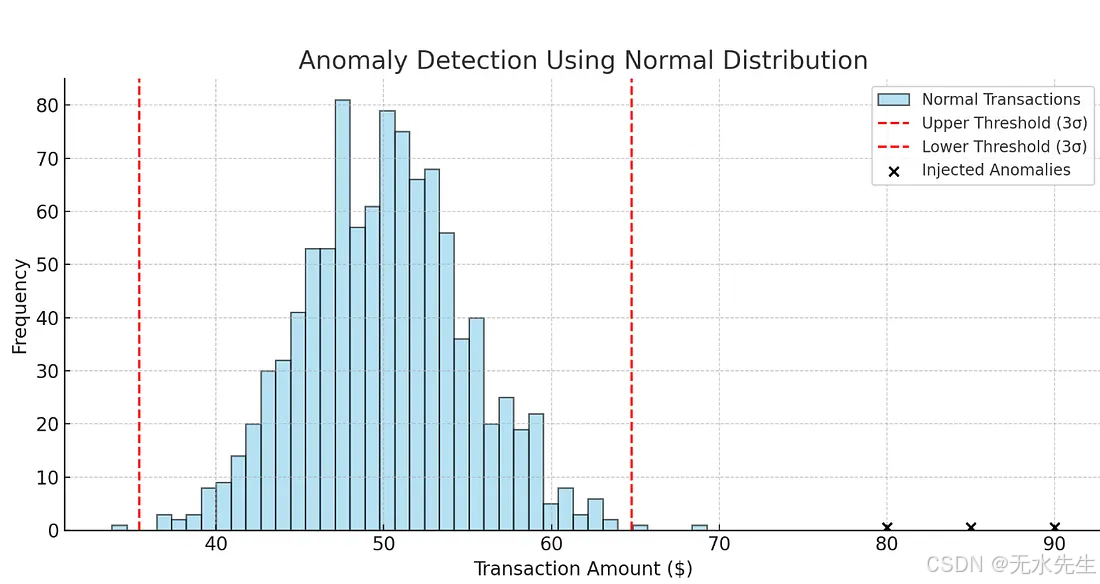
output detected_anomalies: array([69.26365745, 33.7936633 , 65.39440404, 80.        , 85.        ,       90.        ])

四、二项分布：反复抛同一枚硬币

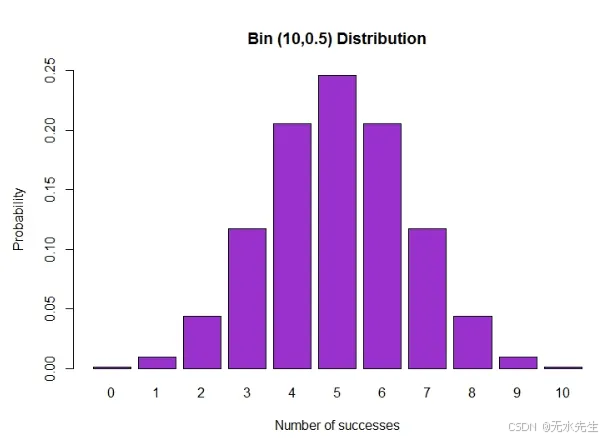
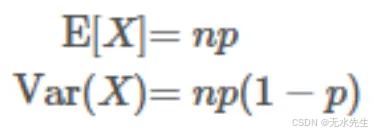
想象一下你正在抛硬币——不是一次，而是10次。你押注正面。有时你会得到5个正面，有时是7个，有时是3个。但如果你抛100次呢？或者1000次？得到恰好60个正面的可能性有多大？
这就是二项分布的世界——在这里，你计算在固定次数的试验中成功（如正面）的数量。
二项分布的使用时机
• 固定的试验次数n
• 只有两种可能的结果：成功（1）或失败（0）
• 每次试验成功的概率p是恒定的
• 试验是独立的
如果你对所有四个问题都回答“是”，你就进入了二项分布领域。
二项分布的视觉形状
• X轴：成功次数（从0到n）
• Y轴：观察到该数量成功事件的概率
• 形状取决于n和p：
• 当p=0.5时对称
• 当p远离0.5时偏斜
二项分布的参数
• n：试验次数
• p：每次试验成功的概率
• x：成功次数（离散结果）
为什么二项分布重要

概率质量函数（PMF）

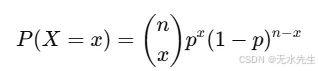
（n x) 表示从 n 次试验中选择 x 次成功的不同方法的数量。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
# Step 1: Define parameters
n = 20          # number of trials
p = 0.5         # probability of success
x = np.arange(0, n + 1)  # possible outcomes: 0 to n
# Step 2: Calculate the PMF
pmf = binom.pmf(x, n, p)
# Step 3: Plot the PMF
plt.figure(figsize=(10, 5))
plt.bar(x, pmf, color='teal', alpha=0.7)
plt.title(f'Binomial Distribution: n = {n}, p = {p}', fontsize=14)
plt.xlabel('Number of Successes', fontsize=12)
plt.ylabel('Probability Mass', fontsize=12)
plt.grid(axis='y')
plt.tight_layout()
plt.show()

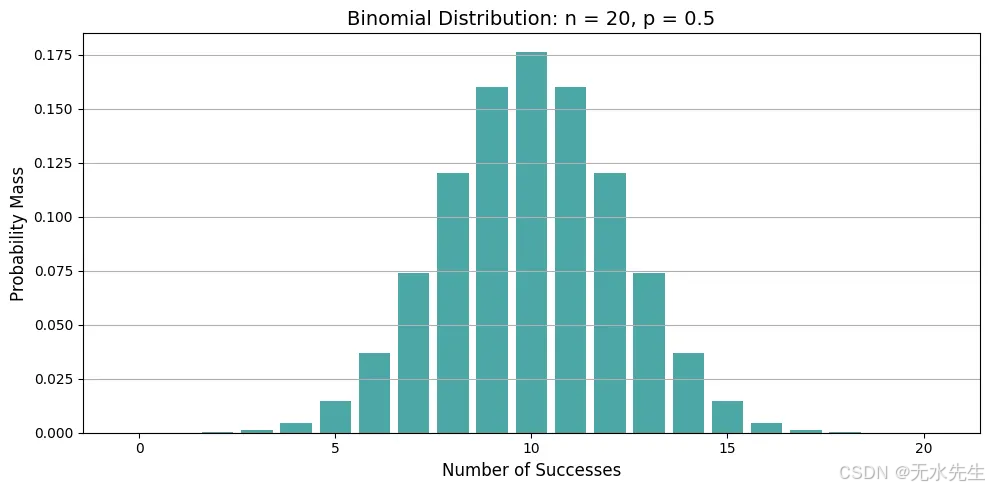
情节告诉我们什么？
• 极值接近n×p。这里，20×0.5=10，最可能的正面次数是10。
• 当p=0.5时，分布是对称的；当p<0.5时，向左偏斜；当p>0.5时，向右偏斜。
二项分布的机器学习应用
二项分布在统计建模和人工智能中有着深远的影响：

1. 分类可能性建模
   在二元分类（例如垃圾邮件与非垃圾邮件）中，预测类别为0或1。二项分布将其建模为：
   
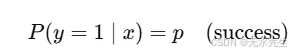
   它是逻辑回归的基础，在成本函数中使用伯努利似然（n=1的二项式情况）。
   模型评估：准确性和成功率至关重要。在评估模型时：
   • 准确性可以建模为二项分布
   • 假设您的模型在100次预测中正确预测了90次 → 您可以使用二项检验来建模和测试这一点

from scipy.stats import binom_test
binom_test(x=90, n=100, p=0.5, alternative='greater')  
# is 90/100 significantly better than chance?

3 A/B测试和假设检验
假设你在测试两个版本的网站：
• 版本A：1000访客→120次点击
• 版本B：1000访客→150次点击
使用二项分布来检验改进是否具有统计显著性。

零假设（H0）：两个版本的点击率（CTR）相同，p = 0.12，基于版本A。备择假设（H1）：版本B的点击率高于版本A。我们使用二项分布来建模版本B上的点击数：n=1000（试验次数=访客数），p=0.12（在H0下的预期成功率），观察到x=150次点击。现在我们进行测试：如果实际点击率为12%，获得150次或更多点击的概率是多少？

from scipy.stats import binomtest # Changed from binom_test# Parameters
n_B = 1000         # Number of visitors to version B
x_B = 150          # Number of clicks on version B
p_null = 0.12      # Baseline CTR from version A# Perform one-sided binomial test using binomtest
# The binomtest function returns an object with a pvalue attribute
result = binomtest(k=x_B, n=n_B, p=p_null, alternative='greater') # Changed parameter name from x to k
p_value = result.pvalue # Access the p-value from the result object# Output result
print(f"P-value: {p_value:.4f}")
if p_value < 0.05:print("Result: Statistically significant — Version B likely performs better.")
else:print("Result: Not statistically significant — the difference may be due to chance.")

P-value: 0.0026
Result: Statistically significant — Version B likely performs better.

p值为0.0062，小于0.05。因此，我们拒绝原假设，并得出结论：版本B的转化率可能高于版本A。二项式检验直接回答了：如果没有任何变化，仅凭偶然性获得150次或更多点击的可能性有多大？答案是：不太可能。
4. 在集成方法中建模罕见事件（如随机森林），如果每棵树都有一个小错误的概率，你可以使用二项式模型来估计整个森林做出错误预测的概率。
想象一下，你正在使用一个随机森林分类器来预测客户是否会违约贷款。
关于随机森林：
• 它们结合了许多决策树（例如，100棵树）。
• 每棵树进行投票：是（违约）或否（不违约）。
• 最终预测基于多数投票。
现在，假设：
• 每个单独的树在未见数据上的准确率为95％（错误率=5％）。
• 树是独立且随机训练的（由于引导+特征随机性）。
那么，超过一半的树（即100棵树中的51棵）在精确预测上出错的概率是多少？
这意味着整个森林给出错误的答案，即使单个树是准确的。
让我们使用二项分布
• 试验次数（树的数量）：n=100
• 每棵树失败的概率：p=0.05
• 随机变量X：投票错误的树的数量
• 我们

直觉：
• 每棵树就像抛一枚有5%概率投错票的加权硬币。
• 整个森林只有在罕见事件发生时才会失败：在100棵树中有51棵或更多的树投错了票。

from scipy.stats import binom# Parameters
n = 100      # Number of trees
p = 0.05     # Probability that a single tree makes a mistake# Probability that 51 or more trees make a mistake
prob_majority_error = binom.sf(50, n, p)  # sf = 1 - cdfprint(f"Probability that the forest gives the wrong answer: {prob_majority_error:.10f}")

Probability that the forest gives the wrong answer: 0.0000000000

解释
• 大多数树木同时失败的概率几乎是零。
• 即使每棵树稍微弱一些，整体仍然非常稳健。
• 这就是为什么集成方法，如随机森林，非常强大。它们通过投票减少方差和错误，二项分布提供了数学证明。
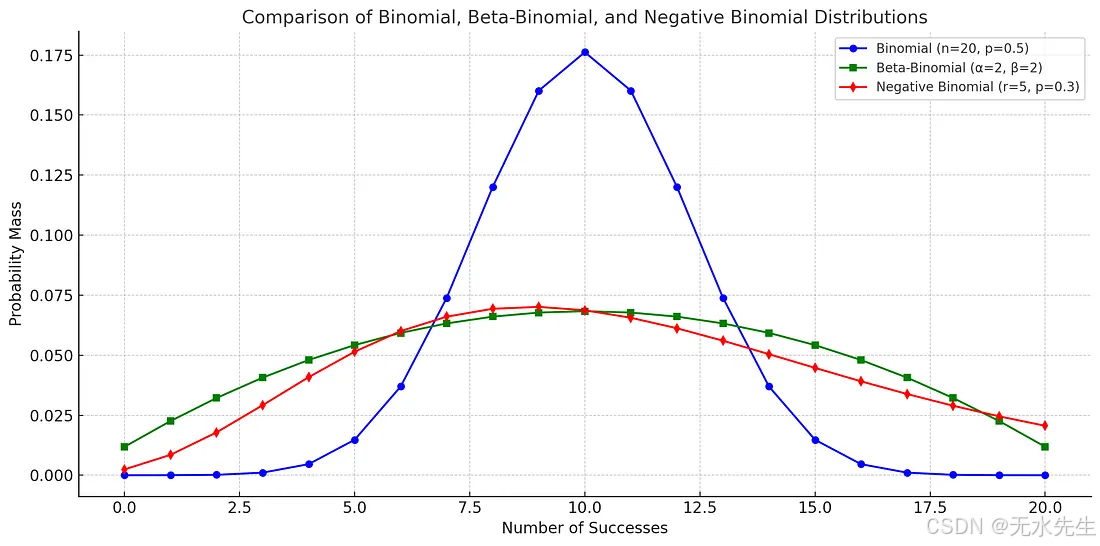
二项分布的变体
按Enter键或点击以查看完整大小的图片

三个二项分布的比较，都显示了观察到一定数量成功事件的概率。

# Recalculate all PMFs since the environment was reset# PMFs for each distribution (corrected)
binom_pmf = binom.pmf(x, n=n, p=p)
nbinom_pmf = nbinom.pmf(x, n=r, p=p_nb)
betabinom_pmf = betabinom.pmf(x, n=n, a=alpha, b=beta)# Plotting
plt.figure(figsize=(12, 6))plt.plot(x, binom_pmf, 'o-', label='Binomial (n=20, p=0.5)', color='blue')
plt.plot(x, betabinom_pmf, 's-', label='Beta-Binomial (α=2, β=2)', color='green')
plt.plot(x, nbinom_pmf[:n+1], 'd-', label='Negative Binomial (r=5, p=0.3)', color='red')plt.title('Comparison of Binomial, Beta-Binomial, and Negative Binomial Distributions', fontsize=14)
plt.xlabel('Number of Successes', fontsize=12)
plt.ylabel('Probability Mass', fontsize=12)
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()

五、泊松分布：当事件随机出现时

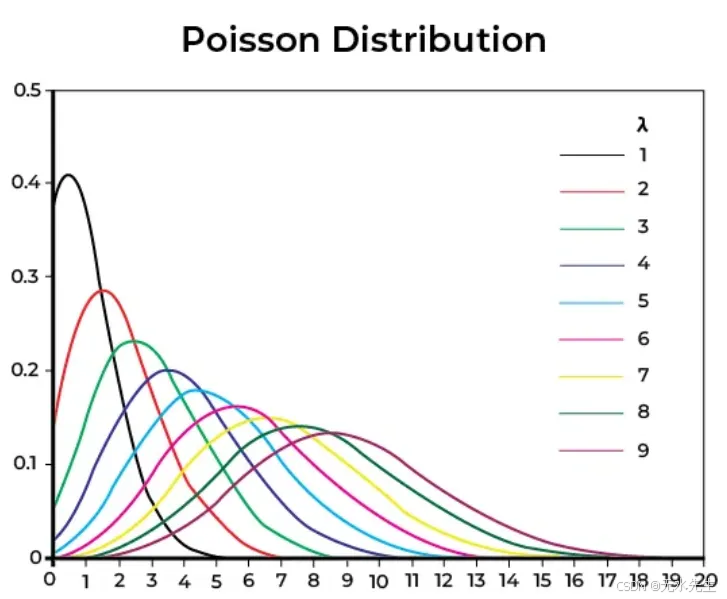
想象你在一家咖啡店工作。平均来说，每10分钟有3位顾客到来。有时是2位，有时是4位，偶尔可能是0位甚至6位，但平均而言，大约是3位。你不知道他们确切的到达时间，但你关心的是他们的数量。
这就是泊松分布——它用于模拟在固定时间段内发生的事件数量，假设这些事件独立发生且以恒定的平均速率发生。
泊松分布的视觉形状
• X轴：事件数量（例如，客户到达次数、点击次数、电话次数）
• Y轴：该数量事件的概率
形状是：
• 当λ较小时，右偏
• 随着λ增加，更对称
• 总是非负且离散的
泊松分布的参数
• λ：区间内的平均事件数（均值=方差）
概率质量函数（PMF）

Python代码：模拟泊松过程

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
# Step 1: Set the expected number of events
lambda_ = 3  # average number of events per interval
# Step 2: Define the possible range of event counts
x = np.arange(0, 15)
# Step 3: Calculate Poisson probabilities
pmf = poisson.pmf(x, mu=lambda_)
# Step 4: Plot the distribution
plt.figure(figsize=(10, 5))
plt.bar(x, pmf, color='orchid', alpha=0.7)
plt.title(f'Poisson Distribution (λ = {lambda_})', fontsize=14)
plt.xlabel('Number of Events (k)', fontsize=12)
plt.ylabel('Probability P(X = k)', fontsize=12)
plt.grid(axis='y')
plt.tight_layout()
plt.show()

平均来说，每10分钟有3位顾客到来。下一次10分钟内正好有5位顾客到来的概率是多少？

poisson.pmf(5, mu=3)

Output:

≈ 0.1008
因此，在那个时间窗口内有5名客户到达的概率是10%。泊松分布在机器学习中的应用泊松分布是许多机器学习和数据应用中的隐藏引擎：
1 在广义线性模型（GLM）中，当目标变量是计数数据时，使用泊松回归：
• 每个广告的点击次数
• 支持中心接收到的电话数量
• 产品线中的缺陷数量

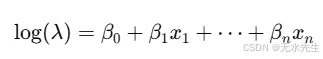
在statsmodels、sklearn（通过Tweedie）和PyTorch GLMs中使用。
示例：你管理一个客户服务中心，你想根据两个特征预测每小时的来电数量。

• 应用程序上的活跃用户数量（active_users）
• 是否在营业时间内（business_hours = 1 表示是，0 表示否）
  你怀疑随着更多用户活跃以及在营业时间内，支持电话的数量会增加。由于目标是计数数据（每小时的电话数量），因此使用泊松回归模型。

import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf# Step 1: Create a sample dataset
data = pd.DataFrame({'active_users': [150, 80, 230, 100, 300, 60, 200, 110, 180, 90],'business_hours': [1, 0, 1, 0, 1, 0, 1, 0, 1, 0],'calls_per_hour': [5, 1, 8, 2, 12, 1, 9, 2, 7, 1]
})# Step 2: Fit a Poisson regression modelmodel = smf.glm(formula='calls_per_hour ~ active_users + business_hours',data=data, family=sm.families.Poisson()).fit()# Step 3: Print the summary
print(model.summary())

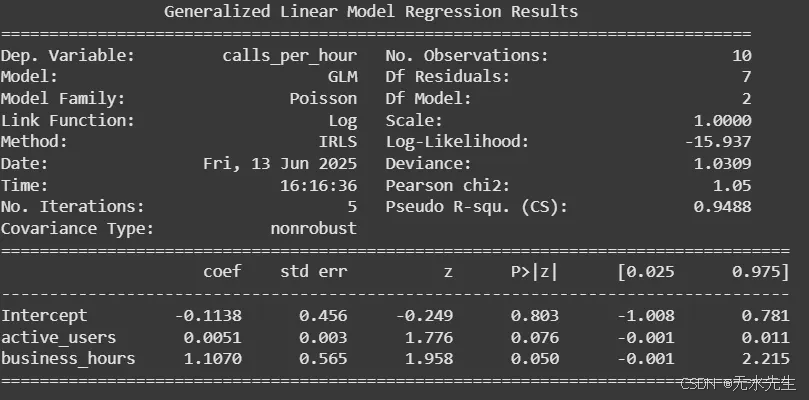
import numpy as np# Get coefficients
intercept = model.params['Intercept']
coef_users = model.params['active_users']
coef_hours = model.params['business_hours']# Compute predicted mean (λ)
log_lambda = intercept + coef_users * 200 + coef_hours * 1
lambda_ = np.exp(log_lambda)print(f"Expected calls per hour: {lambda_:.2f}")
Expected calls per hour: 7.45

2 在自然语言处理中，文本中的词频（例如，在短文档中）通常遵循类似泊松分布的模式：
• 文档中“the”或“data”的出现次数
• 推文的长度
• 每篇帖子中的标签出现次数
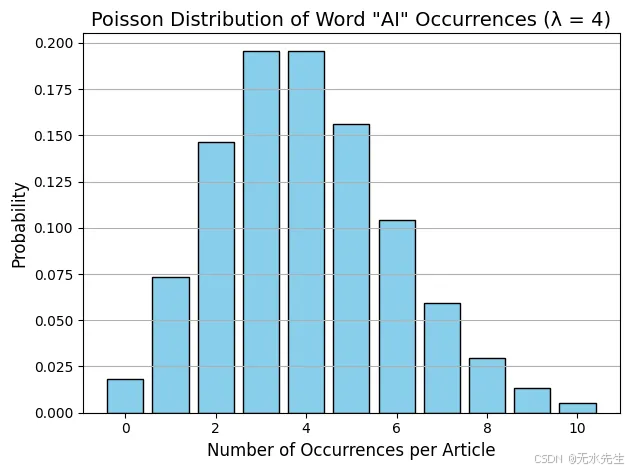
示例：你正在分析一组简短的新闻文章。你想建模特定关键词在文档中出现的频率，例如单词“AI”。

根据你的数据，你观察到平均每个文章中“AI”出现4次。现在，你想计算：“AI”在给定的文章中恰好出现6次的概率是多少？这时泊松分布正好适用。

from scipy.stats import poisson# Average number of times "AI" appears in an article
lambda_ = 4  # Probability that "AI" appears exactly 6 times
k = 6
prob_6_occurrences = poisson.pmf(k, mu=lambda_)print(f"Probability that 'AI' appears exactly 6 times: {prob_6_occurrences:.4f}")

AI’出现恰好6次的概率：0.1042，因此，在平均出现4次的情况下，文章中“AI”一词恰好出现6次的概率约为10.42%。

import numpy as np
import matplotlib.pyplot as pltx = np.arange(0, 11)
pmf = poisson.pmf(x, mu=4)plt.bar(x, pmf, color='skyblue', edgecolor='black')
plt.title('Poisson Distribution of Word "AI" Occurrences (λ = 4)', fontsize=14)
plt.xlabel('Number of Occurrences per Article', fontsize=12)
plt.ylabel('Probability', fontsize=12)
plt.grid(axis='y')
plt.tight_layout()
plt.show()

3 流量分析与异常检测
· 模型化服务器每分钟的请求数量。
· 当实际请求数远超预期时检测异常（例如，DDoS攻击）。
如果λ=100请求/分钟，然后突然有300个到达？
这是泊松分布中的低概率尾部事件，需要通知您的运营团队。

4 时间序列模拟用于事件预测。泊松分布常作为模拟的起点，
例如：

• 客流量

• 点击事件

• 客服中心通话量

特别是在事件独立且以固定平均速率发生的情况下。

示例：你管理一家零售店，想要模拟一天（10小时）内每小时到达的顾客数量。
根据历史数据，你知道：
• 平均每小时有10位顾客到达。
• 到达是随机的，但速率一致（适合使用泊松分布）。
• 每个小时都是独立的。

import numpy as np
import matplotlib.pyplot as plt# Step 1: Define simulation parameters
hours_open = 10               # Store is open for 10 hours
lambda_per_hour = 10          # Average of 10 customers per hour# Step 2: Simulate customer arrivals per hour
np.random.seed(42)  # for reproducibility
customer_arrivals = np.random.poisson(lam=lambda_per_hour, size=hours_open)# Step 3: Plot the time-series
hours = np.arange(1, hours_open + 1)plt.figure(figsize=(10, 5))
plt.plot(hours, customer_arrivals, marker='o', linestyle='-', color='steelblue')
plt.title('Simulated Hourly Customer Arrivals (Poisson Process)', fontsize=14)
plt.xlabel('Hour of the Day', fontsize=12)
plt.ylabel('Number of Customers', fontsize=12)
plt.grid(True)
plt.xticks(hours)
plt.tight_layout()
plt.show()# Optional: Show raw numbers
for hr, cust in zip(hours, customer_arrivals):print(f"Hour {hr}: {cust} customers")

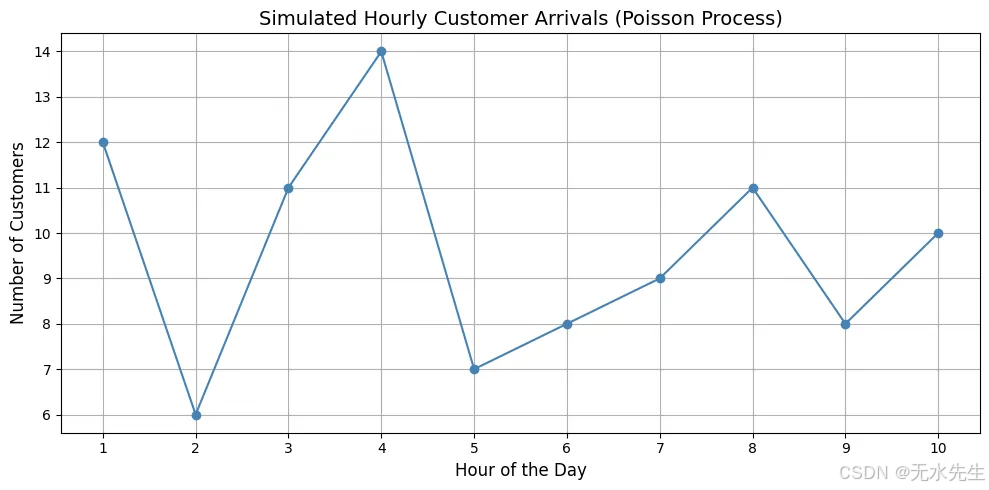
泊松过程在均值（10）周围提供自然波动。有时它会激增（13），有时它会下降（8），但始终保持中心位置。非常适合用于预测和规划（例如，确定需要安排的员工数量）。

5 在贝叶斯建模中：

• 泊松似然和伽马先验形成共轭对。

• 用于实时更新关于速率（λ）的信念。

示例：

你运营一个新闻网站，想估计每篇文章平均用户评论数，用λ表示。

你观察到：

• 每篇文章的评论数量遵循泊松分布（离散计数数据）。
• 但是你不知道λ的真实值，所以你在其上放置一个伽马先验来表达你的不确定性。你从一个信念（先验）开始，观察数据，然后更新你的信念——这就是贝叶斯推断的实际应用。
• 
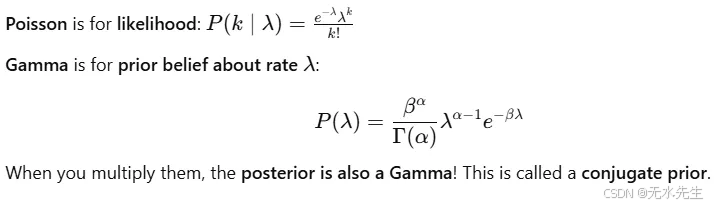
  你假设：
• λ∼Gamma(α=2,β=1)：先验信念——你认为大多数文章大约有2条评论。你观察到4篇文章，评论数分别为[3, 2, 4, 1]。
• 你对每篇文章平均评论数λ的更新信念（后验）是什么？

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma# Prior parameters
alpha_prior = 2
beta_prior = 1# Observed data (comments per article)
data = np.array([3, 2, 4, 1])
total_comments = np.sum(data)
n_observations = len(data)# Posterior parameters
alpha_post = alpha_prior + total_comments
beta_post = beta_prior + n_observations# Define range of lambda values
lambdas = np.linspace(0, 10, 500)
posterior_pdf = gamma.pdf(lambdas, a=alpha_post, scale=1 / beta_post)# Plotting
plt.figure(figsize=(10, 5))
plt.plot(lambdas, posterior_pdf, label=f'Posterior: Gamma({alpha_post}, {beta_post})', color='darkgreen')
plt.title('Posterior Distribution of λ (Avg. Comments per Article)', fontsize=14)
plt.xlabel('λ (Average Comments per Article)', fontsize=12)
plt.ylabel('Probability Density', fontsize=12)
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()

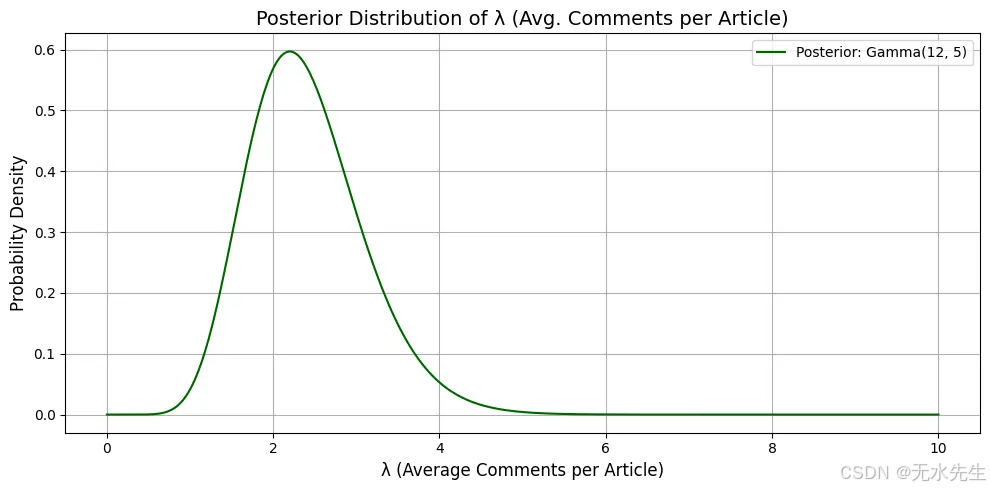
解释：
• 后验峰值（众数）大约在12−15=2.2，反映了你在看到数据后更新的信念，即每篇文章平均评论数约为2.2。
• Gamma分布反映了你的信心；它很窄，意味着在看到数据后，你的信念变得更加明确。

六、结论

总之，理解概率分布就像学习不确定性背后的秘密语言。从均匀分布的平衡公平到正态曲线的钟形美丽，以及二项分布、泊松分布等现实世界的节奏，这些工具使我们能够建模、预测并做出更明智的决策。无论你是构建机器学习模型还是仅仅试图理解数据中的模式，掌握分布是迈向解锁更深层次见解的重要一步。