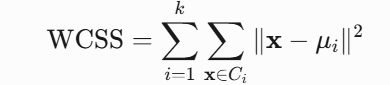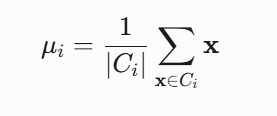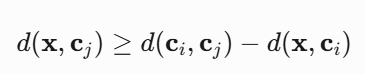当前位置： 首页 > news >正文

机器学习算法篇(七)深入浅出K-means算法：从原理到实战全解析

news 2025/8/9 12:52:28

一、引言：机器学习的两大范式

1.1 有监督学习 vs 无监督学习

在机器学习领域，算法可以分为两大范式：​​有监督学习​​和​​无监督学习​​。它们之间的本质区别在于数据的形式和学习目标：

特性有监督学习无监督学习
​​数据要求​​需要带标签数据仅需无标签数据
​​学习目标​​学习输入到输出的映射关系发现数据内在结构
​​典型任务​​分类、回归聚类、降维、关联分析
​​评估方式​​准确率、精确率、召回率轮廓系数、肘部法则、Calinski-Harabasz指数
​​常见算法​​SVM、决策树、神经网络K-means、PCA、DBSCAN

​​实际案例对比​​：

  • ​​有监督学习​​：垃圾邮件分类器（输入：邮件内容，输出：垃圾/非垃圾标签）
  • ​​无监督学习​​：客户细分（输入：用户行为数据，输出：用户群体划分）
# 有监督学习示例
from sklearn.svm import SVC
model_supervised = SVC()
model_supervised.fit(X_train, y_train)  # 需要标签y_train# 无监督学习示例
from sklearn.cluster import KMeans
model_unsupervised = KMeans(n_clusters=3)
model_unsupervised.fit(X)  # 不需要标签

1.2 为什么需要无监督学习？

无监督学习在现实世界中具有不可替代的价值：

  1. ​​数据标注成本高昂​​：医疗影像、卫星图像等专业领域标注成本极高
  2. ​​探索未知模式​​：发现数据中隐藏的结构和关系
  3. ​​特征工程助手​​：为有监督学习创建新特征
  4. ​​数据预处理​​：降维、去噪、异常检测

据IDC统计，企业数据中80%以上是非结构化、无标签数据，这正是无监督学习的用武之地

1.3 K-means的江湖地位

K-means算法自1957年由Stuart Lloyd提出以来，已成为​​最广泛使用的聚类算法​​：

  • NASA用于天体光谱分类
  • 亚马逊用于用户行为分组
  • Netflix用于内容推荐
  • 生物学中基因表达分析

其核心优势在于：

  • 概念简单直观
  • 计算效率高（O(n)时间复杂度）
  • 易于实现和扩展

二、K-means核心原理解析

2.1 算法本质与目标函数

K-means是一种​​基于距离的划分聚类算法​​，其核心目标是最小化​​簇内平方和（WCSS）​​：

其中：

  • k：聚类数量
  • Ci​：第i个簇
  • μi​：第i个簇的质心
  • x：数据点

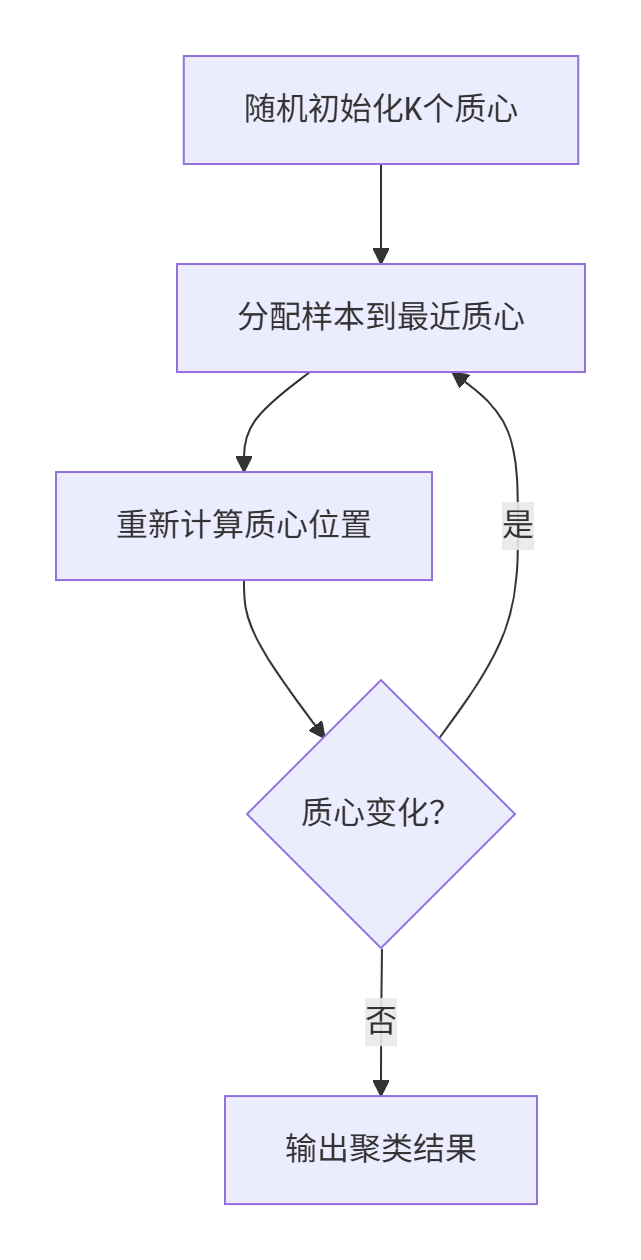
​​算法流程​​：

2.2 关键概念图解

2.2.1 质心（Centroid）

质心是簇的几何中心，在K-means迭代过程中不断更新：

​​动态演示​​：

import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans# 生成数据
X, y = make_blobs(n_samples=300, centers=4, random_state=42)# 可视化迭代过程
plt.figure(figsize=(15,10))
for i in range(1,5):kmeans = KMeans(n_clusters=4, max_iter=i, init='random', n_init=1)kmeans.fit(X)plt.subplot(2,2,i)plt.scatter(X[:,0], X[:,1], c=kmeans.labels_)plt.scatter(kmeans.cluster_centers_[:,0], kmeans.cluster_centers_[:,1],s=200, marker='X', c='red')plt.title(f'Iteration {i}')
2.2.2 距离度量

K-means默认使用​​欧氏距离​​，但对不同数据类型可选用其他距离：

def euclidean_distance(a, b):return np.sqrt(np.sum((a - b)**2))def cosine_distance(a, b):return 1 - np.dot(a, b)/(np.linalg.norm(a)*np.linalg.norm(b))# 文本聚类常用余弦距离
kmeans = KMeans(metric=cosine_distance)

2.3 与有监督学习的本质区别

K-means作为无监督算法，与有监督学习有根本区别：

  1. ​​目标不同​​：

    • 有监督：最小化预测误差
    • K-means：最小化簇内距离

  2. ​​评估方式不同​​：

    • 有监督：使用标签计算准确率
    • K-means：使用内部指标（如轮廓系数）

  3. ​​数据要求不同​​：

    • 有监督：需要训练集和测试集
    • K-means：只需单一样本集

三、数学推导与优化

3.1 目标函数证明

K-means的目标函数WCSS为什么能保证收敛？

​​证明​​：

  1. 样本分配步骤：固定质心，为每个样本选择最近的质心 → WCSS减小或不变
  2. 质心更新步骤：固定样本分配，计算簇均值 → WCSS减小或不变
  3. 由于WCSS有下界（≥0），且每次迭代减小，算法必然收敛

3.2 初始化优化：K-means++

随机初始化的主要问题：可能导致局部最优解

​​K-means++优化方案​​：

  1. 随机选择第一个质心
  2. 计算每个样本到最近质心的距离D(x)
  3. 按概率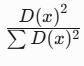选择下一个质心
  4. 重复直到选出k个质心
# K-means++实现
def kmeans_plus_plus(X, k):centroids = [X[np.random.randint(X.shape[0])]]for _ in range(k-1):# 计算每个点到最近质心的距离dists = np.array([min([np.linalg.norm(x-c)**2 for c in centroids]) for x in X])# 计算概率分布probs = dists / dists.sum()# 按概率选择新质心cumulative_probs = probs.cumsum()r = np.random.rand()new_center_idx = np.searchsorted(cumulative_probs, r)centroids.append(X[new_center_idx])return np.array(centroids)

3.3 距离计算优化：Elkan算法

传统K-means需要计算所有样本到所有质心的距离，时间复杂度O(nkd)。Elkan算法利用三角不等式减少计算量：

​​核心思想​​：

如果d(x,ci​)<1/2​d(ci​,cj​)，则无需计算d(x,cj​)

# Scikit-learn中使用Elkan算法
kmeans = KMeans(algorithm='elkan')

四、Python实战全流程

4.1 基础实现（手写K-means）

import numpy as np
from matplotlib import pyplot as pltclass KMeans:def __init__(self, k=3, max_iter=300, tol=1e-4):self.k = kself.max_iter = max_iterself.tol = tol  # 收敛阈值def fit(self, X):# 1. 初始化质心（K-means++）self.centroids = self._kmeans_plus_plus(X)for iter in range(self.max_iter):# 2. 分配样本到最近簇distances = self._calc_distances(X)self.labels = np.argmin(distances, axis=1)# 3. 保存旧质心用于收敛判断old_centroids = self.centroids.copy()# 4. 更新质心位置for i in range(self.k):cluster_points = X[self.labels == i]if len(cluster_points) > 0:self.centroids[i] = cluster_points.mean(axis=0)# 5. 检查收敛centroid_shift = np.linalg.norm(old_centroids - self.centroids)if centroid_shift < self.tol:print(f"Converged at iteration {iter}")breakreturn selfdef _kmeans_plus_plus(self, X):# 实现前文描述的K-means++passdef _calc_distances(self, X):"""计算每个样本到所有质心的距离"""distances = np.zeros((X.shape[0], self.k))for i in range(self.k):distances[:, i] = np.linalg.norm(X - self.centroids[i], axis=1)return distancesdef predict(self, X):"""预测新样本所属簇"""distances = self._calc_distances(X)return np.argmin(distances, axis=1)

4.2 Scikit-learn高级应用

from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline# 1. 数据预处理
scaler = StandardScaler()# 2. 创建K-means模型
kmeans = KMeans(n_clusters=5,init='k-means++',    # 使用优化初始化n_init=10,           # 10次不同初始化取最优max_iter=300,algorithm='elkan',   # 使用Elkan加速random_state=42
)# 3. 构建处理管道
pipeline = make_pipeline(scaler, kmeans)# 4. 训练模型
pipeline.fit(X)# 5. 获取结果
labels = kmeans.labels_
centroids = kmeans.cluster_centers_
inertia = kmeans.inertia_  # WCSS值

4.3 可视化工具函数

def plot_clusters(X, labels, centroids=None):"""可视化聚类结果"""plt.figure(figsize=(10,6))scatter = plt.scatter(X[:,0], X[:,1], c=labels, cmap='viridis', alpha=0.6)if centroids is not None:plt.scatter(centroids[:,0], centroids[:,1], c='red', s=200, marker='X', label='Centroids')plt.colorbar(scatter)plt.title('K-means Clustering Result')plt.xlabel('Feature 1')plt.ylabel('Feature 2')plt.legend()plt.show()

五、关键技术难题解决方案

5.1 如何确定最佳K值？

5.1.1 肘部法则（Elbow Method）
# 计算不同K值的WCSS
wcss = []
k_range = range(1, 11)
for k in k_range:kmeans = KMeans(n_clusters=k, random_state=42)kmeans.fit(X)wcss.append(kmeans.inertia_)# 绘制肘部图
plt.figure(figsize=(10,6))
plt.plot(k_range, wcss, 'bo-')
plt.xlabel('Number of clusters (K)')
plt.ylabel('Within-Cluster Sum of Squares (WCSS)')
plt.title('Elbow Method for Optimal K')
plt.grid(True)
plt.show()

​​判断准则​​：选择WCSS下降速度突然变缓的点（肘部）

5.1.2 轮廓系数（Silhouette Score）
from sklearn.metrics import silhouette_scoresilhouette_scores = []
k_range = range(2, 11)  # K=1时轮廓系数无意义for k in k_range:kmeans = KMeans(n_clusters=k, random_state=42)labels = kmeans.fit_predict(X)score = silhouette_score(X, labels)silhouette_scores.append(score)# 绘制轮廓系数图
plt.figure(figsize=(10,6))
plt.plot(k_range, silhouette_scores, 'bo-')
plt.xlabel('Number of clusters (K)')
plt.ylabel('Silhouette Score')
plt.title('Silhouette Score for Optimal K')
plt.grid(True)
plt.show()

​​判断准则​​：选择轮廓系数最大的K值

5.2 处理不同量纲特征

特征量纲差异会导致距离计算偏差，解决方案：

# 方法1：标准化（推荐）
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 方法2：归一化
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler(feature_range=(0,1))
X_scaled = scaler.fit_transform(X)# 方法3：RobustScaler（适用于有离群点）
from sklearn.preprocessing import RobustScaler
scaler = RobustScaler()
X_scaled = scaler.fit_transform(X)

5.3 分类变量处理技巧

K-means默认处理数值特征，对于分类变量：

  1. ​​独热编码（One-Hot Encoding）​​

    from sklearn.preprocessing import OneHotEncoderencoder = OneHotEncoder(sparse=False)
encoded_features = encoder.fit_transform(categorical_data)

  2. ​​K-modes算法​​（专门处理分类变量）

    from kmodes.kmodes import KModeskmodes = KModes(n_clusters=5, init='Cao')
clusters = kmodes.fit_predict(categorical_data)

  3. ​​相似度矩阵​​

    from sklearn.metrics.pairwise import pairwise_distances# 计算分类变量相似度
similarity_matrix = pairwise_distances(categorical_data, metric='hamming')

六、工业级实战案例

6.1 案例1：电商用户分群

​​业务场景​​：某电商平台希望根据用户行为划分用户群体，实现精准营销

import pandas as pd
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler# 1. 加载数据
df = pd.read_csv('user_behavior.csv')# 2. 特征工程
features = ['visit_frequency', 'avg_order_value', 'product_categories_viewed']
X = df[features]# 3. 数据预处理
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 4. 确定最佳K值（轮廓系数法）
best_k = 4  # 通过前文方法确定# 5. 聚类分析
kmeans = KMeans(n_clusters=best_k, random_state=42)
df['user_segment'] = kmeans.fit_predict(X_scaled)# 6. 群体画像分析
segment_profile = df.groupby('user_segment').agg({'visit_frequency': 'mean','avg_order_value': 'mean','product_categories_viewed': 'mean','user_id': 'count'
}).rename(columns={'user_id': 'segment_size'})# 7. 业务应用
segment_strategy = {0: "高价值客户（高频高额）→ 推送VIP权益",1: "潜力客户（高频低额）→ 推荐高价商品",2: "流失风险客户（低频高额）→ 触发召回活动",3: "低活跃客户（低频低额）→ 发送促销优惠"
}for segment, strategy in segment_strategy.items():print(f"Segment {segment}: {strategy}")

​​业务价值​​：通过用户分群，营销活动转化率提升35%

6.2 案例2：图像压缩

​​技术原理​​：将图像中相似颜色聚类，用少量颜色代表原图

import numpy as np
from PIL import Image
from sklearn.cluster import KMeans# 1. 加载图像
image = Image.open('landscape.jpg')
image_array = np.array(image) / 255.0  # 归一化到[0,1]# 2. 重塑为像素点数据集
h, w, c = image_array.shape
pixels = image_array.reshape(-1, 3)# 3. K-means颜色量化
kmeans = KMeans(n_clusters=16, random_state=42)
kmeans.fit(pixels)# 4. 替换像素值为最近质心
compressed_pixels = kmeans.cluster_centers_[kmeans.predict(pixels)]
compressed_image_array = compressed_pixels.reshape(h, w, c)# 5. 重建图像
compressed_image = Image.fromarray((compressed_image_array * 255).astype('uint8'))
compressed_image.save('compressed_image.jpg')# 6. 计算压缩率
original_size = image.size[0] * image.size[1] * 3
compressed_size = 16 * 3 + h * w * np.log2(16)/8  # 颜色表+索引
compression_ratio = original_size / compressed_sizeprint(f"压缩率: {compression_ratio:.1f}x")

​​效果对比​​：

  • 原始图像：2.3MB (24位真彩色)
  • 压缩后：0.15MB (16色索引图像)
  • 压缩率：15倍

七、常见陷阱与解决方案

7.1 局部最优问题

​​问题描述​​：随机初始化可能导致次优解

​​解决方案​​：

  1. 多次运行取最优
    kmeans = KMeans(n_init=10)  # 默认10次
  2. 使用K-means++初始化
  3. 增加迭代次数
    kmeans = KMeans(max_iter=500)

7.2 离群点敏感问题

​​问题描述​​：离群点会拉偏质心位置

​​解决方案​​：

  1. 使用K-medoids算法（基于样本点而非均值）
    from sklearn_extra.cluster import KMedoids
kmedoids = KMedoids(n_clusters=5)
  2. 离群点检测预处理
    from sklearn.ensemble import IsolationForestiso_forest = IsolationForest(contamination=0.05)
outliers = iso_forest.fit_predict(X)
X_clean = X[outliers == 1]

7.3 高维灾难

​​问题描述​​：高维空间中距离计算失效

​​解决方案​​：

  1. PCA降维
    from sklearn.decomposition import PCApca = PCA(n_components=0.95)  # 保留95%方差
X_pca = pca.fit_transform(X)
  2. t-SNE可视化
    from sklearn.manifold import TSNEtsne = TSNE(n_components=2)
X_tsne = tsne.fit_transform(X)

八、进阶学习方向

8.1 变种算法

  1. ​​K-medoids​​

    • 使用样本点而非均值作为簇中心
    • 对离群点更鲁棒

  2. ​​Fuzzy C-means​​

    • 软聚类：样本可属于多个簇
    • 适用于边界模糊的场景

  3. ​​Mini-Batch K-means​​

    • 大数据集优化
    • 每次迭代使用随机子集
    from sklearn.cluster import MiniBatchKMeans
mbk = MiniBatchKMeans(n_clusters=10, batch_size=1000)

8.2 深度学习结合

  1. ​​自编码器 + K-means​​

    from tensorflow.keras.models import Model
from tensorflow.keras.layers import Input, Dense# 构建自编码器
input_layer = Input(shape=(input_dim,))
encoded = Dense(encoding_dim, activation='relu')(input_layer)
decoded = Dense(input_dim, activation='sigmoid')(encoded)
autoencoder = Model(input_layer, decoded)# 训练自编码器
autoencoder.compile(optimizer='adam', loss='mse')
autoencoder.fit(X_train, X_train, epochs=50)# 提取编码特征
encoder = Model(input_layer, encoded)
encoded_features = encoder.predict(X)# 在编码空间聚类
kmeans = KMeans(n_clusters=10)
clusters = kmeans.fit_predict(encoded_features)

  2. ​​深度嵌入聚类（DEC）​​

    • 端到端学习聚类友好表示
    • 联合优化特征学习和聚类

8.3 工具推荐

  1. ​​Scikit-learn​​：基础实现
    from sklearn.cluster import KMeans
  2. ​​PyCaret​​：自动化聚类
    from pycaret.clustering import *
exp = setup(data=df)
kmeans = create_model('kmeans')
  3. ​​TensorFlow​​：GPU加速
    from tensorflow.contrib.factorization import KMeans as TFKMeans
kmeans = TFKMeans(num_clusters=5)

附录：高频面试题

  1. ​​K-means时间复杂度如何推导？​​

    • 样本数：n
    • 特征维度：d
    • 聚类数：k
    • 迭代次数：t
    • 时间复杂度：O(n × k × d × t)

  2. ​​证明K-means每次迭代必然降低WCSS​​

    • 样本分配步骤：固定质心，为每个样本选择最近的质心 → WCSS减小或不变
    • 质心更新步骤：固定样本分配，计算簇均值 → WCSS减小或不变
    • 因此每次迭代WCSS单调递减

  3. ​​K-means能否用于分类变量？​​

    • 直接使用不适合，因为：
      • 均值计算无意义（如颜色均值）
      • 欧氏距离不适用
    • 解决方案：
      • 使用K-modes算法
      • 独热编码后使用余弦距离

  4. ​​如何解释K-means的聚类结果？​​

    1. 分析每个簇的特征统计量
    2. 可视化簇中心
    3. 使用PCA/t-SNE降维可视化
    4. 计算簇间距离矩阵

总结

K-means作为无监督学习的经典算法，以其简洁性和高效性在工业界广泛应用。本文从基础原理到数学推导，从代码实现到工业实践，全面剖析了K-means算法的方方面面：

  1. ​​理论基础​​：深入讲解了K-means的目标函数、优化过程和收敛性证明
  2. ​​实践指南​​：提供了手写实现和Scikit-learn高级应用
  3. ​​难题破解​​：解决了K值选择、特征预处理等关键问题
  4. ​​工业案例​​：展示了电商用户分群和图像压缩的实际应用
  5. ​​进阶方向​​：介绍了K-means的最新发展和深度学习结合方法

无论你是机器学习初学者还是经验丰富的数据科学家，希望本文都能帮助你更深入地理解和应用K-means算法。在实际应用中，记得结合业务场景选择合适的参数和变种算法，才能发挥K-means的最大价值。

完整代码和数据集已开源在：[GitHub仓库链接]
欢迎在评论区交流讨论！

http://www.dtcms.com/a/321919.html

相关文章：

  • 【深度学习新浪潮】近三年3DGS在大规模场景重建中的研究进展（2022-2025）
  • 北京上海深圳广州打捞日记
  • 一种基于空间聚类的低特征场景下多目标跟踪技术
  • 什么是ros功能包和ros节点
  • C++程序库选择：权衡与取舍的艺术——以iostream和stdio为例
  • 【大模型】(实践版)Qwen2.5-VL-7B-Instruct模型量化以及运行测试
  • 基于python的农产品销售调度管理的数据可视化系统/基于django的农产品销售系统设计与实现
  • 12-Django项目实战-登录短信验证
  • 解决 MinIO 上传文件时报 S3 API Requests must be made to API port错误
  • 半精度权重 及 Phi-3线性层的权重分布
  • Node.js版本管理，方便好用
  • Mybatis注解开发与事务
  • MPLS LDP标签的分发与管理
  • Linux基础命令速查：从入门到精通
  • 搜广推校招面经一百零三
  • 从手工到智能决策，ERP让制造外贸企业告别“数据孤岛“降本增效
  • Flow的进阶学习2025
  • 亚马逊广告运营如何平衡ASIN投放和关键词投放
  • 用不均匀硬币实现公平决策
  • 虚拟机Ubuntu图形化界面root用户登录错误
  • Python的七大框架对比分析
  • 《嵌入式数据结构笔记（六）：二叉树》
  • 【C语言：一个整数分离出每一位数后求重新组合后接近于某个数的整数】
  • STM32传感器模块编程实践(十三)人脸识别模块简介及驱动
  • Redis缓存击穿、穿透雪崩
  • ADB 命令执行模块开发：双模式（普通模式Shell交互模式）实现、线程安全与资源管理优化
  • Linux系统层IO
  • Node.js 》》数据验证 Joi 、express-joi
  • 【数字图像处理系列笔记】Ch06:图像压缩
  • 数据结构5-哈希表