最长公共子序列-动态规划
最长公共子序列
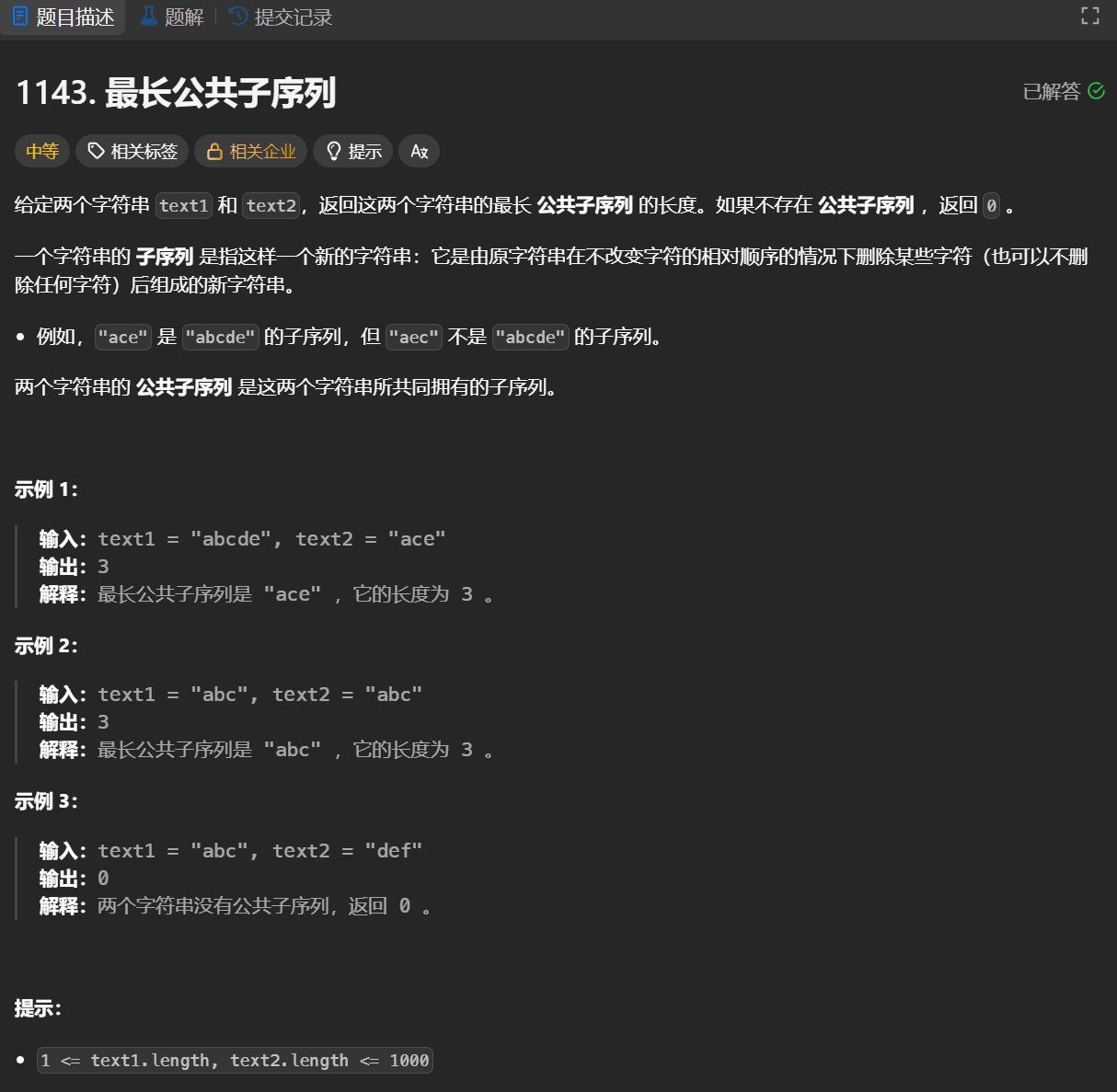
Solution
从递归到dp到空间优化。
#include<iostream>
#include<vector>
#include<string>
using namespace std;//我的递归思路
int f1(string s1, string s2, int i, int j) {//f1(i,j)表示s1从i到结尾与s2从j到结尾的最长公共子序列长度int n1 = s1.length();int n2 = s2.length();if (i >= n1 || j >= n2) return 0;int ans = 0;if (s1[i] == s2[j]) {ans = f1(s1, s2, i + 1, j + 1) + 1;}else {ans = max(f1(s1, s2, i, j + 1), f1(s1, s2, i + 1, j));}return ans;
}//带缓存表的递归
int f2(string s1, string s2, int i, int j, vector<vector<int>>& dp) {int n1 = s1.length();int n2 = s2.length();if (i >= n1 || j >= n2) return 0;if (dp[i][j] != -1) return dp[i][j];int ans = 0;if (s1[i] == s2[j]) {ans = f2(s1, s2, i + 1, j + 1, dp) + 1;}else {ans = max(f2(s1, s2, i, j + 1, dp), f2(s1, s2, i + 1, j, dp));}dp[i][j] = ans;return ans;
}//以长度为参数的递归(与我的想法反过来)
//f3(len1,len2)表示s1从开头len1长度的子串和s2从开头len2长度的子串的最长公共子序列的长度
int f3(string s1, string s2, int len1, int len2) {int n1 = s1.length();int n2 = s2.length();if (len1 == 0 || len2 == 0) return 0;int ans = 0;if (s1[len1 - 1] == s2[len2 - 1]) {ans = f3(s1, s2, len1 - 1, len2 - 1) + 1;}else {ans = max(f3(s1, s2, len1 - 1, len2), f3(s1, s2, len1, len2 - 1));}return ans;
}//严格位置依赖的动态规划
int f4(string s1, string s2) {int n1 = s1.length();int n2 = s2.length();vector<vector<int>>dp(n1 + 1, vector<int>(n2 + 1, 0));for (int i = n1 - 1; i >= 0; --i) {for (int j = n2 - 1; j >= 0; --j) {if (s1[i] == s2[j]) dp[i][j] = dp[i + 1][j + 1] + 1;else {dp[i][j] = max(dp[i + 1][j], dp[i][j + 1]);}}}return dp[0][0];
}
//严格位置依赖的动态规划+空间压缩
int f5(string s1, string s2) {int n1 = s1.length();int n2 = s2.length();string s3;if (n2 > n1) { s3 = s1; s1 = s2; s2 = s3; }n1 = s1.length();n2 = s2.length();vector<int>dp(n2 + 1, 0);for (int i = n1 - 1; i >= 0; --i) {int rightdown = 0, last;for (int j = n2 - 1; j >= 0; --j) {last = dp[j];if (s1[i] == s2[j]) dp[j] = rightdown + 1;else {dp[j] = max(dp[j], dp[j + 1]);}rightdown = last;}}return dp[0];
}
int longestCommonSubsequence1(string text1, string text2) {return f1(text1, text2, 0, 0);
}int longestCommonSubsequence2(string text1, string text2) {int n1 = text1.length();int n2 = text2.length();vector<vector<int>> dp(n1 + 1, vector<int>(n2 + 1, -1));return f2(text1, text2, 0, 0, dp);
}int longestCommonSubsequence3(string text1, string text2) {int n1 = text1.length();int n2 = text2.length();return f3(text1, text2, n1, n2);
}int longestCommonSubsequence4(string text1, string text2) {return f4(text1, text2);
}int longestCommonSubsequence(string text1, string text2) {return f5(text1, text2);
}
int main() {return 0;
}