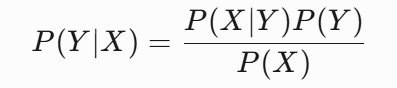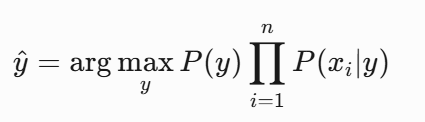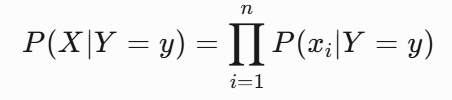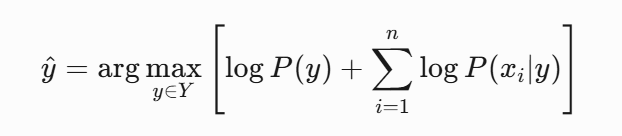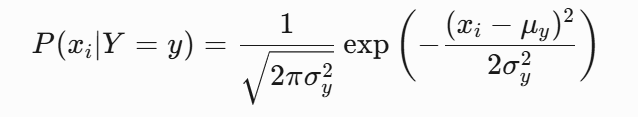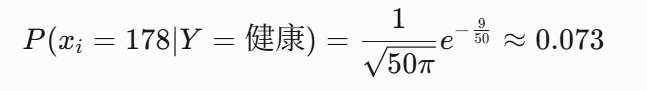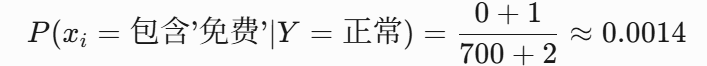机器学习算法篇（六）贝叶斯算法

引言

---

贝叶斯算法是机器学习中一类重要的概率分类方法，它以贝叶斯定理为基础，通过计算样本属于各个类别的概率来进行分类决策。其中，朴素贝叶斯（Naive Bayes）是最为经典和广泛应用的变种，因其简单高效的特点，在文本分类、垃圾邮件过滤、情感分析等领域有着卓越表现。本文将系统介绍贝叶斯算法的核心理论、实现流程、Python实践以及优缺点分析，帮助读者全面掌握这一重要算法。..

---

一、算法核心理论基础

1.1 贝叶斯定理

贝叶斯定理是概率论中的核心定理，描述了在已知某些条件下事件发生的概率如何更新。其数学表达式为：

其中：

• P(Y∣X) 是后验概率，表示在观察到特征X后，类别Y的概率
• P(X∣Y) 是似然概率，表示在类别Y下观察到特征X的概率
• P(Y) 是先验概率，表示类别Y的初始概率
• P(X) 是证据因子，通常作为归一化常数

在分类问题中，我们通常比较不同类别Y的后验概率P(Y∣X)，选择概率最大的类别作为预测结果。由于P(X)对所有类别相同，实际计算中可以忽略，只需比较分子部分：

1.2 朴素的条件独立性假设

"朴素"一词源于算法做了一个关键假设：所有特征在给定类别条件下相互独立。这意味着：

这一假设大大简化了计算复杂度，使得算法可以高效处理高维特征。虽然现实中特征间往往存在依赖关系，但大量实践表明，即使在这种简化假设下，朴素贝叶斯仍能取得令人满意的分类效果。

1.3 分类决策规则

朴素贝叶斯采用最大后验概率（MAP）决策规则：对于输入样本X，计算其属于每个类别的后验概率，并将概率最大的类别作为预测输出：

​

为了避免数值下溢（多个小概率相乘导致结果趋近于0），实际实现中常采用对数概率：

这里的argmax（yY）在所有可能的类别 y（属于集合 Y）中，找到使方括号内表达式 [logP(y)+∑logP(xi​∣y)]取得最大值的那个特定类别 y​

二、数据预处理之后的算法流程

2.1 训练阶段（参数估计）

2.1.1 计算先验概率

先验概率P(Y=y)表示各类别在训练数据中的初始分布，通过统计各类别样本数计算：

P(Y=y)=总样本数类别y的样本数​

​​示例​​：在一个包含1000封邮件的训练集中，垃圾邮件300封，正常邮件700封。则：

• P(Y=垃圾邮件)=1000300​=0.3
• P(Y=正常邮件)=1000700​=0.7

2.1.2 计算似然概率

似然概率P(xi​∣Y=y)表示在类别y下特征xi​取特定值的概率，根据特征类型采用不同计算方法。

​​离散特征​​：直接统计频率

P(xi​=v∣Y=y)=类别y的总样本数类别y中特征xi​取值为v的样本数​

​​示例​​：对于"是否包含'促销'字样"特征：

• 垃圾邮件中200封包含"促销"：
  P(xi​=包含’促销’∣Y=垃圾邮件)=300200​≈0.67
• 正常邮件中50封包含"促销"：
  P(xi​=包含’促销’∣Y=正常邮件)=70050​≈0.07

​​连续特征​​：通常假设服从高斯分布（正态分布），估计均值和方差：

​​示例​​：健康人群身高：

2.1.3 平滑处理（避免零概率问题）

当训练集中某特征值未出现在某类别中时，会导致似然概率为0，进而使整个后验概率为0。为解决这个问题，采用拉普拉斯平滑：

P(xi​=v∣Y=y)=类别y样本数+k计数+1​

其中k是该特征的可能取值数。

​​示例​​：正常邮件中无"免费"字样邮件（计数=0），k=2：

2.2 预测阶段

对新样本X，计算其属于各类别的后验概率：

1. 初始化：对于每个类别y，令score(y)=logP(y)
2. 特征贡献：对每个特征xi​，score(y)+=logP(xi​∣y)
3. 决策：选择score(y)最大的类别作为预测结果

​​示例​​：对新邮件（包含"促销"、大量图片链接、陌生发件人）：

• 垃圾邮件得分：
  log0.3+log0.67+logP(图片∣垃圾)+logP(陌生∣垃圾)

• 正常邮件得分：
  log0.7+log0.07+logP(图片∣正常)+logP(陌生∣正常)

比较两者得分，较高者决定邮件分类。

三、Python实例：鸢尾花案例

3.1案例背景：

本案例基于经典的​​鸢尾花数据集（Iris.scv）​​，包含100个样本，每个样本记录了鸢尾花的四个特征（花萼长度、花萼宽度、花瓣长度、花瓣宽度）和一个类别标签（0或1，代表两种鸢尾花品种）。通过​​朴素贝叶斯算法（MultinomialNB）​​，我们构建分类模型，根据花的形态特征预测其类别。代码实现了数据预处理、模型训练、混淆矩阵可视化等完整流程，最终评估模型在训练集和测试集上的分类性能。该案例适用于入门机器学习分类任务，特别适合演示特征与类别之间的概率关系建模。

3.2代码实现：

import pandas as pd#可视化混淆矩阵
def cm_plot(y,yp):from sklearn.metrics import confusion_matriximport matplotlib.pyplot as pltcm = confusion_matrix(y, yp)plt.matshow(cm, cmap=plt.cm.Blues)plt.colorbar()for x in range(len(cm)):for y in range(len(cm)):plt.annotate(cm[x,y],xy=(y,x),horizontalalignment='center',verticalalignment='center')plt.ylabel('True label')plt.xlabel('Predicted label')return plt"""
数据预处理
"""
data = pd.read_csv("iris.csv",header=None)#header=None代表读取的csv没有表头
data = data.drop(0, axis=1)#删除Id列#对原始数据集进行切分，
X_whole = data.drop(5, axis=1)#
y_whole = data[5]#"""切分数据集"""
from sklearn.model_selection import train_test_splitx_train_w, x_test_w, y_train_w, y_test_w = \train_test_split(X_whole, y_whole, test_size = 0.2, random_state = 0)from sklearn.naive_bayes import MultinomialNB#导入朴素贝叶斯分类器
#实例化贝叶斯分类器   分类， 中文识别分类。
classifier = MultinomialNB(alpha=1)
classifier.fit(x_train_w, y_train_w)#传入训练集数据"""训练集预测"""
#绘制训练集混淆矩阵
train_pred = classifier.predict(x_train_w)#自测cm_plot(y_train_w, train_pred).show()"""测试集预测"""
test_pred = classifier.predict(x_test_w)
cm_plot(y_test_w, test_pred).show()

3.3代码解析：

一、代码整体结构

这段代码实现了完整的机器学习分类流程：

1. 数据加载与预处理 → 2. 数据集划分 → 3. 模型训练 → 4. 结果评估

二、逐模块详解

1. 混淆矩阵可视化函数

def cm_plot(y, yp):from sklearn.metrics import confusion_matriximport matplotlib.pyplot as pltcm = confusion_matrix(y, yp)plt.matshow(cm, cmap=plt.cm.Blues)plt.colorbar()for x in range(len(cm)):for y in range(len(cm)):plt.annotate(cm[x,y], xy=(y,x), horizontalalignment='center',verticalalignment='center')plt.ylabel('True label')plt.xlabel('Predicted label')return plt

​​功能说明​​：

• 输入真实标签y和预测标签yp
• 生成热力图形式的混淆矩阵，颜色深浅表示数量多少
• 在矩阵每个单元格中央标注具体数值
• 添加坐标轴标签：纵轴为真实类别，横轴为预测类别

​​技术细节​​：

• confusion_matrix：计算分类结果的混淆矩阵
• matshow：矩阵可视化，使用蓝色渐变颜色映射
• annotate：在指定位置添加文本标注

2. 数据预处理

data = pd.read_csv("iris.csv", header=None)
data = data.drop(0, axis=1)
X_whole = data.drop(5, axis=1)
y_whole = data[5]

​​关键操作​​：

1. 读取无表头的CSV文件（header=None）
2. 删除第0列（序号ID列）
3. 划分特征和标签：
   • X_whole：包含第1-4列的特征矩阵
   • y_whole：第5列作为分类标签

3. 数据集划分

from sklearn.model_selection import train_test_split
x_train_w, x_test_w, y_train_w, y_test_w = \train_test_split(X_whole, y_whole, test_size=0.2, random_state=0)

​​参数说明​​：

• test_size=0.2：20%数据作为测试集
• random_state=0：固定随机种子保证结果可复现

​​最佳实践建议​​：

• 添加分层抽样保持类别比例：

  train_test_split(..., stratify=y_whole)

4. 模型训练

from sklearn.naive_bayes import MultinomialNB
classifier = MultinomialNB(alpha=1)
classifier.fit(x_train_w, y_train_w)

​​算法选择​​：

• MultinomialNB：适用于离散特征（如词频计数）的朴素贝叶斯实现
• alpha=1：拉普拉斯平滑系数，防止零概率问题

​​数学原理​​：
分类决策基于：

其中：

• P(y)：类别的先验概率
• P(xi​∣y)：特征xi​在类别y下的条件概率

5. 模型评估

# 训练集评估
train_pred = classifier.predict(x_train_w)
cm_plot(y_train_w, train_pred).show()# 测试集评估
test_pred = classifier.predict(x_test_w)
cm_plot(y_test_w, test_pred).show()

​​评估要点​​：

1. 训练集评估：检查模型学习能力
2. 测试集评估：验证模型泛化性能
3. 混淆矩阵解读：
   • 主对角线：正确分类的样本数
   • 其他位置：误分类情况

​​

三、完整流程图解

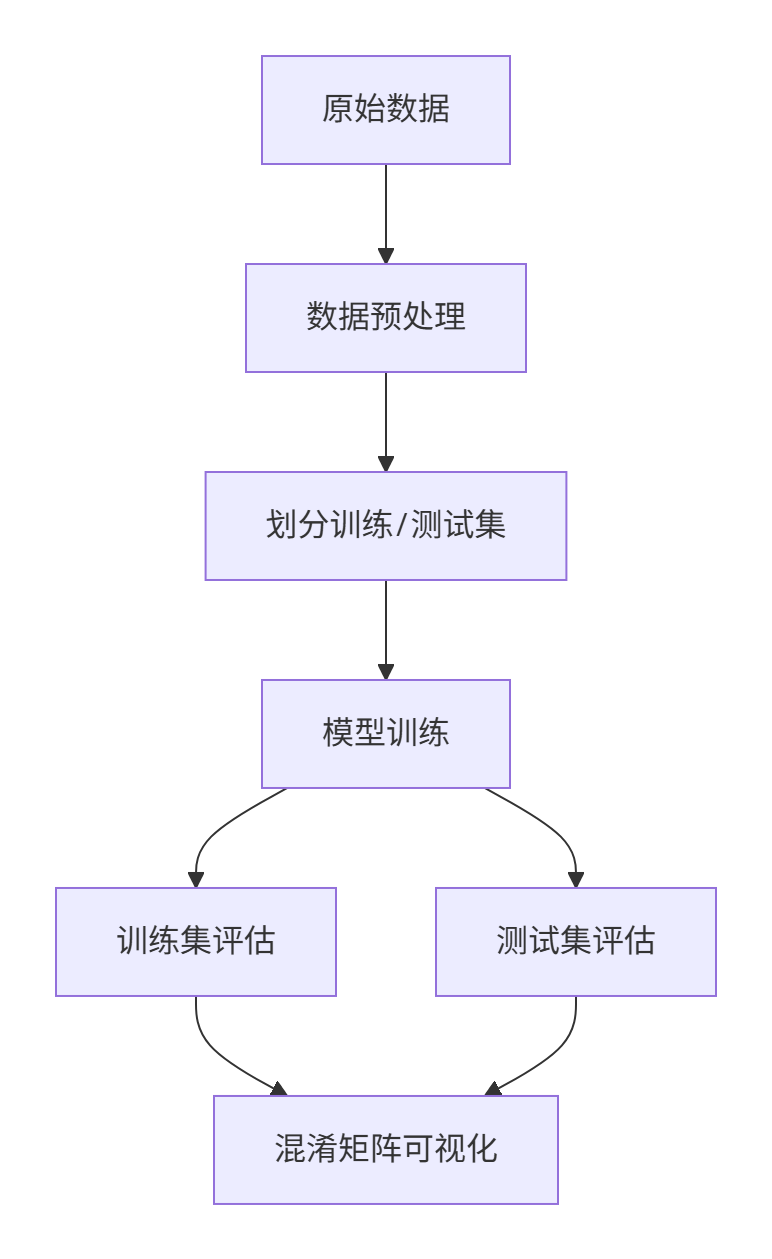
五、代码优化建议

1. ​​特征工程​​：

   from sklearn.feature_extraction.text import TfidfVectorizer
   vectorizer = TfidfVectorizer() # 创建TF-IDF向量化器
   X = vectorizer.fit_transform(text_data)

2. ​​超参数调优​​：

   from sklearn.model_selection import GridSearchCV
   params = {'alpha': [0.1, 1.0, 10.0]}
   grid = GridSearchCV(MultinomialNB(), param_grid=params, cv=5)
   grid.fit(X_train, y_train)

"朴素贝叶斯分类器特别适合高维文本数据，尽管条件独立性假设简单，但在实际应用中往往表现出色"
——《机器学习实战》，Peter Harrington

四、优缺点分析

4.1 优点

1. ​​计算高效​​：训练和预测时间复杂度低，适合大规模数据集和高维特征（如文本）。由于朴素贝叶斯基于条件独立性假设，将联合概率计算简化为多个边缘概率的乘积，在训练阶段只需对数据进行简单的统计计数，预测阶段的计算也主要是乘法和比较操作，无需复杂的迭代或矩阵运算，因此在处理大规模文本数据时，能够快速完成训练和预测任务。

2. ​​易于实现​​：原理直观，参数估计简单，无需复杂迭代优化。其核心理论贝叶斯定理和条件独立性假设易于理解，在实现过程中，计算先验概率和似然概率的方法直接明了，不需要像一些复杂模型那样进行大量超参数调整和复杂的优化算法，降低了开发和应用的门槛。

3. ​​对小样本友好​​：通过平滑处理可在小数据集上稳定工作。在小样本情况下，某些特征的统计可能不充分，容易出现零概率问题，但拉普拉斯平滑等技术能够对概率进行合理修正，使得模型在小样本数据上也能给出相对可靠的预测结果。

4. ​​可解释性强​​：每个特征对分类的贡献可通过概率直观体现。例如在垃圾邮件分类中，我们可以清楚地看到"促销""免费"等单词在垃圾邮件类别下的似然概率较高，说明这些特征对判断邮件为垃圾邮件有较大贡献，用户能够直观理解模型的决策依据。

4.2 缺点

1. ​​条件独立性假设局限​​：忽略特征间关联性，可能导致分类偏差（如"暴雨"和"洪水"的强关联被割裂）。在现实世界中，很多特征之间存在复杂的相互关系，而朴素贝叶斯的条件独立性假设忽视了这些关联。例如在自然灾害预测中，"暴雨"和"洪水"通常具有很强的关联性，但朴素贝叶斯会将它们视为独立特征，可能无法准确捕捉这种关系，从而影响对洪水发生概率的准确判断。

2. ​​对特征分布敏感​​：若实际分布与假设（如高斯分布）偏差较大，性能下降明显。以高斯朴素贝叶斯为例，如果连续特征的实际分布并非高斯分布，而是呈现出偏态分布或其他复杂分布，那么基于高斯分布假设计算的似然概率将不准确，导致整体分类性能降低。

3. ​​难以学习复杂模式​​：对非线性或高交互特征的建模能力较弱。朴素贝叶斯由于其简单的概率相乘模型结构，对于特征之间存在非线性关系或高维交互作用的情况，无法有效捕捉和建模，在处理这类复杂数据模式时表现不佳。

五、应用场景与变种

5.1 典型应用场景

1. ​​文本分类​​：垃圾邮件过滤、新闻分类、情感分析等
2. ​​推荐系统​​：基于内容的推荐、协同过滤的补充
3. ​​医疗诊断​​：症状与疾病的概率关系建模
4. ​​实时系统​​：需要快速响应的在线分类任务

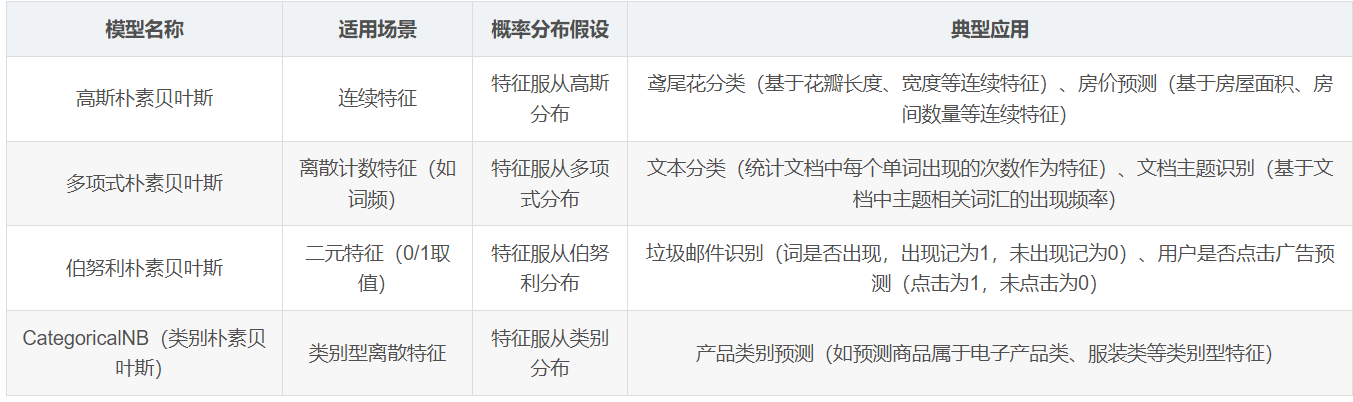
5.2 常见变种

1. ​​高斯朴素贝叶斯​​：假设连续特征服从高斯分布
2. ​​多项式朴素贝叶斯​​：适用于离散特征和计数数据（如文本词频）
3. ​​伯努利朴素贝叶斯​​：针对二值特征（如文本中的单词是否出现）
4. ​​类别朴素贝叶斯​​：改进小样本情况下的概率估计

结语

朴素贝叶斯算法以其简单高效的特点，在机器学习领域占据重要地位。尽管其"朴素"的独立性假设看似过于简化，但在许多实际应用中表现出乎意料的好。理解其核心原理和实现细节，不仅有助于我们正确应用这一算法，更能为理解更复杂的概率图模型奠定基础。在实践中，建议通过特征选择、适当的分布假设和超参数调优来提升模型性能，使其在特定任务中发挥最大效用。