当前位置：首页 > news >正文

贪心算法

news 2025/8/5 9:30:23

一、贪心算法概述

贪心算法是一种通过局部最优选择来达到全局最优解的算法设计方法。它从问题的初始状态出发，通过一系列贪心选择来得出最优值或较优解。

核心思想：每一步都做出当前看起来最佳的选择，而不考虑整体情况。

二、贪心算法的基本特性

1. 贪心选择性质

将原问题转化为相似的但规模更小的子问题
每一步的选择都依赖于已做出的选择，但不依赖于未做的选择
当前的选择是局部最优的

2. 最优子结构性质

问题的最优解包含其子问题的最优解
算法中每一次都取得局部最优解
全局最优解由一系列局部最优解组成

三、贪心算法经典问题

1. 最优装载问题

问题描述：给定n个物体，第i个物体重量为wi，选择尽量多的物体，使总重量不超过C。

贪心策略：先装最轻的物体。

2. 部分背包问题

问题描述：有n个物体，第i个物体重量为wi，价值为vi，在总重量不超过C的情况下让总价值尽量高。每个物体可以只取一部分。

贪心策略：按单位重量价值(vi/wi)从高到低选择。

3. 乘船问题

问题描述：有n个人，第i个人重量为wi。每艘船载重量为C，最多乘两人。用最少的船装载所有人。

贪心策略：最轻的人和最重的人配对。

四、贪心算法的高级应用

1. 选择不相交区间问题

问题描述：给定n个开区间(ai,bi)，选择尽可能多的区间，使这些区间两两没有公共点。

算法步骤：

按结束时间bi从小到大排序
依次考虑各个区间，如果不与已选区间冲突，则选择

2. 区间选点问题

问题描述：给定n个闭区间[ai,bi]，在数轴上选尽量少的点，使每个区间内至少有一个点。

算法步骤：

按结束位置从小到大排序
对于当前区间，若集合中的点不能覆盖它，则将区间末尾的点加入集合

3. 区间覆盖问题

问题描述：给定n个闭区间[ai,bi]，选择尽量少的区间覆盖指定线段[s,t]。

算法步骤：

按左端点从小到大排序
每次选择覆盖点s的区间中右端点最大的一个
将s更新为该区间的右端点
重复直到覆盖整个线段

4. 流水作业调度问题

问题描述：n个产品需先在A车间加工(时间ai)，后在B车间加工(时间bi)。安排加工顺序使总时间最短。

算法步骤：

计算Mi = min{ai, bi}
将M按从小到大排序
若Mi=ai，排在前部；若Mi=bi，排在后部

5. 带限期和罚款的任务调度

问题描述：n个任务，每个需1单位时间执行，任务i有截止时间di和罚款wi。安排顺序使总罚款最小。

算法步骤：

按罚款wi从大到小排序
为每个任务安排最靠后的可用时间
若无可用时间，则放弃该任务

五、贪心算法的适用条件

问题具有贪心选择性质
问题具有最优子结构性质
局部最优解能导致全局最优解

六、贪心算法的局限性

不能保证对所有问题都得到最优解
需要证明其正确性
对某些问题可能得到近似解而非精确解

七、贪心算法设计步骤

建立数学模型描述问题
将问题分解为若干子问题
确定贪心策略，得到局部最优解
将局部最优解合并为全局解
证明算法的正确性

八、习题训练

淘淘捡西瓜

描述

地上有一排西瓜，每个西瓜都有自己的重量。淘淘有一个包，包的容量是固定的，淘淘希望尽可能在包里装更多的西瓜（当然要装整个的，不能切开装），请问淘淘的包最多能装下多少个西瓜？

输入描述

第一行两个整数n，x，表示有n个西瓜，背包容量是x。（1<=n<=100）
下面n个整数数，表示西瓜的重量。

输出描述

一个整数，表示淘淘最多能装多少西瓜回家。

用例输入 1

5 10
2 3 1 5 4

用例输出 1

#include <bits/stdc++.h>
using namespace std;
int n,x,a[101],ans;
int main() {cin>>n>>x;for(int i=1; i<=n; i++) cin>>a[i];sort(a,a+n+1);for(int i=1; i<=n; i++) {if(a[i]<=x) {ans++;x-=a[i];}}cout<<ans;return 0;
}

任务调度

描述

乌龟因为动作太慢，有 n 个任务已经超过截止日期了。乌龟处理第 i 个任务需要 ai 单位时间。从 0 时刻开始，乌龟可以选择某项任务，完成它，然后再开始另一项任务，如此往复直到所有任务都被完成。

由于已经超过截止日期，乌龟会为此受到一定的惩罚，惩罚值等于所有任务完成时刻之和。例如，有 2 个任务分别需要 10 和 20 单位时间完成。如果先完成任务 1，惩罚值为 10 + 30 = 40；如果先完成任务 2，惩罚值为 20 + 30 = 50。
乌龟希望你求出惩罚值最小的完成任务的顺序。

输入描述

两个整数 n, R1，表示任务的数量和生成数列的首项。处理任务 i (1 i n) 的时间 ai = (Ri mod 100) + 1。

试题中使用的生成数列 R 定义如下：整数 0 ≤ R1 < 20170 在输入中给出。对于 i > 1，Ri = (Ri−1 × 6807 + 2831) mod 20170。

输出描述

一个整数，表示完成所有任务的最小惩罚值

用例输入 1

10 2

用例输出 1

1771

提示

数据规模
1 ≤ n ≤ 100000

来源
2017江苏省青少年信息学奥林匹克竞赛复赛

#include <bits/stdc++.h>
using namespace std;long long a[100010], r[100010];
long long  n, ans, tot;
int main() {cin >> n >> r[1];for (int i = 1; i <= n; ++i) {a[i] = (r[i] % 100) + 1;r[i + 1] = (r[i] * 6807 + 2831) % 20170;}sort(a + 1, a + n + 1);for (int i = 1; i <= n; ++i) {tot += a[i];ans += tot;}cout << ans << endl;return 0;
}

买木头

描述

有n个木材供应商（1≤n≤10000），每个供货商有长度相同一定数量的木头。长木头可以锯短，但短木头不能接长。有一个客人要求m根长度相同的木头。
要求计算出，此时供货商提供的木头满足客人要求的最长的长度是多少。
例如n=2,m=30，两个供货商的木头为：
12,10 第1个供货商的木头长度为12，共有10根
5,10 第2个供货商的木头长度为5，共有10根。
计算的结果为5，即长度为12的木头一根可锯出两根长度为5的木头，多余的无用，长度为5的木头不动，此时可得到30根长度为5的木头。

输入描述

整数n,m,l1,s1（1≤m≤1000000,1≤l_1≤10000,1≤s_1≤100）
其中l1是第一个供货商木头的长，s1是第一个供货商木头数量。其他供货商木头的长度和数量li和si（i≥2），由下面的公式给出：
li=((l(i-1)×37011+10193) mod 10000)+1
si=((s(i-1)×73011+24793) mod 100)+1

输出描述

一个整数，即满足要求的m根长度相同的木头的最大长度。

用例输入 1

10 10000 8 20

用例输出 1

201

来源

省赛数组问题二维数组结构体

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a[100010], b[100010];int main(){ios :: sync_with_stdio(0);	// 提高cin、cout的运行速度ll n, m, l, s;cin >> n >> m >> l >> s;ll maxn = l;a[1] = l;b[1] = s;for(int i = 2; i <= n; i++){a[i] = ((a[i - 1] * 37011 + 10193) % 10000) + 1;b[i] = ((b[i - 1] * 73011 + 24793) % 100) + 1;maxn = max(a[i], maxn);}for(ll i = maxn; i >= 1; i--){    // 从最大的木头长度开始找ll sum = 0;                   // 当前长度能砍的树为0for(int j = 1; j <= n; j++){sum += (a[j] / i) * b[j];        // 遍历所有可以砍的组合}if(sum >= m){                        // 如果足够输出并退出cout << i << endl;return 0;}}return 0;
}

[NOIP2007 普及组] 纪念品分组

描述

元旦快到了，校学生会让乐乐负责新年晚会的纪念品发放工作。为使得参加晚会的同学所获得的纪念品价值相对均衡，他要把购来的纪念品根据价格进行分组，但每组最多只能包括两件纪念品，并且每组纪念品的价格之和不能超过一个给定的整数。为了保证在尽量短的时间内发完所有纪念品，乐乐希望分组的数目最少。
你的任务是写一个程序，找出所有分组方案中分组数最少的一种，输出最少的分组数目。

输入描述

共n＋2行:
第一行包括一个整数w，为每组纪念品价格之和的上限。
第二行为一个整数n，表示购来的纪念品的总件数G。
第3 n＋2行每行包含一个正整数P表示所对应纪念品的价格。
50%的数据满足:1≤n≤15。
100%的数据满足:1<n≤3×104,80<w≤200，5≤Pi≤w。

输出描述

一个整数，即最少的分组数目。

用例输入 1

用例输出 1

#include <bits/stdc++.h>
using namespace std;
int main() {int w, n;cin >> w >> n; // 输入每组价格上限和纪念品数量int prices[n];for (int i = 0; i < n; i++) {cin >> prices[i]; // 输入每件纪念品的价格}sort(prices, prices + n); // 排序int i = 0, j = n - 1, groups = 0;while (i <= j) {if (prices[i] + prices[j] <= w) {i++; // 可以配对}j--; // 最大价格的指针向左移动groups++; // 形成一组}cout << groups << endl; // 输出最少的分组数return 0;
}

【提高】拦截导弹的系统数量求解

描述

某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。

假设某天雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。

输入n个导弹依次飞来的高度（给出的高度数据是不大于30000的正整数），计算如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
比如：有8颗导弹，飞来的高度分别为
389 207 175 300 299 170 158 165
那么需要2个系统来拦截，他们能够拦截的导弹最优解分别是：
系统1：拦截 389 207 175 170 158
系统2：拦截 300 299 165

输入描述

两行，第一行表示飞来导弹的数量n（n<=1000）
第二行表示n颗依次飞来的导弹高度

输出描述

要拦截所有导弹最小配备的系统数k

用例输入 1

8
389  207  175  300  299  170  158  165

用例输出 1

来源

贪心

#include<bits/stdc++.h>
using namespace std;
//x：代表每个导弹的高度
//p：找到的能拦截导弹的系统的下标
//k：a数组中已有的能够拦截导弹的系统数量
int a[1010],i,n,x,p,k,j;
int main() {cin>>n;for(i=1; i<=n; i++) {cin>>x;p=-1;//循环a数组，找到第一个能够拦截的系统for(j=1; j<=k; j++) {if(a[j]>=x) {p=j;break;}}//如果没找到系统拦截if(p==-1) {k++;a[k]=x;//设定新系统能拦截的最高高度} else {//用第p个系统拦截，修改系统的最高高度a[p]=x;}}cout<<k;return 0;
}

【NOIP2010 入门】导弹拦截

描述

经过11年的韬光养晦，某国研发出了一种新的导弹拦截系统，凡是与它的距离不超过其工作半径的导弹都能够被它成功拦截。当工作半径为0时，则能够拦截与它位置恰好相同的导弹。但该导弹拦截系统也存在这样的缺陷：每套系统每天只能设定一次工作半径。而当天的使用代价，就是所有系统工作半径的平方和。

某天，雷达捕捉到敌国的导弹来袭。由于该系统尚处于试验阶段，所以只有两套系统投入工作。如果现在的要求是拦截所有的导弹，请计算这一天的最小使用代价。

【提示】
两个点(x1, y1)、(x2, y2)之间距离的平方是(x1− x2)2+(y1−y2)2。
两套系统工作半径r1、r2 的平方和，是指r1、r2 分别取平方后再求和，即r12+r22。

输入描述

第一行包含4 个整数x1、y1、x2、y2，每两个整数之间用一个空格隔开，表示这两套导弹拦截系统的坐标分别为(x1,y1)、(x2,y2)。
第二行包含1个整数N，表示有N 颗导弹。接下来N行，每行两个整数x、y，中间用一个空格隔开，表示一颗导弹的坐标(x, y)。不同导弹的坐标可能相同。

输出描述

输出只有一行，包含一个整数，即当天的最小使用代价。

用例输入 1

用例输出 1

提示

输入样例#1：
0 0 10 0
2
-3 3
10 0
输出样例#1：
18
输入样例#2：
0 0 6 0
5
-4 -2
-2 3
4 0
6 -2
9 1
输出样例#2：
30
【样例1说明】
样例1中要拦截所有导弹，在满足最小使用代价的前提下，两套系统工作半径的平方分别为18和0。
【样例2说明】
样例中的导弹拦截系统和导弹所在的位置如下图所示。要拦截所有导弹，在满足最小使用代价的前提下，两套系统工作半径的平方分别为20和10。

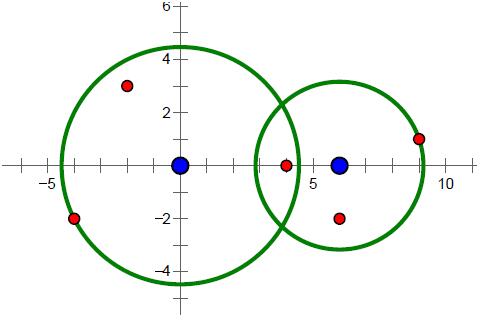
【数据范围】
对于10%的数据，N = 1
对于20%的数据，1 ≤ N ≤ 2
对于40%的数据，1 ≤ N ≤ 100
对于70%的数据，1 ≤ N ≤ 1000
对于100%的数据，1 ≤ N ≤ 100000，且所有坐标分量的绝对值都不超过1000。
【来源】
noip2010普及组第3题。

来源

noip复赛

#include <bits/stdc++.h>
using namespace std;const int N = 100005;
struct node
{int s1, s2;
};
node w[N];
int X1, Y1, X2, Y2, n;bool cmp(node a, node b)
{return a.s1 > b.s1;
}int main()
{cin >> X1 >> Y1 >> X2 >> Y2 >> n;int x, y;for(int i = 1; i <= n; i++){cin >> x >> y;w[i].s1 = (x - X1) * (x - X1) + (y - Y1) * (y - Y1);w[i].s2 = (x - X2) * (x - X2) + (y - Y2) * (y - Y2);}sort(w + 1, w + n + 1, cmp);int r1 = 0; //拦截系统1的最小半径int r2 = 0; //拦截系统2的最小半径int ans = INT_MAX; //r1 + r2for(int i = 0; i <= n; i++) //注意从0开始可以处理一开始全归属系统1{r1 = w[i+1].s1; //把i归属给拦截系统2，拦截系统1的半径更新r2 = max(r2, w[i].s2); //拦截系统2的最小半径更新，每次归属的导弹取较大值ans = min(ans, r1 + r2);}cout << ans;return 0;
}

查看全文

http://www.dtcms.com/a/314745.html