PEAFOWL-IEEE-2025

1. 本文是对原论文学习过程中的中文翻译，仅用于学术交流与科普分享，无任何商业目的。
2. 翻译已尽力忠实原文，但受限于译者水平，可能存在偏差；术语或公式若有疑义，请以原文为准。
3. 若原作者、期刊或版权方提出异议，译者将在收到通知后 24 小时内删除本文并致歉。
4. 欢迎读者引用原文，并请注明出处

Peafowl: Private Entity Alignment in Multi-Party Privacy-Preserving Machine Learning

PEAFOWL：多方隐私保护机器学习中的私有实体对齐协议
Ying Gao; Huanghao Deng; Zukun Zhu; Xiaofeng Chen; Yuxin Xie; Pei Duan

摘要——在纵向分布式数据的隐私保护机器学习中，私有实体对齐方法用于安全匹配并利用相同样本的特征。然而现有方法不仅存在暴露样本交集和引入不必要样本的风险，还面临适应多方场景的局限性。为此我们提出PEAFOWL——一种创新的多方私有实体对齐协议。该方法通过原始数据集到交集的映射（称为置换）实现多方实体对齐，避免直接使用交集从而缓解交集泄露与样本冗余问题。该协议利用云服务器执行秘密共享混洗来保护置换隐私性，防止数据提供方共谋重建交集。进一步结合种子同态伪随机生成器，PEAFOWL避免了秘密共享的高通信开销，获得卓越的运行时性能。此外通过预计算置换操作引入离线/在线变体，确保通信与计算复杂度相对数据集规模呈线性增长。在实际PPML框架中的实施表明，该协议在多种多方场景下均具有实用效能。实验显示PEAFOWL的开销不足训练总成本的$1\%$，而离线/在线变体可降低约$50\%$的在线运行时长。总体而言，PEAFOWL为多方PPML提供了高效简洁的解决方案，极具实施与改进潜力。

一、引言

隐私保护机器学习（PPML）已成为在保持数据机密性的同时分析分布式数据集的重要技术。该技术融合差分隐私、同态加密和可信执行环境等方法，其中安全多方计算（MPC）通过秘密共享（SS）等密码协议使多方能联合计算函数输出而不泄露各自输入数据，成为该领域核心技术。基于SS的PPML框架如Falcon、CrypTFlow和CrypTen相继问世，这些框架要求在模型训练前完成多方间的安全数据共享。

但这一安全共享过程面临现实挑战。典型的PPML应用涉及纵向分区数据集上的模型训练，各方持有相同样本（实体）的不同特征子集。例如不同专科医院可能拥有相同患者（样本）的不同体检结果（特征）。通常这些参与方的样本空间并不完全重合，导致难以直接对所有样本实施SS。因此需要额外的对齐阶段来识别共有实体并安全共享对应特征，即实体对齐。许多PPML研究使用样本ID等可识别信息进行跨数据集实体匹配，但直接使用此类信息可能导致ID及非共享实体数据的泄露风险。

为降低敏感信息泄露风险，私有实体对齐技术日益受到关注。私有集合交集（PSI）被广泛用于此场景，使各方能计算数据集交集而不泄露其他元素，随后仅共享交集中样本的特征用于模型训练的MPC协议。但PSI仍会向所有参与方披露交集信息。现实中这可能暴露个人行为轨迹，进而推断其社交关系与个人偏好。如图1所示，假设多家医疗机构与保险公司合作开发基于病史的个性化保险方案，使用PSI识别共同患者或客户时，会无意泄露数据集的交集信息。保险公司通过知晓交集成员，可推断哪些人正在特定医疗科室就诊，这可能暗示精神疾病或HIV/AIDS等敏感状况，进而影响个人的保险费用或就业机会。

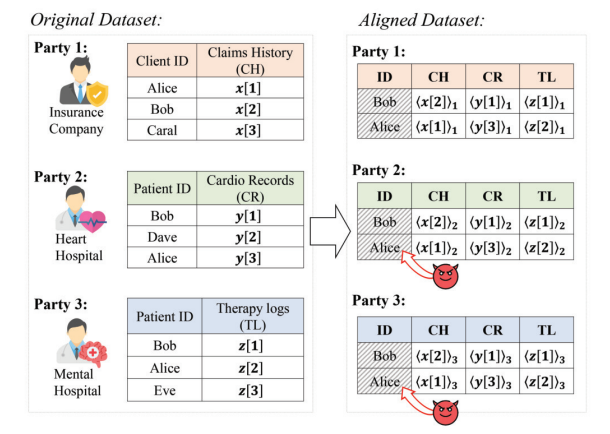
图1. 隐私实体对齐示例

近期研究致力于通过保护交集信息来增强基于PSI方法的隐私性，但这些研究主要针对双方场景。其中一种方法是在交集结果中添加混淆元素以防止参与方完全识别交集元素，例如非对称PSI（APSI）向一方结果引入混淆元素，而基于隐私集合并（PSU）的方法则用并集替代交集作为结果，这两种方式都会在对齐结果中引入误差。另一种方法采用基于电路的PSI（CPSI）协议，以安全无误差的秘密共享格式输出交集结果和特征份额，避免影响PPML训练。虽然也可以基于通用MPC架构构建方法，但这可能带来显著开销。然而这些协议存在两个共性问题：1）由于混淆元素过多或密码学组件限制，难以从双方场景扩展到多方场景；2）包含冗余的非交集样本会增加训练或去冗余的计算成本，特别是在处理高维特征时。这些缺陷限制了它们在多方PPML中的应用。

为实现多方间安全高效的隐私实体对齐，我们设计了一种名为PEAFOWL的新型PPML协议。该协议采用基于置换的机制将数据集对齐至交集，避免交集信息泄露并消除样本冗余。我们引入外包云服务器辅助该过程：服务器在不知晓参与方原始数据集的情况下计算置换参数，随后参与方利用服务器对秘密共享数据进行置换对齐而无需知晓置换规则。为确保PEAFOWL的安全性与效率，我们采用秘密共享洗牌技术和种子同态伪随机生成器，既防止置换信息泄露给数据提供方，又避免共享高维特征数据带来的巨大开销，从而提升传输效率。此外，我们还设计了离线/在线变体，通过特殊构造的秘密共享洗牌方案离线处理复杂置换，降低在线通信成本。

我们的主要贡献如下：

1. 据我们所知，这是首次在第三节明确定义的多方隐私实体对齐场景中解决交集泄露问题。我们提出的基于置换的机制能安全对齐多方数据，缓解传统方法固有的交集泄露和样本冗余问题。

2. 我们提出了一种新型协议，在半诚实模型下仅暴露交集基数即可确保安全性。该协议在高维数据库和大量参与方场景下表现优异。

3. 我们设计了该协议的离线/在线变体以最小化在线通信和计算开销。该变体通过预计算部分置换参数，使通信和计算复杂度随数据集规模呈线性增长。

4. 我们通过多方场景实验实证验证了系统的实际可行性。在开源PPML框架中实现的PEAFOWL系统展现出极低开销，相比训练阶段成本仅增加约$1\%$。

二、相关工作

A. 隐私集合求交

PSI是一种密码学协议，用于识别两个（或多个）集合中的共有元素而不泄露非共有元素信息。但大多数PSI实现方案直接输出计算结果，这会破坏隐私。如第一节所述，现有解决交集泄露的方案主要分为两种策略。

1. 添加混淆元素：He等人提出APSI协议，通过向交集添加混淆元素来防止样本较少方的样本ID信息泄露。该策略保护弱势方样本但仅保障单方，不适用于隐私实体对齐。Wei等人采用PSU协议安全识别样本并集，为PPML输出并集而非交集。该方法通过包含所有元素来模糊交集，但由于非交集样本特征不可用，需使用生成对抗网络(GAN)合成特征和标签，导致显著数据集冗余。该方案可通过多方PSU扩展至多方场景，但存在计算并集的高成本及GAN生成合成特征对训练的潜在影响等缺陷。

2. 电路PSI：CPSI协议以秘密共享格式安全输出交集结果和特征信息而不泄露交集细节。其输出样本均含二元指示符(1或0)标记交集状态，所有样本特征数据（包括非交集冗余样本）在参与方间秘密共享。因此后续模型训练需对所有样本进行高成本的安全比较电路运算以确定交集状态及特征是否纳入训练。安全计算PSI协议作为潜在解决方案，虽输出专用于交集的函数，但仍需对非交集元素进行电路计算，考虑特征时还需大量电路操作。iPrivJoin框架通过茫然混淆技术模糊结果后重构指示符来剔除非交集样本，虽减少冗余样本但不支持多方场景，且需额外计算通信资源（如为避免布谷鸟哈希算法误报需生成1.4倍无效扩展）。将这些基于CPSI的方法扩展至多方场景具有挑战性——多数电路PSI的多方扩展方案不适用于附加特征数据，这些特征必须与ID绑定并在电路中计算，导致高计算成本和非交集元素冗余。此外iPrivJoin采用含随机性的布谷鸟哈希表存储样本，导致交集顺序不确定，多次执行双方协议也无法对齐结果。

其他方法也保护交集隐私，如Openvfl[30]采用标记PSI仅公开特征信息，并利用同态加密进行安全计算。但该方案限于双方场景，无法直接扩展至带标签的多方PSI(MPSI)。与本文聚焦秘密共享(SS)以兼容现有MPC框架不同，Openvfl需针对同态加密额外设计纵向联邦学习方案。

B. 隐私保护机器学习

PPML是机器学习中保护训练推理过程敏感数据安全的重要领域。主流方案采用多方计算技术(MPC)，这些技术用于训练通过本方法或其他方法获得的对齐共享数据集。已有大量基于MPC的PPML工作如Astra、Falcon、CrypTFlow和CrypTen等，多数框架基于最轻量级的MPC原语——算术秘密共享构建，该技术在隐私保护方面灵活性高且效率突出，但通信开销较大，部分原因是乘法运算需特定密码学构件且常需第三方协助生成。

三、预备知识与问题陈述

本节简要描述PEAFOWL系统中使用的密码学工具基础，并形式化定义待解决问题。表I汇总了常用符号说明。

A. 算术秘密共享

算术秘密共享将标量值$x\in {\mathbb{R}}_Q$在参与方$P_i\left(i\in \left[N\right]\right)$之间分配，其中${\mathbb{R}}_Q$表示具有$Q$个元素的环。通过构造份额{⟨x⟩i}i∈[N]{\left\{ \langle x{\rangle }_{i}\right\} }_{i \in \left\lbrack N\right\rbrack }{⟨x⟩i​}i∈[N]​（其中$⟨x{⟩}_i\in {\mathbb{R}}_Q$）使其总和能重构原始值$x$，表示为$x=\sum _{i\in \left[N\right]}⟨x{⟩}_i$。实现共享时，参与方通常生成由$N$个随机数组成的伪随机零份额，这些随机数总和为零。随后，持有$x$的参与方将该值加入其份额后销毁原值。本工作中，我们在${\mathbb{Z}}_{2^{\ell }}$采用算术秘密共享，并参照前人工作使用定点编码将浮点值$x_R$转换为目标整型$x$。该编码过程需将$x_R$乘以大比例因子$B$后四舍五入：$x=\lceil x_R\rfloor$，其中$B=2^L$且$L$表示比特精度。解码时计算$x_R\approx x/B$。参数取值参考设定为$\ell =64$和$L=16$。

B. 种子同态伪随机生成器

设固定群${\mathbb{G}}_s$和${\mathbb{G}}_y$分别配备运算$\oplus$和$\otimes$。种子同态伪随机生成器(SHPRG)是多项式时间算法$\mathcal{G}$：${\mathbb{G}}_s\to {\mathbb{G}}_y$，具有以下特性：

图2. 置换共享理想功能${\mathcal{F}}_{ps}$

• 伪随机性：$\mathcal{G}$作为伪随机生成器（PRG），满足$\left|{\mathbb{G}}_s\right|<\left|{\mathbb{G}}_y\right|$，其输出在计算上与随机序列不可区分。

• 种子同态性：对所有$s_1,s_2\in {\mathbb{G}}_s$，存在$\mathcal{G}(s_1\oplus$$s_2)=\mathcal{G}\left(s_1\right)\otimes \mathcal{G}\left(s_2\right)$。

我们的工作采用基于舍入学习问题（LWR）构建的伪随机生成器。给定满足$p<q$和$d<m$的公共参数$d,m,p,q$，伪随机生成器$\mathcal{G}\left(s\right):{\mathbb{Z}}_q^d\to {\mathbb{Z}}_p^m$定义如下：

$$\mathcal{G}\left(s\right)={\lceil {\mathbf{A}}^{\top }\cdot s\rfloor }_p.\text{\hspace{1em}(1)}$$

此处$\mathbf{A}$是从${\mathbb{Z}}_q^{d\times m},s$随机采样的另一个公共参数，${\mathbb{Z}}_q^d$均匀选自$\lceil \cdot {\rfloor }_p$，对于$x\in {\mathbb{Z}}_q$定义$\lceil x{\rfloor }_p=\lceil x\cdot p/q\rfloor$。虽然该伪随机生成器不严格具备种子同态性，但在以下意义上近似：

$$\mathcal{G}\left(s_1+s_2\right)=\mathcal{G}\left(s_1\right)+\mathcal{G}\left(s_2\right)+e,\text{\hspace{1em}(2)}$$

误差项为e∈{−1,0,1}me \in \{ - 1,0,1{\} }^{m}e∈{−1,0,1}m。该函数近乎种子同态，足够接近且适用于我们的应用场景。注意SHPRG的安全性依赖于${\mathrm{LWR}}_{d,q,p}$问题的困难性。$1/p$的取值与容错学习中的错误率$\alpha$成正比，因此参数选择需确保${\mathrm{LWE}}_{d,q,1/p}$足够困难以满足安全等级要求。

C. 混洗构建模块

我们重述文献定义的主要密码学工具，包括置换共享（Permute+Share）和份额转换（Share Translation）。

置换共享：如图2所示，功能${\mathcal{F}}_{ps}$使双方能对输入进行混洗和共享。本方案中，一方提供置换$\pi$作为输入，另一方提供${\mathbb{Z}}_{2^{\xi }}$中的元素集$x$作为输入$\mathbf{x}$。输出为置换后元素$\pi \left(\mathbf{x}\right)$的秘密份额。${\mathcal{F}}_{ps}$的目标是让双方获得份额的同时不泄露对方输入信息，即满足以下安全保证：

• 置换隐藏性：对所有$\pi ,{\pi }^{\prime }\in {\Pi }_{\left[n\right]}$，${\mathcal{F}}_{ps}\left(\pi ,\mathbf{x}\right)$与${\mathcal{F}}_{ps}\left({\pi }^{\prime },\mathbf{x}\right)$的视图不可区分

• 份额隐藏性：对任意$\mathbf{x},{\mathbf{x}}^{\prime }\in {\mathbb{Z}}_{2^{\xi }}^n$，${\mathcal{F}}_{ps}\left(\pi ,\mathbf{x}\right)$与${\mathcal{F}}_{ps}\left(\pi ,{\mathbf{x}}^{\prime }\right)$的视图不可区分

如文献[27]所述，先前的研究如[14]和[37]也可用于安全实现${\mathcal{F}}_{ps}$。所有这些方案的计算/通信复杂度均为$\mathcal{O}\left(n\log n\right)$。

图3. 共享转换理想功能${\mathcal{F}}_{st}$。

共享转换：该功能${\mathcal{F}}_{st}$可视为${\mathcal{F}}_{ps}$协议的变体，其中数据$\mathbf{x}$由协议伪随机选择而非受参与方控制。如图3所示，一方输入$\pi$，另一方无输入。输出结果为$\mathbf{\Delta }$及(a,b)对，其中$\mathbf{\Delta },\mathbf{a}$，且$\mathbf{b}$是${\mathbb{Z}}_{2^{\xi }}$中具有$n$个元素的向量。该协议还需满足Permute+Share中规定的安全保证，并确保以下正确性：

• 正确性：对于每个$\pi \in {\Pi }_{\left[n\right]}$，令$\left(\mathbf{\Delta },\left(\mathbf{a},\mathbf{b}\right)\right)\leftarrow {\mathcal{F}}_{st}\left(\pi ,\perp \right)$，需满足$\mathbf{b}=\pi \left(\mathbf{a}\right)-\mathbf{\Delta }$。

D. 问题表述

如前所述，私有实体对齐旨在多方参与PPML前对齐数据集而不暴露样本交集。针对此问题，我们考虑一个包含$N$个参与方$P_1,P_2,\cdots ,P_N$及外包云服务器$\mathcal{S}$的场景。每个参与方$P_i$持有来自未对齐数据集的独特样本序列，记为Di={Ii,Xi}{\mathbf{D}}_{i} = \left\{ {{\mathbf{I}}_{i},{\mathbf{X}}_{i}}\right\}Di​={Ii​,Xi​}。此处${\mathbf{I}}_i\left[u\right]$表示分配给第$u$个样本的唯一标识符（称为ID），我们假设每个标识符${\mathbf{I}}_i\left[u\right]$在${\mathbf{I}}_i$中唯一。相应地，${\mathbf{X}}_i\left[u\right]$表示参与方$P_i$中与${\mathbf{I}}_i\left[u\right]$关联的数据元素（称为特征）。

各方均旨在借助外包服务器的协助获取对齐数据集中各自的份额。该对齐数据集由各方的交集样本构成，其中各参与方的特征按既定顺序进行拼接。形式上，每个参与方$P_i$需计算对齐数据集特征${\mathbf{X}}_A$的份额${⟨{\mathbf{X}}_A⟩}_i$，其计算方式如下：

$${\mathbf{X}}_A=\left\{\prod _{i\in \left[\mathbb{N}\right]}{\mathbf{X}}_i\left[u_i\right]\mid {\mathbf{I}}_1\left[u_1\right]={\mathbf{I}}_2\left[u_2\right]=\cdots ={\mathbf{I}}_3\left[u_N\right]\in \bigcap _{i\in \left[\mathbb{N}\right]}{\mathbf{I}}_i\right\}.(3)$$

值得注意的是，该问题与基于电路的MPSI不同，后者共享的是ID交集而非特征交集。

我们采用"诚实但好奇"的威胁模型，假设服务器与参与方均遵循协议但可能窥探数据。在此模型中，假定最多有$T\le N-1$个（共$N$个）参与方可能共谋获取其余$N-T$方的信息，并默认服务器不与任何参与方勾结。该假设已被多数MPC框架及PSI研究采纳。

我们的目标是设计一个满足正确性与隐私性的实体对齐协议，具体指标定义如下：

• 正确性：对齐协议必须以可忽略的误差为各方$P_i$生成PPML所需的共享格式${⟨{\mathbf{X}}_A⟩}_i$输出。

• 隐私性：对齐协议应保护每个$P_i$及$\mathcal{S}$的数据集交集与特征隐私。

在后续实现中，本方案提供高效的服务器辅助方法但会暴露交集基数。实践中这种泄露通常可接受，尤其相较于暴露完整交集的情形。此外，通过过滤非交集元素获得的效率提升更为显著。

四、协议设计

本节正式介绍多方场景下的隐私实体对齐协议及其离线/在线变体方案。

A.核心机制：基于排列的解决方案

基于现有方法分析，最常用的$mPSI+$共享方案实现对齐的方式如下：

1. 各方$P_i$执行多方PSI协议获取ID交集${\mathbf{I}}_A\leftarrow {\cap }_{i\in \left[N\right]}{\mathbf{I}}_i$

2. 参与方$P_i$根据${\mathbf{I}}_A$中的ID筛选数据集${\mathbf{D}}_i$，随后共享并拼接特征数据${⟨{\mathbf{X}}_i⟩}_j,j\in \left[N\right]$

但该方案本质上会泄露交集${\mathbf{I}}_A$的隐私，因所有参与方必须共享交集集合。我们提出创新性解决方案，其核心洞见在于：隐私实体对齐并不要求各方完全知晓交集内容，只需知道各自数据集中应保留的样本位置及排列顺序即可构建对齐数据集。如图1所示，$P_1$数据库中第二与第一元素{2,1}\{ 2,1\}{2,1}构成交集${\mathbf{I}}_A=${\{{Bob,Alice$\}$。同理，$P_2$的集合{1,3}\{ 1,3\}{1,3}与$P_3$的集合{1,2}\{ 1,2\}{1,2}也表征相同交集。各方通过知晓交集元素位置即可识别交集，而其余元素的映射位置可视为排列$\pi \in {\Pi }_{\left[n\right]}$——其中前$n_A$个（交集基数）映射元素即构成交集。这些排列足以确定需保留的样本及特征拼接顺序，而无需实际知晓交集内容。

基于排列的机制 本方法的核心在于利用排列信息作为两个关键阶段之间的桥梁，即ID安全匹配与特征对齐。在PEAFOWL中，参与方$P_i,i\in \left[N\right]$作为数据提供者无法获取排列信息，因此无法知晓交集内容。云服务器$\mathcal{S}$负责计算排列并协助各方在不访问原始数据的情况下对齐样本，其交互过程如图4所示。该机制的顶层逻辑如下：

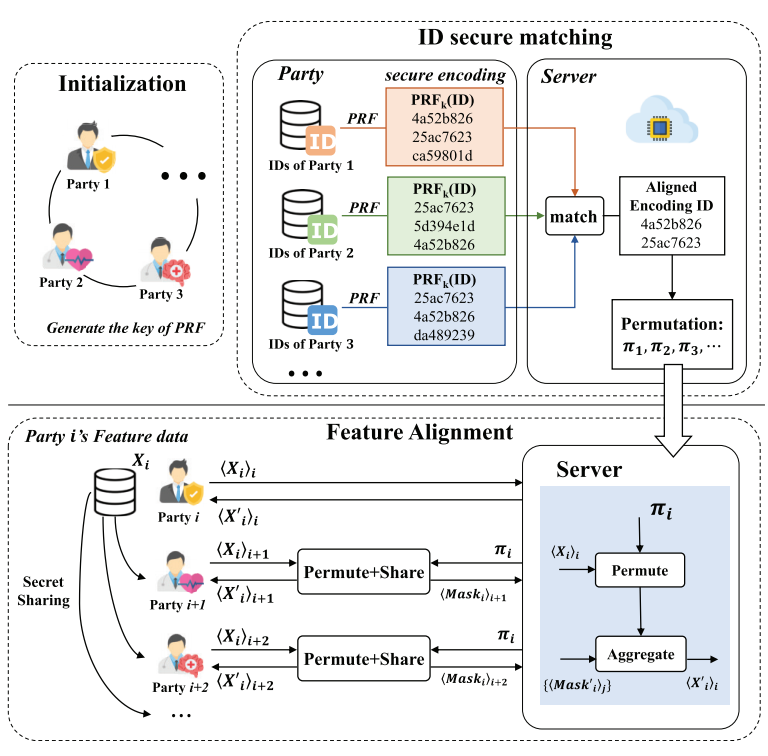
图4. PEAFOWL架构概览

1. ID安全匹配：每个数据提供者$P_i$对其唯一标识符${\mathbf{I}}_i$进行安全编码，将编码后的${\mathbf{EI}}_i$发送至$\mathcal{S}.\mathcal{S}$进行匹配，计算交集${\mathbf{I}}_A$及将原始集合映射到对应交集元素的排列${\pi }_i$，即${\mathbf{I}}_A={\pi }_i\left({\mathbf{I}}_i\right)$。

2. 特征对齐：每个$P_i$将其特征数据${\mathbf{X}}_i$安全共享给其他参与方$P_j\left(j\ne i\right)$，并将共享份额${⟨{\mathbf{X}}_i⟩}_i$提交至$\mathcal{S}$。服务器$\mathcal{S}$提供相应排列信息，协助各方$P_j\left(j\ne i\right)$对齐接收到的共享份额${⟨{\mathbf{X}}_i⟩}_j$并返回排列后的${⟨{\mathbf{X}}_i⟩}_i$。

本机制中，$P_i$始终无法获知其数据集对应的排列${\pi }_i$，服务器也无法访问原始数据集。通过排列机制，任何参与方都无法推断交集内容。虽然该机制会公开排列中的基数$n_A$以帮助服务器排除非交集数据，但相比直接的$mPSI+$共享方法，我们的方案为交集提供了更强的隐私保护。类似工作iPrivJoin同样采用排列信息，但其先确定交集再使用随机排列消除冗余样本，而我们的方法直接利用排列信息同步确定交集并消除冗余样本。

然而设计安全的特征对齐协议存在重大挑战。直观方案是由服务器分发ID安全匹配阶段获得的排列${\pi }_i,i\in \left[N\right]$给参与方$P_j,j\in \left[N\right]\setminus i$（原始数据提供者$P_i$除外），再由各方$P_j,j\in \left[N\right]\setminus i$计算排列后的共享份额${\pi }_i\left({⟨{\mathbf{X}}_i⟩}_j\right),i\in \left[N\right]\setminus j$。

遗憾的是，该方法仍存在若干待解决问题：首先，数据提供方知晓其原始份额${⟨{\mathbf{X}}_i⟩}_i$，可能通过服务器置换后的份额${\pi }_i\left({⟨{\mathbf{X}}_i⟩}_i\right)$与原始数据库位置关联，从而推断交集；其次，直接向其他参与方$P_j$传输置换序列${\pi }_i,i\in \left[N\right]\setminus j$存在泄密风险，接收方可能向数据提供方泄露置换规则；再者，单纯使用加法秘密共享传输特征数据${⟨{\mathbf{X}}_i⟩}_j$会导致较高通信开销，需引入PRGs（伪随机数生成器）降低负担，但可能影响对齐流程兼容性。

针对这些问题，我们开发了安全协议PEAFOWL及其密码学变体（详见第III节），通过安全管理共享与对齐流程，有效防范隐私泄露并控制开销。

B.PEAFOWL协议

如图5所示，我们详细构建了PEAFOWL协议。为简化描述，假定各方输入数据规模$n$相同，特征长度均为$m$，且所有ID在输入协议前已通过相同哈希函数统一映射为$\kappa$位唯一值。

图5. PEAFOWL协议说明。

1. 初始化阶段：通过数据混洗隐藏原始顺序。执行前，各方{Pi}i∈[N]{\left\{ {P}_{i}\right\} }_{i \in \left\lbrack N\right\rbrack }{Pi​}i∈[N]​协商生成${\mathcal{F}}_{prf}$的随机密钥$k_F$，并同步混洗各自数据集Di={Ii,Xi}{D}_{i} = \left\{ {{\mathbf{I}}_{i},{\mathbf{X}}_{i}}\right\}Di​={Ii​,Xi​}。该操作可防止服务器根据默认样本顺序等先验知识推断具体信息。

2. ID安全匹配：安全编码ID并提取排列组合。每个$P_i$在${\mathbf{I}}_i$上运用${\mathcal{F}}_{\text{prf }}$，生成对应的编码ID集${\mathbf{EI}}_i$，随后将其传输至$\mathcal{S}$。服务器通过匹配${\mathbf{EI}}_i$中的元素识别交集${\mathbf{EI}}_A$。接着对交集进行乱序处理，提取将原始数据集映射到该交集的排列组合。此步骤采用乱序技术确保交集元素随机排列，从而仅获得看似随机的排列结果，防止下一步骤中向用户泄露信息。

3. 特征对齐：分割、掩码与置换特征。参与方$P_i$将原始特征数据${\mathbf{X}}_i$分割为$N$份随机份额（统称为${⟨{\mathbf{X}}_i⟩}_j,j\in \left[N\right]$）。如前述，服务器需对原始份额进行掩码处理，防止数据提供者追踪置换后份额的来源。同时服务器必须在不暴露置换规则的情况下对各参与方收到的份额进行置换。可采用Permute+Share[27]方案，该方案提供强隐私保障（排列隐藏性与份额隐藏性），利用这些特性可实现：

对于${⟨{\mathbf{X}}_i⟩}_j\left(i,j\in \left[N\right],i\ne j,k\in \left[m\right]\right)$中的第$k$个维度：

• 输入：$\mathcal{S}$输入${\pi }_i$，接收方$P_j$向Permute+Share输入${⟨{\mathbf{X}}_i⟩}_j^k$

• 输出：$\mathcal{S}$与$P_j$分别获得${⟨{\pi }_i\left({\mathbf{X}}_i\right)⟩}_{{\mathcal{S}}_j}^k$和${⟨{\pi }_i\left({\mathbf{X}}_i\right)⟩}_{P_j}^k$，且无法获知对方输入

为提高效率，我们可以显著降低通信成本，方法是让参与方像许多多方计算框架那样使用种子。伪随机数生成器(PRG)将这些种子扩展为任意所需长度的随机份额或掩码。这意味着每个参与方只需传输单个种子而非整个份额。我们可在PEAFOWL中实施该策略，让每个参与方$P_i$与其他参与方$j\in \left[N\right]/i$共享种子${\mathbf{s}}_{ij}$，从而按如下方式计算共享向量：

$${⟨{\mathbf{X}}_i⟩}_i={\mathbf{X}}_i-\sum _{j\in \left[N\right]\setminus i}\mathcal{G}\left({\mathbf{s}}_{ij}\right),\text{\hspace{1em}(4)}$$

$${⟨{\mathbf{X}}_i⟩}_j=\mathcal{G}\left({\mathbf{s}}_{ij}\right),j\in \left[N\right]\setminus i.\text{\hspace{1em}(5)}$$

然而该技巧不适用于PEAFOWL，因为无法在确保伪随机数生成器输出总和与原始种子匹配的前提下，将共享种子$\mathbf{s}$转换为独立的掩码版本${\mathbf{s}}^{\prime }$。因此我们需要替代方案。短同态伪随机数生成器(SHPRG)提供了解决方案，能有效降低通信成本。如第三节所示，SHPRG引入了近似加法同态特性，确保对于任意$N-1$种子集合$\mathbf{s},{\mathbf{s}}^{\prime }\in {\mathbb{Z}}_q^{d^{N-1}}$，下列等式成立：

$$\sum _{j\in \left[N\right]\setminus i}\mathcal{G}\left({\mathbf{s}}_j\right)=\sum _{j\in \left[N\right]\setminus i}\mathcal{G}\left({\mathbf{s}}_j^{\prime }\right)+\sum _{j\in \left[N\right]\setminus i}\mathcal{G}\left({\mathbf{s}}_j-{\mathbf{s}}_j^{\prime }\right)+e,\text{\hspace{1em}(6)}$$

其中$e\in {\left[-N+1,N-1\right]}^m$。实际操作中，每个参与方$i$生成并发送SHPRG的对应种子${\mathbf{s}}_{ij}$给其他参与方$P_j$，同时将其秘密份额${⟨{\mathbf{X}}_i⟩}_i$发送至服务器$\mathcal{S}$。

随后如前所述，我们采用置换+共享方案。服务器调用${\mathcal{F}}_{ps}$并输入置换参数${\pi }_i$，而每个份额持有者$P_j$使用对应种子${\mathbf{s}}_{ij}$调用该方案。执行后，服务器获得置换后的共享结果${\mathbf{s}}_{ij}^{\prime }\leftarrow {⟨{\pi }_i\left({\mathbf{s}}_{ij}\right)⟩}_{\mathcal{S}}$，$P_j$则得到满足以下条件的${\mathbf{s}}^{\prime }{}_{ij}^{P_j}\leftarrow {⟨{\pi }_i\left({\mathbf{s}}_{ij}\right)⟩}_{P_j}$：

$${\mathbf{s}}^{\prime }{}_{ij}^{\mathcal{S}}+{\mathbf{s}}^{\prime }{}_{ij}^{P_j}={\pi }_i\left({\mathbf{s}}_{ij}\right).\text{\hspace{1em}(7)}$$

对于$i\in \left[N\right]$，服务器对秘密份额${⟨{\mathbf{X}}_i⟩}_i$进行置换，计算${⟨{\text{Mask}}_i⟩}_j\leftarrow \mathcal{G}\left({\mathbf{s}}^{\prime }{}_{ij}^{\mathcal{S}}\right)$并更新${⟨{\mathbf{X}}_i⟩}_i\leftarrow {\pi }_i\left({⟨{\mathbf{X}}_i⟩}_i\right)+$$\sum _{j\in \left[N\right]\setminus i}{⟨{\mathrm{Mask}}_i⟩}_j$，然后将结果返回给$P_i$。

最终，各方$j$根据种子${\mathbf{s}}^{\prime }{}_{ij}^{P_j}$生成$P_i$数据集秘密份额${⟨{\mathbf{X}}_i^{\prime }⟩}_j$，并通过拼接这些份额得到目标数据集（即${⟨{\mathbf{X}}_A⟩}_j\leftarrow \prod _{i\in \left[\mathbb{N}\right]}{⟨{\mathbf{X}}_i^{\prime }⟩}_j$）。其正确性可证明如下：对于第$j$个数据集的份额：

$$\sum _{j\in \left[N\right]}{⟨{\mathbf{X}}_i^{\prime }⟩}_j$$

$$={⟨{\mathbf{X}}_i^{\prime }⟩}_i+\sum _{j\in \left[N\right]\setminus i}\mathcal{G}\left({\mathbf{s}}_{ij}^{\prime }\right)$$

$$={\pi }_i\left({⟨{\mathbf{X}}_i⟩}_i\right)+\sum _{j\in \left[N\right]\setminus i}\mathcal{G}\left({⟨{\pi }_i\left({\mathbf{s}}_{ij}\right)⟩}_{\mathcal{S}}\right)+\sum _{j\in \left[N\right]\setminus i}\mathcal{G}\left({⟨{\pi }_i\left({\mathbf{s}}_{ij}\right)⟩}_{P_j}\right)$$

$$={\pi }_i\left({⟨{\mathbf{X}}_i⟩}_i\right)+\sum _{j\in \left[N\right]\setminus i}\mathcal{G}\left({⟨{\pi }_i\left({\mathbf{s}}_{ij}\right)⟩}_{\mathcal{S}}+{⟨{\pi }_i\left({\mathbf{s}}_{ij}\right)⟩}_{P_j}\right)+e$$

$$={\pi }_i\left({\mathbf{X}}_i-\sum _{j\in \left[N\right]\setminus i}\mathcal{G}\left({\mathbf{s}}_{ij}\right)\right)+\sum _{j\in \left[N\right]\setminus i}\mathcal{G}\left({\pi }_i\left({\mathbf{s}}_{ij}\right)\right)+e$$

$$={\pi }_i\left({\mathbf{X}}_i\right)+e,\text{\hspace{1em}(8)}$$

存在误差$e\in {\left[-N+1,N+1\right]}^m$。需注意引入误差的影响微乎其微。如$\S$第三节所述，特征数据的精度为$L=16$。参与方数量$N$（通常约10个）仅在特征数据最低有效位引入微小误差，这些误差不太可能显著影响模型训练。

C. 离线/在线PEAFOWL协议

在多方安全计算（MPC）中，即使会略微增加总运行时间，引入离线阶段也是常规做法。当前最高效的MPC框架均已包含用于生成随机数（例如Beaver三元组）的离线阶段。PEAFOWL同样基于Permute+Share的特殊结构，利用离线预计算降低通信成本。[27]提出通过份额转换（Share Translation）构建PEAFOWL中Permute+Share的方法如下：

给定$\mathcal{S}$个输入$\pi$和$P$个秘密输入$\mathbf{x}$，执行：

1. $\mathcal{S}$与$P$执行份额转换协议：$\mathcal{S}$持有输入$\pi$，获得输出$\Delta$；$P$获得$\mathbf{a},\mathbf{b}$

2. $P$将$\mathbf{x}-\mathbf{a}$发送至$\mathcal{S}$，并设置其最终份额为$\mathbf{b}$

3. $\mathcal{S}$将其份额设为$\pi \left(\mathbf{x}-\mathbf{a}\right)+\mathbf{\Delta }$

注意以下等式成立：

$$\pi \left(\mathbf{x}-\mathbf{a}\right)+\mathbf{\Delta }+\mathbf{b}=\pi \left(\mathbf{x}-\mathbf{a}\right)+\pi \left(\mathbf{a}\right)-\mathbf{b}+\mathbf{b}=\pi \left(\mathbf{x}\right).\text{\hspace{1em}(9)}$$

因此，$\mathcal{S}$和$P$确实获得了$\pi \left(\mathbf{x}\right)$的秘密份额，符合Permute+Share的理想输出。

此处需注意，份额转换的操作与机密输入$\mathbf{x}$无关，仅与置换$\pi$相关。这一特性使得我们可以将份额转换过程移至离线阶段。各方可预先与服务器计算获得$\mathbf{\Delta },\mathbf{a}$和$\mathbf{b}$，这种预计算将在线阶段简化为简单的加法与传输。

基于此思路，我们如下描述PEAFOWL的离线/在线变体（图6所示），重点说明其与基础版本的区别及原因：

图6. 离线/在线PEAFOWL协议描述

1. 离线阶段：如前所述，服务器与各方预先离线执行份额转换（Share Translation），采用随机置换${\pi }_i^{\prime }$。按基础协议执行时，服务器应获取针对参与方$i$数据集的置换${\pi }_i$。但在离线阶段，即使没有可用编码ID，服务器也需确定随机置换${\pi }_i^{\prime }$用于离线份额转换。各方利用份额转换预先离线生成$\mathbf{b}$（此为最终特征对齐的关键），可预估所需份额量$n_A^{\prime }$，或提前准备$50\%$，并独立创建共享种子及预计算伪随机数生成器输出，实现高效共享准备。

2. ID安全匹配：由于${\pi }_i^{\prime }$是从$\left[n\right]$到$\left[n\right]$的映射，存在一个置换${\pi }_i^{\prime \prime }$可将随机生成的${\pi }_i^{\prime }$转换为${\pi }_i$。为确保该预定置换在后续步骤中的正确性，服务器计算满足${\pi }_i={\pi }_i^{\prime }{\pi }_i^{\prime \prime }$的置换${\pi }_i^{\prime \prime }$并将其发送至$P_i$。随后$P_i$对其数据集${\pi }_i^{\prime \prime }\left(D_i\right)$进行重排，从而得到${\mathbf{I}}_A=\pi \left(D_i\right)={\pi }^{\prime }\left({\pi }^{\prime \prime }\left(D_i\right)\right)$，其中${\pi }_i^{\prime }$即为所需置换。由于预定置换${\pi }_i^{\prime }$具有保密性，该过程不会泄露任何敏感信息，实现了离线/在线协议。鉴于${\pi }_i^{\prime }$随机生成且交集被随机打乱，${\pi }_i^{\prime \prime }$与随机选择的置换不可区分，且不会泄露交集信息。

3. 特征对齐：与基础协议相同，服务器和各参与方通过完成剩余加法运算及传输来实现置换共享(Permute+Share)。

并行性讨论：本协议主要优势之一在于高度并行化。我们提供了离线/在线PEAFOWL各步骤的可视化说明，详见附图7。根据整体流程，参与方可视为具有双重角色：处理自身数据集的$P_i$角色和处理他人数据集的$P_j$角色。由于采用分布式架构，部分步骤可实现并行化。同一行显示的步骤可并行执行。

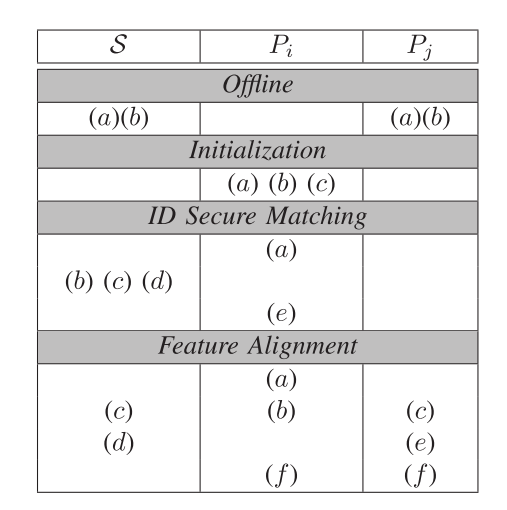
图7. 协议中详细步骤运行的示意图。

D. 复杂度分析

随后我们分析了PEAFOWL协议的计算与通信开销。由于变体方案成本近乎相同，我们将一并讨论二者。

参与方计算成本：基础协议中，各参与方计算成本为$\mathcal{O}\left(Nn\log n+Nnm\right)$，而离线/在线变体中分别为$\mathcal{O}\left(Nn\log n\right)$（离线阶段）和$\mathcal{O}\left(Nnm\right)$（在线阶段）。第二阶段：计算${\mathcal{F}}_{\text{prf }}$编码需要$\mathcal{O}\left(n\right)$次运算。第三阶段：生成共享种子耗费$\mathcal{O}\left(Nn\right)$次运算，计算上传至云服务器的份额需要$\mathcal{O}\left(nm\right)$次运算。参与方$P_i$调用${\mathcal{F}}_{ps}$或${\mathcal{F}}_{st}$需$\mathcal{O}\left(Nn\log n\right)$次运算。为$N-1$个参与方生成规模为$n_A=\beta n$的交集秘密$m$份额需$\mathcal{O}\left(Nnm\right)$次运算。

参与方通信成本：基础协议中，单方通信成本为$\mathcal{O}\left(Nn\log n+nm\right)$，离线/在线变体中分别为$\mathcal{O}\left(Nn\log n\right)$（离线阶段）和$\mathcal{O}\left(nm\right)$（在线阶段）。第二阶段：提交${\mathcal{F}}_{\text{prf }}$编码消耗$\mathcal{O}\left(n\right)$单位带宽。第三阶段：向其他参与方传输种子需$\mathcal{O}\left(Nn\right)$个${\mathbb{Z}}_p$元素，向云服务器提交份额需$\mathcal{O}\left(nm\right)$个${\mathbb{Z}}_{2^{\ell }}$元素。与服务器交互调用${\mathcal{F}}_{ps}$或${\mathcal{F}}_{st}$消耗$\mathcal{O}\left(Nn\log n\right)$单位带宽及种子数据，接收份额需获取$\mathcal{O}\left(nm\right)$个${\mathbb{Z}}_{2^{\ell }}$元素。

服务器计算成本：基础协议中，服务器计算成本为$\mathcal{O}\left(N^{2}n\log n+Nnm\right)$，离线/在线变体中分别为$\mathcal{O}\left(N^{2}n\log n\right)$（离线阶段）和$\mathcal{O}\left(Nnm\right)$（在线阶段）。第二阶段：使用哈希表计算交集需$\mathcal{O}\left(Nn\right)$次运算，乱序操作同样消耗$\mathcal{O}\left(Nn\right)$次运算。第三阶段：服务器调用${\mathcal{F}}_{ps}$或${\mathcal{F}}_{st}\mathcal{O}\left(N^2\right)$次操作，耗费$\mathcal{O}\left(N^{2}n\log n\right)$次运算。计算交集共享需$\mathcal{O}\left(Nnm\right)$次运算。

服务器的通信开销：在基础协议中，服务器的通信成本为$\mathcal{O}\left(N^{2}n\log n+Nnm\right)$，而离线/在线变体方案中离线阶段为$\mathcal{O}\left(N^{2}n\log n\right)$、在线阶段为$\mathcal{O}\left(Nnm\right)$。第二阶段：接收编码ID消耗$\mathcal{O}\left(Nn\right)$。第三阶段：从$N$个参与方接收$\mathcal{O}\left(nm\right)$份共享需消耗${\mathbb{Z}}_{2^{\ell }}$中的$\mathcal{O}\left(Nnm\right)$个元素。调用${\mathcal{F}}_{ps}$或${\mathcal{F}}_{st}\mathcal{O}\left(N^2\right)$次操作消耗$\mathcal{O}\left(N^{2}n\log n\right)$，发送共享需消耗${\mathbb{Z}}_{2^{\ell }}$中的$\mathcal{O}\left(Nnm\right)$个元素。

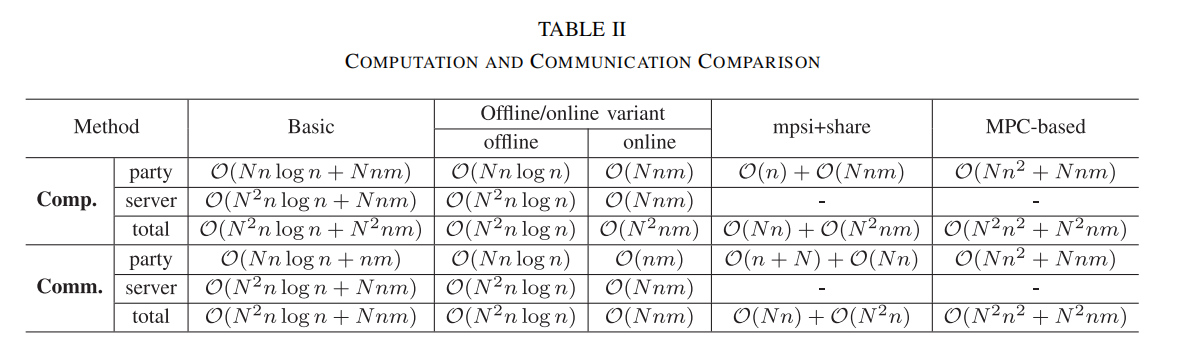
表II展示了我们提出的解决方案及其变体的计算与通信复杂度，并与$\S$ IV-A节描述的原始协议$mPSI+$共享和基于MPC的方法进行对比。MPSI+Share方案的复杂度明显低于我们的方法，因为它仅共享公共交集种子，但这是以牺牲安全性换取效率。不过，我们的离线优化成功将在线成本降至线性级别。$\S$ VI节详述的实验表明，尽管复杂度增加，但与训练过程中的巨大开销相比，仍完全在可容忍范围内。此外，PEAFOWL优于基于MPC的方法，特别是考虑到后者使用了大量昂贵的比较协议。

五、安全性证明

本节将阐述PEAFOWL的安全保证，并通过基于模拟的证据正式证明半诚实模型下的隐私性。参与方包括外包云服务器$\mathcal{S}$和拥有本地数据集Di={Ii,Xi}{\mathbf{D}}_{i} = \left\{ {{\mathbf{I}}_{i},{\mathbf{X}}_{i}}\right\}Di​={Ii​,Xi​}的$N$个参与方$P_i$。底层密码学构件以安全参数$\lambda$实例化。

A. 基于模拟的安全性证明

我们采用半诚实视角，即参与者遵守协议但好奇对方原始数据。在现实世界与理想世界的模拟证明下，任一方计算所得均可仅通过协议期间接收的消息进行模拟，这意味着各方从协议执行中获取的信息不超出所接收消息的推导范围。为形式化安全证明，需引入以下符号：

• 设$f\left(x_1,x_2,\dots ,x_k\right),i\in \left[k\right]$表示具有$k$个变量的函数，其中xi∈{0,1}ω,i∈[k]{x}_{i} \in \{ 0,1{\} }^{\omega },i \in \left\lbrack k\right\rbrackxi​∈{0,1}ω,i∈[k]可为任意数学对象（如整数、向量或泛函）的编码。$\omega$代表问题规模。

在执行$\Pi$过程中，第$i$方的真实视图记为$\mathcal{VI}\mathcal{E}{\mathcal{W}}_i^{\Pi }\left(x_1,\dots ,x_k,\lambda \right)$，可展开为$\left(x_i,{\mathbf{r}}^i,{\mathbf{m}}^i\right)$。其中$x_i$表示第$i$方的输入，${\mathbf{r}}^i$为其内部随机比特，${\mathbf{m}}^i$则是第$i$方在执行$\Pi$期间接收或衍生的消息。需注意${\mathbf{m}}^i$包含所有接收的中间消息、从中间消息衍生的信息以及第$i$方的输出结果。

定义1（半诚实模型下的安全性）：设$f\left(x_1,\dots ,x_k\right)$为函数。若存在针对第$i$方的$k$个概率多项式时间（PPT）算法$\mathcal{S}\mathcal{I}{\mathcal{M}}_i$，使得当所有参与方被视为半诚实敌手时，协议$\Pi$能计算$f$且对第i方存在$v_i$信息泄露，则称该$k$方协议满足条件。

$${\left\{\left(\mathcal{S}\mathcal{I}{\mathcal{M}}_i\left(1^{\lambda },x_i,v_1\left(x_1,\dots ,x_k\right)\right)\right)\right\}}_{x_1,\dots ,x_k,\lambda }$$

$$\stackrel{c}{\equiv }\left\{\left(\mathcal{VI}\mathcal{E}{\mathcal{W}}_i^{\Pi }\left(x_1,\dots ,x_k,\lambda \right)\right)\right\},\text{\hspace{1em}(10)}$$

其中x1,…,xk∈{0,1}∗{x}_{1},\ldots ,{x}_{k} \in \{ 0,1{\} }^{ * }x1​,…,xk​∈{0,1}∗和$\lambda$为安全参数，$\equiv$表示计算不可区分性。

B. 安全性证明

本节我们将给出PEAFOWL及其变体的安全性证明。

定理1：PEAFOWL协议（见第IV-B节）在半诚实模型下是安全的，仅会向$\mathcal{S}$泄露对齐数据集的基数$n_A$。

证明：我们首先简要讨论PEAFOWL的安全性与信息泄露情况。在初始化阶段，ID集合在${\mathcal{F}}_{\text{prf }}$机制下被移交至$\mathcal{S}$，因此$\mathcal{S}$仅能通过比较加密元素获知基数$n_A$，而无法获取ID的具体信息[42]。这种程度的信息披露是合理的，因为我们保护了ID交集细节并隐藏了私有特征数据。在ID安全匹配阶段，置换操作使多方共享数据对齐。根据Permute+Share或Share Translation安全机制，该步骤不会导致关于置换和份额的任何信息泄露。最终，各方收到的是经过置换的掩码份额，这些份额与其发送给服务器的原始份额相互独立，因此无法获取关于自身数据份额的额外信息。

接下来，我们运用前文所述的预备技术深入分析PEAFOWL的安全等级。根据第$\S$章第三节描述的半诚实安全设定，我们考虑两种情况：(i)存在最多$N-1$个半诚实合谋的参与方子集，而服务器保持诚实；(ii)服务器本身是半诚实敌手。

腐败参与方：具体而言，对于任何具有$\left|\mathcal{C}\right|<N$的敌手子集$\mathcal{C}$，诚实方$\mathcal{P}/\mathcal{C}$的最终值应呈现均匀随机分布。为证明这点，我们采用标准混合论证法。通过定义混合分布序列${\mathbf{hyb}}_0,{\mathbf{hyb}}_1,\dots$，并逐步修改$\mathcal{VI}\mathcal{E}\mathcal{W}$来构建模拟器$\mathcal{S}\mathcal{I}\mathcal{M}$。换言之，若任意两个连续混合分布在计算上不可区分，则模拟器$\mathcal{S}\mathcal{I}\mathcal{M}$的分布与实际执行$\mathcal{VI}\mathcal{E}\mathcal{W}$亦相同。每个混合分布的正式定义如下，对应图5中的步骤。

• hyb${}_0^{\mathcal{C}}$：$\mathcal{S}\mathcal{I}\mathcal{M}$的$\mathcal{C}$联合视图分布与$\mathcal{VI}\mathcal{E}\mathcal{N}$相同。

• hyb${}_1^{\mathcal{C}}$：在步骤1-(a)中，我们调用${\mathcal{F}}_{\text{coin }}$的模拟器来模拟PRF密钥协商中的视图。

• hyb${}_2^{\mathcal{C}}$：在步骤2-(b)中，我们从$P_j\in \mathcal{C}$的输出获取对齐数据集大小$n_A$后进行广播。

• hyb${}_3^{\mathcal{C}}$：在步骤3-(a)中，对于每个参与方$P_i\in \mathcal{P}/\mathcal{C}$，将发送给敌手客户端$P_j$的模拟诚实方$P_i$种子${\mathbf{s}}_i^j$替换为对应域中随机选取的元素。由于协议中种子本就是随机选取的，该混合分布与先前分布一致。

• ${\mathbf{hyb}}_4^{\mathcal{C}}$：在步骤3-©中，对于每个参与方$P_j\in \mathcal{C}$，我们将Permute+Share中服务器的输入$\pi$替换为随机排列${\pi }_r\stackrel{\mathrm{S}}{\leftarrow }{\Pi }_{\left[n\right]}$。根据$\S$第三节讨论的Permute+Share的排列隐藏性[27]特性，${\mathbf{hyb}}_3^{\mathcal{C}}$与${\mathbf{hyb}}_4^{\mathcal{C}}$呈现计算不可区分性。

• 混合实验${}_5^{\mathcal{C}}$：在步骤3-(d)中，对于每个参与方$P_j\in \mathcal{C}$，不再使用SHPRG$\mathcal{G}$计算掩码份额${⟨{\mathbf{X}}_i^{\prime }⟩}_j$，而是将每个$P_i$的份额替换为等长随机数。前一混合实验中种子均匀选择且敌手种子设为0，使得SHPRG输出与种子无关。由于$\mathcal{C}$中的敌手未获取全部附加份额或$P_i\in \mathcal{P}/\mathcal{C}$的种子，其联合视图最多包含$\left|\mathcal{C}\right|\le N-1$个${\mathbf{X}}_i$的份额。Shamir秘密共享与SHPRG的安全特性确保敌手无法获知掩码份额信息，保持本混合实验与前一实验的分布一致性。

通过构建如前文混合实验所述的PPT模拟器$\mathcal{S}\mathcal{I}\mathcal{M}$，半诚实敌手的联合视图与实际执行$\mathcal{VI}\mathcal{E}\mathcal{W}$在计算上不可区分。

腐化服务器场景：令$\mathcal{S}$作为敌手并量化信息泄漏。类似地，我们采用如下标准混合论证：

• 混合实验${}_0^{\mathcal{S}}$：$\mathcal{S}\mathcal{I}\mathcal{M}$的$\mathcal{S}$联合视图分布与$\mathcal{VI}\mathcal{E}\mathcal{W}$相同。

• 混合实验${}_1^{\mathcal{S}}$：在步骤2-(a)中，假设$\mathcal{S}\mathcal{I}{\mathcal{M}}_{\mathcal{S}}$已掌握$n_A$作为先验知识。对于每个参与方$P_i\in \mathcal{P}$，将${\mathbf{EI}}_i$替换为对应域中随机选取的${\mathbf{r}}_i$个元素（含$n_A$个相等元素）。已知$k_F$时，${\mathcal{F}}_{\text{prf }}$输出与随机字符串不可区分，因此本实验分布与前一实验相同。

• 混合实验${}_2^{\mathcal{S}}$：在步骤3-(b)中，对于每个参与方$P_i\in \mathcal{P}$，不再使用SHPRG$\mathcal{G}$计算${⟨{\mathbf{X}}_i^{\prime }⟩}_i$，而是将每个$P_i$的份额替换为等长随机数。与${\mathbf{hyb}}_5^{\mathcal{C}}$类似，该替换基于Shamir秘密共享方案和SHPRG的安全特性，使得分布与前一混合实验保持一致。

• 混合实验${}_3^{\mathcal{S}}$：在步骤3-©中，对于每个参与方$P_i\in \mathcal{P}$，我们将Permute+Share中各方输入的种子替换为适当长度的随机选取数值。根据$\S$第三节所述的Permute+Share的分享隐藏特性，${\mathbf{hyb}}_2^{\mathcal{S}}$与${\mathbf{hyb}}_0^{\mathcal{S}}$在计算上不可区分。

因此，模拟视图与现实世界视图在计算上是不可区分的。综上所述，该协议在半诚实模型下安全运行，仅向$\mathcal{S}$透露对齐数据集的大小信息。

此外，离线/在线PEAFOWL的证明与上述过程类似。我们得出：

定理2：PEAFOWL的离线/在线变体（见第四-C节）在半诚实模型中具有安全性，仅向$\mathcal{S}$泄露对齐数据集的基数$n_A$。

证明：类似地，我们分两种情况给出证明。

腐败参与方：给定敌手集合$\mathcal{C}$，我们采用如下标准混合论证：

• 混合实验${}_0^{\mathcal{C}}$：$\mathcal{S}\mathcal{I}\mathcal{M}$的$\mathcal{C}$联合视图分布与$\mathcal{VI}\mathcal{E}\mathcal{N}$完全一致。

• ${\mathbf{hyb}}_1^{\mathcal{C}}$：在步骤0-(a)中，对于每个参与方$P_j\in \mathcal{C}$，我们将Share Translation中服务器的输入${\pi }^{\prime }$替换为随机排列。根据$\S$第三节所述的Share Translation排列隐藏属性，${\mathbf{hyb}}_0^{\mathcal{C}}$与${\mathbf{hyb}}_1^{\mathcal{C}}$不可区分。

• ${\mathbf{hyb}}_2^{\mathcal{C}}\&{\mathbf{hyb}}_3^{\mathcal{C}}$：与定理1中的${\mathbf{hyb}}_1^{\mathcal{C}}$和${\mathbf{hyb}}_2^{\mathcal{C}}$相同。

• ${\mathbf{hyb}}_4^{\mathcal{C}}$：在步骤2-(d)中，对于每个参与方$P_j\in \mathcal{C}$，我们随机采样排列${\pi }_r\stackrel{\mathrm{S}}{\leftarrow }{\Pi }_{\left[n\right]}$替代${\pi }^{\prime \prime }$。由于$P_j$不知晓${\pi }^{\prime }$，${\pi }^{\prime \prime }$与随机选取的排列不可区分，这使得混合实验${}_3^{\mathcal{C}}$与${}_4^{\mathcal{C}}$不可区分。

• 混合实验${}_5^{\mathcal{C}}\&{\mathbf{hyb}}_6^{\mathcal{C}}$：与定理1中的${\mathbf{hyb}}_4^{\mathcal{C}}$和${\mathbf{hyb}}_5^{\mathcal{C}}$相同。

腐败服务器：设$\mathcal{S}$为敌手，采用如下标准混合论证：

• 混合实验${}_0^{\mathcal{S}}$：本实验中，$\mathcal{S}\mathcal{I}\mathcal{M}$的$\mathcal{C}$联合视图分布与$\mathcal{VI}\mathcal{E}\mathcal{N}$完全一致。

• 混合实验${}_1^{\mathcal{S}}$：在步骤0-(a)中，对于每个参与方$P_i\in \mathcal{P}$，我们模拟各方调用共享转换(Share Translation)的过程。

• 混合实验${}_2^{\mathcal{C}}\&{\mathbf{hyb}}_3^{\mathcal{C}}$：与定理1中的${\mathbf{hyb}}_1^{\mathcal{C}}$和${\mathbf{hyb}}_2^{\mathcal{C}}$相同。

• 混合实验${}_4^{\mathcal{S}}$：在步骤3-©中，为每个参与方$P_i\in \mathcal{P}$将其输入的种子替换为随机选取的数字。由于$\mathcal{S}$不知晓$\mathbf{a}$，计算所得的种子与随机数不可区分。因此${\mathbf{hyb}}_3^{\mathcal{S}}$与${\mathbf{hyb}}_4^{\mathcal{S}}$具有不可区分性。

至此，离线/在线变体的分析已完成。

六、评估与实验

本节将评估PEAFOWL系统的效能与效率，并展示实验结果。实现代码已开源${}^1$。

A. 实验设置

1. 环境：我们在配备AMD EPYC罗马处理器和64GB内存的ECS服务器上部署PEAFOWL，所有实验使用32核运行。为模拟真实场景，对网络环境施加人工限制：重点关注$10\mathrm{Gbps}$带宽的局域网环境与100Mbps带宽的广域网环境。若无特别说明，默认网络设置为$10\mathrm{Gbps}$带宽。

2. 实现：主方案采用Python基于libOTe${}^2$等标准库实现。PEAFOWL中的置换共享(Permute+Share)与共享转换(Share Translation)功能基于C++代码${}^3$实现。密码学原语采用128位AES密钥的伪随机函数，并引用[43]使用$d=8,p=2^{64},q=2^{128}$构建的基于LWR的SHPRG生成随机字符串。

3. 基准测试：实验主要采用$\S$ IV-A所述的$mPSI+$共享方案及基于通用MPC的方案作为基准。其中mPSI采用文献[23]方案并结合秘密共享技术，详情可参阅${}^4$。为比较具备交集隐私性的多方方案，我们采用基于MPC[6]构建的方案。

4. 优化：在实现中通过并行化优化提升置换共享、共享转换步骤的效率，并采用PRG生成秘密份额。

B. PEAFOWL评估

实验中各方持有样本ID与原始图像数据特征，其中一方还持有标签。该设置常见于跨机构隐私保护机器学习(PPML)[10][13]。交集数据集中的数据均随机选取，默认交集率为$50\%$。

1. PEAFOWL效率验证：我们在模拟程序生成的线性支持向量机(SVM)数据集上验证PEAFOWL协议效率，对比基准测试报告了不同参与方数量、样本数量和特征维度在不同网络带宽下的预估运行时间。同时展示了协议中各实体间通信开销的变化情况。图8至10呈现实验结果：图8展示固定样本数${10}^4$和固定特征维度${10}^4$时，通信开销随参与方数量的变化；图9展示固定参与方数5和固定特征维度${10}^4$时，开销随样本数量的变化；图10展示固定参与方数5和固定样本量${10}^4$时，开销随特征维度的变化。所有曲线通过10个插值点生成。我们采用PEAFOWL输出进行模型训练，使用前沿多方计算框架CrypTen实现隐私保护机器学习(PPML)训练，该框架利用服务器$\mathcal{S}$作为第三方避免昂贵的实时随机数生成。

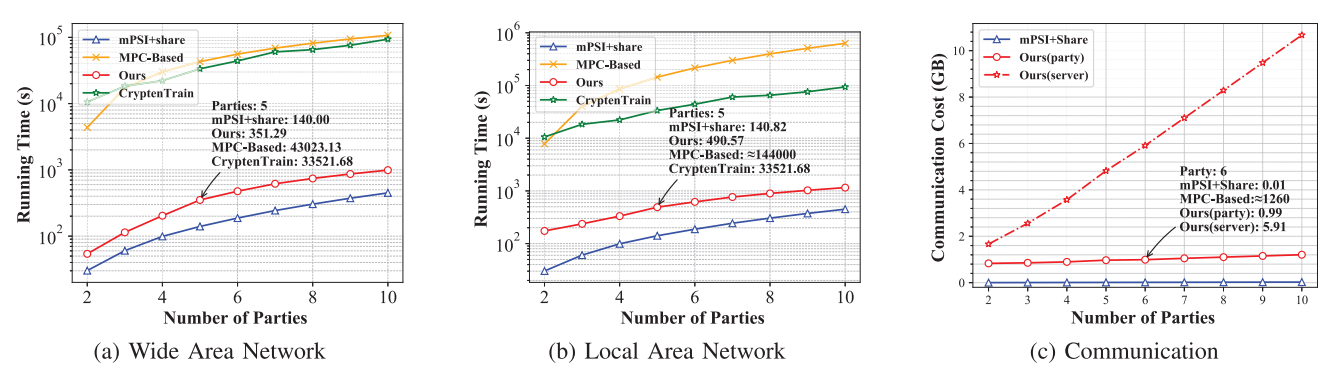
图8. 不同参与方数量下的运行时间与通信开销对比

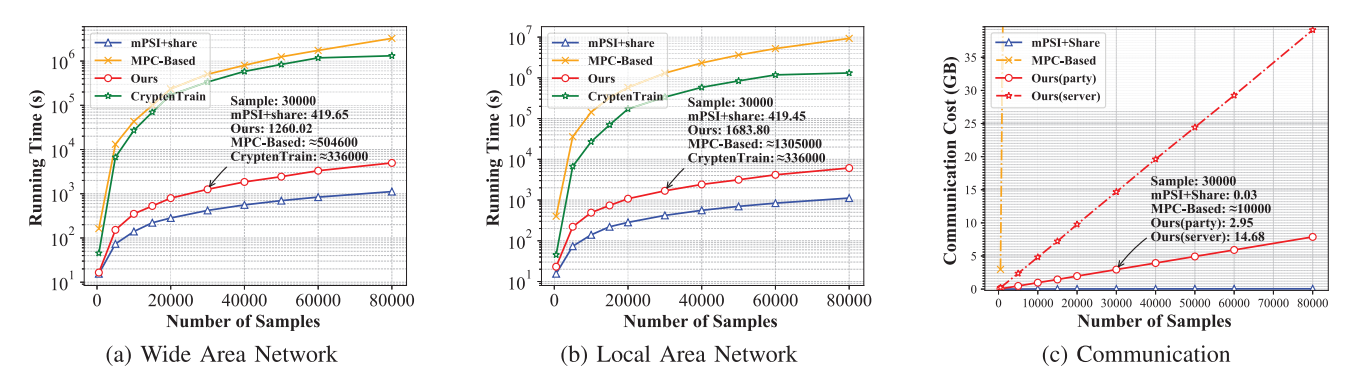
图9. 不同样本数量下的运行时间与通信开销对比

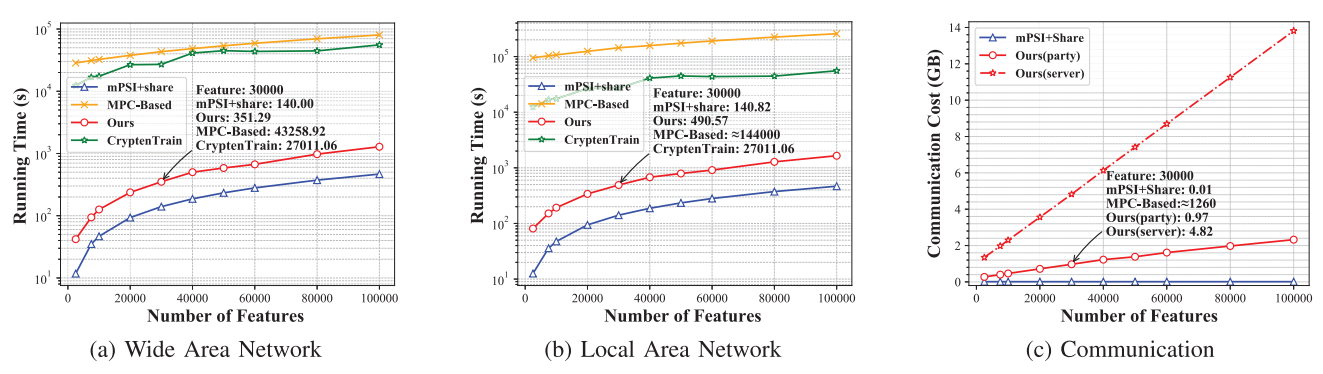
图10. 不同特征维度下的运行时间与通信开销对比

实验表明，服务器的时间开销和通信开销随参与方数量、样本量和特征维度近似线性增长，这是因为特征对齐阶段涉及特征数据的线性计算主导了整体开销。这也凸显PEAFOWL避免不必要特征数据计算的效率优势。客户端通信开销随样本量和特征维度线性增长，不受参与方数量影响，证明协议具备良好的多方扩展性。基准MPC方案虽能实现相同的交集隐私保护功能，但训练过程产生高昂计算通信开销，难以应对长特征场景。MPSI+share方案通过传输种子提升效率，但牺牲了交集隐私性。我们的方案通过选择性披露非关键置换信息，在保护交集隐私的同时实现更高效率，仅引入$\mathcal{O}\left(Nnm\right)$量级的共享通信开销。鉴于最新两方方案[20]同样在$\mathcal{O}\left(nm\right)$条件下运行且$N$固定为2，该开销可以接受。PPML主要成本在于模型训练，我们的方案未增加额外训练开销，总运行成本约占整体PPML成本的$1\%$，因此PEAFOWL在保障隐私性的同时保持了PPML效率。

2. 离线/在线PEAFOWL效率：图11展示了基本协议与离线/在线变体的运行时及通信开销对比，离线阶段参数设为$n_A^{\prime }=0.3n$。除可变参数外，其余固定参数与$\S$ VI-B1节设置相同。结果表明离线协议在保持总开销基本不变的前提下，有效降低在线阶段开销。运行时方面，离线协议使在线阶段开销在不同条件下降低约$50\%$，这是通过将置换操作和部分伪随机数生成器(PRG)计算移至离线预计算实现的。通信开销方面，PRG计算不涉及通信，仅置换操作产生开销，因此离线阶段通信开销不受特征变化影响，但与特征长度相关的PRG预计算仍能减少整体运行时间。随着参与方数量和样本规模增大，离线计算优势更加显著，有效避免了基础方案中在线通信开销的增长。

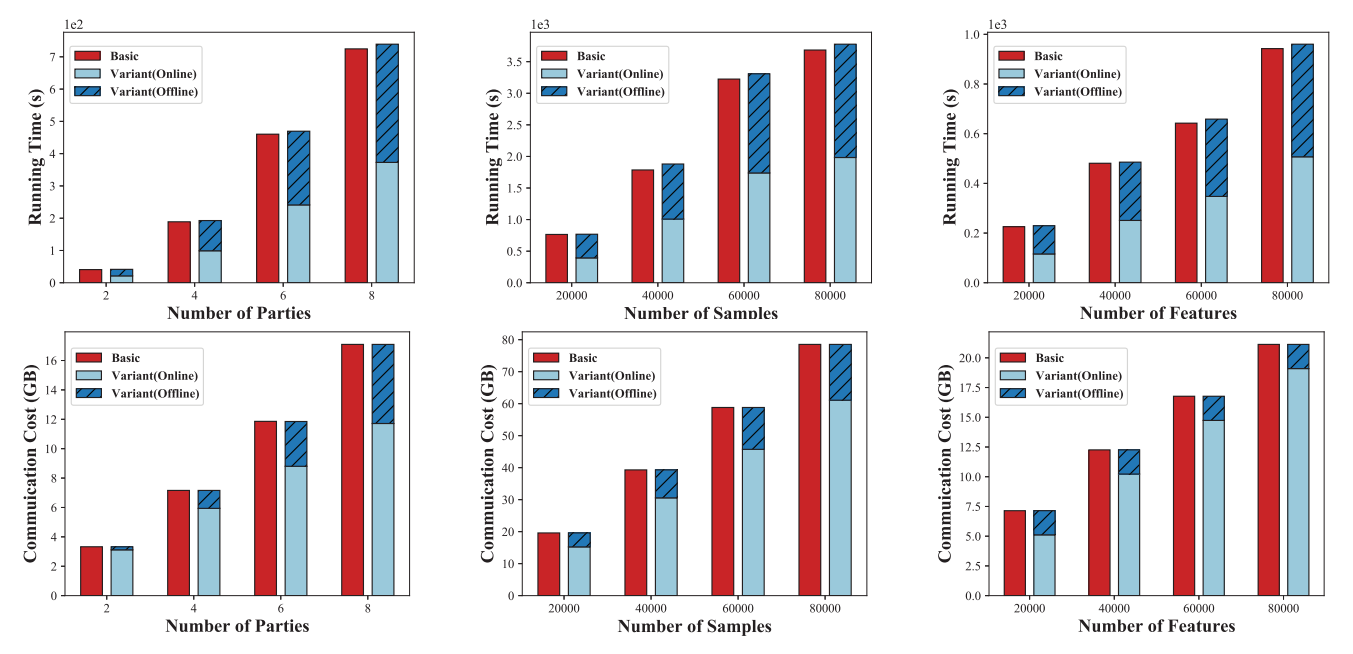
图11. 基础协议与离线/在线变体的运行时间及通信开销对比

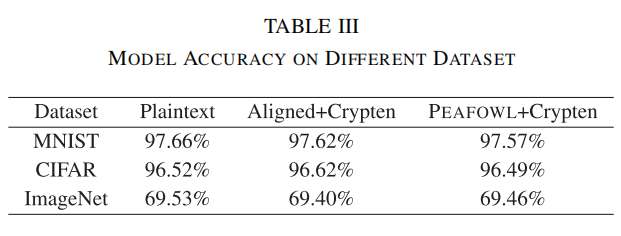
3. 训练准确性：在我们提出的协议中，使用SHPRG会引入微小的比特错误，这些错误可能影响模型精度。为评估对模型训练的影响，我们采用Crypten模型在三种数据类型（明文数据、对齐数据及PEAFOWL输出数据）上进行了实验，实验架构与超参数遵循文献[10]的设置。结果汇总于表III。此外，我们在MNIST、${}^5$CIFAR、${}^6$和ImageNet${}^7$三个数据集上评估了PEAFOWL。研究发现，基于PEAFOWL处理数据训练的Crypten模型准确率与明文数据及MPSI+数据基线几乎一致，表明误差影响可忽略不计。

七、结论

本文提出了一种创新的多方隐私保护机器学习协议PEAFOWL及其离线/在线变体。该协议填补了多方场景下的关键空白，在确保数据交集保密性的同时减少了不必要的数据开销。PEAFOWL不仅恪守严格的隐私标准，还通过密码学技术提升了效率，兼具可扩展性与广泛适用性。大量实验验证了其实用性与高效性，为多方PPML领域贡献了具有隐私保护能力的实体对齐新方案，有望推动该领域的进一步发展。

未来研究方向包括增强多方PPML的安全性、效率与适应性：开发能抵御恶意威胁且保护交集规模隐私的协议；优化协议以减少对特征数据的依赖；设计应对参与方退出的容错策略；实现无需第三方介入的自主运行系统。这些改进旨在强化现有框架，开拓多方PPML新方法，构建更安全、高效、自主的PPML生态。

这篇论文有很多没有接触过的内容，属实是看不懂，送给有需要的人~