NSA稀疏注意力深度解析：DeepSeek如何将Transformer复杂度从O(N²)降至线性，实现9倍训练加速

当前人工智能模型在处理长序列任务时面临着根本性的计算瓶颈。无论是分析完整的法律文档、处理大型代码仓库，还是进行长篇对话，现有模型都受到Transformer架构中注意力机制的限制——其计算复杂度随序列长度呈二次增长（

O(N²)

），导致计算和内存需求超出可承受范围。

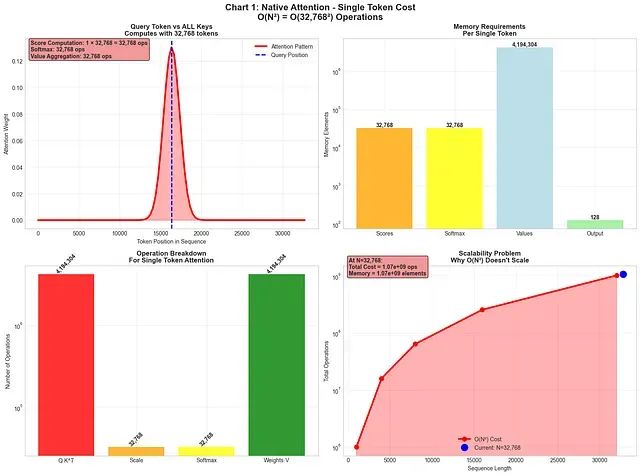
简单的O(N²)注意力机制，为简化起见未包含维度大小的计算成本；实际上Q.K^T和权重V需要与维度d相乘

**原生稀疏注意力（Native Sparse Attention，NSA）**是DeepSeek-AI团队开发的框架，专门针对这一挑战设计。NSA不仅是现有技术的渐进式改进，更代表了一种范式转变。该方法将直观的算法设计与深度硬件优化相结合，在保持模型性能的同时实现了显著的效率提升，并获得了ACL 2025年度奖项。

本文将深入分析NSA的架构设计，通过详细的示例、可视化展示和数学推导，构建对其工作机制的全面理解，从高层策略到底层硬件实现均有涉及。

本文分析场景的技术参数：

序列长度（N）设定为32,768个令牌，相当于一本短篇小说的长度。NSA的核心参数根据原始论文设置：滑动窗口大小

w=512

，压缩块大小

l=32

，压缩步长

d=16

，选择块大小

l'=64

，选择块数量

n=16

。

核心设计理念：模拟人类阅读认知模式

NSA的核心设计哲学源于对人类阅读行为的深入观察。人类在处理长文档时并非对每个词语给予相等的注意力，而是采用分层的认知策略。这种策略可以概括为三个并行的注意力机制：专注于当前句子的本地上下文处理、回顾前文章节的全局摘要理解，以及对关键段落和重要信息的选择性关注。

NSA将这种认知模式转化为三个计算分支的架构设计：

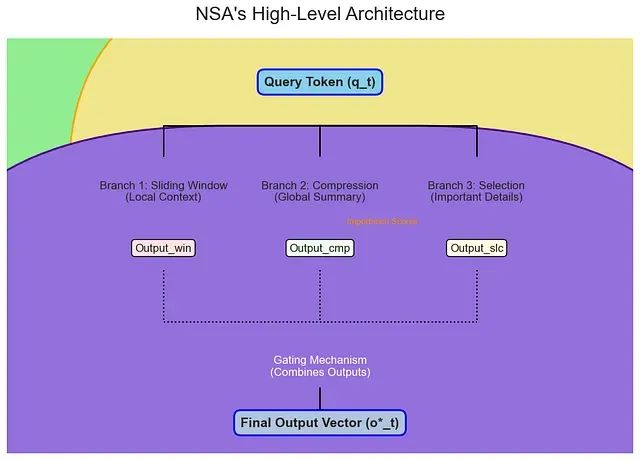
滑动窗口分支负责本地关注，令牌压缩分支提供全局摘要，令牌选择分支实现关键信息扫描。这三个分支的输出通过门控机制智能融合，形成完整的语义理解。

在深入技术细节之前，有必要分析NSA相对于现有稀疏注意力方法的核心优势。

首先是全阶段加速能力。许多现有方法存在"阶段限制"问题，仅能优化特定阶段，如H2O主要优化自回归解码，infLLM专注于预填充阶段。这种局部优化在多阶段工作负载中会产生瓶颈效应。NSA设计为全阶段优化，在训练、预填充和解码三个关键阶段均能提供显著的性能提升。

其次是端到端可训练性。稀疏注意力面临的主要挑战之一是训练过程中的梯度传播问题。使用非可微操作（如ClusterKV中的聚类算法）或仅在训练后应用稀疏性的方法往往导致性能退化。NSA采用原生可训练设计，使模型能够从训练初期就学习最优的稀疏模式，相比替代方案实现了更好的性能表现和更低的训练损失。

第三是硬件友好的设计原则。一些查询感知方法如Quest虽然能够减少计算量，但仍需要分散的内存访问模式，这与现代分组查询注意力（Grouped-Query Attention，GQA）的高效设计产生冲突。NSA的块级选择策略和以组为中心的内核设计明确考虑了硬件特性，确保理论性能提升能够转化为实际的执行速度优势。

第一部分：滑动窗口注意力机制

设计目标： 滑动窗口分支旨在完美保留最近本地上下文中的细粒度信息，确保模型对当前位置附近的语义关系具有高精度的理解能力。

实现机制： 该分支采用最直接的实现方式，将注意力计算限制在最近的

w=512

个键值对范围内，并在此局部窗口上执行标准的注意力计算。通过为本地模式提供专用的计算路径，NSA有效防止了这些高频本地模式对其他分支学习复杂长程依赖关系的干扰。

数学表达： 计算过程遵循标准注意力公式，但仅应用于本地窗口范围：

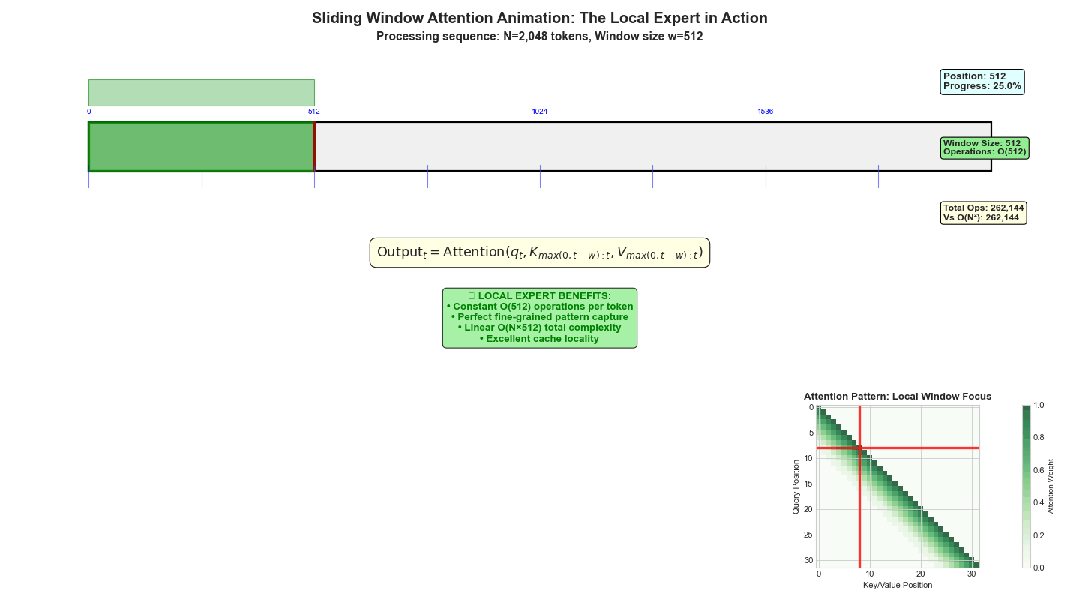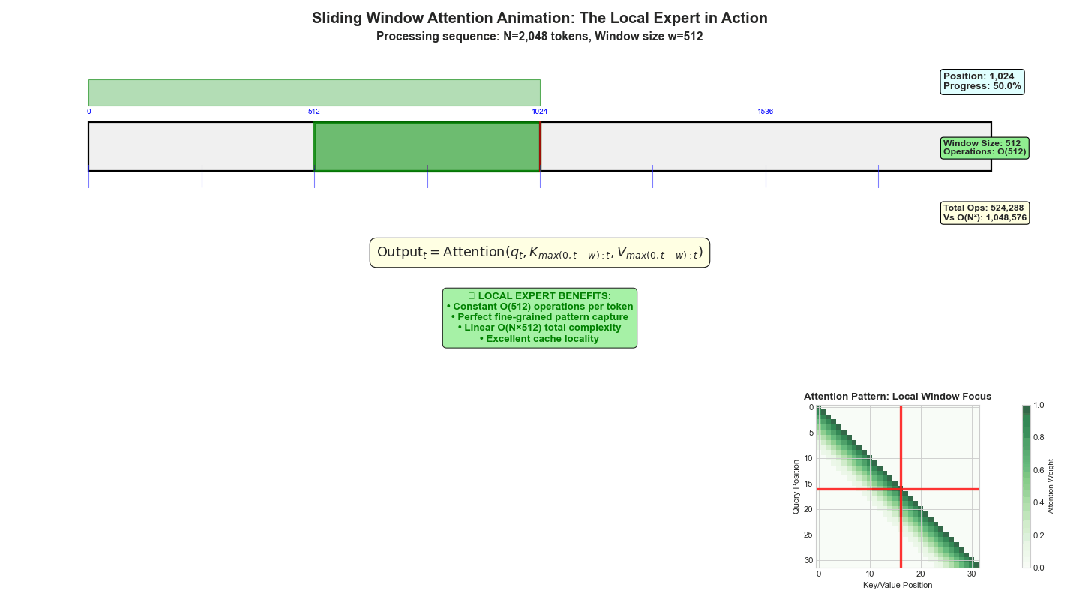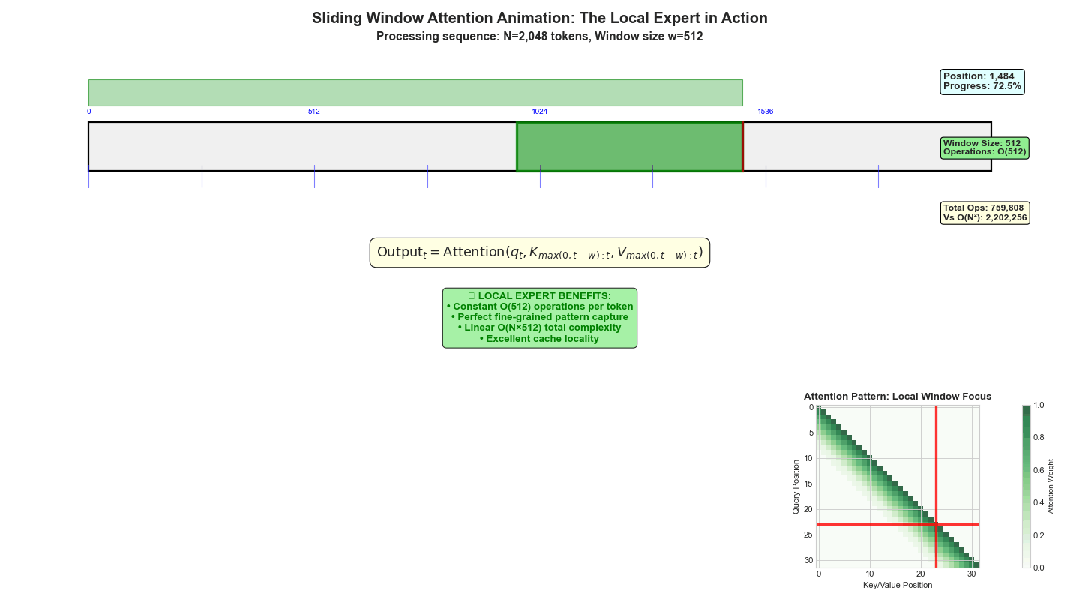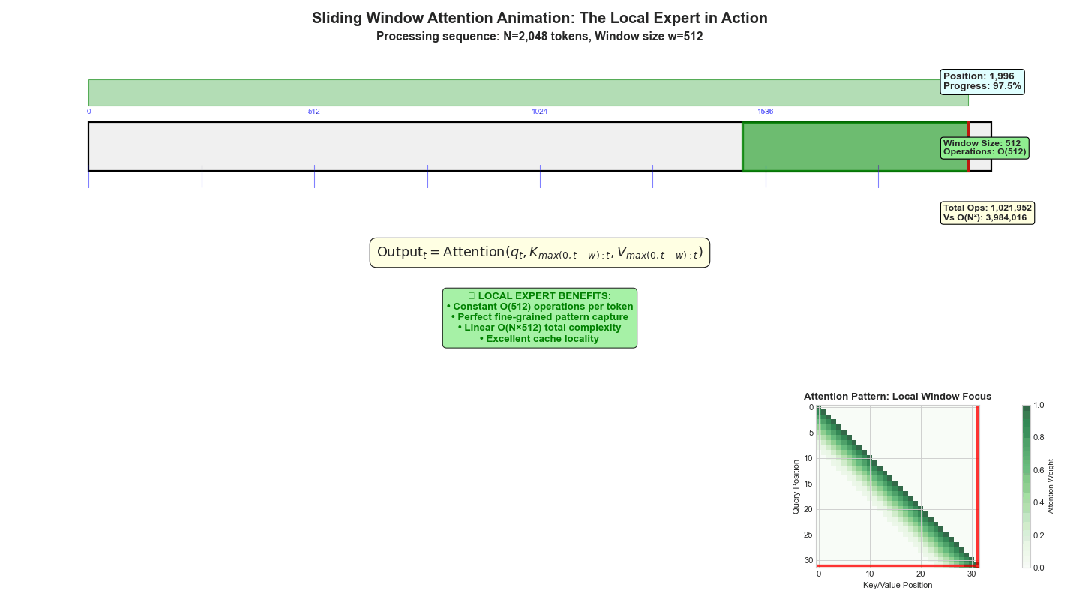
N=2048时的滑动窗口注意力示意图

计算复杂度分析： 处理单个令牌的计算成本为

O(w)

，这是一个与整体序列长度

N

无关的常数。整个序列的总计算成本为

O(N*w)

，相比标准的

O(N²)

复杂度实现了线性化的显著改进。

第二部分：压缩分支架构

设计目标： 压缩分支负责快速高效地构建整个序列历史的粗粒度全局视图，这是理解文档整体结构和主题的关键步骤。

压缩机制：从32,768令牌到2,047令牌的智能摘要

核心机制： 该算法并非简单地随机采样令牌，而是采用智能压缩策略。系统在序列上滑动大小为

l=32

的处理窗口，每次前进

d=16

个令牌位置，形成50%的重叠覆盖。这种重叠设计对于减轻块边界处的信息碎片化现象至关重要，确保生成的摘要具有良好的连续性。

摘要规模的数学计算： 生成的摘要令牌数量可以通过公式

floor((t-l)/d)

精确计算，其中

t

表示序列长度。在本例中，

t = 32,768

（完整序列长度），

l = 32

（压缩块大小），

d = 16

（压缩步长）。

计算结果为：摘要令牌数量 =

floor((32,768 - 16) / 16)

=

floor(32,752 / 16)

= 2,047

通过这一过程，原始的32,768令牌序列被转换为包含2,047个令牌的紧凑摘要表示。

基于MLP的摘要令牌生成： 每个摘要令牌通过一个小型的可学习多层感知器（MLP，论文中记为

φ

）生成。具体过程包括三个步骤：

输入阶段，内核接收包含32个原始键向量的处理块，假设头部维度

d_k

为128，则输入矩阵形状为

[32, 128]

。论文指出，为保持向量的局部顺序信息，系统会向这些向量添加块内位置编码。

转换阶段，

[32, 128]

维度的输入矩阵被送入简单的MLP网络。MLP通过多层线性变换和非线性激活函数，学习如何从32个输入令牌中提取和聚合最重要的语义信息。

输出阶段，MLP生成单个具有代表性的"摘要"键向量，输出形状为

[1, 128]

。

这一过程在所有2,047个块上重复执行，最终生成形状为

[2047, 128]

的压缩键矩阵

K_cmp

。值向量采用相同的处理流程生成压缩值矩阵

V_cmp

。

动画展示了

l=32

蓝色窗口以

d=16

令牌的步长滑动，每一步生成一个新的绿色"摘要令牌"。此过程同时应用于键（K）和值（V）向量。需要注意的是，系统并非简单平均，而是使用MLP进行智能映射，下图展示了32个键向量如何映射为1个摘要键向量的过程。

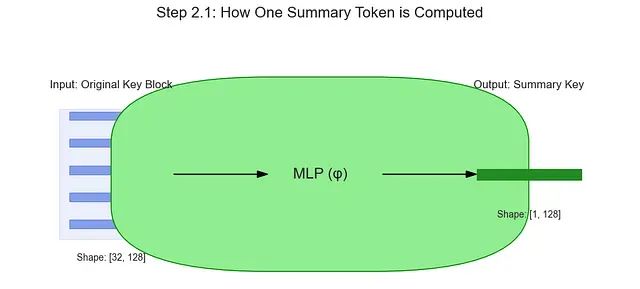
此图展示了32个键向量组成的单个块经MLP处理后生成一个摘要键向量的过程，值向量的处理方式与此相同

效率优势分析：

这里的关键技术洞察是"摘要先于注意力"的处理策略。系统首先通过线性扫描（复杂度为O(N)）创建规模更小的摘要表示，而非直接对所有

N

个令牌执行注意力计算。通过MLP进行的压缩操作具有高度可并行化的特性，相比注意力操作的计算开销很小。该过程将序列长度按步长因子

d=16

进行缩减，从32,768个令牌降至2,047个可管理的令牌规模。

摘要上的注意力计算：快速全局语义提取

设计目标： 在获得紧凑的摘要表示后，查询

q_t

需要确定摘要中与其最相关的部分，以提取全局语义信息。

实现机制： 这是标准的注意力计算过程，但由于操作对象已经大幅缩减，计算成本显著降低。已经存储在SRAM中的查询组

Q_group(t)

（包含组内所有头部的查询向量）与压缩键矩阵

K_cmp

进行矩阵乘法运算。

数学计算过程（含具体维度示例）：

查询处理：单个GQA组的查询组

Q_group(t)

形状为

[16, 128]

（16个头部，维度128）。为简化分析，考虑单头情况：

q_t

的形状为

[1, 128]

。

键矩阵：压缩键矩阵

K_cmp

的形状为

[2047, 128]

。

核心矩阵运算：执行

q_t @ K_cmp^T

操作，运算维度为

(1 x 128) @ (128 x 2047)

。

分数计算：结果为形状

[1, 2047]

的分数向量，包含每个摘要令牌相对于查询的原始重要性分数。

概率归一化：对分数向量应用Softmax函数，获得最终的注意力概率分布

p_cmp

。

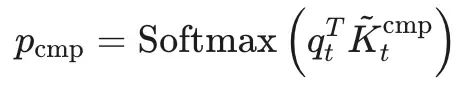
双重输出机制： 这一高效计算过程产生两个重要输出：

第一个输出是该分支的最终结果

Output_cmp

，通过

p_cmp @ V_cmp

计算得出，代表全局摘要的上下文向量表示。

第二个输出是原始注意力分数

p_cmp

，这是一个包含2,047个概率值的向量，将作为下一个分支（令牌选择）的关键输入。

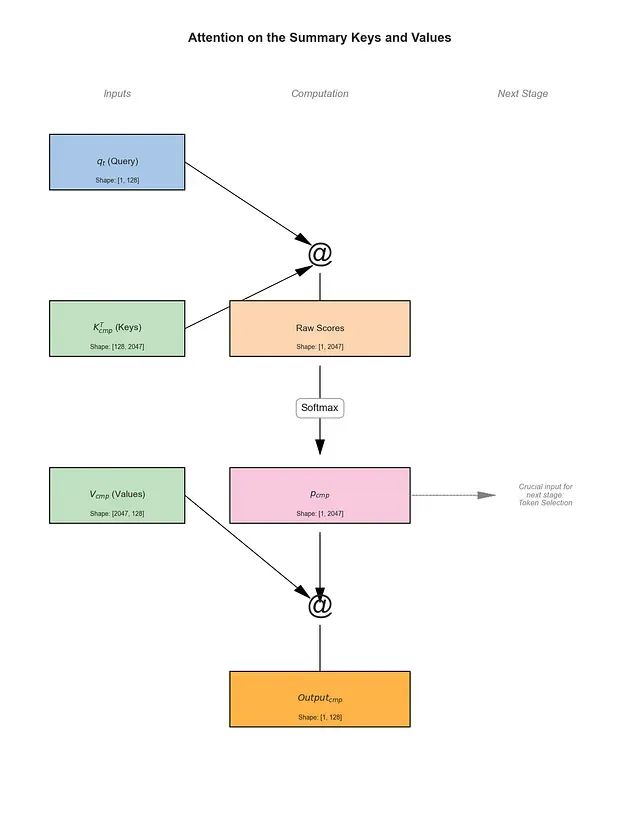
效率提升分析： 在压缩序列上执行注意力计算的成本显著降低。分数计算现在面对2,047个键而非原始的32,768个，将该步骤的计算负载减少了约16倍。这种方法将原本的O(N²)问题转换为更易处理的O(N⋅(N/d))问题，进一步简化为该分支的线性O(N)总体复杂度。

第三部分：令牌选择机制

设计目标： 令牌选择分支专注于捕获关键的长程细粒度依赖关系，通过将计算资源集中于文本中最相关的部分来实现这一目标。

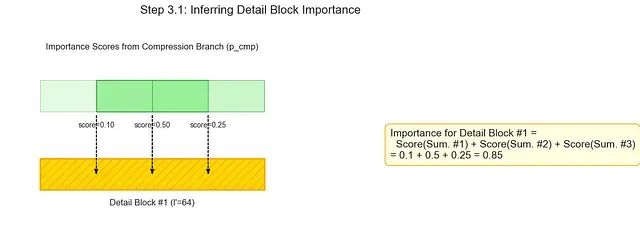
细节块重要性推断

目标定义： 高效估计512个大型细粒度块（每块大小

l'=64

）的重要性，避免执行计算密集的操作。

输入数据结构：

系统接收摘要分数向量

p_cmp

，维度为

[1, 2047]

，以及2047个压缩块与512个选择块之间的空间映射关系。

数学运算过程： 采用求和循环算法。对于512个选择块中的每个块

i

，算法通过对与其空间重叠的压缩块

j

的

p_cmp

分数进行求和来计算其重要性分数。值得注意的是，该过程生成大小为64的块（而非32），由于步长为16，需要包含前一个块和后一个块的信息。

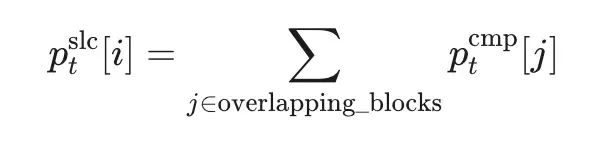
输出结果： 生成细节块重要性分数向量

p_slc

，维度为

[1, 512]

。

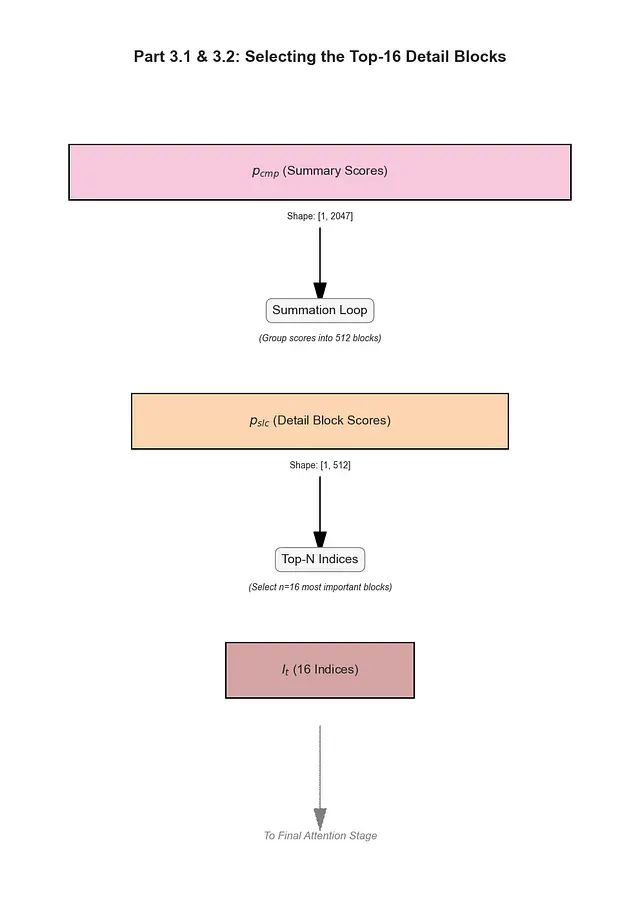
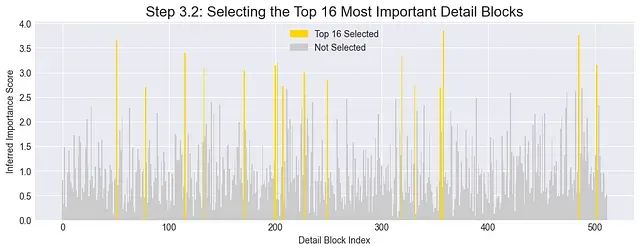
Top-N块选择策略

目标定义： 从512个候选块中选择

n=16

个最具潜力的块进行详细分析。

输入数据： 重要性分数向量

p_slc

，维度为

[1, 512]

。

算法实现： 采用简单的排序和选择操作：

I_t = top_n_indices(p_slc, n=16)

输出结果： 获得包含16个整数索引的集合

I_t

，表示最重要块的内存地址。

**
**

计算效率分析： 这些步骤在计算上几乎是零成本的。系统巧妙地重用了来自全局摘要分支的

p_cmp

概率分布，避免了在原始数据上执行新的昂贵计算。对这些分数进行求和以估计块重要性是一个极其快速的低成本操作，top-n选择过程同样轻量化。整个流程使模型能够以最小的计算代价"窥视"全局上下文并做出智能决策。

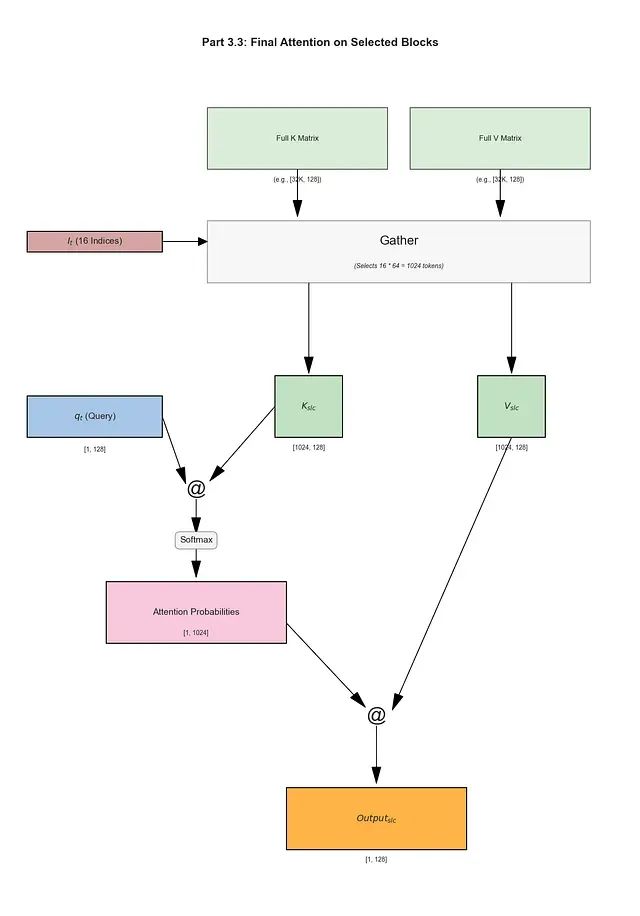
选定块的最终注意力计算

目标定义： 对最显著的原始令牌执行高保真度的注意力计算，确保重要信息的精确捕获。

输入数据结构：

查询

q_t

的维度为

[1, d_k]

或

[1, 128]

，16个获胜索引的集合

I_t

，以及用于数据收集的完整键矩阵

K

和值矩阵

V

。

数学计算流程：

收集阶段：内核获取与16个选定块对应的原始键向量和值向量，创建两个新矩阵

K_slc

和

V_slc

。

维度规格：

K_slc

的维度为

[n * l', d_k]

或

[16 * 64, 128]

→

[1024, 128]

；

V_slc

的维度为

[n * l', d_v]

或

[1024, 128]

。

注意力计算：执行

Output_slc = Attention(q_t, K_slc, V_slc)

操作。

具体运算：分数计算为

(1 x 128) @ (128 x 1024)

→

[1, 1024]

；值聚合为

(1 x 1024) @ (1024 x 128)

→

[1, 128]

。

输出结果： 生成该分支的最终向量

Output_slc

，维度为

[1, d_v]

或

[1, 128]

。

效率优势分析： 这是NSA设计的精髓所在。系统避免了对完整32,768令牌的注意力矩阵计算，转而仅对

n * l' = 1024

个最有希望的令牌执行小规模但密集的注意力计算。

在目标计算方面，成本是固定且较小的，与滑动窗口注意力的规模相当。系统仅在模型预测能产生最高影响的位置引导昂贵的高质量注意力计算。

在内存访问优化方面，该步骤利用"收集"操作模式。内核不加载完整的键值矩阵，而是从高带宽内存（HBM）执行分散读取，仅将所需的1024个向量拉入处理器的快速静态随机存取内存（SRAM）。虽然分散读取可能比单次顺序读取慢，但数据量的巨大缩减（1024对比32,768向量，约32倍减少）带来了性能的显著净收益。

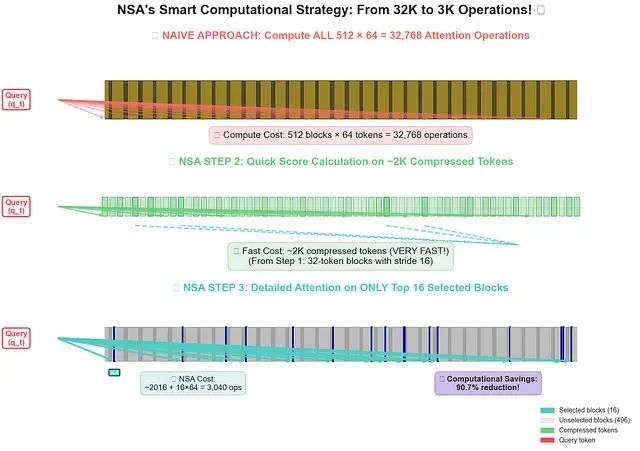
第二部分和第三部分的核心要点：压缩注意力仅对2K摘要令牌进行处理，并利用此结果从原始键值矩阵中选择1K令牌进行精确注意力计算。

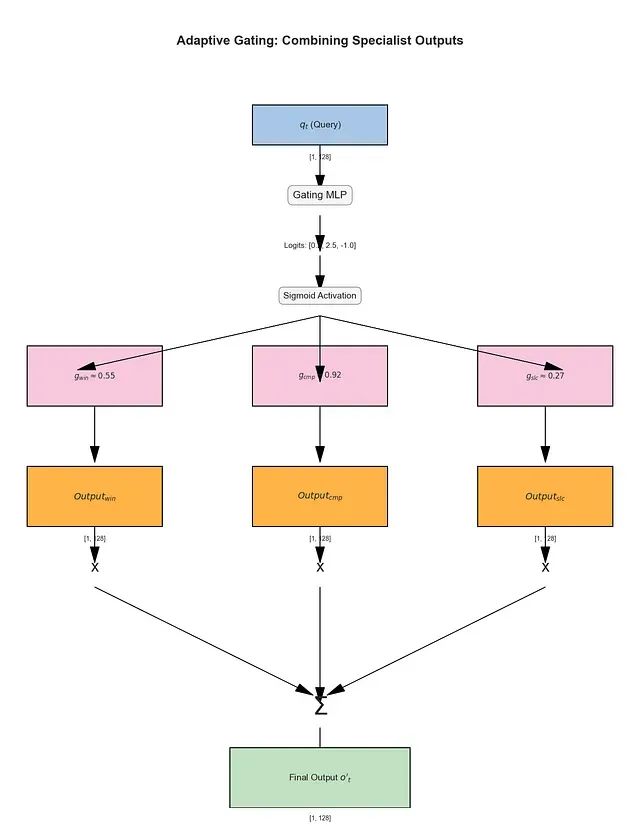
门控输出融合机制

设计目标： 智能动态地融合三个专门分支（

Output_win

、

Output_cmp

、

Output_slc

）的输出结果。相比简单平均等固定组合方式，这种动态融合机制能够实现更优的性能表现。

实现机制： 系统采用一个小型可学习的门控多层感知器，以查询

q_t

作为输入，为每个分支生成相应的"门控"分数。通过Sigmoid激活函数确保这些分数处于0到1的范围内，使其能够作为各分支输出的权重系数。

数学计算过程：

门控分数生成：小型MLP接收查询

q_t

并输出三个原始逻辑值，例如

[0.2, 2.5, -1.0]

。

Sigmoid激活应用：

g_win = sigmoid(0.2) ≈ 0.55

；

g_cmp = sigmoid(2.5) ≈ 0.92

；

g_slc = sigmoid(-1.0) ≈ 0.27

。

加权求和执行：最终输出

o*_t

通过加权求和计算，遵循论文中的方程（5）：

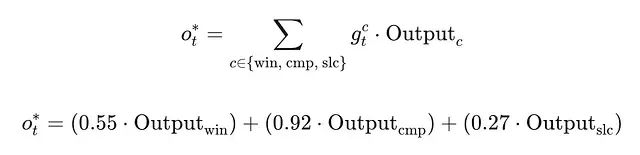
自适应优势： 该机制具有自适应特性。模型通过反向传播学习根据查询特性调整门控权重。对于需要特定事实信息的查询，模型可能学会增强

g_slc

的权重；对于关于整体主题的查询，模型可能放大

g_cmp

的影响。

硬件感知内核设计

设计目标： 将选择算法的理论效率转化为A100/H100等现代GPU上的实际性能提升。优秀的算法设计如果不考虑硬件特性，仍可能在实际执行中表现不佳。

论文的核心技术洞察在于，朴素的实现方式将受到内存带宽限制——GPU强大的计算核心将大部分时间消耗在等待数据从低速全局内存（HBM）传输上。NSA的内核设计通过三个关键策略解决这一问题。

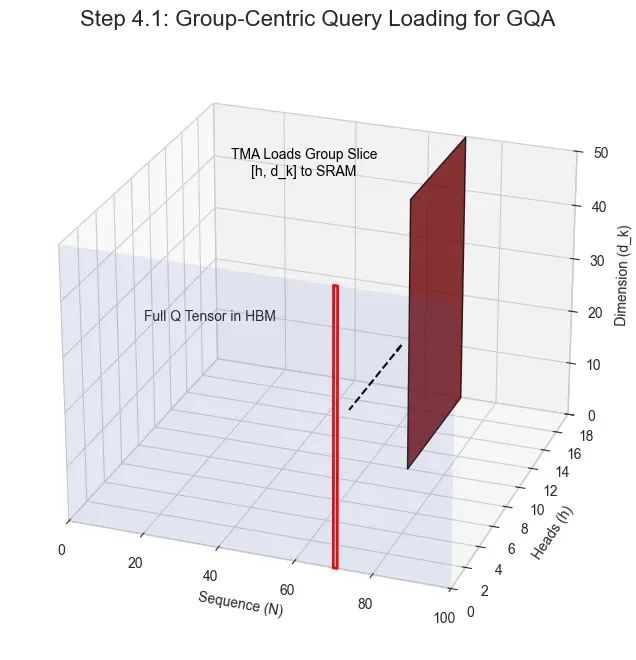
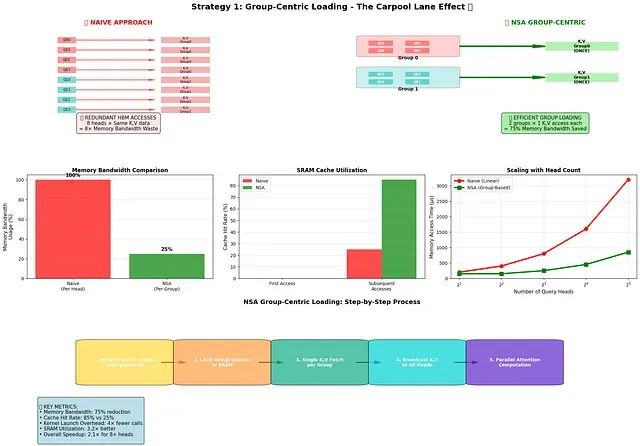
策略一：组中心化加载机制

在现代分组查询注意力（GQA）架构中，多个查询头共享相同的键和值矩阵。NSA的内核专门针对这一特性进行优化。

实现机制：系统一次性加载单个令牌位置的组内所有查询头。由于这些头都需要访问相同的选定键值块，内核可以从HBM为整个组仅执行一次数据获取操作。

技术优势：这种设计有效消除了冗余的内存传输操作，显著提升了内存访问效率。

策略二：分块处理与SRAM优化

GPU在其小容量但超高速的片上SRAM上操作数据时能够达到最佳性能表现。

实现机制：NSA内核将大规模注意力问题分解为能够适配SRAM容量的小规模"分块"。系统将Q、K、V数据的小块加载到SRAM"工作区"，在其上完成所有必要的计算操作，仅在需要新数据时才返回HBM"存储区"获取。

性能优势：这种设计最大化了数据重用效率，最小化了对低速HBM的访问次数。

策略三：融合操作与在线Softmax

在GPU上启动独立操作会产生额外的调度开销。NSA的选择注意力内核采用"融合内核"设计，将多个计算步骤合并为单一的连续操作。这种设计在Softmax计算中表现最为明显：系统不存储完整的

(h x 1024)

分数矩阵，而是采用类似FlashAttention的"在线"计算方法。

此图展示了内核在循环处理两个键值块时SRAM累加器的状态变化。

性能评估与技术验证

算法创新与硬件优化的结合使NSA在实际应用中实现了显著的性能提升。

计算效率表现： 论文的基准测试结果显示，对于64k长度的序列，NSA相对于高度优化的FlashAttention-2基线实现了惊人的加速效果。在解码阶段实现了11.6倍的速度提升，前向传播过程中达到9.0倍加速，反向传播阶段获得6.0倍的性能改进。

内存效率优化： 解码阶段的加速直接源于内存访问量的显著减少。NSA大幅降低了需要从内存加载的键值缓存数据量，从而有效缓解了内存带宽瓶颈。

模型性能验证： 更高的计算速度如果以模型能力下降为代价则失去了实际意义。NSA通过实验证明了性能与效率的双重优化是可能的。NSA训练的模型在涵盖通用知识、推理能力和编程任务的综合基准测试中达到或超越了全注意力基线的表现水平。

在长上下文任务处理方面，NSA在LongBench基准测试中显著优于其他稀疏方法和全注意力基线。特别值得关注的是，NSA在64k上下文长度的"大海捞针"测试中达到了完美的准确率，证明了其在保持细粒度信息方面的卓越能力。

NSA不仅在效率方面表现出色，在复杂推理任务中更是展现了超越基线方法的能力。在GSM8K数学应用题基准测试中，NSA获得了0.520的分数，相比全注意力方法的0.486实现了显著提升。在LongBench长上下文任务基准测试中，NSA达到了0.469的最高平均分，优于Exact-Top基线的0.423、Quest的0.392、infLLM的0.383、H2O的0.303以及全注意力模型的0.437。在AIME竞赛数学任务中，经过数学推理监督微调的NSA-R模型大幅超越了全注意力-R模型，在16k生成限制下分别获得0.146和0.092的分数。

论文分析认为，这种性能提升源于稀疏机制强制模型专注于最重要的信息，有效过滤了噪声信息并增强了推理路径的质量。

总结

原生稀疏注意力机制远超传统的渐进式技术改进，代表了高效AI模型设计的根本性范式转变。这一技术突破建立在两个核心技术原则之上。

首先是算法智能化设计原则。NSA避免了暴力计算的简单路径，通过构建本地、摘要和详细三个层次的分层视图，在最适合的粒度级别高效处理信息。计算资源的重用策略，特别是摘要分数指导详细搜索的机制，成为其设计理念的重要特征。

其次是算法与硬件的协同优化原则。算法的实际性能完全取决于其实现质量。NSA的技术成功源于其计算步骤与现代GPU架构优势的完美匹配——通过最小化低速内存访问并保持强大计算核心的高利用率，实现了理论优势向实际性能的有效转化。

通过同时掌握这两个关键要素，NSA实现了技术发展的最终目标：以极小的计算成本处理大规模上下文信息，同时达到最先进的性能水平。这为未来的技术发展提供了强有力的指导框架，证明了构建更强大和更可扩展AI系统的路径不仅在于增大模型规模，更在于构建更智能、更高效的技术架构。

参考文献

[1] Yuan, J., Gao, H., Dai, D., et al. (2025). Native Sparse Attention: Hardware-Aligned and Natively Trainable Sparse Attention. arXiv:2502.11089v2.

https://avoid.overfit.cn/post/bc344f1bc3914fc1a065475587dc7ce8

作者：yugandhar nanda