【动态规划算法】路径问题
什么是动态规划算法
动态规划(Dynamic Programming,简称 DP)是一种通过分解复杂问题为重叠子问题,并存储子问题的解以避免重复计算,从而高效求解具有特定性质(重叠子问题、最优子结构)问题的算法思想。
一、核心思想:“分解 + 复用”
动态规划的核心在于:
1.将原问题拆解为规模更小的子问题;
2.求解子问题后,将结果存储起来(记忆化),避免后续重复计算;
3.基于子问题的解,推导出原问题的解。
简单来说,就是 “用已知的子问题答案,解决未知的大问题”,本质是用空间换时间。
二、动态规划的 2 个关键前提
只有当问题满足以下两个条件时,才能用动态规划求解:
- 重叠子问题
问题可以分解为多个重复出现的子问题。
例如:计算斐波那契数列 f(n) = f(n-1) + f(n-2) 时,f(5) 依赖 f(4) 和 f(3),f(4) 又依赖 f(3) 和 f(2)——f(3) 就是被重复计算的重叠子问题。- 最优子结构(Optimal Substructure)
问题的最优解包含子问题的最优解。
例如:求 “从 A 到 B 的最短路径” 时,若路径 A→C→B 是最优解,则 A→C 和 C→B 一定分别是 A 到 C、C 到 B 的最短路径(子问题的最优解)。
三、动态规划的 2 种实现方式
动态规划通常有两种实现思路,核心都是 “存储子问题的解”,只是顺序不同:
- 自顶向下(Top-Down):递归 + 记忆化
思路:从原问题出发,递归分解为子问题,用备忘录(数组或哈希表) 存储已求解的子问题答案,避免重复计算。- 自底向上(Bottom-Up):迭代 + DP 表
思路:从最小的子问题开始,按顺序求解,用DP 表(数组) 记录子问题的解,逐步推导出原问题的解。
四、经典应用场景
动态规划广泛用于求解 “最优问题” 或 “计数问题”,典型案例包括:
计数问题:爬楼梯(方法数)、不同路径(网格中路径数);
最优问题:最长公共子序列(LCS)、最大子数组和、0-1 背包问题(最大价值);
其他:编辑距离(字符串相似度)、打家劫舍(不相邻房屋最大金额)等。
五、动态规划与其他算法的区别
与递归:递归可能重复计算子问题,动态规划通过记忆化避免重复,效率更高;
与贪心算法:贪心只做局部最优选择,不依赖子问题的解;动态规划则基于子问题的最优解推导全局最优;
与分治法:分治法(如归并排序)的子问题不重叠,无需存储解;动态规划的子问题重叠,必须存储解。
一. (62.)不同路径(力扣)

1.1算法原理
- 状态表⽰:
对于这种「路径类」的问题,我们的状态表⽰⼀般有两种形式:
i. 从 [i, j] 位置出发,巴拉巴拉;
ii. 从起始位置出发,到达 [i, j] 位置,巴拉巴拉。
这⾥选择第⼆种定义状态表⽰的⽅式:
dp[i][j] 表⽰:⾛到 [i, j] 位置处,⼀共有多少种⽅式。
- 状态转移⽅程:
从最近的一步将问题划分为子问题,再由若干个子问题来来解决总问题。dp[i][j] 表⽰到达 [i, j] 位置的⽅法数,到达 [i, j] 位置之前的⼀⼩步,有两种情况:
i. 从 [i, j] 位置的上⽅( [i - 1, j] 的位置)向下⾛⼀步,转移到 [i, j] 位置;
ii. 从 [i, j] 位置的左⽅( [i, j - 1] 的位置)向右⾛⼀步,转移到 [i, j] 位置。
由于我们要求的是有多少种⽅法,因此状态转移⽅程就呼之欲出了: dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 。为什么方法数不将这一小步也加上?
因为这一小步不是方法数,而是一种方法中延申的一步,是路长步数,不影响方法数
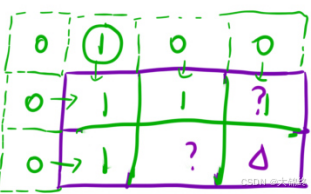
3.初始化
通过添加虚拟节点来避免复杂边界问题讨论,需注意:
1.虚拟节点的值要保证后续填表是正确的
2.下标映射关系
在左上角第一个位置的上边或左边初始化为1,其他地方初始化为0,就不会影响后续填表
- 填表顺序:
根据状态转移⽅程的推导来看,填表的顺序就是从上往下填每⼀⾏,在填写每⼀⾏的时候从左往右。
- 返回值:
根据状态表⽰,由于多增加了一行一列的虚拟节点,我们要返回 dp[m][n] 的值(原本返回坐标为m-1,n-1)。
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m+1,vector<int>(n+1));//初始化dp表的虚拟节点一行一列,将[0][1]或[1][0]位置赋1即可其他默认为0dp[1][0]=1;//填表for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){dp[i][j]=dp[i-1][j]+dp[i][j-1];}}return dp[m][n];}
};
二. (63.) 不同路径 II(力扣)

2.1算法原理
- 状态表示:
dp[i][j] 表⽰:⾛到 [i, j] 位置处,⼀共有多少种⽅式。
- 状态转移:
到达 [i, j] 位置之前的⼀⼩步,有两种情况:
i. 从 [i, j] 位置的上⽅( [i - 1, j] 的位置)向下⾛⼀步,转移到 [i, j] 位置;
ii. 从 [i, j] 位置的左⽅( [i, j - 1] 的位置)向右⾛⼀步,转移到 [i, j] 位置。
但是, [i - 1, j] 与 [i, j - 1] 位置都是可能有障碍的,此时从上⾯或者左边是不可能到达 [i, j] 位置的,也就是说,此时的⽅法数应该是 0。若dp[i][j]位置本身就有障碍物方法数直接为0
由此我们可以得出⼀个结论,只要这个位置上有障碍物,那么我们就不需要计算这个位置上的值,直接让它等于 0 即可。
3.初始化
通过添加虚拟节点来避免复杂边界问题讨论,需注意:
1.虚拟节点的值要保证后续填表是正确的
2.下标映射关系
在左上角第一个位置的上边或左边初始化为1,其他地方初始化为0,就不会影响后续填表
- 填表顺序:
根据状态转移⽅程的推导来看,填表的顺序就是从上往下填每⼀⾏,在填写每⼀⾏的时候从左往右。
- 返回值:
根据状态表⽰,由于多增加了一行一列的虚拟节点,我们要返回 dp[m][n] 的值(原本返回坐标为m-1,n-1)。
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int n=obstacleGrid.size(),m=obstacleGrid[0].size();vector<vector<int>> dp(n+1,vector<int>(m+1));//初始化dp[0][1]=1;//填表for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(obstacleGrid[i-1][j-1]!=1)dp[i][j]=dp[i-1][j]+dp[i][j-1];}}return dp[n][m];}
};
三. 剑指 Offer 47. 礼物的最大价值(力扣)

3.1算法原理
1.状态表示:
dp[i][j] 表⽰:⾛到 [i, j] 位置处,此时的最⼤价值。
- 状态转移⽅程:
对于 dp[i][j] ,想要到达 [i, j] 位置,有两种⽅式:
i. 从 [i, j] 位置的上⽅ [i - 1, j] 位置,向下⾛⼀步,此时到达 [i, j] 位置能
拿到的礼物价值为 dp[i - 1][j] + grid[i][j] ;
ii. 从 [i, j] 位置的左边 [i, j - 1] 位置,向右⾛⼀步,此时到达 [i, j] 位置能
拿到的礼物价值为 dp[i][j - 1] + grid[i][j]
我们要的是最⼤值,因此状态转移⽅程为:
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]
3.初始化
1.依旧是添加一行一列的虚拟节点,需注意的是与前两道题不同的是前两题求的是路径,本题求的是每个节点的“价值”,所以不能让虚拟节点影响到原本节点的价值,由状态转移方程可知,求一个节点的最大价值,总共有两种路径取大的一方,题目要求所有值都>=0,所以将所有虚拟节点初始化为0就没有影响
2.保证后续填表正确,注意dp表与原数组下标的映射关系
- 填表顺序:
从上往下填写每⼀⾏,每⼀⾏从左往右。
5.返回值
由于多添加了一行一列的虚拟节点,返回 dp[m][n] 的值
class Solution {
public:int jewelleryValue(vector<vector<int>>& f) {int m=f.size(),n=f[0].size();vector<vector<int>> dp(m+1,vector<int>(n+1));//填表,初始化虚拟节点为0自动完成for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){dp[i][j]=max(dp[i-1][j],dp[i][j-1])+f[i-1][j-1];}}return dp[m][n];}
};
四. (931.) 下降路径最小和(力扣)

4.1算法原理
- 状态表⽰
dp[i][j] 表⽰:到达 [i, j] 位置时,所有下降路径中的最⼩和。
- 状态转移⽅程:
对于普遍位置 [i, j] ,根据题意得,到达 [i, j] 位置可能有三种情况:
i. 从正上⽅ [i - 1, j] 位置转移到 [i, j] 位置;
ii. 从左上⽅ [i - 1, j - 1] 位置转移到 [i, j] 位置;
iii. 从右上⽅ [i - 1, j + 1] 位置转移到 [i, j] 位置;
我们要的是三种情况下的「最⼩值」,然后再加上矩阵在 [i, j] 位置的值。
于是 dp[i][j] = min(dp[i - 1][j], min(dp[i - 1][j - 1], dp[i - 1][j + 1])) + matrix[i][j]
3.初始化
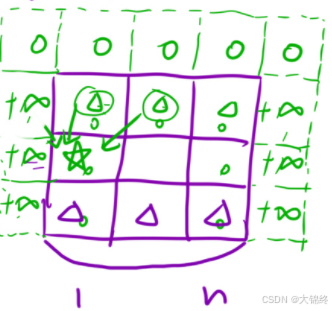
与前几道题增加一行一列的初始化不同,本题要增加两列一行,因为当前位置值受上一行左中右三个值的影响,所以原数组中最右边一列的值也面临初始化的问题,所以也需要增加虚拟节点
1.因为所求为下降路径的最小和,所以除第一行外的其他虚拟节点需要初始化为正无穷大,同时原数组第一行没有之前的下降路径,所以不能受虚拟节点的影响,第一行虚拟节点要设为0。
2.可以采取先将全部虚拟节点初始化为正无穷大然后将第一行改为0
- 填表顺序:
从上往下
- 返回值:
注意这⾥不是返回 dp[m][n] 的值!
题⽬要求只要到达最后⼀⾏就⾏了,因此这⾥应该返回 dp 表中最后⼀⾏的最⼩值
class Solution {
public:int minFallingPathSum(vector<vector<int>>& m) {int x=m.size(),y=m[0].size();vector<vector<int>> dp(x+1,vector<int>(y+2,INT_MAX));//初始化for(int j=0;j<=y+1;j++){dp[0][j]=0;}//填表for(int i=1;i<=x;i++){for(int j=1;j<=y;j++){dp[i][j]=min({dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1]})+m[i-1][j-1];}}//找到最小返回值int ret=INT_MAX;for(int i=x,j=1;j<=y;j++){if(dp[i][j]<ret) ret=dp[i][j];}return ret;}
};
五. (64.) 最小路径和(力扣)

5.1算法原理
- 状态表⽰:
dp[i][j] 表⽰:到达 [i, j] 位置处,最⼩路径和是多少。
- 状态转移:
表⽰到达 到达 [i, j] 位置处的最⼩路径和,那么到达[i, j] 位置之前的⼀⼩步,有两种情况:
i. 从 [i - 1, j] 向下⾛⼀步,转移到 [i, j] 位置;
ii. 从 [i, j - 1] 向右⾛⼀步,转移到 [i, j] 位置。
由于到 [i, j] 位置两种情况,并且我们要找的是最⼩路径,因此只需要这两种情况下的最⼩值,再加上 [i, j] 位置上本⾝的值即可。
也就是: dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]
- 初始化:
添加⼀⾏,并且添加⼀列后,所有位置的值可以初始化为⽆穷⼤,然后让
dp[0][1] = dp[1][0] = 1 即可。(因为求的是最小值,不能让虚拟节点干扰)
- 填表顺序:从上往下填每⼀⾏,每⼀⾏从左往后
- 由于多加了一行一列的虚拟节点,返回dp[m][n]
class Solution {
public:int minPathSum(vector<vector<int>>& g) {int m=g.size(),n=g[0].size();//创建dp表顺便初始化vector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));//特殊初始化值dp[1][0]=dp[0][1]=0;//填表for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){dp[i][j]=min(dp[i-1][j],dp[i][j-1])+g[i-1][j-1];}}return dp[m][n];}
};
六. (174.) 地下城游戏(力扣)

6.1算法原理
- 状态表⽰:
这道题如果我们定义成:从起点开始,到达 [i, j] 位置的时候,所需的最低初始健康点数。那么我们分析状态转移的时候会有⼀个问题:那就是我们当前的健康点数还会受到后⾯的路径的影响。也就是从上往下的状态转移不能很好地解决问题。
这个时候我们要换⼀种状态表⽰:从 [i, j] 位置出发,到达终点时所需要的最低初始健康点数。这样我们在分析状态转移的时候,后续的最佳状态就已经知晓。
综上所述,定义状态表⽰为:
dp[i][j] 表⽰:从 [i, j] 位置出发,到达终点时所需的最低初始健康点数
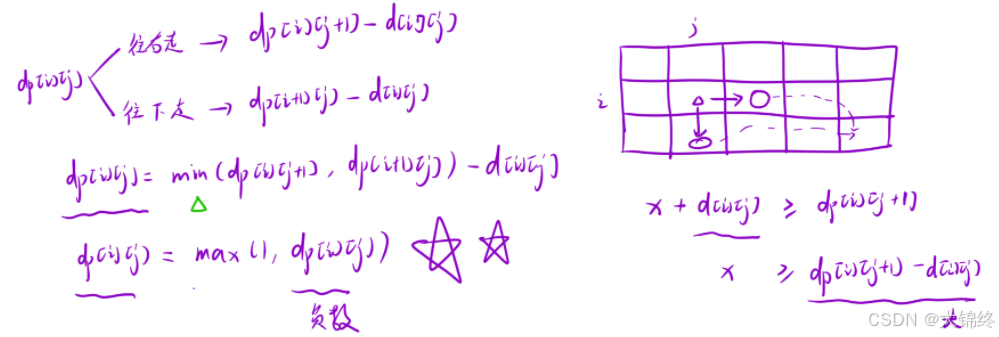
- 状态转移⽅程:
在 [i, j] 位置的最低健康点数加上这⼀个位置的消耗,应该要⼤于等于右边或下边位置的最低健康点数。(图中d代表dungeon)
dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j]
注意:
如果当前位置dungeon[i][j] 是⼀个⽐较⼤的正数的话, dp[i][j] 的值可能变
成 0 或者负数。也就是最低点数会⼩于 1 ,那么骑⼠就会死亡。因此我们求出来的 dp[i][j] 如果⼩于等于 0 的话,说明此时的最低初始值应该为 1 。处理这种情况仅需让 dp[i][j] 与 1 取⼀个最⼤值即可:dp[i][j] = max(1, dp[i][j])
- 初始化:
由于节点状态表示与前面题不同,初始化方式也改变,每个节点依赖后一个下位置和右位置节点的值,在 dp 表最后⾯添加⼀⾏,并且添加⼀列后,所有的值都先初始化为⽆穷⼤(因为求最小值不能被虚拟节点影响),然后让dp[m][n - 1] = dp[m - 1][n] = 1 (终点房间所依赖的下一个位置,最小值为1根据题目要求,不然没法进行下去和其他虚拟节点不同)。
4.填表顺序:
发生变化,要从下往上填每⼀⾏,每⼀⾏从右往左
- 返回值:
根据状态表⽰,需要返回 dp[0][0] 的值
class Solution {
public:int calculateMinimumHP(vector<vector<int>>& d) {int m=d.size(),n=d[0].size();vector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));//特殊初始化dp[m][n-1]=dp[m-1][n]=1;//填表for(int i=m-1;i>=0;i--)//注意下标映射关系没有变{for(int j=n-1;j>=0;j--){dp[i][j]=min(dp[i+1][j],dp[i][j+1])-d[i][j];dp[i][j]=max(1,dp[i][j]);//防止为负数}}return dp[0][0];}
};