当前位置：首页 > news >正文

控制建模matlab练习04：二阶系统的时域响应

news 2025/8/4 7:13:36

此练习主要是典型的二阶系统时域响应的分析和建模。
包括两部分：
①对经典响应的建模分析；
②阻尼比对系统响应的影响；

一、对经典响应的建模分析

此过程跟上一篇一阶系统的，非常类似。
1、单位冲激响应；
2、单位阶跃响应；
3、对初始条件响应；

01在matlab中表示如下图的系统

先假设以下有这个二阶系统的形式：

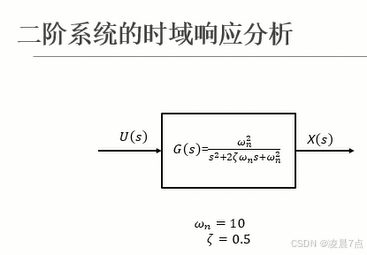
图中已知，系统的传递函数G(s)，则在matlab中用代码表示出来：
（基本与上一篇一阶系统的相同，主要的不同，在于二阶的部分推导）

clc;clear;close all;
%%定义二阶系统
zeta=0.5;
w_n=10;
G_s = tf([w_n^2],[1,2*w_n*zeta,w_n^2]);
%第一个[w_n^2]是分子部分；第二个[[1,2*w_n*zeta,w_n^2]分别是分子s^2、s和1的系数部分；
%所以这里G_s就是传递函数；%% 绘图
subplot(3,1,1) %3行1列三幅图，三个图的第1幅图
impulse(G_s);%% 单位冲激响应subplot(3,1,2) %3行1列三幅图，三个图的第2幅图
step (G_s);%% 单位阶跃响应subplot(3,1,3) %3行1列三幅图，三个图的第3幅图
A = [[0 1];[-w_n^2 -2*zeta*w_n]];
B = [0 ; w_n^2];
C = [1 0]; 
D =0; 
sys = ss(A,B,C,D);
z0 = [1;0];      %定义初始条件为[1;0]；
initial(sys,z0); %对初始状态的响应，因为这个initial是只对状态空间方程的
% - 因为**传递函数**的推导，是以**零初始条件**为基础的。
% -  所以在求**对有初始条件**的响应时，需将系统**用状态空间方程**的形式。

其中，从传递函数推导到状态空间方程的部分过程如下图：

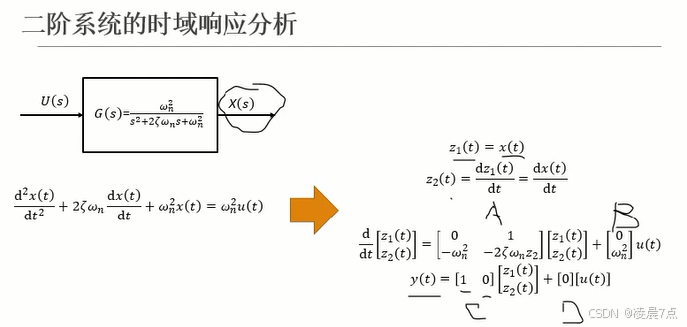
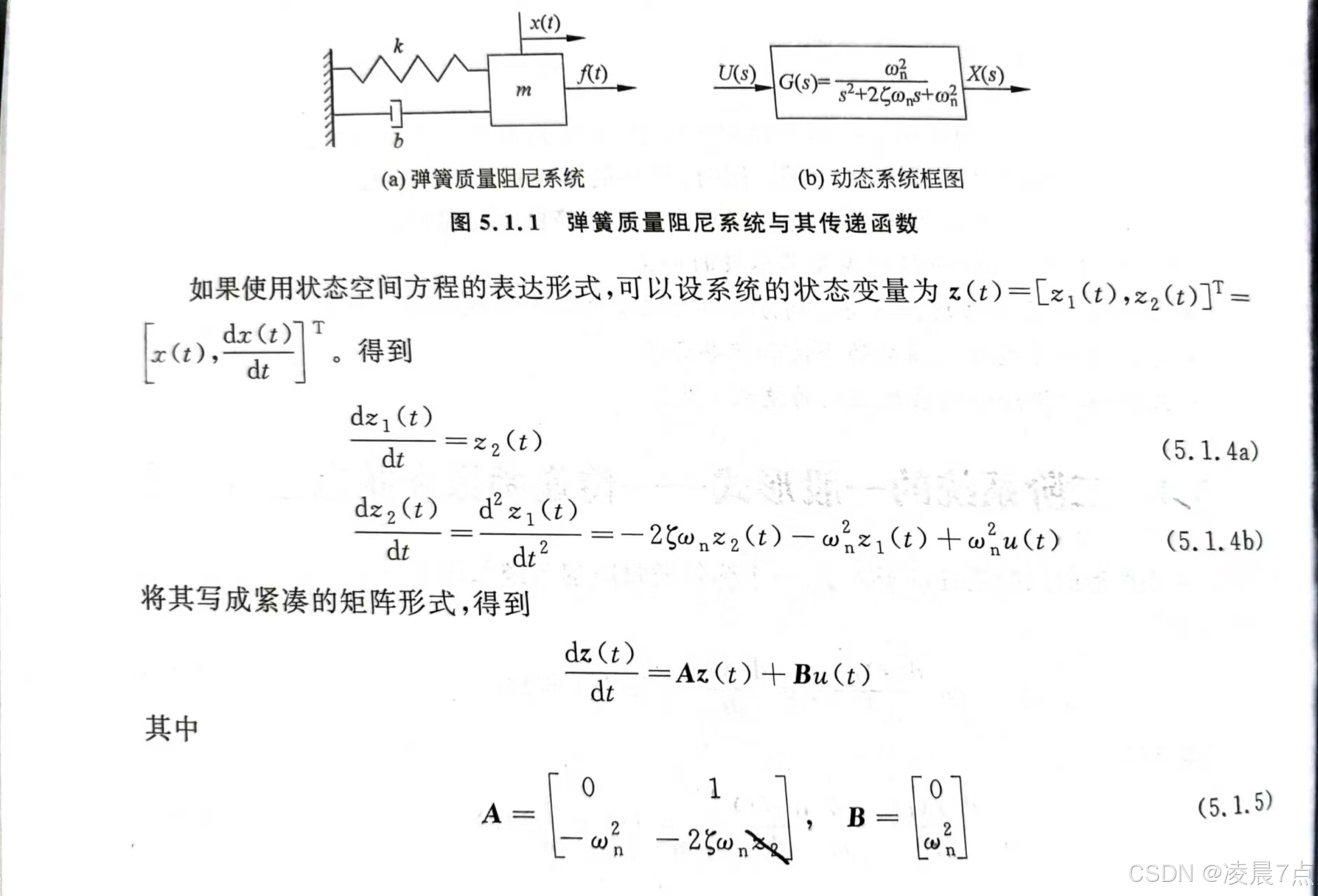
部分推导过程

02结果与分析

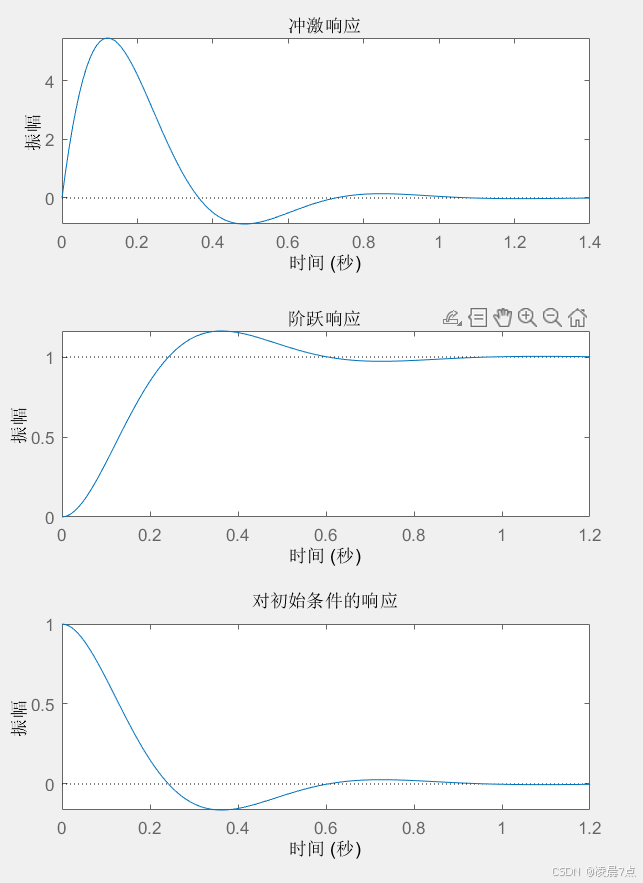
运行之后：仿真结果图。
分析：

二、阻尼比对系统响应的影响.

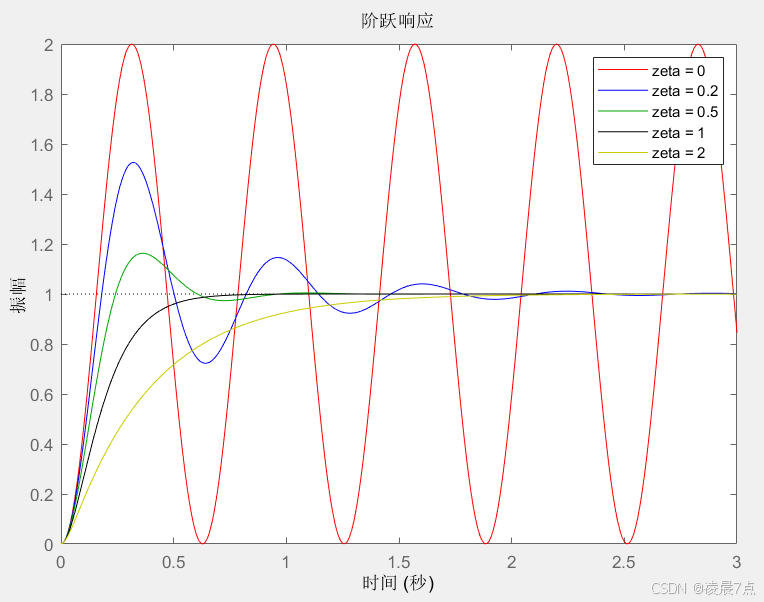
01在matlab中建立不同zeta的模型

阻尼比zeta，是非常重要的参数，它确定了系统的表现。
下面代码分析一下不同阻尼比，对单位阶跃响应的不同表现。

clc;clear;close all;
%%定义参数
zeta = [0, 0.2, 0.5, 1, 2];%这里zeta不止一个0.5，而是一个数列，这样就可以调取不同zeta来比较
w_n = 10;%% 求每一组zeta的单位阶跃响应
t = 0:0.01:3;%这里给统一时间范围
colorcode = ['r', 'b', 'g', 'k', 'y'];%用不同颜色表示不同zeta更清晰
for i =1:length(zeta)hold on;%这里可以让下一个值，生成下一幅图的时候，是会放在同一个图上的G = tf([w_n^2],[1,2*w_n*zeta(i),w_n^2]);step(G,t,colorcode(i));
end 
legend ('zeta = 0', 'zeta = 0.2','zeta = 0.5','zeta = 1','zeta = 2');