PID控制原理分析及应用（稳态误差详细分析）（一）

---

1、PID算法

PID是比例（Proportional）、积分（Integral）、微分（Differential）的缩写。

1.1 整体分析

PID是一种闭环控制算法，它动态改变施加到被控对象的输出值（Out），使得被控对象某一物理量的实际值（Actual），能够快速、准确、稳定地跟踪到指定的目标值（Target）。

就是我们利用这个算法，实现我们想要的结果，也就是将实际值始终追踪到目标值。
假设我们控制温度，我的目标值就是我想要的温度，我的实际值就是实际输出的温度，我想要的结果就是我的实际输出值始终是我的目标值这种完美的控制。但是实际是很难的。因此我们需要控制。
那输出值是什么？
我们控制温度，注意我们的控制对象不是温度，稳定是我们想要的结果，什么是我们控制的对象呐，是加热管或者是其他发热元器件。所以才有动态改变施加到被控对象的输出值，我们的被控对象是加热管，那么加热管的输出值是什么，那就是开的时间。被控对象
某一个物理量指的温度，这样就相当于是能够快速准确稳定地跟踪到指定的目标值。

所以从这里我们可以理解了，我们在实际控制过程中需要抽象出执行结构或者是被控对象，并且这个地方很容易分析，我们想要控制温度，那么我们控制的是加热管产生温度。对于我们有两个已知变量，一个是实际值，一个是目标值，但是我们需要计算的是输出值。换句话说，这个输出值一方面指的是是PID的输出值，另一方面也就是加热管输出的时间值，用于我们控制加热管的开启时间。

控制回路路径​：设定温度（Target） → 温度传感器测量实际值（Actual） → 控制器计算误差（Error = Target - Actual） → PID算法生成输出值（Out） → 执行机构调节功率 → 温度变化。

在温度控制中，​输出值（Out）是PID控制器生成的动态功率指令，其本质是 ​​“能量调节开关”​​ 的量化信号：

• ​物理载体​：电压、PWM占空比、阀门开度等；
• ​核心作用​：通过比例、积分、微分的协同，将输出值转化为恰如其分的加热/制冷功率，驱动温度精准、稳定地跟踪设定值。
  理解输出值的关键在于抓住其 ​​“误差驱动”与“功率映射”​​ 的双重属性——它既是算法的计算结果，也是物理世界的能量闸门。

能量调节开关很形象，实际与目标的区别是通过PID控制的能量调节开关有关系。

这里有一个难点是，怎么将我们已知的温度、速度、湿度等具有现实意义的数据经过PID转换为对应的“量调节开关”，例如是电压、电流、阀门开度。

PID是一种基于误差（Error）调控的算法，其中规定：误差=目标值-实际值，PID的任务是使误差始终为0。

PID对被控对象模型要求低，无需建模，即使被控对象内部运作规律不明确，PID也能进行调控。

1.2 开环与闭环

开环（Open Loop）：控制器单向输出值给被控对象，不获取被控对象的反馈，控制器对被控对象的执行状态不清楚。

闭环（Closed Loop）：控制器输出值给被控对象，同时获取被控对象的反馈，控制器知道被控对象的执行状态，可以根据反馈修改输出值以优化控制。

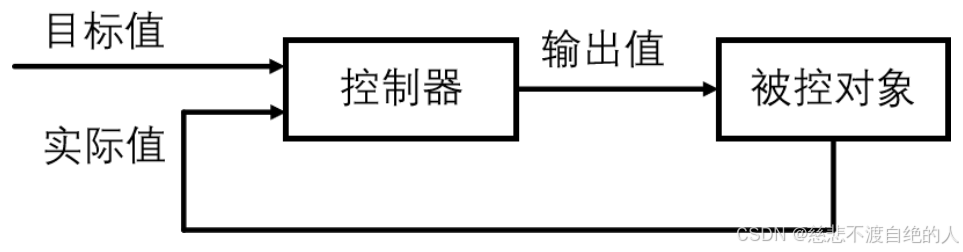
控制器值得就是PID或者其他算法。被控对象就是加热管、电机等，而输出值其实就是我们需要通过物理载体来进行控制加热管、电机这些。例如电流或者电压会加热管的影响，或者对电机的影响，使其加热管的输出温度改变，或者是电机的速度改变。这个地方需要反复的强化自己。

以电机为例，当负载发生变化或者是电压或者电流发生变化，均会影响其速度，那么我们通过变化量告诉PID，我现在变了，需要你调节，至于怎么运算是PID的现在先不考虑，反正最终PID会告诉我们一个值例如是我告诉你你现在应该给我加大多少电流或者是功率，然后按照这个给我再次驱动电机，这样电机的速度就会因为输入的电流或者电压大小来影响我们想要的速度的大小。这个PID告诉我们应该怎么调整电机的输入值就是相当于是我们前面叙述的“能量调节开关”。

举几个例子：
被控对象：锅炉，目标值和期望值：温度（传感器获取）， 输出值：燃料供给速度。
被控对象：汽车， 目标值和期望值：汽车在车道的横向位置（要求汽车走直线）， 输出值：方向盘角度。
被控对象：火箭， 目标值和期望值：刚开始要求角度和地面垂直，然后在与地面呈现一定夹角（火箭姿态传感器获取）， 输出值：火箭矢量发动机喷射方向。

智能小车，差速控制进行转弯。

核心还是怎么转换。

1.3 PID公式

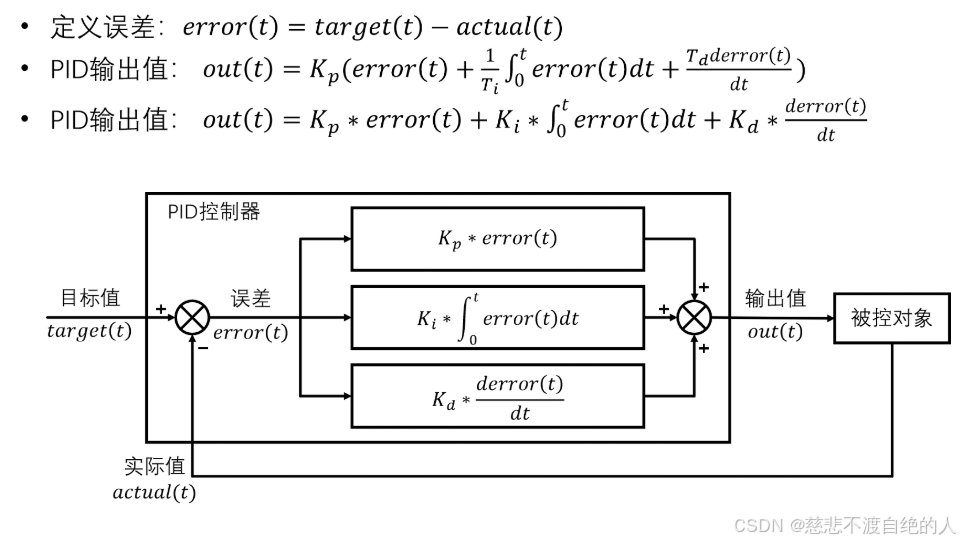
这个公式是具有数学意义与物理意义的，后续结合系统的校正（自动控制原理）进行详细的分析与阐述。当前阶段就是学会应用。

在自控原理这本书中有典型的输入信号，例如单位阶跃函数、单位斜波函数、单位加速度函数、单位脉冲函数、正弦函数等，这些典型的输入信号，是根据系统常遇到的输入信号形式，再数学描述上加以理想化的一些基本输入函数。说白就是将输入信号建立数学模型。

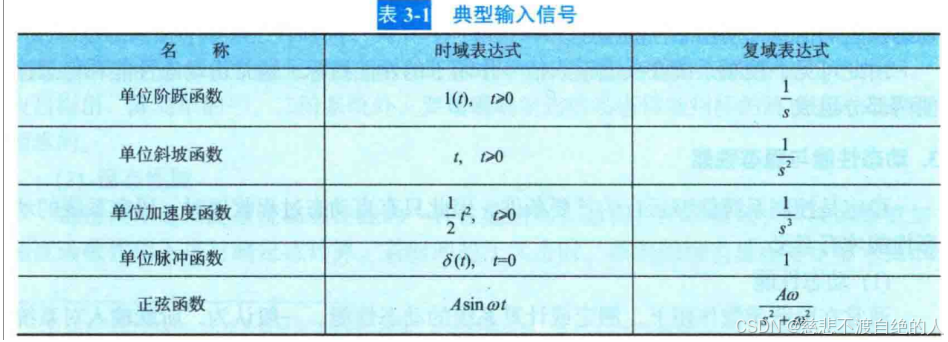
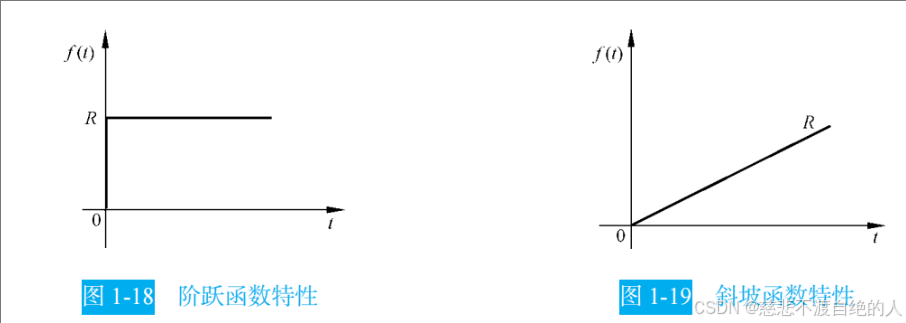
脉冲函数还是不怎么使用的，如：瞬态分析​：测试电源波动、开关噪声对电路的影响（如EMC抗扰度测试）；

我们控制温度的时候，一般使用的是阶跃函数（而非脉冲函数）是更常用的典型输入信号。
物理意义匹配​：
阶跃信号（如设定值突然从30℃跳变至100℃）能准确模拟温度控制中的常见扰动，例如加热设备开机、设定值调整或负荷突变。这类突变在实际工业场景（如注塑机加热、热处理炉）中频繁发生。
工业温控器（如PID控制器）的调试通常依赖阶跃响应：

• ​自整定功能​：
  设备通过注入阶跃信号，观察响应曲线自动计算PID参数（如比例带、积分时间），实现“无超调、无欠调”控制。
• ​稳态误差分析​：
• 阶跃输入下，稳态误差直接反映系统抗扰能力（如加热功率波动补偿）。

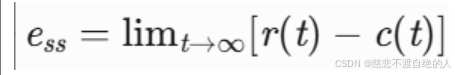
1.3.1 比例项

只含有比例项的PID输出值：

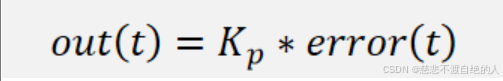
比例项的输出值仅取决于当前时刻的误差，与历史时刻无关。当前存在误差时，比例项输出一个与误差呈正比的值，当前不存在误差时，比例项输出0。

K_p越大，比例项权重越大，系统响应越快，但超调也会随之增加。

纯比例项控制时，系统一般会存在稳态误差，K_p越大，稳态误差越小。

Kp表示的就是调节力度，就是可以快速调节，水多加面，面多加水。

在这里简单分析一下，我们不管是电机调速还是温度控温，其实我们对于被控对象的了解是一个黑盒子，也就是说我们只是知道我们把电流或者电压或者PWM脉宽变长速度就会增大，或者把加热管的时间开的长一点温度就会升上来，这个过程是应该有一个传递函数的，但是由于我们在实际工程中基本是不关注的，更不会关注他的零极点，因为如果对其进行建模，那么就会很复杂，有一点舍本逐末。

我们使用PID调节的过程，其实就是对这个被控对象的零极点就行调节位置，也正是因为我们利用了PID的调节，使得系统的零极点达到了我们想要的控制系统。换句话说，我们在不知道系统传递的函数情况下一样可以调节系统，这是因为我们不关注对零极点是怎么移动的，因为不管怎么移动最终我们肯定是要让我们的输出数据曲线满足我们想要的，所以这也是PID为什么好用的思路。从PID角度来看，其实就是一个系统校正。

极点（Poles）​​：​系统“惯性”与自然响应的根源。

物理本质​：极点由被控对象（加热管+测温系统）的物理特性决定，如热容、热阻、散热系数等。每个极点对应一个自然响应模式​（指数衰减或振荡）。

• 温度控制中的表现​：
  • ​实极点​（如 s = -1/τ）：代表热惯性，τ 是热时间常数。例如，加热管从冷态升温到目标温度需较长时间，对应缓慢的指数上升。
  • ​共轭复数极点​（如 s = -σ ± jω）：对应温度振荡。虚部 ω 是振荡频率（如加热-散热循环），实部 σ 是衰减速度（散热能力）。
• ​实际影响​：​极点位置越靠近虚轴（实部接近0）​，系统惯性越大，升温越慢，易振荡；远离虚轴（实部更负）​​ 则响应更快、更稳定。

​零点（Zeros）​​：​输入与输出的“耦合通道”特性​

• ​物理本质​：零点反映控制信号（PID输出）如何被系统“选择性放大或抑制”，体现控制器与对象的动态交互。
• ​温度控制中的表现​：
  • ​PID微分项（D）引入零点​：如 s = -K_p/K_d，增强对温度变化率的敏感性，抑制超调但放大噪声。
  • ​积分项（I）引入原点零点​：消除稳态误差，但可能引发低频振荡（如恒温区微小波动）。
• ​实际影响​：​左半平面零点加速响应但增加超调；右半平面零点可能破坏稳定性（如正反馈导致温度失控）。

PID是极点的“编辑工具”​​：通过调节参数重塑极点位置，实现从“缓慢无超调”到“快速无振荡”的任意平衡。

在PID温度控制系统中，正是通过传递函数对加热管控制系统建模，并通过调整PID参数来改变系统的动态响应特性，从而实现更精确的温度控制。

1.4 稳态误差

PID稳态误差：系统进入稳态时，实际值和目标值存在始终一个稳定的差值。

稳态误差产生原因：纯比例项控制时，若误差为0，则比例项结果也为0。被控对象输入0时，一般会自发地向一个方向偏移，产生误差。产生误差后，误差非0，比例项负反馈调控输出，当调控输出力度和自发偏移力度相同时，系统达到稳态。

判断是否会产生稳态误差：给被控对象输入0，判断被控对象会不会自发偏移。

判断稳态误差的方向：给被控对象输入0，自发偏移方向即为稳态误差方向。

针对稳态误差，如果只使用比例项控制，其实很容易理解，假设法如果目标值和实际值相同了，那么我们的输出值就是0，相当于是此时不给加热管开启或者电机PWM，这样就会导致系统自发的向一个方向偏移，例如电机速度降下来或者温度变低，此时又会产生误差，然后继续使用比例调节。
具体过程如下：

• 1、系统无误差，实际值和目标值相同，
• 2、误差为0，PID输出为0，加热管没有驱动力（电机没有驱动力）
• 3、腔体温度由于加热管没有启动，导致温度下降，产生误差。（电机由于摩擦力减速，产生误差）
• 4、误差越大，比例向输出越大，加热管开启时间越长。（电机驱动力越大，也就是PWM的占空比越长。）
• 5、加热管开启时间仅能保持腔体温度不会衰减，保持一个稳态，但是达不到我们想要的目标值。（电机驱动力与摩擦力平衡，电机不会减速误差不会增肌，驱动力不在增大，系统达到稳态。）
  对于电机定速控制来说，为什么会有稳态误差，原因就是电机有摩擦力。

基于腔体温度重新理解，

• 控制公式​：
  ΔD=Kp​⋅e(t)
  其中：
  • ΔD：占空比的调整量（如从 30% 调整到 40%，则 ΔD=10%）；
  • e(t)：当前误差（如目标温度 60°C，实际温度 55°C，则 e(t)=5°C）；
  • Kp​：比例增益（单位：​​%占空比/单位误差，例如 2%占空比/°C）。
• ​敏感度的体现​：
  • 若 Kp​=2%/°C，误差每增加 1°C → 占空比增加 2%；
  • 若 Kp​=0.5%/°C，相同误差下占空比仅增加 0.5%。
    ​​Kp​ 越大，相同误差触发的占空比调整幅度越大，系统对误差的“反应强度”越强。

假设加热管控温场景：

• ​目标温度​：60°C
• ​实际温度​：55°C → 误差 e(t)=5°C
• ​不同 Kp​ 下的占空比响应​：

Kp​ 值​	​占空比调整量 ΔD​​	​实际占空比变化​	​系统表现​
Kp​=0.5%/°C	ΔD=2.5%	从 30% → 32.5%	升温缓慢，可能无法快速消除误差
Kp​=2%/°C	ΔD=10%	从 30% → 40%	升温迅速，但可能超调振荡

• ​关键结论​：
  Kp​ 是误差到功率调整的转换系数，直接决定“误差需要多少控制动作来补偿”。

其实到这里，我们大概明白了Kp的具体实际意义，也就是一个敏感性的变量，用于在温度变化是否敏感。他只是一个转换系数，也就是我现在有温差，但是我怎么将温差的影响转换为实际加热管的开启时间，在这里我们强行的将这个关系定义为线性关系，是不是也是因为这个原因，才导致比例控制始终不用消除误差。

但是对误差还是没有深入理解。

稳态误差（Steady-State Error, ess​）在控制系统中的物理意义，本质上是系统为维持稳定运行所必须付出的“代价”，其产生源于能量动态平衡、系统结构限制及实际物理约束。

控制系统需持续对抗外部干扰（如散热、摩擦、负载变化），而比例控制（P控制）的输出与误差成正比，导致一个根本矛盾：

• ​零误差 → 零控制力​：若实际值完全等于目标值（e(t)=0），则控制输出 u(t)=Kp​⋅0=0，系统无法提供维持稳态所需的能量。

• ​需残余误差换取控制力​：系统需保留一个非零误差 ess​，使得控制输出 u=Kp​⋅ess​ 恰好抵消外部干扰，达到动态平衡。

怎么理解呐，通俗一点，我们在控制的时候是希望系统能保持一个状态一直运转，例如我们希望输出温度是60°，那么我们最终也希望系统维持60°的产生的能量。也就是持续输出，但是使用我们使用的是闭环控制，利用的还是比例控制根据其公式可以知道，如果没有误差，那么系统就不会进行主动的提供能量，这是我们比例控制公式本身的局限性已经控制本身就是依靠误差让系统动作。没有误差了那么系统就不会动作了。

因此系统就需要保持一个误差，但是该误差并不能理解为实际的误差，而是要从实际物理意义出发去理解这个误差。

就是我们将腔体的温度升到60°的过程加热管占空比是100%，但是当温度越来越高的时候我们加热管其实不需要100%占空比，又因为本身比例控制需要一个误差，那么这个误差其实就是腔体此时会自动散失能量，而我们这个时候设置散热管的占空比的目的就是补充温度的散失能量，也就是说最后的占空比一定是最少的，因为只需要维持散失的能量就行了。毕竟在开始的时候我们一方面要维持散失的能量，另一方面还要产生热量。

• 升温阶段（高误差 → 高占空比）​​
  • ​初始状态​：腔体温度远低于目标值（如目标60°C，实际20°C），误差 e(t) 极大。
  • ​控制响应​：比例控制器输出占空比 D=Kp​⋅e(t) 接近100%，加热管全功率工作，快速升温。
  • ​能量需求​：此时需同时补偿散热损耗​ + ​提升腔体蓄热，因此需高功率输入。
• ​过渡阶段（误差减小 → 占空比下降）​​
  • ​温度接近目标​：如实际温度升至58°C（误差2°C），占空比降至 D=Kp​×2（若 Kp​=10%/°C，则 D=20%)。
  • ​能量转换​：腔体蓄热需求减少，加热功率主要对抗持续散热​（如箱体导热、空气对流）。
• ​稳态阶段（残余误差 → 最小占空比）​​
  • ​平衡点建立​：实际温度稳定在58.5°C（静差1.5°C），此时占空比 D稳态​=Kp​×1.5 仅需提供恰好等于散热功率​ P损耗​ 的输出。
  • ​物理意义​：
    • 若误差为零（e(t)=0），则 D=0 → 加热管关闭 → 温度因散热下降；
    • 系统必须保留静差，以维持 D稳态​>0，确保最小加热功率补偿散热。

这个必须保留的静态误差，我觉得不是我们想保留，而是实际控制中产生出来的，或者说是使用这个控制器自洽出来的，也是一种能量守恒的必然结果。

在重新梳理一下，若误差为零（e(t)=0），则 D=0 → 加热管关闭 → 温度因散热下降；然后又会产生误差，进而又会让加热管工作。在这个过程中从能量的角度去理解，热量损失，加热管补充热量形成一个动态平衡。

在工程中，如果腔体不会散热，那就说明我们不需要控制了，因为腔体会一直保持温度60°，但是由于内部的结构或者食物需要消耗能量，那么这个60°的能量一直会被消耗，那就意味着我们需要一直的提供这个能量。

针对“由于内部的结构或者食物需要消耗能量”我们统一理解为能量的损耗，该控制系统需要让我们保持这个温度，那么在最后阶段我们的主要工作就是消除这个能量的损耗带来的影响。

从能量角度我们理解了这是控制系统在稳态以后能量守恒的结果。

1.5 解析稳态误差

但是从数学角度我们还是需要理解一下。

因为从我目前写到这里，我心中有一个疑问，就是系统为什么知道要这样？我还是无法将公式与能量角度对应上。

• 所有动态方程均源于守恒定律​（能量/质量），核心形式为：
  输入−输出=存储变化

在将数学意义与实际意义想互印证以及理解温度控制过程，首先我们应该站在全局的角度去考虑，而不是只考虑最终的问题状态。

对于整体的温控过程，我们的输入就是总的热量，减去输出的热量（也就是消耗的）等于最终的存储的。并且这个里面包含了两个公式。

一个是比例控制的器（控制方程）：

一个是系统的传递函数（系统模型）：

温度的滞后性需要注意。

我们可以看出在实际中其实是不知道系统的传递函数的，因为这是一个黑盒子，因此我们已知的能调节的就是P控制器。

但是我们在分析和理解的时候必须根据动态方程去理解，稳态误差到底是什么，到底怎么来的。

根据系统的传递函数，以及稳态方程我们知道：

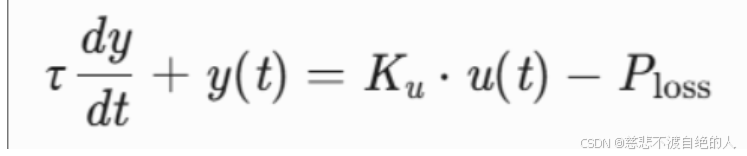
我们能控制的就是U(t),而U(t)又是怎么来的呐，是通过如下公式：

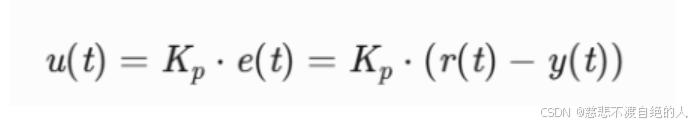
也就是我们的目标值减去实际值乘以该系统需要对温度变化的敏感性参数。

至此我们的系统方程与控制器产生了联系，并且是紧密的联系，那我们就接着分析稳态过程，通过系统的方程我们还可以知道：当前时刻的温度，其实还需要加上上一个时刻与这个时刻的变化量。因为上一时刻调节的温度具有滞后性。

这一点在使用机理法去推导最后的拉氏变换函数也证明了这一点。

经过对上述公式的分析，我们已经深入理解了这个公式。

那么我们现在需要考虑的稳态状态：

可以看出在使用比例控制的时候：稳态误差就是消耗的功率引起的，是系统自带的，是在现实世界中不管怎么都不能消除的，因为你不能消除系统的损耗功率。

那么就解决了我们疑问为什么会有系统误差，以及系统误差的来源。

系统误差，指的是系统控制的稳态误差。我们要做的就是怎么消除这个误差，或者说怎么降低这个系统控制的误差。

此时应该对这句话有了深刻理解。

---

文章源码获取方式：
如果您对本文的源码感兴趣，欢迎在评论区留下您的邮箱地址。我会在空闲时间整理相关代码，并通过邮件发送给您。由于个人时间有限，发送可能会有一定延迟，请您耐心等待。同时，建议您在评论时注明具体的需求或问题，以便我更好地为您提供针对性的帮助。

【版权声明】
本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议。这意味着您可以自由地共享（复制、分发）和改编（修改、转换）本文内容，但必须遵守以下条件：
署名：您必须注明原作者（即本文博主）的姓名，并提供指向原文的链接。
相同方式共享：如果您基于本文创作了新的内容，必须使用相同的 CC 4.0 BY-SA 协议进行发布。

感谢您的理解与支持！如果您有任何疑问或需要进一步协助，请随时在评论区留言。