力扣（LeetCode）第 459 场周赛

比赛链接： 第 459 场周赛

1. 判断整除性

题目内容

给你一个正整数 n。请判断 n 是否可以被以下两值之和 整除：

• n 的 数字和（即其各个位数之和）。

• n 的 数字积（即其各个位数之积）。

如果 n 能被该和整除，返回 true；否则，返回 false。

示例 1：

输入： n = 99

输出： true

解释：

因为 99 可以被其数字和 (9 + 9 = 18) 与数字积 (9 * 9 = 81) 之和 (18 + 81 = 99) 整除，因此输出为 true。

示例 2：

输入： n = 23

输出： false

解释：

因为 23 无法被其数字和 (2 + 3 = 5) 与数字积 (2 * 3 = 6) 之和 (5 + 6 = 11) 整除，因此输出为 false。

提示：

• 1 <= n <= 10^6

分析

根据题意计算，然后判断即可。

代码

class Solution {
public:bool checkDivisibility(int n) {int x=1,y=0;int t=n;while(t){int r=t%10;y+=r;x*=r;t/=10;}x+=y;if(n%x==0) return true;return false;}
};

2. 统计梯形的数目 I

题目内容

给你一个二维整数数组 points，其中 points[i] = [xi, yi] 表示第 i 个点在笛卡尔平面上的坐标。

水平梯形 是一种凸四边形，具有 至少一对 水平边（即平行于 x 轴的边）。两条直线平行当且仅当它们的斜率相同。

返回可以从 points 中任意选择四个不同点组成的 水平梯形 数量。

由于答案可能非常大，请返回结果对 10^9 + 7 取余数后的值。

示例 1：

输入： points = [[1,0],[2,0],[3,0],[2,2],[3,2]]

输出： 3

解释：

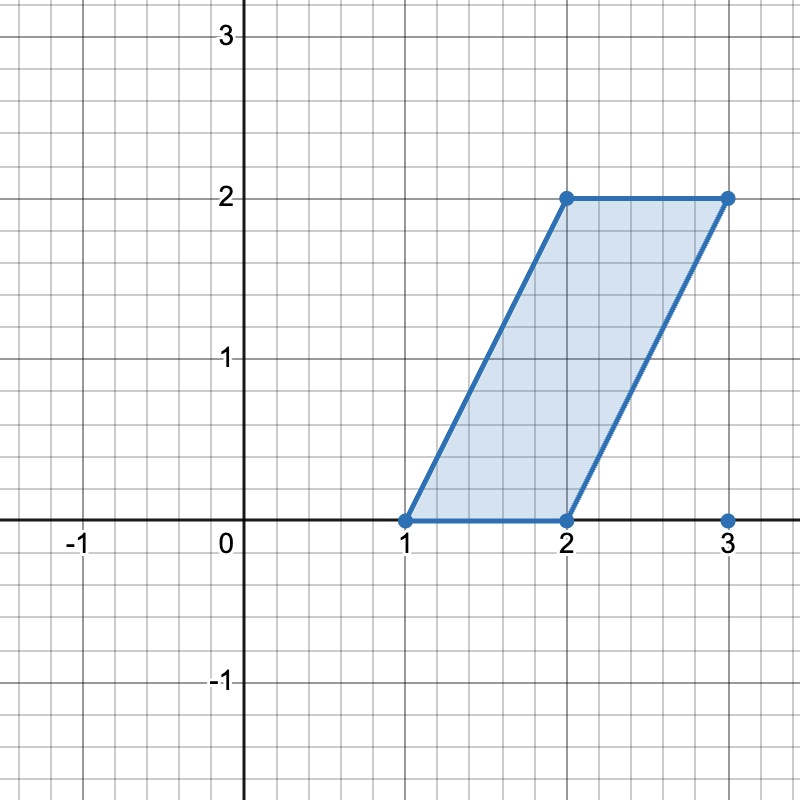
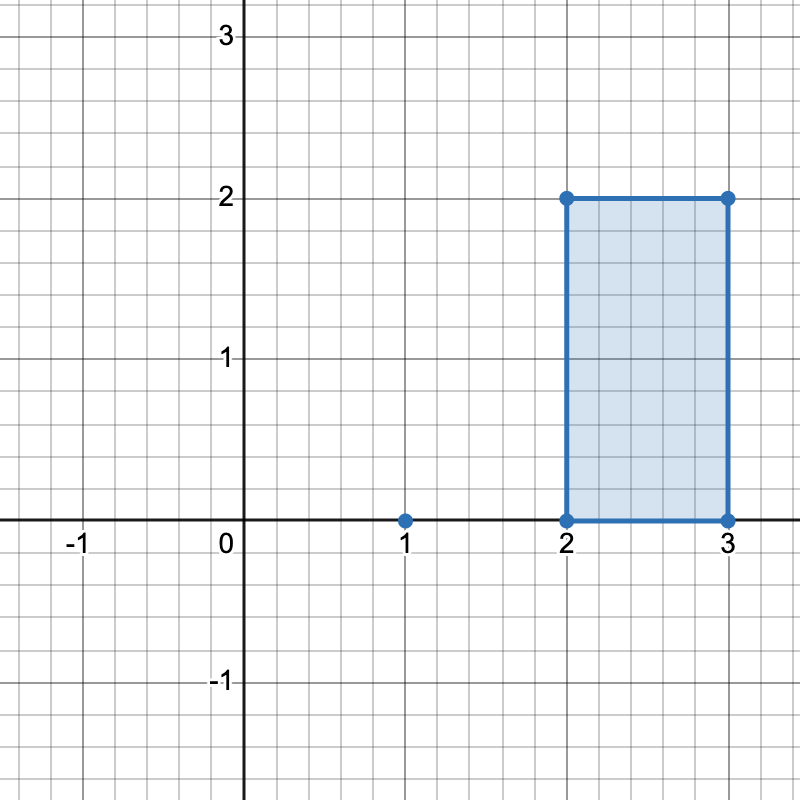
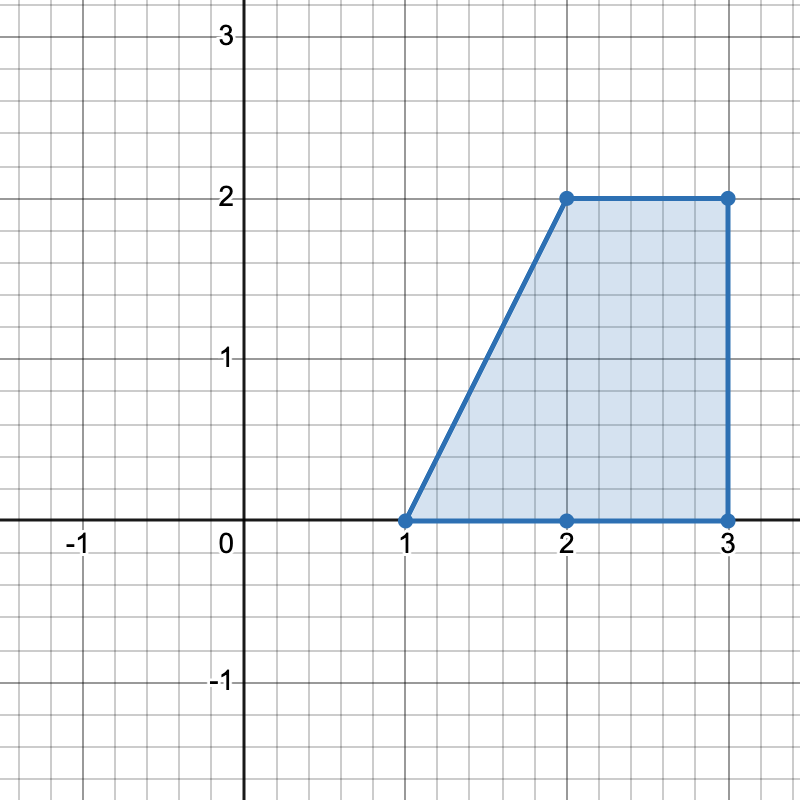
有三种不同方式选择四个点组成一个水平梯形：

• 使用点 [1,0]、[2,0]、[3,2] 和 [2,2]。
• 使用点 [2,0]、[3,0]、[3,2] 和 [2,2]。
• 使用点 [1,0]、[3,0]、[3,2] 和 [2,2]。

示例 2：

输入： points = [[0,0],[1,0],[0,1],[2,1]]

输出： 1

解释：

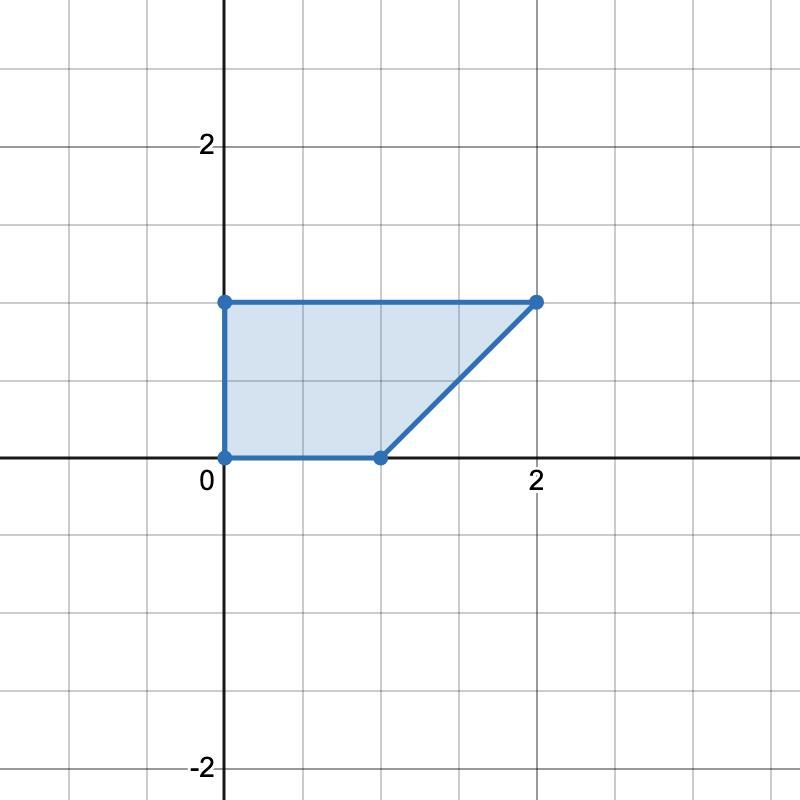
只有一种方式可以组成一个水平梯形。

提示：

• 4 <= points.length <= 10^5
• –10^8 <= xi, yi <= 10^8
• 所有点两两不同。

分析

题目要求水平梯形，两个点连线与x轴平行即两点y坐标相同。
用map记录所有不同y的点数有多少个。
枚举每一个y，设这一行的水平边$c=cnt\ast (cnt-1)/2$，那么另外一条水平边就是之前遍历过的y的水平边数$s$
那么就有$c\ast s$个梯形，加入答案。

代码

class Solution {public:    int countTrapezoids(vector<vector<int>>& g) {int n=g.size();map<int,int> mp;for(auto it:g){int x=it[0],y=it[1];mp[y]++;}const int mod=1e9+7;long long s=0,ans=0;for(auto [y,cnt]:mp){long long c=1ll*cnt*(cnt-1)/2%mod;ans=(ans+s*c)%mod;s=(s+c)%mod;}return ans;}
};

3. 位计数深度为 K 的整数数目 II

题目内容

给你一个整数数组 nums。

对于任意正整数 x，定义以下序列：

• p0 = x
• pi+1 = popcount(pi)，对于所有 i >= 0，其中 popcount(y) 表示整数 y 的二进制表示中 1 的个数。

这个序列最终会收敛到值 1。

popcount-depth（位计数深度）定义为满足 pd = 1 的最小整数 d >= 0。

例如，当 x = 7（二进制表示为 "111"）时，该序列为：7 → 3 → 2 → 1，因此 7 的 popcount-depth 为 3。

此外，给定一个二维整数数组 queries，其中每个 queries[i] 可以是以下两种类型之一：

• [1, l, r, k] - 计算在区间 [l, r] 中，满足 nums[j] 的 popcount-depth 等于 k 的索引 j 的数量。
• [2, idx, val] - 将 nums[idx] 更新为 val。

返回一个整数数组 answer，其中 answer[i] 表示第 i 个类型为 [1, l, r, k] 的查询的结果。

示例 1：

输入： nums = [2,4], queries = [[1,0,1,1],[2,1,1],[1,0,1,0]]

输出： [2,1]

解释：

i	queries[i]	nums	binary(nums)	popcount- depth	[l, r]	k	有效 nums[j]	更新后的 nums	答案
0	[1,0,1,1]	[2,4]	[10, 100]	[1, 1]	[0, 1]	1	[0, 1]	—	2
1	[2,1,1]	[2,4]	[10, 100]	[1, 1]	—	—	—	[2,1]	—
2	[1,0,1,0]	[2,1]	[10, 1]	[1, 0]	[0, 1]	0	[1]	—	1

因此，最终 answer 为 [2, 1]。

示例 2：

输入： nums = [3,5,6], queries = [[1,0,2,2],[2,1,4],[1,1,2,1],[1,0,1,0]]

输出：[3,1,0]

解释：

i	queries[i]	nums	binary(nums)	popcount- depth	[l, r]	k	有效 nums[j]	更新后的 nums	答案
0	[1,0,2,2]	[3, 5, 6]	[11, 101, 110]	[2, 2, 2]	[0, 2]	2	[0, 1, 2]	—	3
1	[2,1,4]	[3, 5, 6]	[11, 101, 110]	[2, 2, 2]	—	—	—	[3, 4, 6]	—
2	[1,1,2,1]	[3, 4, 6]	[11, 100, 110]	[2, 1, 2]	[1, 2]	1	[1]	—	1
3	[1,0,1,0]	[3, 4, 6]	[11, 100, 110]	[2, 1, 2]	[0, 1]	0	[]	—	0

因此，最终 answer 为 [3, 1, 0] 。

示例 3：

输入： nums = [1,2], queries = [[1,0,1,1],[2,0,3],[1,0,0,1],[1,0,0,2]]

输出：[1,0,1]

解释：

i	queries[i]	nums	binary(nums)	popcount- depth	[l, r]	k	有效 nums[j]	更新后的 nums	答案
0	[1,0,1,1]	[1, 2]	[1, 10]	[0, 1]	[0, 1]	1	[1]	—	1
1	[2,0,3]	[1, 2]	[1, 10]	[0, 1]	—	—	—	[3, 2]
2	[1,0,0,1]	[3, 2]	[11, 10]	[2, 1]	[0, 0]	1	[]	—	0
3	[1,0,0,2]	[3, 2]	[11, 10]	[2, 1]	[0, 0]	2	[0]	—	1

因此，最终 answer 为 [1, 0, 1] 。

提示：

• 1 <= n == nums.length <= 10^5
• 1 <= nums[i] <= 10^15
• 1 <= queries.length <= 10^5
• queries[i].length == 3 或 4
  • queries[i] == [1, l, r, k] 或
  • queries[i] == [2, idx, val]
  • 0 <= l <= r <= n - 1
  • 0 <= k <= 5
  • 0 <= idx <= n - 1
  • 1 <= val <= 10^15

分析

注意k的范围很小，我们可以开6（k<=5）个树状数组维护每个深度，单点修改，区间修改。
注意：求整数二进制表示1的个数时，不要使用__builtin_popcount去求，这个只能求unsigned int范围内的，而题目给的整数会超过此范围。

代码

class Solution {
public:vector<int> popcountDepth(vector<long long>& a, vector<vector<long long>>& q) {int n=a.size();vector<vector<int>> tr(8,vector<int>(n+1,0));auto lowbit=[&](int x)->int{return x&(-x);};auto add=[&](vector<int> &vec,int x,int v)->void{for(;x<=n;x+=lowbit(x)) vec[x]+=v;};auto c=[&](long long x)->int{int cnt=0;while(x){int r=x%2;if(r==1) cnt++;x/=2;}return cnt;};auto cal=[&](long long x)->int{int cnt=0;while(x!=1){x=c(x);cnt++;}return cnt;};auto ask=[&](vector<int> &vec,int x)->int{int res=0;for(;x;x-=lowbit(x)) res+=vec[x];return res;};for(int i=0;i<n;i++){int cnt=cal(a[i]);add(tr[cnt],i+1,1);// cout<<cnt<<'\n';}vector<int> ans;for(int i=0;i<q.size();i++){vector<long long> qu=q[i];if(qu.size()==3){long long op=qu[0],id=qu[1],val=qu[2];id++;int pre=cal(a[id-1]);int now=cal(val);add(tr[pre],id,-1);add(tr[now],id,1);a[id-1]=val;}else{long long op=qu[0],l=qu[1],r=qu[2],k=qu[3];l++,r++;ans.push_back(max(0,ask(tr[k],r)-(l!=0?ask(tr[k],l-1):0)));}}return ans;}
};

4. 统计梯形的数目 II

题目内容

给你一个二维整数数组 points，其中 points[i] = [xi, yi] 表示第 i 个点在笛卡尔平面上的坐标。

返回可以从 points 中任意选择四个不同点组成的梯形的数量。

梯形 是一种凸四边形，具有 至少一对 平行边。两条直线平行当且仅当它们的斜率相同。

示例 1：

输入： points = [[-3,2],[3,0],[2,3],[3,2],[2,-3]]

输出： 2

解释：

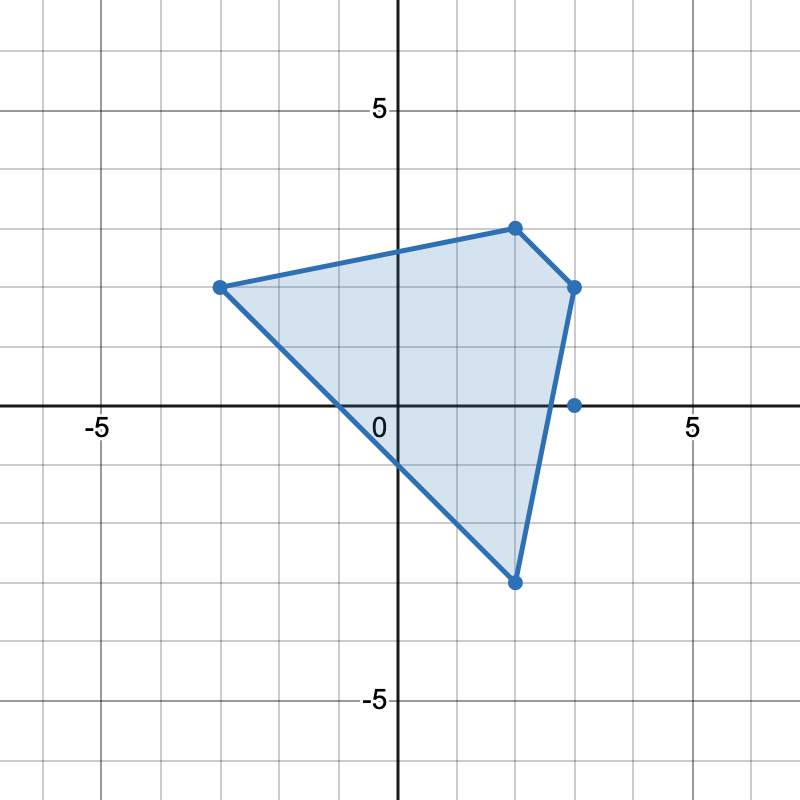
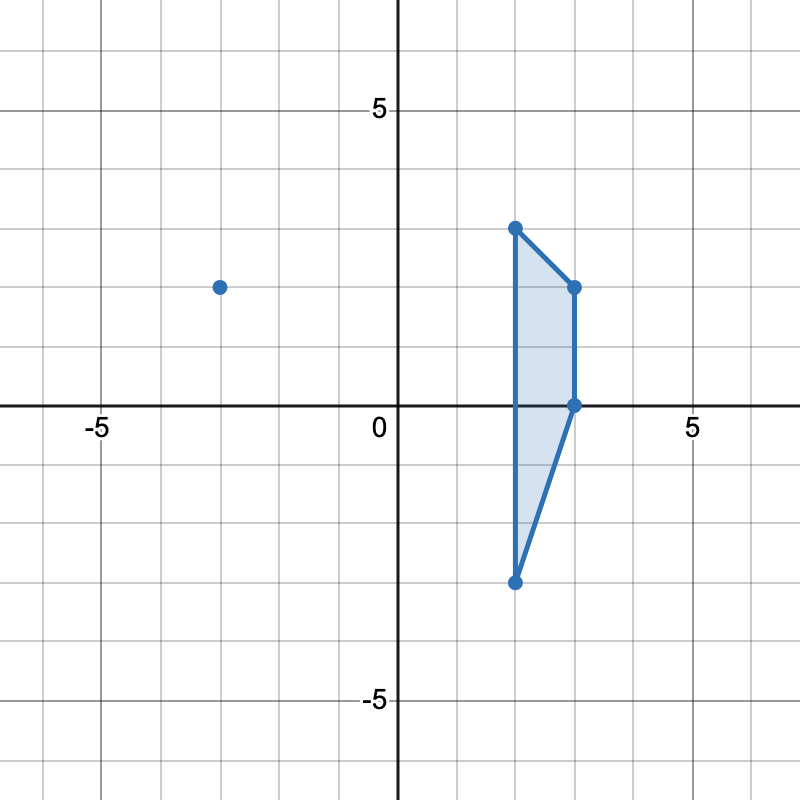
有两种不同方式选择四个点组成一个梯形：

• 点 [-3,2], [2,3], [3,2], [2,-3] 组成一个梯形。
• 点 [2,3], [3,2], [3,0], [2,-3] 组成另一个梯形。

示例 2：

输入： points = [[0,0],[1,0],[0,1],[2,1]]

输出： 1

解释：

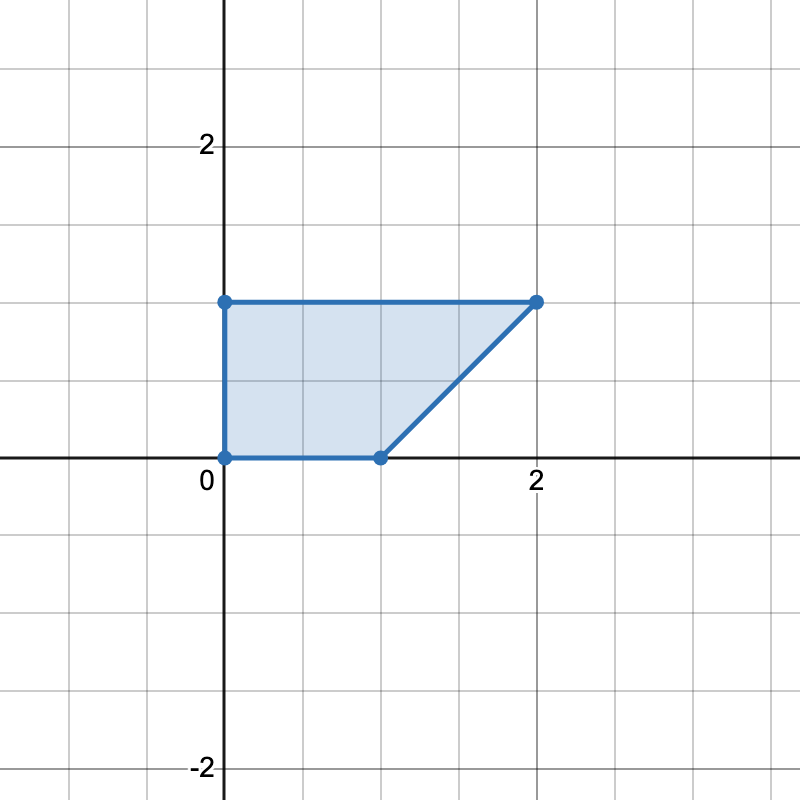
只有一种方式可以组成一个梯形。

提示：

• 4 <= points.length <= 500
• –1000 <= xi, yi <= 1000
• 所有点两两不同。

分析

因为题目n范围<=500，我们n^2求出所有直线，用map记录所有斜率相同的，因为我们不能选择两条重合的直线，所以需要再套一个map记录所有截距。我记为map1
但是这样会导致平行四边形重复计算，我们需要删掉这些重复计算的，考虑到平行四边形的性质有一个是对角线的交点相同，即中位数相同，我们用map记录所有中位数，但由于我们不能选择两条重合的边，所以还要再套一个map对斜率进行分组。我记为map2
总体思路就是：计算所有直线+去掉重复计算的平行四边形。

代码

class Solution {
public:int countTrapezoids(vector<vector<int>>& p) {map<double,map<double,int>> mp1;map<pair<int,int>,map<double,int>> mp2;int n=p.size();for(int i=0;i<n;i++){int x1=p[i][0],y1=p[i][1];for(int j=0;j<i;j++){int x2=p[j][0],y2=p[j][1];double dx=x2-x1;double dy=y2-y1;double k=dx?1.0*dy/dx:DBL_MAX;double b=dx?1.0*(y1*dx-x1*dy)/dx:x1;mp1[k][b]++;mp2[{x1+x2,y1+y2}][k]++;}}int ans=0;for(auto [it,x]:mp1){int s=0;for(auto [it1,y]:x){ans+=s*y;s+=y;}}for(auto [it,x]:mp2){int s=0;for(auto [it1,y]:x){ans-=s*y;s+=y;}}return ans;}
};