数列-冒泡排序,鸡尾酒排序
冒泡排序
排序思想(向前冒泡):
- 一次只排好一个数,针对n个数,最差情况需要n-1次就可以排好,最好情况需要0次(交换位置)
- 每次排序假定第一个元素是最大或最小的,然后相邻的两个元素依次进行比较,遇到较大或较小的元素进行交换,访问完数组的最后一个元素,就排好了一个数。
- 在余下的元素中,再次应用第2步操作,直到只剩下1个数。
推理:
例如:将5,4,3,2,1冒泡排序为1,2,3,4,5
排序演示:
第0轮:5,4,3,2,1 → 4,3,2,1,5 比较4次 = 数组长度5 - 轮数0 - 1
第1轮:4,3,2,1,5 → 3,2,1,4,5 比较3次 = 数组长度5 - 轮数1 - 1
第2轮:3,2,1,4,5 → 2,1,3,4,5 比较2次 = 数组长度5 - 轮数2 - 1
第3轮:2,1,3,4,5 → 1,2,3,4,5 比较1次 = 数组长度5 - 轮数3 - 1
总结:
-
案例涉及到5个数的排序,排序了4轮,得到:轮数 = 元素个数(数组大小)- 1,我们可以通过一个外层for循环实现轮数的遍历。
-
案例涉及的每一轮中数列的排序次数,得到:次数 = 元素个数 - 轮数 [- 1],我们可以通过一个内层for循环实现每一轮次数的遍历。
-
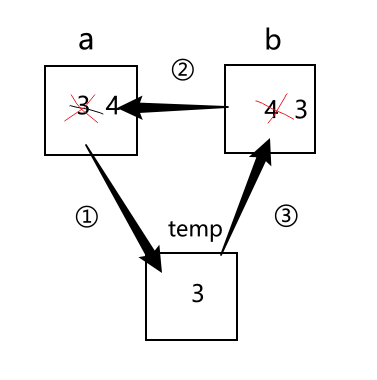
每一次比较过程中,两个数涉及到位置交换,比如 a = 3, b = 4,交换ab的数据变为 a = 4,b = 3,应该如何实现:
-
引入一个临时变量temp,将a的值赋值给temp,int temp = a;
-
将b的值赋值给a, a = b;
-
将temp的值赋值给b, b = temp;
-
代码
#include <stdio.h>int main(int argc,char *argv[])
{// 创建一个数组,用来存放冒泡排序的数列int arr[10];// 定义循环变量和临时变量、是否升序排序,默认降序int i,j,temp,desc = 1;printf("请输入10个整数:\n");// 计算数组的大小int len = sizeof(arr) / sizeof(arr[0]);// 通过控制台依次录入10个数字for (i = 0; i < len; i++) scanf("%d", &arr[i]);// &arr[i]:[]的优先级高于&,[]跟arr结合,获取数组中的某个元素,再跟&结合,对这个元素取地址printf("\n排序前:");for (i = 0; i < len; i++) printf("%-4d", arr[i]);printf("\n");// 冒泡排序// 外层循环:实现排序轮数的遍历:轮数 = 数组大小 - 1for (i = 0; i < len - 1; i++){// 设置一个flag,用来判断数组是否已经有序int flag = 0;// 内层循环:实现每一轮的比较次数:比较次数 = 数组大小 - 本轮轮数 - 1for (j = 0; j < len - i -1; j++){// 相邻的两个数比较后,如果满足交换条件,就要交换位置// 降序排序: if(arr[j] < arr[j+1])// 升序排序: if(arr[j] > arr[j+1])if (desc){// 降序if(arr[j] < arr[j+1]){temp = arr[j];arr[j] = arr[j+1];arr[j+1] = temp;flag = 1;}}else{// 升序if(arr[j] > arr[j+1]){temp = arr[j];arr[j] = arr[j+1];arr[j+1] = temp;flag = 1;}}}if (!flag) break; // 如果进行了1轮之后flag还是等于0,则说明排序数列已经有序,后续轮数不再继续}printf("\n排序后:");for (i = 0; i < len; i++) printf("%-4d", arr[i]);printf("\n");return 0;
}结果示例:

衍生
冒泡排序 → 鸡尾酒排序、摇坠排序、摇床排序、搅拌排序…
鸡尾酒排序
代码
#include <stdio.h>int main(int argc, char *argv[]) {int arr[10];int i, j, temp, desc = 1; // desc=1表示降序,0表示升序int len = sizeof(arr) / sizeof(arr[0]);printf("请输入10个整数:\n");for (i = 0; i < len; i++) scanf("%d", &arr[i]);printf("\n排序前:");for (i = 0; i < len; i++) printf("%-4d", arr[i]);// 鸡尾酒排序核心实现int start = 0;int end = len - 1;int swapped = 1;while (swapped) {swapped = 0;// 正向遍历:将最大值移动到end位置for (j = start; j < end; j++) {if (desc) { // 降序排序if (arr[j] < arr[j+1]) {temp = arr[j];arr[j] = arr[j+1];arr[j+1] = temp;swapped = 1;}} else { // 升序排序if (arr[j] > arr[j+1]) {temp = arr[j];arr[j] = arr[j+1];arr[j+1] = temp;swapped = 1;}}}end--; // 最大值已就位,缩小右边界// 反向遍历:将最小值移动到start位置for (j = end - 1; j >= start; j--) {if (desc) { // 降序排序if (arr[j] < arr[j-1]) {temp = arr[j];arr[j] = arr[j-1];arr[j-1] = temp;swapped = 1;}} else { // 升序排序if (arr[j] > arr[j-1]) {temp = arr[j];arr[j] = arr[j-1];arr[j-1] = temp;swapped = 1;}}}start++; // 最小值已就位,扩大左边界}printf("\n排序后:");for (i = 0; i < len; i++) printf("%-4d", arr[i]);printf("\n");return 0;
}
示例运行效果
请输入10个整数:
5 8 6 3 9 2 7 1 4 10排序前: 5 8 6 3 9 2 7 1 4 10
排序后: 10 9 8 7 6 5 4 3 2 1 (降序)
关键改进说明
-
双向遍历机制:
- 正向遍历:从左到右将当前最大值移动到末尾(
end位置),每轮结束后end--缩小右边界。 - 反向遍历:从右到左将当前最小值移动到开头(
start位置),每轮结束后start++扩大左边界。 - 这种双向移动使得每轮排序可以同时确定最大值和最小值的位置,减少总轮数。
- 正向遍历:从左到右将当前最大值移动到末尾(
-
动态边界调整:
start和end变量动态标记无序区间的左右边界。- 例如:第一轮排序后,最大值在
end位置,最小值在start位置,后续排序只需处理[start, end]区间。
-
提前终止条件:
swapped标志位记录本轮是否发生交换。- 若某轮双向遍历后未发生交换(
swapped=0),说明数组已完全有序,直接终止排序。
-
排序方向控制:
-
desc变量控制排序方向:
desc=1时降序(默认):正向比较arr[j] < arr[j+1],反向比较arr[j] < arr[j-1]。desc=0时升序:正向比较arr[j] > arr[j+1],反向比较arr[j] > arr[j-1]。
-
与冒泡排序的对比优势
| 特性 | 冒泡排序 | 鸡尾酒排序 |
|---|---|---|
| 遍历方向 | 单向(左→右) | 双向(左→右 + 右→左) |
| 平均轮数 | O(n) | O(n/2) |
| 提前终止条件 | 单方向无交换 | 双向均无交换 |
| 最优时间复杂度 | O(n) | O(n) |
| 适用场景 | 完全无序数据 | 部分有序数据 |
注意事项
- 鸡尾酒排序在数据接近有序时效率显著提升,但最坏时间复杂度仍为 O (n²),不适合大规模数据。
- 代码中
start和end的初始值分别为 0 和len-1,每次遍历后动态调整。 - 反向遍历时
j的取值范围是[end-1, start],避免重复比较已排序区域。
