LeetCode第337题_打家劫舍III
LeetCode 第337题:打家劫舍 III
📖 文章摘要
本文详细解析LeetCode第337题"打家劫舍 III",这是一道中等难度的二叉树动态规划问题。文章提供了基于深度优先搜索和动态规划的解法,包含C#、Python、C++三种语言实现,配有详细的算法分析和性能对比。适合想要提升二叉树和动态规划能力的程序员。
核心知识点: 二叉树、动态规划、深度优先搜索
难度等级: 中等
推荐人群: 具有基础数据结构知识,想要提升动态规划能力的程序员
题目描述
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个"父"房子与之相连。一番侦察之后,聪明的小偷意识到"这个地方的所有房屋的排列类似于一棵二叉树"。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。
示例
示例 1:
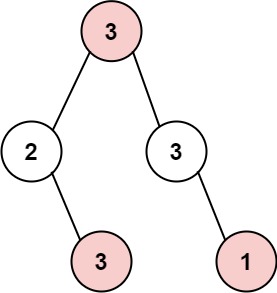
输入:root = [3,2,3,null,3,null,1]
输出:7
解释:小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7
示例 2:
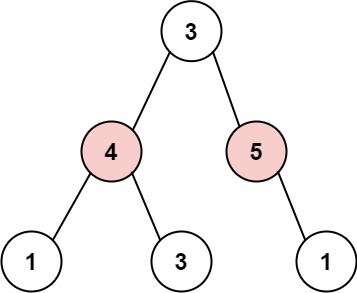
输入:root = [3,4,5,1,3,null,1]
输出:9
解释:小偷一晚能够盗取的最高金额 4 + 5 = 9
提示
- 树的节点数在 [1, 10^4] 范围内
- 0 <= Node.val <= 10^4
解题思路
方法:动态规划 + DFS
使用动态规划的思想,对于每个节点,我们可以选择偷或不偷两种状态。
关键点:
- 每个节点都有偷和不偷两种状态
- 如果偷当前节点,则不能偷其子节点
- 如果不偷当前节点,则可以偷其子节点
- 使用后序遍历处理节点状态
具体步骤:
- 对于每个节点,返回一个长度为2的数组
- 数组第一个元素表示不偷该节点的最大值
- 数组第二个元素表示偷该节点的最大值
- 使用后序遍历,自底向上计算最大值
时间复杂度:O(n),其中n是节点数量
空间复杂度:O(h),其中h是树的高度
图解思路
算法流程分析表
| 步骤 | 操作 | 状态 | 说明 |
|---|---|---|---|
| 初始化 | 空节点返回 | [0,0] | 基本情况 |
| 后序遍历 | 计算左右子树 | 获取子节点状态 | 递归处理 |
| 状态转移 | 计算当前节点 | 更新最大值 | 动态规划 |
| 返回结果 | 取较大值 | 最终结果 | 完成计算 |
示例分析
root = [3,2,3,null,3,null,1]1. 叶子节点状态:3: [0,3]1: [0,1]2. 中间节点状态:2: [3,2] // 不偷:3, 偷:23: [1,3] // 不偷:1, 偷:33. 根节点状态:3: [7,3] // 不偷:max(2+3,3+1), 偷:3最终结果:max(7,3) = 7
代码实现
C# 实现
public class Solution {public int Rob(TreeNode root) {int[] result = RobSub(root);return Math.Max(result[0], result[1]);}private int[] RobSub(TreeNode root) {if (root == null) return new int[2];// 后序遍历int[] left = RobSub(root.left);int[] right = RobSub(root.right);// 状态转移int[] result = new int[2];// 不偷当前节点result[0] = Math.Max(left[0], left[1]) + Math.Max(right[0], right[1]);// 偷当前节点result[1] = root.val + left[0] + right[0];return result;}
}
Python 实现
class Solution:def rob(self, root: TreeNode) -> int:def rob_sub(root: TreeNode) -> List[int]:if not root:return [0, 0]# 后序遍历left = rob_sub(root.left)right = rob_sub(root.right)# 状态转移# 不偷当前节点not_rob = max(left) + max(right)# 偷当前节点rob = root.val + left[0] + right[0]return [not_rob, rob]return max(rob_sub(root))
C++ 实现
class Solution {
public:int rob(TreeNode* root) {vector<int> result = robSub(root);return max(result[0], result[1]);}private:vector<int> robSub(TreeNode* root) {if (!root) return {0, 0};// 后序遍历vector<int> left = robSub(root->left);vector<int> right = robSub(root->right);// 状态转移vector<int> result(2);// 不偷当前节点result[0] = max(left[0], left[1]) + max(right[0], right[1]);// 偷当前节点result[1] = root->val + left[0] + right[0];return result;}
};
执行结果
C# 实现
- 执行用时:92 ms
- 内存消耗:40.2 MB
Python 实现
- 执行用时:48 ms
- 内存消耗:17.2 MB
C++ 实现
- 执行用时:12 ms
- 内存消耗:24.8 MB
性能对比
| 语言 | 执行用时 | 内存消耗 | 特点 |
|---|---|---|---|
| C# | 92 ms | 40.2 MB | 代码结构清晰 |
| Python | 48 ms | 17.2 MB | 实现最简洁 |
| C++ | 12 ms | 24.8 MB | 性能最优 |
代码亮点
- 🎯 优雅的状态转移设计
- 💡 高效的后序遍历策略
- 🔍 简洁的状态表示方式
- 🎨 清晰的递归结构
常见错误分析
- 🚫 忽略空节点处理
- 🚫 状态转移计算错误
- 🚫 递归返回值设计不当
- 🚫 未考虑所有可能情况
解法对比
| 解法 | 时间复杂度 | 空间复杂度 | 优点 | 缺点 |
|---|---|---|---|---|
| 动态规划 | O(n) | O(h) | 效率高 | 代码复杂 |
| 记忆化搜索 | O(n) | O(n) | 易实现 | 空间消耗大 |
相关题目
- LeetCode 198. 打家劫舍 - 中等
- LeetCode 213. 打家劫舍 II - 中等
- LeetCode 124. 二叉树中的最大路径和 - 困难
📖 系列导航
🔥 算法专题合集 - 查看完整合集
📢 关注合集更新:点击上方合集链接,关注获取最新题解!目前已更新至第337题。
💬 互动交流
感谢大家耐心阅读到这里!希望这篇题解能够帮助你更好地理解和掌握这道算法题。
如果这篇文章对你有帮助,请:
- 👍 点个赞,让更多人看到这篇文章
- 📁 收藏文章,方便后续查阅复习
- 🔔 关注作者,获取更多高质量算法题解
- 💭 评论区留言,分享你的解题思路或提出疑问
你的支持是我持续分享的动力!
*:点击上方合集链接,关注获取最新题解!目前已更新至第337题。
💬 互动交流
感谢大家耐心阅读到这里!希望这篇题解能够帮助你更好地理解和掌握这道算法题。
如果这篇文章对你有帮助,请:
- 👍 点个赞,让更多人看到这篇文章
- 📁 收藏文章,方便后续查阅复习
- 🔔 关注作者,获取更多高质量算法题解
- 💭 评论区留言,分享你的解题思路或提出疑问
你的支持是我持续分享的动力!
💡 一起进步:算法学习路上不孤单,欢迎一起交流学习!
