伊吖学C笔记（6、数、求和、排列）

一、数

1.自然数、奇偶数

自然数也就是非负整数，C的循环语句很容易输出自然数，比如：输出100以内的自然数。

奇数、偶数也都是自然数：

2. 约数、因数

题目：一个数如果恰好等于它的因子之和，这个数就称为“完数”。例如6=1＋2＋3.编程找出1000以内的所有完数。

约数是指两个‌自然数之间，如果一个数能被另一个数整除（不包括0），那么这个数就是另一个数的约数。例如，1、2、4、8、16都是16的约数，因为16可以被这些数整除。

整数n的因数是一个非零整数m，使得m乘上某个整数后可以得到n，此时也称n是m的一个倍数。因数范围大一些，可以负：3的因数有1，-1，3，-3。

因子是不包含本身的因数。6的因子有1、2、3。

完数，即完全数（Perfect number），是一些特殊的自然数，它所有的真因子（即除了自身以外的约数）的和恰好等于它本身‌。

如何找出一个整数的各因数呢？思路：C一般通过%余数是否为0来判断两数是否整除，只有整除，除数才是被除数的因数。要找出一个整数的所有因数，我们加入一个循环，把比它小的数都除一遍，比如找出30的所有因数：

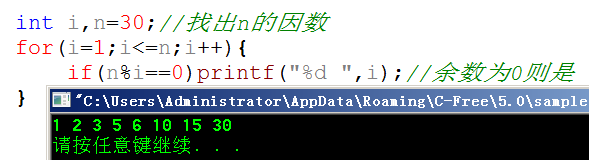
此题，不需要本身这个最大因数，所以呢，只循环到一半就可以了，即循环到n/2=15，如下：

用“n/2”代替“n”，可以减少循环次数，提高效率。

接下来，我们加入真因子求和的语句：

判断完数?将所求之和与原数比较，是否相等？如下：

要找出1000以内的所有完数，我们在外层再加层循环，从2循环到999，如下：

外循环每次求和s要清零。习惯i外层j内层。

题目：将一个正整数分解质因数。例如：输入90,打印出90=2*3*3*5。

思路：和上面的差不多，通过%判断能否整除，从2开始循环，到n/2结束。不同的是，如果找到出了一个因子，比如90%2=0，即90=2*45，这时就要把45当作被除数，再开始从2循环；2不行再3，3可以，得45=3*15；此时要把15当作被除数，再从2开始...直到最后的5没有因子。也就是说，循环体的条件是变化的，当找到一个因子时，i的起止范围要重新设置。

我们先用90来调试一下主循环部分：

分别用其他几个数运行下：

主体没有问题，我们把程序补充完整。

题目：输入两个正整数m和n，求其最大公约数和最小公倍数。

最大公约数怎么求？上学时老师是这么教的：

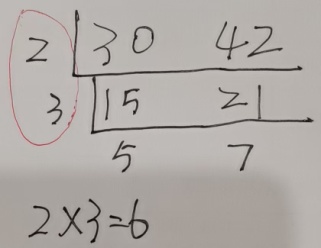
可以想到，通过前面的分解质因数，分别求两个数的质因数，然后再找出相同的乘起来，就是最大公约数。但是这个方法编程太复杂（两组数比较，还有重复数）。

同样的思路，我们也可以把两个数的所有因数全求出来，比如30的因数有（1、2、3、5、6、15、30），42的因数有（1、2、3、6、7、14、21、42），然后再比较找出相同的最大数6。这个方法编程还是太复杂，有无更简单的方法呢？

当然有。下面介绍3种方法。

①穷举法。

又叫暴力遍历，流程图为：

就是利用计算机处理快的特点，从其中一个数开始，把它当作临时除数，分别去除原两个数，如果同时除尽了，就是最大公约数，除不尽，就把临时除数减1，再分别去除...直到除尽。上例，先用30去除30、42，一个除不尽，再用29，再用28...直到6，同时除尽，即6为最大公约数。举例代码如下：

上面5行代码虽然实现了求最大公约数，但效率是很不高的。如果前面是大数（比如a=3000,b=42），那循环的次数是从3000到42都是不必要的，所以在循环前，把a、b比较一下，小的放a上，这样效率高些。改进后的代码如下：

这种方法思路简单清晰，只是执行效率较低。

②辗转相除法（辗除法）

两个整数的最大公因数等于其中较小的数和两数相除余数的最大公因数。

按照上面的说法，大数除以小数，把较小数和余数（比较小数更小，假设为余1号），重新当作两个整数，循环定义，这两个数的最大公因数等于余1号和余2号（原较小的数除以余1号所得余数）的公因数...如此循环等于，直到最后两个数除尽。

如何理解？例题1，我们把b=8当作一把尺子，去量a的长度，正好3尺，余0，所以8就是最大公约数。

（除尽才是公约数）

例题2，把28当作尺子去量35，1尺余7。这时公约数变成了28与7的公约数了。再把7当尺子去量28，正好4尺，余0，7就是最大公约数。

可以看出，两数相除有余数，那公约数一定小于等于这个余数。流程图为：

程序设计：显然这个循环次数不可知，只知道停止条件，用for不好使，条件在前面，用while来实现。先调试一下：

这段代码中，要不要比较a、b的大小呢？不需要。如果较小数除以较大数，余数为较小数，置b，较大数赋给a，一次循环完成互换。

最小公倍数如何求？记住这个公式：

a*b=最小公倍数*最大公约数

先求最大公约数，再算最小公倍数。

该题目加上最小公倍数后的完整代码如下：

如果两个数互质，最大公约数为1。

辗除法虽然理解有点绕，但循环次数少，效率高。

③辗转相减法（更相减损法）。

这种方法的原理与辗除法相通，理解为“对剪”：谁长剪谁，每次剪去以短为尺的长度，直到两者相等。下面以10和6为例，图示过程：

程序设计流程如下：

这种方法，如果两个数相差很大的话，比如30与30000，要减很多次，效率较低。实现代码如下：

综合上述3种方法，辗除法更为可取。

3.质数（素数）

‌题目：判断101-200之间有多少个素数，并输出所有素数。

素数（质数）‌：在大于1的自然数中，除了1和此整数自身外，无法被其他自然数整除的数‌。

有了前面求约数的思路，我们也可通过循环遍历，判断一个数是不是素数。

最原始的想法：从2到它本身小1，一个个去除，如果都除不尽（余数都不为0），那它就是素数。这个想法当然不错，虽然粗暴但目的明确、不管效率。

如果我们想一想，有必要把这些数都过一遍吗？经过前面的“n/2”操作，很显然不必要。一个数求约数时，只需要循环到“n/2”，因为大于“n/2”是肯定除不尽的。

比如找100的约数，只需要用2-50去试除100即可，51-99是一定不能整除100的。

所以有了：for(i=2;i<=n/2;i++)，提高了不少效率。

我们再想想，在判断一个有没有除了1和本身的其它约数时，一定要循环到“n/2”吗？还有没有减少循环次数的可能？答案是可以的。一个数的约数都是成对的，比如100有（2*50）（4*25）（10*10），我们循环到10就可以了，10-50之间也没有必要去循环了。

也就是说：一个数从2到它的平方根都除不尽的话，那它就是质数。所以我们可以这样设定循环：

for(i=2;i*i<=n;i++)，用“i*i<=n”放入循环条件中，代替sqrt()函数，使程序看起来整洁美观。调试如下：

基本结构可以这样，不是素数的判断写好了，但如果是素数，循环完了还要判断一下，怎么弄呢？

方法1：我们可以把循环条件“i*i<=n”反置成“(i+1)*(i+1)>n”，提前判断循环是否结束，如果大于n，下一个循环一定是不会进行的。代码如下：

这样虽然可行，但降低了效率，每次循环都计算并判断一次，虽然结构清晰但不是太可取。

方法2：最简单的方法就是在循环体外加个标识，初置为1，如有整除置0，循环结束后重新判断一次，如下：

一个数的判断写好了，我们再在外层加个101-200的主循环，双层循环体结构，如下：

方法3：对素数的判断是一个固定的功能，我们可以把它定义为一个函数，主循环直接调用函数的结果，这样的程序结构思路更清晰，块状化设计更美观，相对于多层循环，更好理解更好阅读。如下：

虽然两种方式都是8句，显然后一种更一目了然。

题目：一个偶数总能表示为两个素数之和。

前面没有把2、3考虑进去，在定义判断是否为素数的函数时，要加上一句if(a==2||a==3)return 1;

二、数列求和

1、求和

规则的数列，比如等差、等比数列，有求和公式可以直接使用。但在程序设计中，循环法是更好的选择。

题目：有一分数序列：2/1，3/2，5/3，8/5，13/8，21/13...求出这个数列的前20项之和。

思路：无论多复杂的数列，只要前后两项变化规律是一致的就好办。观察发现：后一项分母总是前一项分子，后一项分子总是前一项（分子+分母）之和。

这中间要设个t，作为临时中转用，就象两个值互换时多设一个临时变量t一样。

题目：编写一个函数，输入n为偶数时，调用函数求1/2+1/4+...+1/n,当输入n为奇数时，调用函数1/1+1/3+...+1/n。

这个有两种可能性，分支结构，分别定义两个函数，结构清晰，如下：

在循环设计时，我们把通常i++变为i+=2，将步进由1改为2，更符合变化的通项，减少了程序设计的复杂度。

题目：求1+2!+3!+...+20!的和。

显然，主体用一个1到20的循环，循环中调用一个阶乘函数（我们可以用递归函数），如下：

2.收敛等比数列“和”的极值

等比数列如果|q|<1,就属收敛型，它的和会趋于一个极值。

再换几个试试：

三、排列组合

题目：有1、2、3、4个数字，能组成多少个互不相同且无重复数字的三位数？都是多少？

思路：首先排第一个位子，有4种选择，再排第二个位子有3种，最后第三个位子有2种。我们用一层循环i来排百位，用第二层循环j来排十位，但要加个条件：j！=i；用第三层循环k来排个位，也要加条件：k!=i&&k!=j，既不能等于i也不能等于j。代码如下：

题目：求0—7所能组成的奇数个数。

思路：此题，奇数显然是以1、3、5、7为结尾的数，题目意思从1位奇数到8位奇数全部统计出来。先从简单思考：1位奇数：4个；2位奇数：个位数4种可能，十位数6种可能（0不排首），4*6=24；3位奇数：个位4种可能，百位6种可能，十位6种（0加入），4*6*6=144；...8位奇数：4*6*6*5*4*3*2*1=17280。我们可以设定主循环为从1到8位奇数，循环里加入判断和连乘。如下：

题目：约瑟夫环。有n个人围成一圈，顺序排号。从第一个人开始报数（从1到3报数），凡报到3的人退出圈子，问最后留下的是原来第几号的那位。

思路：这是约瑟夫环问题。有n个人，每个人都有唯一的编号，首先考虑到用数组把每个编号存进去；围成一圈，没有首尾，意思是在数到最后一个后，自动跳到数组的第一个。在数组里，索引环形跳动可用index=(index+1)%n实现；指针呢，就要加一个判断p!=a+n-1，不是最后就p++，否则就回头p=a。报数报到3就退出，我们需要设置一个报数变量k，当k=3时，把对应的数组值置0，*p=0，就好象报到3就把灯灭了，循环进行，最后一个亮着的灯就是答案。由于不知道循环次数，用while来解决，到底循环多少次退出呢？也就是退出条件如何设定呢？我们把每灭一次灯计个数，如果这个数等于n-1了，就退出。while循环的主体框架如下：

while（退出条件）｛

if（条件）先做什么（报1、2，记下来）

if（条件）再做什么（报3，数组置0，读数器置0，统计+1）

转圈（指针向下移或数组索引加1）

｝

调试代码如下：

在指针跳变前，分别输出数组当前的值，清楚内部的变化，看是不是按我们预想的在转圈。完整代码如下：

通过自定义函数，解决数组定义问题，直接返回最后一个数。

也可以不用指针，用数组索引解决，部分代码如下：

我们再来看看Python代码：

python列表（相当对C的数组）具有删除的方法，长度自动减1，处理起来更简洁。C没有这个功能，但可以模拟实现，代码如下：

题目：猴子分桃。海滩上有一堆桃子，五只猴子来分。第一只猴子把这堆桃子凭据分为五份，多了一个，这只猴子把多的一个扔入海中，拿走了一份。第二只猴子把剩下的桃子又平均分成五份，又多了一个，它同样把多的一个扔入海中，拿走了一份，第三、第四、第五只猴子都是这样做的，问海滩上原来最少有多少个桃子？

思路：每次的变化都是一样，那就好办。可以从前往后，假设为x，第一次x-1整除5余0，取5份中的4份，循环中可写成：x=(x-1)/5*4，循环5次，看是否能整除？然后加个大的循环遍历x，5次都能整除就是要找的数。代码如下：

我们也可从后往前，最后猴子分得i个桃，那前一个就是i*5/4+1，循环体内写成x=x*5/4+1，同样内循环5次，遍历i从1开始。代码如下：

还找几个数看看：