【论文阅读32】预期寿命预测（2024）

论文聚焦于滑坡寿命（滑坡失效时间）的动态预测，针对经典预测模型（Verhulst模型、GM(1,1)模型和Saito模型）在动态条件下表现不足的问题，提出了一种基于机器学习（ML）的集成系统，**通过将多个经典模型的预测结果作为输入，**利用机器学习算法（尤其是决策树回归器DTR）构建元模型，实现对滑坡寿命的更准确预测。

[1] Liu L L, Yin H D, Xiao T, et al. Dynamic prediction of landslide life expectancy using ensemble system incorporating classical prediction models and machine learning[J]. Geoscience Frontiers, 2024, 15(2): 101758.

论文的主要贡献和结论包括：

1. 经典预测模型表现有限：单独使用Verhulst、GM(1,1)、Saito模型对滑坡寿命进行动态预测时，准确度和预测质量较低，且存在较多无效预测。

2. 集成模型提升预测性能：将多个经典模型集成在机器学习框架下，显著提高了预测的准确性和可靠性，减小了单模型带来的误差，特别是在滑坡预警的关键阶段（橙色和红色预警）表现更优。

3. 决策树回归器（DTR）作为元模型的优势：在多种机器学习算法中，DTR最适合构建集成系统的元模型，能够有效处理小样本和低相关性输入变量，且其预测更稳定，避免极端误差。

4. 解释性分析：利用SHAP方法分析了各经典模型对最终集成预测结果的贡献，发现Verhulst和Saito模型对预测值有较大正向影响，GM(1,1)贡献较小。

5. 局限与未来展望：目前研究样本量较小，未采用深度学习模型，未来可以尝试利用大数据条件下的深度学习方法和超参数优化技术，进一步提升集成系统预测性能。

总结来说，论文提出了一种基于机器学习的滑坡寿命动态预测集成框架，有效提升了传统经典模型的预测能力，为滑坡灾害预警和风险管理提供了更可靠的技术手段。

---

摘要

随着滑坡监测系统的发展，基于位移监测数据预测滑坡失稳时间的研究已得到广泛关注。诸如 Verhulst 模型、GM(1,1) 模型和 Saito 模型等经典预测方法，依据滑坡位移特性判定失稳时间，已被大量研究与应用。在实际监测过程中，监测工作是持续进行的，监测数据集不断更新，这意味着滑坡寿命预测值（即每个预测时刻预测失稳时间与当前时刻之间的滞后时间）也应随时间动态修正，这种方式被称为“动态预测”。然而，现有研究尚未探讨经典模型在动态预测条件下的表现。

本研究首先对经典模型在动态预测中的性能进行了评估，并基于四个实际滑坡的监测数据，指出了各经典模型在应用中的不足。随后，本文提出了一种更优的集成模型，将多种经典模型通过机器学习（ML）元模型进行集成。为评价各模型在动态预测下的性能，提出了一项新指标——“失信指数（β）”，β 值越高表示预测质量越差。结果表明，Verhulst 模型与 Saito 模型在预测中产生的 β 值显著偏高，而 GM(1,1) 模型的平均绝对误差（MAE）最大。相比之下，集成模型的预测精度与适用性均优于单一经典模型，其中基于决策树回归（decision tree regression）的集成模型表现最佳。

---

1. 引言

滑坡灾害可能导致严重的经济损失和人员伤亡（Gu 等, 2023）。为了减轻滑坡带来的危害，通常会布设监测系统（Baum and Godt, 2010；Zhang 等, 2018；Rodriguez 等, 2021；Lau 等, 2023）。滑坡位移及其导数（如速度与加速度）相关的监测数据被认为是预测滑坡发生最可靠的指标（Intrieri 等, 2019）。在滑坡风险评估领域，如何高效利用监测数据及时发出预警信号始终是一个充满挑战的问题（Chae 等, 2017；Segalini 等, 2018；Fan 等, 2019）。尤其随着实时滑坡监测技术的发展，大量与滑坡位移相关的数据可以通过全球导航卫星系统（GNSS）等传感器实时获取，数据更新频率也显著提高。进入大数据时代（Zhang 等, 2021c）后，亟需开发更加高效可靠的预测模型用于滑坡失稳时间预测，并构建适用于实时数据更新环境下的预测模型评价方法。

为了预测滑坡发生时间，传统方法通常依据滑坡位移在失稳前明显加速阶段（即三级蠕变阶段）的几何特性外推失稳时间。例如，Saito（1969）提出了基于三级蠕变曲线的典型经验模型（Saito 模型），根据土体在三级蠕变阶段的变形速率经验规律预测滑坡失稳时间。此外，还常采用通过求解微分方程拟合三级蠕变曲线形态的方法预测滑坡失稳时间。例如，Verhulst 模型（Li 等, 1996；Li 等, 2021）与 GM(1,1) 模型（Wang, 2017）均基于回归理论，通过在回归函数中引入经验常数，建立滑坡位移与时间的关系。在此基础上，通常以预测位移达到某一失稳阈值或无穷大值作为滑坡失稳时间判据（Zhou, 2012；Wang, 2017；Huang 等, 2021；Li 等, 2021）。总体来看，经典预测方法多基于加速蠕变理论，属于经验型或半经验型方法，因此在特定工况和样本数据下表现良好，但存在一定偏倚性（Intrieri 等, 2019）。换言之，当样本数据发生变化时，原本表现优异的经典预测模型可能无法维持预测性能。因此，在实时滑坡监测系统中，随着数据池的持续更新，单一经典预测模型的性能难以得到保障。

由于经典预测方法为工程师所熟知，并被广泛应用于工程实践，因此有必要探索在实时滑坡监测数据动态变化条件下提升经典模型预测精度和预测质量的方法。此外，尽管经典预测方法已被岩土工程界广泛使用，但目前尚未有研究在动态监测位移背景下系统性地评价这些方法的预测性能（Carlà 等, 2017；Zhou 等, 2020）。在实际工程应用中，滑坡监测通常持续至失稳发生，监测数据不断上传，实时刷新数据池。因此，每次开展预测时，滑坡寿命预测值（$T\_fp-t\_p$，即预测失稳时间 $T\_fp$ 与当前预测时刻 $t\_p$ 之间的滞后时间）也应随监测数据的更新而重新评估。这意味着滑坡寿命预测工作需基于更新数据持续开展，即预测工作在整个监测过程中具有动态性，本文将其称为“动态预测”。

在动态预测情形下，单一精度指标（如平均绝对误差 MAE）难以全面评价预测方法的性能，因为滑坡寿命预测结果会随时间不断刷新。目前尚无研究系统性探讨预测方法在动态预测背景下的适用性，部分原因在于缺乏合理的评价指标。基于此，本文的主要创新与贡献在于：(1) 探讨经典预测方法在监测数据动态变化条件下预测滑坡失稳时间的性能；(2) 提出一种适用于动态预测场景、预测质量更优的高级方法。

为此，本文引入了“失信指数”（$\beta$），该指标表示预测结果处于失信区间的比例。基于失信指数，本文系统评价了三种经典预测模型（即 Verhulst、GM(1,1) 和 Saito 模型）在滑坡寿命动态预测中的表现。随后，借鉴机器学习（ML）领域的 stacking 集成系统理念（Kardani 等, 2021），开发了一种更优的方法，旨在克服单一经典预测模型性能不足的问题。stacking 集成系统通过构建元模型，将多种机器学习算法融合，从而实现更高的预测精度。在构建该集成系统过程中，本文采用前馈神经网络（FNN）、支持向量机（SVR）和决策树回归（DTR）三种机器学习算法分别作为元模型，并对不同算法的预测性能进行比较。接下来的章节将综述并探讨机器学习技术及集成系统在自然灾害预测中的应用现状。

2. 前人研究

在过去的几十年里，随着人工智能（AI）技术的发展，时间序列分析、机器学习（ML）与深度学习（DL）方法已被应用于滑坡预测领域（Ma 等，2017；Miao 等，2018；Zhang 等，2021a；Zeng 等，2022）。在早期阶段，经典的机器学习算法（如支持向量回归（SVR）与决策树回归（DTR））被用于滑坡预测（Lian 等，2014；Zhou 等，2016；Miao 等，2018）。例如，Li 和 Kong（2014）利用 SVR 预测受周期性降雨和水库水位波动影响的滑坡位移。Liu 等（2014）对比了 SVR、相关向量机（RVM）和遗传编程（GP）在滑坡位移预测中的表现。Ma 等（2017）提出了一种基于 DTR 的混合算法，用于预测受降雨和水库水位上升诱发的滑坡位移。为将不确定性纳入滑坡预测，Zhang 等（2022）提出了一种基于贝叶斯的机器学习算法，用于滑坡破坏时间预测。

近年来，深度学习算法被频繁应用于滑坡预测研究中。例如，Guo 等（2020）结合时间序列分析与反向传播神经网络（BPNN），建立滑坡位移预测公式。为考虑滑坡演化过程的动态特性，Zeng 等（2022）采用长短期记忆网络（LSTM）进行滑坡位移预测。尽管深度学习方法通常被认为较传统机器学习方法具有更强的预测能力，但在建立 DL 模型时通常需要较大规模的样本数据（Nguyen 和 Kim，2021）。在部分小样本数据情形下，机器学习方法在滑坡预测中甚至可能优于深度学习方法（Saha 等，2021）。

可解释人工智能（XAI）的兴起为滑坡灾害研究提供了一种有力工具，可以实现模型构建决策过程的可视化。例如，Al-Najjar 等（2023）使用 SHAP（Shapley Additive Explanation）方法解释滑坡易发性评价中 ML 模型的建模决策过程，可评估模型构建中各因素间的交互作用与相关性。Ge 等（2023）采用 SHAP 技术直观解释各输入因素对滑坡位移预测结果的影响。Pradhan 等（2023a）将卷积神经网络（CNN）与 SHAP 算法结合应用于滑坡易发性建模，发现 SHAP 算法在特征选择与空间影响性检验方面具备优势。

除滑坡灾害研究外，XAI 技术也被应用于水文气象灾害评价中。例如，Dikshit 和 Pradhan（2021）基于 XAI 框架，解释数据驱动预测模型在不同干旱条件与时间尺度下的标准化降水指数（SPI）预测结果，报道了影响因子对干旱预测中气候变量的重要性。Pradhan 等（2023b）利用 SHAP 算法分析洪水敏感性制图中的影响因子，指出 XAI 技术在提升 AI 算法洪水敏感性制图可解释性方面的优势。Abdollahi 和 Pradhan（2023）应用 SHAP 分析方法，探讨野火敏感性预测结果中的影响因素，并指出量化各影响因子对野火敏感性评估结果的贡献，有助于野火灾害的防控。

总体而言，AI 算法在预测能力上通常优于传统预测方法。然而，某一 AI 算法在某一训练数据集上表现良好，并不能保证在另一数据集或监测数据动态更新情形下具备同样优异的泛化能力（Kardani 等，2021）。因此，单一 AI 预测模型的预测精度在面对不同滑坡案例或动态变化的监测数据环境下同样难以保证。

为克服单一 AI 算法预测性能不稳定的问题，集成学习系统（ensemble system）被广泛采用（Kardani 等，2021；Pham 等，2021；Towfiqul Islam 等，2021；Abdollahizad 等，2023）。Towfiqul Islam 等（2021）在洪水易发性建模中提出了基于 dagging 和随机子空间算法构建的集成模型，发现集成模型的预测能力优于单个模型。Kardani 等（2021）提出了一种 stacking 集成算法用于边坡稳定性预测，将多个单体 ML 算法通过元模型集成，结果表明集成模型的预测结果优于单体 ML 模型。

Abdollahizad 等（2023）对比了多种单体 ML 模型与集成模型在滑坡易发性分析中的预测性能，发现集成模型较单体模型具备更强的鲁棒性，因其在模型训练过程中产生的误差可在集成系统内得到修正。此外，研究还指出 stacking 集成系统通常优于 voting 集成系统。

在本研究中，采用 stacking 集成系统框架，旨在提升经典预测模型（即 Verhulst、GM（1,1）与 Saito 模型）在动态预测环境下的预测精度与质量。在 stacking 集成系统框架下，将上述经典模型与 ML 元算法（即 FNN、SVR 和 DTR）集成，具体方法见前文所述。

3. 研究区

本研究选取了4个滑坡案例，分布于中国甘肃、湖南、山西和贵州4个省份（即中国中西部地区），如图1所示。从这4个滑坡案例中共采集了11条监测时间序列，这些数据由GNSS传感器或裂缝计获取（见图2）。以下小节将对4个滑坡案例及其相应的数据来源进行详细介绍。

3.1 黑方台滑坡

黑方台地区位于黄河上游的河流阶地，面积约13.7 km²。在滑坡发生前，研究区南侧存在一处高差约120–160 m的边坡，主要由第四纪黄土组成，边坡基岩则主要为砂质泥岩。2017年8月，该地区变形显著加剧，并于2017年10月1日凌晨5点发生了滑坡（即黑方台滑坡）。黑方台滑坡的位置及滑坡迹地如图1b所示。同时，图2a展示了通过布设于滑坡主裂缘上的裂缝计（见图1b）在2017年5月至10月期间所监测到的累计位移，监测频率为每日一次。从图2a中可观察到，2017年10月以前，累计位移整体呈稳定增长趋势，并在2017年10月6日前后出现了显著增长。

3.2 雷家山滑坡

雷家山滑坡位于湖南省常德市石门县。该滑坡体上下部陡峭，中部相对平缓，滑坡体长度约500 m，宽度约300 m，主要由第四纪残积含砾粉质粘土组成，基岩则主要为泥灰岩和含碳页岩。为了监测该地区位移，布设了8个GNSS监测站点，如图1c所示。与此同时，图2b展示了2020年4月至7月期间，通过GNSS监测站点测得的累计位移监测数据。从图2b可见，监测初期位移较为稳定，并于2020年6月下旬开始呈上升趋势。受7月4日至6日连续强降雨影响，边坡位移显著增加，滑坡最终于2020年7月6日下午5点发生。需要注意的是，在图2b中，某些时段监测到的累计位移存在负值。这种监测数据异常波动的可能原因是环境因素对传感器的干扰，如天气、气温、车辆震动和人为活动等（Carlà et al., 2017；Fan et al., 2019）。

3.3 卧龙寺滑坡

卧龙寺滑坡位于山西省宝鸡市金台区，是一处浅层黄土滑坡，发生时间为1971年5月5日凌晨3点。该滑坡原始边坡高差约为559.9–732.5 m，区域上部地层主要为第四纪松散堆积物，下伏为砾石及粘土。如图1d所示，滑坡边界呈椭圆形，南北长约645 m，东西宽约650 m。本研究采用了1971年3月11日至5月5日期间，通过布设于滑坡主裂缘处的裂缝计（见图1d）测得的累计位移数据（见图2c），用于数据平滑及模型构建。从图2c可观察到，累计位移量总体处于0–70 mm的较小范围内，说明该滑坡破坏过程呈脆性特征。此外，可以看出在1971年5月以前，累计位移缓慢稳定增长，而1971年5月2日后位移量迅速增大。

3.4 龙井村滑坡

龙井村滑坡位于贵州省兴义市西南部，发生时间为2019年2月17日。该滑坡为岩质滑坡，滑体体积约132万 m³，主要由三叠系白云岩、泥质白云岩和石灰岩组成。原始边坡上部陡峭，下部较缓，总体呈“舌状”形态。龙井村滑坡前缘陡壁基本呈垂直状态，底部岩层裸露。本研究采用了2019年1月27日至2月16日期间，通过布设于滑坡主裂缘处的裂缝计（见图1e）测得的累计位移数据（见图2d），用于数据平滑及模型构建。从图2d可以观察到，2019年2月12日前累计位移总体平稳增长，而在2019年2月18日出现了突增，滑坡最终于2019年2月19日发生。

---

4. 方法论

4.1. 滑坡位移监测数据的预处理

在建立预测模型之前，应对滑坡位移监测数据进行预处理。首先，应对监测数据进行平滑处理，以消除由测量误差及其他外部因素（如车辆引起的振动）造成的噪声影响。其次，应提取并采用与土体三次蠕变阶段相关的数据建立模型，该阶段表示滑坡位移显著加速（见图3）。数据平滑方法及三次蠕变阶段的判定方法将在以下小节中详细讨论。

4.1.1. 数据平滑

平滑方法常用于消除原始样本数据中的噪声影响，常见方法包括移动平均法（Du等，2013）、双指数平滑法（Huang等，2017）和多项式平滑法（Xu和Niu，2018）。由于移动平均法原理简单，计算效率高且准确性较好，因此被广泛用于滑坡位移时间序列的平滑处理（Carlà等，2017；Miao等，2018；Fan等，2019；Li等，2021）。本研究采用移动平均法，其计算公式为：

$$S_i=\frac{S_{i-\frac{N}{2}}+\cdots +S_{i-1}+S_i+S_{i+1}+\cdots +S_{i+\frac{N}{2}}}{N}\text{\hspace{1em}(1)}$$

其中，$S\_i$ 表示第 $i$ 个时刻的累计位移，$N$ 表示移动平均的阶数，由监测周期的时间尺度决定。根据文献，$N$ 通常取 3 到 7 之间（Carlà等，2017），本研究取 $N=7$。

4.1.2. 土体三次蠕变阶段的判定

滑坡演化过程通常包括三个蠕变阶段：初次蠕变、二次蠕变和三次蠕变（见图3）。初次蠕变阶段开始时变形速率较大，随后趋于稳定且变形速率较小；二次蠕变阶段在重力作用下，变形速率相对恒定，变形曲线一般为直线；三次蠕变阶段变形速率逐渐加快，直至滑坡破坏，亦称加速蠕变阶段。在滑坡破坏时间预测中，通常选取三次蠕变阶段的监测位移数据作为样本（Rose和Hungr，2007；Mufundirwa等，2010；Manconi和Giordan，2016；Qi等，2020；Zhou等，2020；Li等，2021）。因此，应基于第4.1.1节中获得的平滑数据（Intrieri等，2019）判定三次蠕变阶段。本研究采用切线角量化法（Xu等，2011）判定三次蠕变阶段。

通过累计位移 $S$ 除以土体运动速度 $v$，使 $S$ 和时间 $t$ 具有相同维度。在切线角量化法中，通常考虑土体整体运动的平均速度 $v\_i$，其表达式为：

$$v_i=\frac{S_i}{t_i}\text{\hspace{1em}(2)}$$

其中，$t\_i$ 表示第 $i$ 个监测时刻。然后，将累计位移 $S$ 转换为相对监测时间的垂直坐标 $T\_i$，计算公式为：

$$T_i=\frac{S_i}{v_i}\text{\hspace{1em}(3)}$$

由此，$T\_i$ 与 $t$ 的曲线的切线角 $a\_i$ 计算为：

$$a_i=\arctan \frac{T_i-T_{i-1}}{t_i-t_{i-1}}\text{\hspace{1em}(4)}$$

根据上述公式，当 $a\_i=45^{\circ }$ 时，表示土体处于二次蠕变阶段（即速度恒定）；而 $a\_i>45^{\circ }$ 时，提取的数据即为三次蠕变阶段的数据。

4.2. 经典预测模型

本研究首先实现了Saito模型、Verhulst模型和GM (1,1)模型，用于滑坡破坏时间预测。随后，在集成系统框架下对这些模型进行融合，以提升预测精度和质量。为适应动态监测数据集，模型采用基于监测周期频率的动态输入样本（见图3）。如图所示，动态输入样本包含从三次蠕变阶段起始点至当前监测周期末的累计位移数据。滑坡破坏时间的预测结果随时间动态更新，实现动态预测。样本数据为每个传感器经过第4.1节预处理后的历史位移监测数据。以下介绍经典模型的基本概念及公式。

4.2.1. Saito模型

Saito模型由日本学者Saito提出（Saito，1969）。模型选取三次蠕变阶段位移-时间曲线上对应于时间点 $t\_1$, $t\_2$, $t\_3$ 的三个节点，且要求位移满足 $t\_2-t\_1$ 与 $t\_3-t\_2$ 之间的位移相等。滑坡破坏时间预测公式为：

$$T_{fp}=t_1+\frac{1}{2}\frac{(t_2-t_1{)}^2}{(t_2-t_1)-\frac{1}{2}(t_3-t_1)}\text{\hspace{1em}(5)}$$

4.2.2. Verhulst模型

Verhulst模型由德国生物学家Verhulst于1937年提出，原用于预测生物繁殖随时间的演变。滑坡演化过程包含三个阶段：恒速变形（二次蠕变）、加速变形（三次蠕变）和变形终止（破坏），对应生物繁殖的接种、发展和死亡阶段。因此，Verhulst模型常用于滑坡破坏时间预测（Li等，1996；Miao等，2017；Li等，2021）。Verhulst模型的灰色微分方程为：

$$\frac{dx}{dt}=ax-b{x}^2\text{\hspace{1em}(6)}$$

其中，$a$ 和 $b$ 为白化系数。考虑等距监测，滑坡位移时间序列 $x^0$ 表示为：

$$x^0=(x^0(1),x^0(2),\dots ,x^0(n-1),x^0(n))\text{\hspace{1em}(7)}$$

通过累加生成新序列 $x^1$：

$$x^1=(x^1(1),x^1(2),\dots ,x^1(n-1),x^1(n))\text{\hspace{1em}(8)}$$

其中，

$$x^1(k)=\sum _{i=1}^k{x}^0(i)$$

利用最小二乘法计算 $a$ 和 $b$：

$$\left(\begin{array}{c}a\\ b\end{array}\right)=(B^{T}B{)}^{-1}{B}^{T}Y\text{\hspace{1em}(9)}$$

矩阵 $B$ 和向量 $Y$ 表示为：

$$B=\left(\begin{array}{cc}{Z}^1(t_2)& -[Z^1(t_2){]}^2\\ Z^1(t_3)& -[Z^1(t_3){]}^2\\ ⋮& ⋮\\ Z^1(t_k)& -[Z^1(t_k){]}^2\end{array}\right),k=2,3,\dots ,n\text{\hspace{1em}(10)}$$

$$Z^1(t_k)=\frac{1}{2}[x^1(t_k)+x^1(t_{k-1})],k=2,3,\dots ,n\text{\hspace{1em}(11)}$$

$$Y=\left(\begin{array}{c}{x}^0(t_2)\\ x^0(t_3)\\ ⋮\\ x^0(t_n)\end{array}\right)\text{\hspace{1em}(12)}$$

解该灰色微分方程，得到位移随时间演化的表达式：

$$x^1(t)=\frac{a{x}^1(t_1)}{b{x}^1(t_1)+(a-b{x}^1(t_1))e^{a(t-t_1)}}\text{\hspace{1em}(13)}$$

当速度达到最大值，位移满足 $x^1=\frac{a}{2b}$，将其代入式（13），可求得滑坡预测破坏时间为：

$$T_{fp}=\frac{1}{a}\ln \left(\frac{b{x}^1(t_1)}{a-b{x}^1(t_1)}\right)+t_1\text{\hspace{1em}(14)}$$

4.2.3. GM (1,1)模型

GM (1,1)模型是基于灰色系统理论的典型模型（Liu和Yang，2011）。通过对原始时间序列累加生成的新序列可近似为一阶线性微分方程，适用于三次蠕变阶段的演化预测，因此在滑坡破坏时间预测中被广泛应用（Wang，2017；Huang等，2021）。GM (1,1)模型的灰色微分方程为：

$$\frac{dx}{dt}=ax+b\text{\hspace{1em}(15)}$$

其中，$a$ 和 $b$ 为白化系数。计算系数方法与Verhulst模型类似，不同的是矩阵 $B$ 表达为：

$$B=\left(\begin{array}{cc}{Z}^1(t_2)& 1\\ Z^1(t_3)& 1\\ ⋮& ⋮\\ Z^1(t_k)& 1\end{array}\right),k=2,3,\dots ,n\text{\hspace{1em}(16)}$$

位移随时间的演化公式为：

$$x^1(k)=\left(x^0(1)-\frac{b}{a}\right)e^{-a(k-1)}+\frac{b}{a},k=2,3,\dots$$

4.5 本研究的实施流程

图6展示了本研究的实施流程图，主要包含以下步骤：

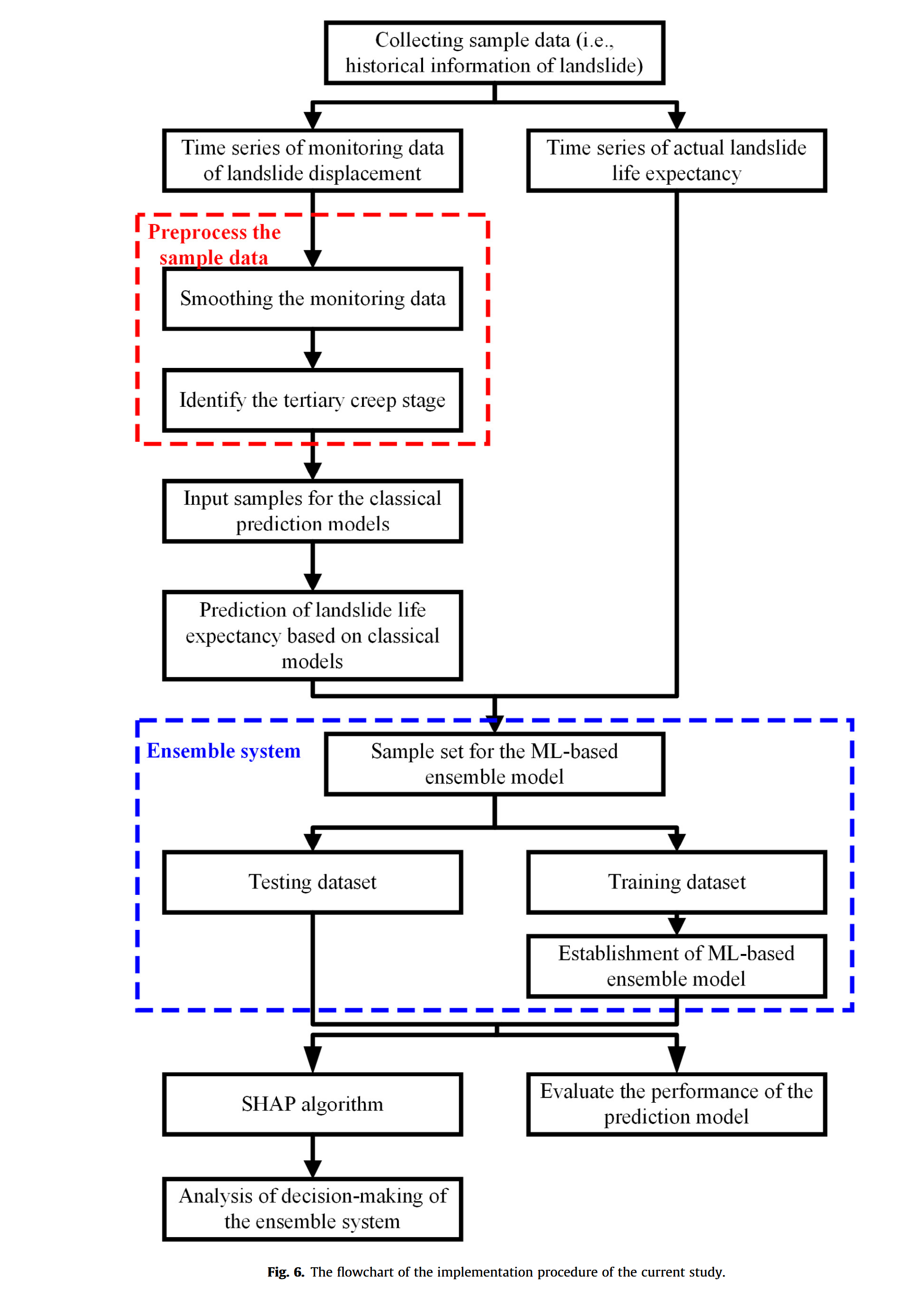
步骤1：收集样本数据，包括滑坡位移监测数据及实际滑坡寿命期的时间序列。

步骤2：对样本数据进行预处理。这里，采用滑动平均法对原始位移监测数据进行平滑处理，然后利用切线角量化方法（详见第4.1节）提取土体的三级蠕变阶段相关数据。需要注意的是，数据预处理后，11条共计204个数据点的滑坡位移时间序列构成了模型建立的样本数据。

步骤3：利用经典预测模型（即Verhulst模型、GM (1,1)模型和Saito模型）进行滑坡失效时间预测。对经典预测模型的性能进行研究，并将经典模型的预测输出作为元模型的输入，用于建立集成系统（见图4）。换言之，经典模型的预测输出构成了集成模型的样本集。

步骤4：将样本集划分为测试集和训练集。

步骤5：使用训练集建立集成模型。

步骤6：使用测试集对集成模型的性能进行评估，评估指标包括MAE、RMSE和不可信指数b。同时，采用SHAP算法分析集成系统的决策过程。

---

5. 结果

5.1 经典模型对滑坡寿命期的预测

本节使用经典预测模型——Verhulst模型、GM (1,1)模型和Saito模型，结合第2节中介绍的11条累计位移监测时间序列，进行滑坡寿命期的预测。这里以动态输入样本（见图3）作为模型建立的数据，研究经典模型在动态预测背景下的表现。以下分别展示数据预处理结果和滑坡寿命期的预测结果。

5.1.1 数据预处理结果

在实施预测模型前，对数据进行处理。采用滑动平均法平滑原始监测数据，并利用切线角量化方法确定土体的三级蠕变阶段（详见第4.1节）。图7展示了滑动平均处理结果及位移—时间（Ti-t）曲线的切线角。可见滑动平均法在滤除噪声方面表现良好。同时，依据切线角阈值（即 $a\_i>45^{\circ }$），确定了每条累计位移时间序列对应的三级蠕变阶段。

5.1.2 经典模型预测结果

将经过平滑处理的三级蠕变阶段相关数据用于模型建立，预测的滑坡寿命期结果如图8所示。从图中可见，GM (1,1)模型在三级蠕变早期阶段的预测寿命期普遍大于其他两模型的预测结果。Verhulst模型在该阶段的预测值大多小于实际寿命期，且在滑坡失效临近时，其预测结果最终超过另外两模型。Saito模型的预测结果较为稳定，且预测精度随着滑坡的发展逐渐提高。如图8所示，滑坡失效临近时，Saito模型在各经典模型中预测最为准确。此外，图8显示Verhulst模型在多数情况下产生无效预测（即预测寿命期小于0），GM (1,1)模型在雷家山滑坡的GNSS 3号和5号传感器数据中也出现无效预测（图8c、8e）。Saito模型虽无无效预测，但其预测结果大多落在不可信区域，表明其在动态预测中的预测质量较差。

---

5.2 集成模型对滑坡寿命期的预测

针对经典模型在动态预测中的不足，为提高预测精度和质量，开发了集成系统，将三种经典模型的预测结果融合，通过机器学习算法建立元模型（详见第4.3节）。在堆叠式集成框架下（图4），机器学习元模型的训练样本即为经典模型的预测输出。因此，本节以图8中经典模型的预测结果作为元模型训练数据。表1列出了样本集的四种划分比例：6:5（图8中6个子图数据作为训练，5个作为测试）、7:4、8:3和9:2。训练时，元模型输入为三种经典模型在某时刻的预测寿命期输出，输出为对应的实际寿命期。元模型采用了前馈神经网络（FNN）、支持向量回归（SVR）和决策树回归（DTR）三种机器学习算法，并比较了它们的性能。图9展示了在9:2划分比例下，集成模型对滑坡寿命期的预测结果。表2列出了不同划分比例下，预测模型的MAE、RMSE及不可信指数b（均基于测试集）。图9可见，随着监测时间接近失效时，机器学习集成模型的预测结果接近实际寿命期。

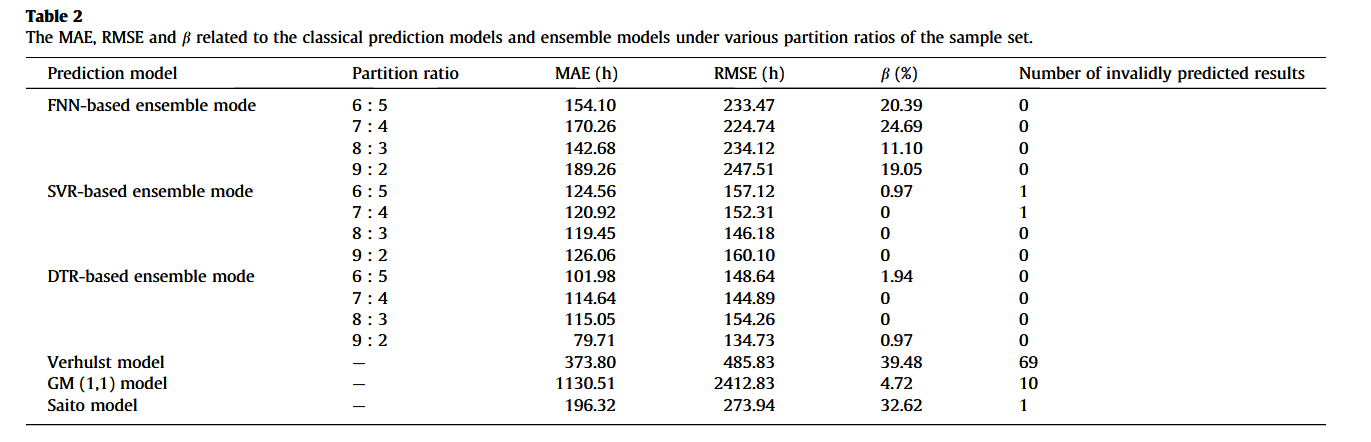
此外，图9显示，基于FNN的集成模型有较多预测结果落入不可信区域；表2也反映出其MAE、RMSE和b值均高于其他集成模型，表明FNN集成模型的预测精度和质量最低。相较之下，DTR集成模型的MAE和RMSE在所有划分比例下均最小，SVR和DTR的b值均较小。但SVR模型在部分情况下产生无效预测（寿命期小于0，见表2），而FNN和DTR模型在所有场景中均无无效预测。因此，综合来看，DTR算法在建立集成系统方面表现最佳。

---

5.3 经典模型与集成模型的比较

本节比较经典模型与集成模型的预测精度和质量。表2显示，GM (1,1)模型的MAE和RMSE明显高于其他模型，预测精度最低。集成模型的MAE和RMSE均小于经典模型，表明集成模型预测结果更准确。SVR和DTR集成模型的b值明显小于其他模型。虽然FNN模型的b值高于GM (1,1)，但其MAE明显小于GM (1,1)。经典模型产生无效预测的次数显著多于集成模型。为直观对比集成与经典模型性能，表3列出了样本集9:2划分下两者评价指标的相对下降率，结果表明集成系统的引入总体降低了经典模型的MAE、RMSE和b值。

基于以上分析，集成模型的预测精度和质量均优于经典模型。

此外，经典模型与集成模型在实际应用场景下的表现对比也在本节进行了讨论。为此，结合了四级预警机制（表4），其对应颜色标识如图10所示。四级预警基于滑坡灾害的紧急程度，广泛应用于工程实践（Fan等，2019）。鉴于仅采用了三级蠕变阶段相关数据预测寿命期，图10中仅显示黄、橙、红三级预警。图10a–d的数据分别来自图8g、8h和图9a、9b。图10c、d显示，尽管集成模型在三级蠕变早期（初始加速阶段）的预测精度较低，但该阶段的预警为黄信号，表明坡体仍处于安全状态。随着滑坡演化，预警级别提升，集成模型的预测精度同步提高，尤其在橙色和红色预警时预测精度显著提升。相比之下，经典模型在橙色预警时预测结果仍表现出较低精度（图10a、10b）。

在动态预测背景下，滑坡演化早期的预测误差若不落入不可信区域，影响较小，因为该阶段预测寿命期可在后续监测周期中利用更多样本不断更新和改进（详见第4.2节）。因此，不可信指数较低的预测方法，在滑坡早期预测误差问题上表现更佳。表2显示，SVR和DTR集成模型的不可信指数显著低于其他模型，表明集成模型在工程实践中更具适用性。

最后，表5和表6列出了雷家山滑坡GNSS 7号和8号站点在黄、橙、红三级预警下，不同模型预测结果的MAE、RMSE及b值。结果显示，机器学习集成模型整体优于经典模型，尤其在橙色和红色预警下表现更优。各信号等级中，DTR集成模型均表现最佳，MAE、RMSE和b值最小。对于经典模型，黄信号下GM (1,1)表现最佳，橙色和红色信号下Saito模型表现最佳（基于MAE、RMSE和b值）。

6. 讨论

6.1 关于集成模型为何优于经典预测模型的讨论

根据第5节所呈现的结果，将经典模型集成到集成系统框架下，其预测精度能够显著提升。特别是，针对经典预测模型出现的无效预测结果问题，集成系统的引入能够明显改善。产生这一现象的原因在于，集成系统能够结合多种经典模型的优势，减弱单个模型“错误预测”的影响。换句话说，单个模型的预测结果经过集成系统的优化后，最终输出的预测值更接近实际的滑坡寿命预期值。此外，在动态预测且失信指数较小的条件下，集成模型的预测质量优于经典模型。这是因为，当预测的滑坡寿命预期值更接近实际值时，位于失信区间内的预测结果比例会减少，如图5所示。

6.2 关于为何DTR优于其他机器学习算法的讨论

本研究中，基于表2的结果，DTR（决策树回归器）在建立集成系统的元模型方面表现最佳。为了进一步验证该结论，本文在样本集划分比例为9:2的条件下，进行了配对t检验（Towfiqul Islam等，2021）。当p值小于0.05时，结论被认为具有显著性。配对t检验结果见表7。由表7可知，DTR在集成系统构建中优于FNN（前馈神经网络）和SVR（支持向量回归）的结论具有统计显著性，p值均小于0.05。
DTR优于其他算法的原因可能有两点：首先，DTR更适应小样本数据集和输入变量低相关性的情况（即图4中经典模型的预测结果Tfp1、Tfp2和Tfp3），因为DTR的训练过程较为简单（Kardani等，2020；Davawala等，2023）。相比之下，FNN的表现最差，具有最高的MAE、RMSE和b值，可能是由于其训练过程较为复杂（例如，训练FNN时需涉及特征处理），因此小样本且低相关性的输入变量不足以构建准确且鲁棒的FNN模型，导致局部最优和训练不足问题出现。其次，从DTR算法理论角度，样本数据集的特征空间可以被划分，这意味着DTR框架下可以近似区分滑坡演化的不同阶段，有利于提高滑坡失效时间预测的准确性。此外，DTR的预测结果是决策区域的平均值，因此使用DTR集成模型时，极端偏差的预测结果较少出现（Géron，2017）。

6.3 关于各经典预测模型对集成系统预测结果影响的讨论

SHAP分析在机器学习领域广泛用于衡量不同输入特征对最终输出的贡献（Zhou等，2022；Al-Najjar等，2023；Ge等，2023）。需要注意的是，在集成系统中，机器学习元模型的输入因素是经典预测模型的输出。因此，本研究采用SHAP分析探讨构成集成系统的各经典预测模型（即Verhulst模型、GM(1,1)模型和Saito模型）对集成系统最终预测结果的影响。这里的SHAP分析基于表现最佳的DTR集成模型进行。图11展示了考虑图10中所有样本的Verhulst、GM(1,1)和Saito模型的SHAP值。由图11可见，Verhulst模型和Saito模型产生的较大输出值一般会促进滑坡寿命预期预测值的增加，意味着滑坡失效时间预测被推迟。此外，GM(1,1)模型输出对最终预测结果的贡献度明显低于其他经典模型。

6.4 关于本研究的局限性及未来展望的讨论

本研究由于样本数据集较小，采用了机器学习算法构建集成系统，而非深度学习算法。样本数据集较大时，机器学习算法的表现可能不及深度学习算法，此时深度学习算法可能是构建集成系统元模型的更优选择，建议作为未来研究方向。此外，本研究旨在初步探索考虑监测数据动态变化条件下，集成系统在滑坡失效时间预测中的可行性。目前基于机器学习的集成系统预测结果在滑坡灾害防控实践中可能仍不够理想，采用深度学习算法构建集成系统元模型有望进一步提升预测准确度和质量。
另外，适当的超参数设置可提升机器学习算法的预测性能（Zhou等，2016），超参数可通过遗传算法（Cai等，2016）、贝叶斯优化（Yang等，2022）和灰狼优化算法（Zhang等，2020）等优化方法获得。但进行超参数优化时，数据集需划分为训练集、测试集和用于确定最优超参数的数据集。考虑到当前研究中样本数据集较小，超参数优化可能不适用，因此本研究采用Python中的默认超参数设置。尽管如此，超参数优化仍是提升集成系统预测精度和质量的有效途径，值得未来深入研究。

7. 结论

本文结合4个真实滑坡案例的11组累计位移时间序列，研究了经典预测模型（即Verhulst、GM(1,1)和Saito模型）在滑坡寿命动态预测中的性能。为提高动态预测的精度和质量，提出了基于机器学习元模型的集成系统，将经典预测模型进行集成。此外，本文引入失信指数以评价动态预测下模型的预测质量，失信指数越高表示预测质量越低。主要结论如下：
(1) 本研究揭示了经典预测模型在动态预测下的不足。Saito和Verhulst模型预测的滑坡寿命存在较高失信指数，说明这两模型在动态预测中的表现不佳。GM(1,1)模型的预测准确度在各模型中最低。
(2) 通过集成系统框架集成经典预测模型，预测准确度和质量均得到提升。且集成模型在滑坡的四级预警机制下适用性优于经典模型。集成模型在橙色和红色预警信号下预测精度足够高，满足紧急预测需求，而经典模型在橙色预警信号下仍表现不佳。
(3) 在构建集成系统元模型所用机器学习算法中，DTR表现最佳，而FNN表现最差。