常用操作符,操作符相关笔试题(谷歌)及算法的优化(上)
目录
- 一、进制的转换
- 1.1 10进制转2进制数字
- 1.2 2进制转8进制
- 1.3 2进制转16进制
- 二、原码、反码、补码
- 三、移位操作符
- 3.1 左移操作符
- 3.2 右移操作符
- 四、位操作符:&、|、^、~
- 4.1 面试题1
- 4.2 面试题2(最早出现于谷歌面试题)
- 4.3 面试题3
- 五、逗号表达式
- 六、[ ]下标引用操作符
- 七、函数调用操作符
- 总结
前言
这篇内容想了想打算不细节的写了,只写我认为需要写的部分,因为有的操作符太简单了,而且也在我之前的文章写到过一些。
一、进制的转换
1.1 10进制转2进制数字
2 125 余数为12 62 余数为02 31 余数为12 15 余数为1 2 7 余数为12 3 余数为12 1 余数为10
这里是什么意思呢?
就是125/2商62余1,以此类推,最后最左边的余数行由下往上依次所得得余数就是10进制转换出的2进制
1.2 2进制转8进制
8进制的数字每一位是0-7,0-7的数组,各自写成2进制,最多有3个2进制位就足够了,比如7的二进制是111,所以在2进制转8进制的时候,从2进制序列中右边低位开始向左每3个2进制位会换算一个8进制位,剩余不够3个二进制位的直接换算
如:2进制的01101011,换成8进制:0153,0开头的数字,会被当成八进制
2进制 01 101 011
8进制 1 5 3

1.3 2进制转16进制
16进制的数字每一位是0-9,a-f的数字,各自写成2进制,最多有4个2进制位就足够了,比如f的二进制是1111,所以在2进制转16进制数的时候,从2进制序列中右边低位开始向左每4个2进制位会换算一个16进制位,剩余不够4个二进制位的直接换算
2进制 0110 1011
16进制 6 b
而且想找10进制对应的二进制数的时候,也有便捷的方法
2进制: 1 1 1 1 1 1 1 1128 64 32 16 8 4 2 11 0 0 0 1 1
比如说这里找35对应的二进制数,32+2+1等于35,在对应的位置下的二进制取1,其余位取0就可
二、原码、反码、补码
整数的2进制表示方法有三种,即原码、反码和补码
有符号整数的三种表示方法均有符号位和数值位两部分,2进制序列中,最高位的1是被当做符号位,剩余的都是数值位。对于无符号整数来说,全部都是数值位
符号位都是用0表示”正“,用1表示”负"
正整数的原、反、补码都相同
负整数的三种表示方法各不相同
原码:直接将数值按照正负数的形式翻译成二进制得到的就是原码
反码:将原码的符号位不变,其他位依次按位取反就可以得到反码
补码:反码+1就得到补码
补码得到原码也可以使用:取反,+1的操作
用下面两张图来表示:


附以代码,整型是32个比特位
int main()
{int a = 10;//00000000000000000000000000001010 -> 原码//00000000000000000000000000001010 -> 反码//00000000000000000000000000001010 -> 补码int b = -10;//10000000000000000000000000001010 -> 原码//11111111111111111111111111110101 -> 反码//11111111111111111111111111110110 -> 补码//11111111111111111111111111110110 -> 补码//10000000000000000000000000001001 -> 取反//10000000000000000000000000001010 -> 原码return 0;
}
对于整型来说:数据存放在内存中其实存放的就是补码
为什么呢?
- 在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统一处理;同时,加法和减法也可以统一处理(CPU只有加法器,即CPU默认只能算加法)此外,补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路,但在程序中打印出来的是原码。
这里也附加代码更好理解
int main()
{//1-1//1 + (-1)//假设按照原码计算//00000000000000000000000000000001 --> 原码 1//10000000000000000000000000000001 --> 原码 -1//10000000000000000000000000000010 --> -2////再使用补码计算//00000000000000000000000000000001 - 补码//10000000000000000000000000000001 - 原码//11111111111111111111111111111110 - 反码//11111111111111111111111111111111 - 补码//00000000000000000000000000000001 - 补码//00000000000000000000000000000000 - 这里是把高位去掉留低位,这样打印出来的值就正确了return 0;
}
三、移位操作符
**<<**左移操作符
**>>**右移操作符
注:移位操作符的操作数只能是整数
3.1 左移操作符
移位规则:左边抛弃、右边补0


3.2 右移操作符
移位规则:首先右移运算分两种:
- 逻辑右移:左边用0填充。右边丢弃
- 算数右移,左边用原该值的符号位填充,右边丢弃
右移到底是逻辑右移还是算术右移取决于编译器,大部分编译器上都采用算数右移的,例如VS2022:

注意:对于移位运算符,不要移动负数位,这个是标准未定义的。
四、位操作符:&、|、^、~
位操作符有:
& //按位与
| //按位或
^ //按位异或
~ //按位取反
注:这里的位都是二进制位的意思,且他们的操作数必须是整数
分别用代码展示
4.1 面试题1
题目:不能创建临时变量(第三个变量),实现两个整数的交换
正常思路便是创建第三个变量,如下图:

这里实现醋和酱油的互换便是先将酱油放到空瓶里,再把醋倒进酱油瓶,最后将空瓶中的酱油倒进醋瓶里。
代码实现如下
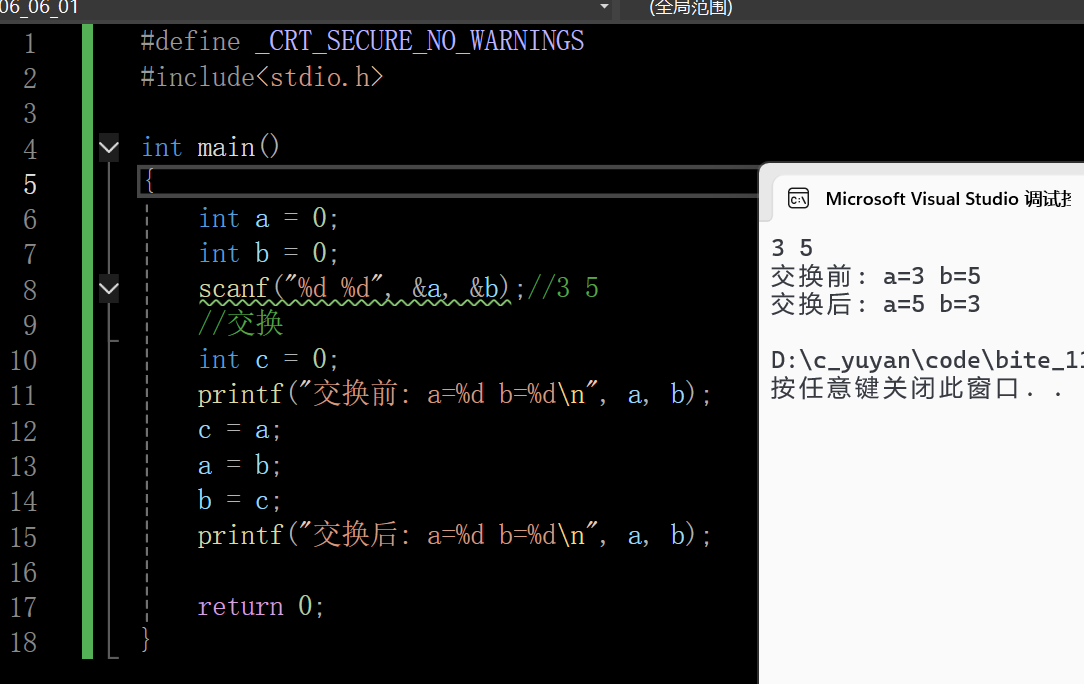
Plan B

没什么好说的,略加分析就能明白,虽然实现了功能,但是有一定的缺陷,一个整型变量存放的值一定有它的上限,一个整型变量最大就四个字节,一但a,b特别大,加起来超过了能放的最大值,此时就会丢失一些位,也就是存在数据溢出的风险。
那么能不能把刚刚的操作符知识应用到这个题目里呢?

这里就要补充一下异或的特点了,0与任何数异或都是那个数,且异或是支持交换率的。
3 011
5 101
^ 110
3 011
5 101
这里3先与5异或,异或出来的值再与3异或,得到的值还是5
Plan C

这个代码的优点就是异或运算的过程中并不会产生进位,所以不会出现溢出的情况,当然对应的缺点就是不容易想到,可读性差。
4.2 面试题2(最早出现于谷歌面试题)
题目:求一个整数存储在内存中二进制中1的个数
15 -->4(1的个数)
补码:
00000000000000000000000000001111
-1 -->32(1的个数)
10000000000000000000000000000001 -原码
11111111111111111111111111111110 -反码
11111111111111111111111111111111 -补码
首先先分析题目内存中二进制,即内存中二进制的补码形式。
首先这里的思路就是求它二进制的每一位,再判断这一位是否是1,是就++。在之前十进制获得每一位的方法是%10取到最后一位,再/10去掉最后一位。这里二进制也可以与之对应,即先%2再/2,这就形成了一个循环,循环终止条件就是这个数变为0,这时候必定一个1也没有了。
比如15%2=7…1得到的便是00000000000000000000000000001111的最后一个1,之后再10/2==7去掉该1,就得到00000000000000000000000000000111转到十进制就是7了。
Plan A

补充:这里count是统计的作用,判断这一位是1后便++,直到n变为0,此时便一个1也没有了,因为0的二进制便是32个0。
且无论这个位是0还是1,这一位统计之后都要去掉,所以n/=2。
但是呢,这个程序其实是有问题的:
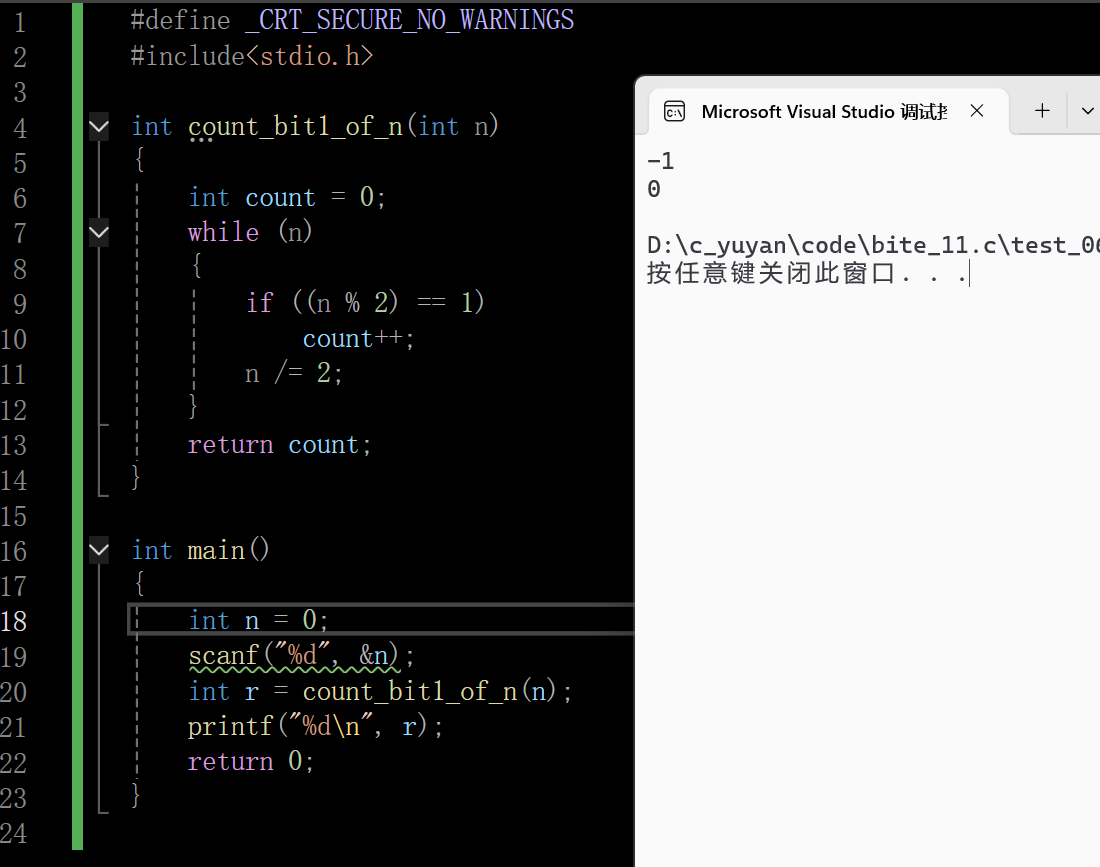
在输入-1的时候,发现本应输出32缺输出了0,原因是-1%2=-1,-1/2=0,进入一次循环后便结束了。所以这串代码的功能只对0和正整数有效。
Plan B
这里提供第二种方法便是按位取与(&)
思路便是
15 -->4(1的个数)
补码:
00000000000000000000000000001111
1的补码
00000000000000000000000000000001
对应的二进制位进行与运算,只要有0则为0,两个同时为1,才为1
这里15的补码与1的补码按位与运算,最后一位与的结果是1,其他位与的结果都是0,这就说明最低位是1,反之。统计完该位后,向右移动一位便可去掉该位,一共32位,最高位0移动31位就够了,每移动一位便说明有一个1。
代码实现如下:

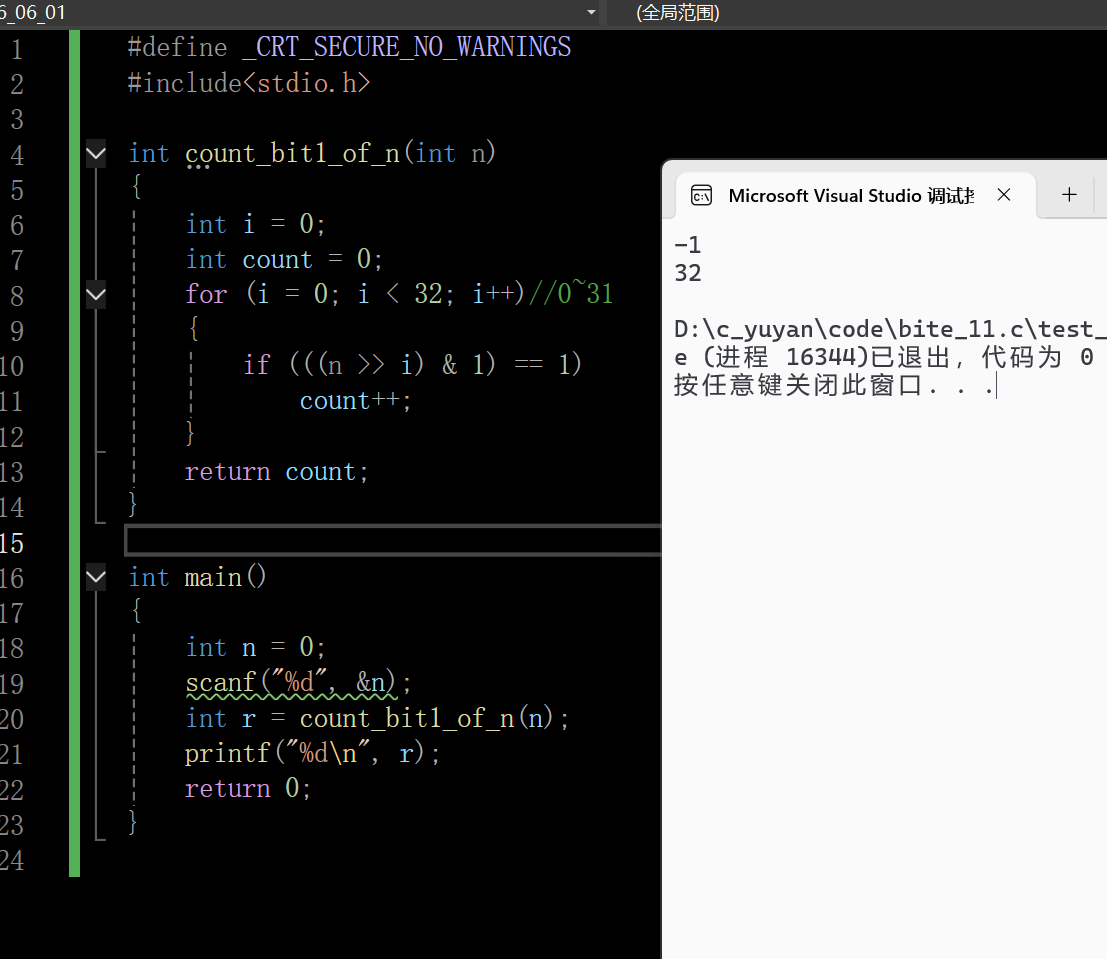
可以看到这串代码负数也是能正常实现的,但是呢,它还是存在缺点的,这里需要循环32次,效率不是很高,而且无论几个1,它都会循环32次。
Plan C
改进之前先介绍一种算法:
n=15 -> 1111(15二进制形式有4个1)
n = n & (n-1) //下面为该公式逻辑展示n = 1111
n - 1 = 1110
&n = 1110
n - 1 = 1101
& n = 1100
n - 1 = 1011
&n = 1000
n - 1 = 0111
&n = 0000
可以发现n=n&(n-1)这个算法,每一次取与,都会去掉一个1,在变为0000之前,该取与执行几次,就去掉几个1,负数也是一样的,这里不再做推演


这就是谷歌的一个以前的一个笔试题,试想,面试官肯定想要的不是第一种和第二种代码吧。
这里还可以进行扩展:
题目:判断n是否是2的次方数?
4 = 2的平方 00100
8 = 2的三次方 01000
9不是2的平方
可以看到次方数都有一个特点,他们的二进制数都只有一个1,因此我们就可以用这串代码来判断:
if(n&(n-1) == 0)
{就是次方数;
}
经过该算法取余之后,仅有的一个1就没有了,就变为0了。
代码展示


4.3 面试题3
题目:二进制位置0或者置1
1的二进制序列: 00000000000000000000000000000001左移4位: 00000000000000000000000000010000
13的2进制序列: 00000000000000000000000000001101
将第5位置置为1后 00000000000000000000000000011101
将第5位再置位0后 00000000000000000000000000001101
这里的思路就是将1的二进制数左移4位,再按位取或,按位或,是对应的二进制位进行或运算,只要有1,就是1,两个同时为0才为0,这样13经过按位取或之后第五位就能变1
第五位再置0稍微麻烦一些,现是将1左移4位
1的二进制序列: 00000000000000000000000000000001
1的二进制序列左移 00000000000000000000000000010000取反 11111111111111111111111111101111
将第5位置置为1后 00000000000000000000000000011101取与 00000000000000000000000000001101
13的2进制序列: 00000000000000000000000000001101
取与后的值是不是与13的2进制序列一样呢?
下面这样省略了0看起来更简洁一些,而且能够对齐
13 = 00001101
| 00010000000111011<<(5-1) //这里5-1的原因是将第五位修改为1,可作为固定公式
29 = 00011101
& 11101111 >-< 00010000 1<<(5-1)00001101
所以该程序的代码就是这样的:

五、逗号表达式
exp1,exp2,exp3,...expN
逗号表达式,就是用逗号隔开多个表达式。
逗号表达式,从左到右依次执行,整个表达式的结果是最后一个表达式的结果,例下几张代码:

int d = 0;
if (a = b + 1, c = a / 2, d > 0)
{}
这里if里面的判断条件就主要看d>0这里
逗号表达式也能优化一些代码,如下:
a = get_val();
count_val(a);
while (a > 0)
{//业务处理//...a = get_val();count_val(a);
}
这样一个循环如何用逗号表达式进行优化呢?
while (a = get_val(), count_val(a), a > 0)
{//业务处理
}
六、[ ]下标引用操作符
操作数:一个数组名+一个索引值(下标)
int arr[10] = {0};arr[5] = 8;//[] - 下标引用操作符
//arr , 5是[]的两个操作数
七、函数调用操作符
接受一个或者多个操作数:第一个操作数是函数名,剩余的操作数就是传递给函数的参数
int Add(int x, int y)
{return x + y;
}void test()
{}int main()
{printf("hehe"); //()是函数调用操作符int r = Add(3, 5);//()是函数调用操作符//()也是有操作数:函数名和参数都是()的操作数test();return 0;
}
函数调用操作符至少一个操作数,因为其函数可能无参数。
总结
该篇文章主要囊括了常见的操作符,涉及操作符的相关面试笔试题,其中还有一些算法的优化,还是干货满满的,希望喜欢作者文章的兄弟们点赞支持一下,你们的支持就是我最大的动力~




