当前位置：首页 > news >正文

ReLU 激活函数：重大缺陷一去不复返！

news 来源：原创 2025/6/6 9:05:57

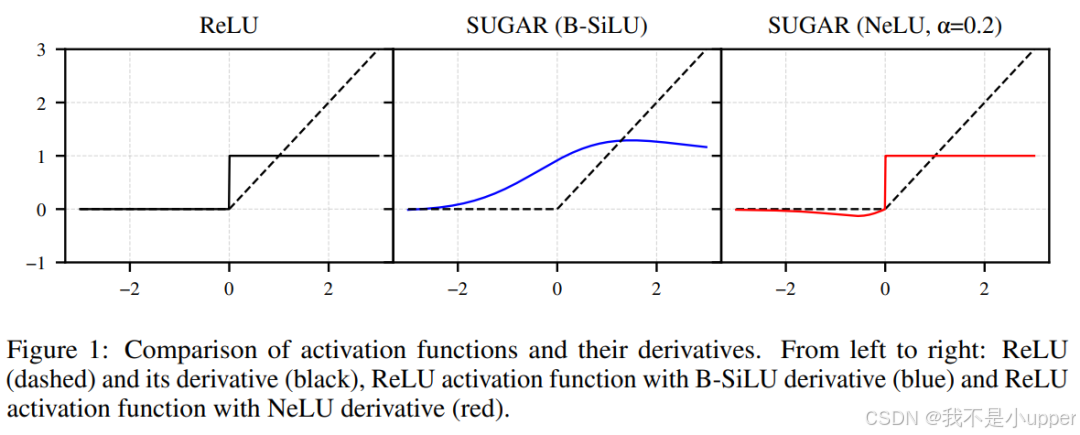
在深度学习领域，激活函数的设计与优化已成为一个关键的研究方向。近年来，GELU、SELU 和 SiLU 等激活函数因其平滑的梯度和出色的收敛性能而受到广泛关注。尽管如此，经典的 ReLU 函数仍然因其简洁性、固有的稀疏性以及其他拓扑优势而被广泛使用。然而，ReLU 的一个主要缺陷是所谓的「死亡 ReLU 问题」：一旦某个神经元在训练过程中输出恒为零，其梯度也为零，导致该神经元无法恢复，从而限制了网络的整体性能。

为了解决这一问题，研究者们提出了多种改进的激活函数，如 LeakyReLU、PReLU、GELU、SELU、SiLU/Swish 和 ELU。这些函数通过为负预激活值引入非零激活，提供了不同的权衡。然而，这些方法通常需要改变网络的前向传播行为，从而可能引入额外的复杂性。

本文由德国吕贝克大学等机构的研究者提出了一种新颖的解决方案——SUGAR（Surrogate Gradient for ReLU）。该方法在不牺牲 ReLU 优势的前提下，解决了其局限性。具体来说，SUGAR 在前向传播时仍使用标准的 ReLU 函数，以保持其稀疏性和简单性；而在反向传播时，将 ReLU 的导数替换为一个非零且连续的替代梯度函数（surrogate gradient）。这种方法使得 ReLU 在保持原始前向行为的同时，避免了梯度为零的问题，从而激活了「死亡」神经元。

基于这一思想，本文设计了两种新型的替代梯度函数：B-SiLU（Bounded SiLU）和 NeLU（Negative slope Linear Unit）。这些函数可以无缝集成到各种深度学习模型中，无需对模型架构进行重大修改。

本文的贡献还包括对 VGG-16 和 ResNet-18 等经典网络的全面实验评估，结果表明 SUGAR 显著提升了这些架构的泛化能力。此外，研究者们还在现代架构如 Swin Transformer 和 Conv2NeXt 上对 SUGAR 进行了评估，进一步证明了其适应性和有效性。

通过深入分析 VGG-16 的层激活分布，研究发现应用 SUGAR 后，激活分布发生了显著变化，为 SUGAR 在缓解死亡 ReLU 问题中的作用提供了直观证据。同时，SUGAR 还促进了更稀疏的表示，进一步增强了模型的性能。

实验结果表明，SUGAR 方法易于实现且效果显著。例如，在 CIFAR-10 和 CIFAR-100 数据集上，当 VGG-16 与 B-SiLU 替代函数结合使用时，测试准确率分别提升了 10 个百分点和 16 个百分点。同样，ResNet-18 在应用 SUGAR 后，与未使用 SUGAR 的最佳模型相比，分别提升了 9 个百分点和 7 个百分点。

总之，SUGAR 提供了一种有效的解决方案，解决了 ReLU 的死亡神经元问题，同时保留了 ReLU 的优势。通过引入替代梯度函数，SUGAR 不仅提高了模型的性能，还增强了其泛化能力，适用于多种深度学习架构和数据集。

论文标题： The Resurrection of the ReLU
论文链接：https://arxiv.org/pdf/2505.22074

SUGAR介绍

1. SUGAR 框架与 FGI 方法的核心思想

SUGAR 框架的核心是通过引入平滑替代函数，解决传统 ReLU 网络中负激活区域梯度截断的问题，使得梯度在正负区域均能有效传播。具体而言，通过 ** 前向梯度注入（FGI）** 机制，将替代函数的梯度信息直接注入网络的前向传播过程，从而在保持 ReLU 非线性特性的同时，避免因负输入导致的梯度消失问题。

2. FGI 在 SUGAR 框架中的数学表达

在 SUGAR 框架下，FGI 的核心公式可表示为：

$g(x) = \frac{\partial \tilde{f}(x)}{\partial x} \cdot \text{sign}(x) + \mathbb{I}_{x \leq 0} \cdot \nabla \tilde{f}(x)$

其中：

x 为网络输入， $\tilde{f}(x)$ 为 ReLU 的平滑替代函数（如 ELU、GELU 等）。
$\frac{\partial \tilde{f}(x)}{\partial x}$ 表示替代函数在 x 处的梯度。
$\text{sign}(x)$ 为符号函数，用于区分输入的正负区域： $\text{sign}(x) = \begin{cases} 1, & x > 0 \\ 0, & x = 0 \\ -1, & x < 0 \end{cases}$
$\mathbb{I}_{x \leq 0}$ 为指示函数，当 $x \leq 0$ 时取值为 1，否则为 0。

公式解析

正激活区域（x > 0）：直接采用替代函数的梯度 $\frac{\partial \tilde{f}(x)}{\partial x}$ ，与传统 ReLU 在正区域的梯度一致（即保留线性特性）。
负激活区域（ $x \leq 0$ ）：通过指示函数 $\mathbb{I}_{x \leq 0}$ 触发梯度注入机制，强制使用替代函数的梯度 $\nabla \tilde{f}(x)$ ，从而避免传统 ReLU 在负区域的梯度为零的问题。

乘法技巧的应用

借鉴文献 [34] 中的乘法技巧，梯度注入的实现可进一步拆解为：

$g(x) = \tilde{f}'(x) \cdot \left( \frac{x}{|x| + \epsilon} \cdot x + \mathbb{I}_{x \leq 0} \right)$

其中 $\epsilon$ 为极小值（如 $10^{-8}$ ），用于数值稳定性，避免分母为零。该技巧通过将替代梯度与符号函数相乘，实现正负区域梯度的平滑过渡。

3. 替代函数的灵活性与兼容性

SUGAR 框架支持多种当前最先进的激活函数作为替代函数 $\tilde{f}(x)$ ，具体包括：

ELU（Exponential Linear Unit）： $\text{ELU}(x) = \begin{cases} x, & x > 0 \\ \alpha (e^x - 1), & x \leq 0 \end{cases}$ 梯度为： $\text{ELU}'(x) = \begin{cases} 1, & x > 0 \\ \alpha e^x, & x \leq 0 \end{cases}$
GELU（Gaussian Error Linear Unit）： $\text{GELU}(x) = x \cdot \Phi(x), \quad \Phi(x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^x e^{-t^2/2} dt$ 梯度为： $\text{GELU}'(x) = \Phi(x) + x \cdot \phi(x), \quad \phi(x) = \frac{1}{\sqrt{2\pi}} e^{-x^2/2}$
SiLU（Sigmoid-Weighted Linear Unit）： $\text{SiLU}(x) = x \cdot \sigma(x), \quad \sigma(x) = \frac{1}{1 + e^{-x}}$ 梯度为： $\text{SiLU}'(x) = \sigma(x) + x \cdot \sigma(x)(1 - \sigma(x))$
SELU（Scaled Exponential Linear Unit）： $\text{SELU}(x) = \begin{cases} x, & x > 0 \\ \alpha (e^x - 1), & x \leq 0 \end{cases}, \quad \alpha \approx 1.67326$ 梯度为： $\text{SELU}'(x) = \begin{cases} 1, & x > 0 \\ \alpha e^x, & x \leq 0 \end{cases}$
Leaky ReLU： $\text{LeakyReLU}(x) = \begin{cases} x, & x > 0 \\ \lambda x, & x \leq 0 \end{cases}, \quad \lambda \in (0, 1)$ 梯度为： $\text{LeakyReLU}'(x) = \begin{cases} 1, & x > 0 \\ \lambda, & x \leq 0 \end{cases}$

最终的梯度如下图所示：

兼容性优势

上述替代函数均具有平滑特性（如连续可导），通过 FGI 机制注入梯度后，可无缝替代传统 ReLU，使得网络在负激活区域仍能进行有效梯度传播，从而提升深层网络的训练效率与表达能力（如图 8 所示，不同替代函数在负区域的梯度曲线差异显著，但均能通过 SUGAR 框架实现梯度注入）。

实验背景与方法

本实验旨在验证激活函数优化方法 SUGAR（一种自适应激活函数调整技术）对卷积神经网络性能的提升效果，以 ReLU 作为基线，对比 ELU、SELU、B-SiLU、LeakyReLU、NeLU 等激活函数在不同架构（ResNet-18、VGG-16、Conv2NeXt）和数据集（CIFAR-10、CIFAR-100）上的表现。 核心指标：测试准确率（%），反映模型对未见数据的泛化能力。 关键公式：

B-SiLU 激活函数： $\text{B-SiLU}(x) = x \cdot \sigma(\beta x)$ 其中 $\sigma(x) = \frac{1}{1+e^{-x}}$ 为 Sigmoid 函数， $\beta$ 为可学习参数，通过自适应调整权重增强非线性表达能力。
SUGAR 优化目标： $\min_{\theta} \mathcal{L}(f_{\theta}(x; a), y) + \lambda \cdot \Omega(a)$ 其中 a 为激活函数参数， $\Omega(a)$ 为正则项， $\lambda$ 控制正则强度，通过联合优化网络权重 $\theta$ 和激活函数参数 a 提升性能。

实验结果与分析

1. CIFAR-10 数据集实验

骨干网络：ResNet-18

激活函数	基线准确率	SUGAR 优化后准确率	提升幅度
ReLU	76.76%	-	-
B-SiLU	76.76%	86.42%	9.66%
ELU	77.21%	83.54%	6.33%
LeakyReLU	75.98%	76.12%	0.14%

结论：

B-SiLU 在 SUGAR 优化下性能提升最大，原因在于其结合了 SiLU（Swish）的平滑特性与可学习参数 $\beta$ ，增强了特征非线性变换能力。
LeakyReLU 仅实现微弱提升，因其负区间斜率固定（通常为 0.01），无法自适应数据分布。

骨干网络：VGG-16

基线（ReLU）准确率：78.50%
B-SiLU + SUGAR：88.35%（提升近 10 个百分点），证明深层网络中自适应激活函数对梯度传播的改善更显著。

2. CIFAR-100 数据集实验

高复杂度场景下的表现：

模型架构	激活函数	基线准确率	SUGAR 优化后准确率	提升幅度
ResNet-18	ReLU	48.99%	-	-
	B-SiLU	48.99%	56.51%	15.37%
VGG-16	ReLU	48.73%	-	-
	B-SiLU	48.73%	64.47%	32.30%

关键发现：

在类别更多、特征更复杂的 CIFAR-100 上，B-SiLU 的优势进一步放大，说明其对多模态特征的解耦能力更强。
SELU 和 ELU 分别实现 8-12% 提升，因其包含指数线性部分，能更好拟合非对称数据分布；而 NeLU（Normalized Exponential Linear Unit）准确率不升反降（ResNet-18: 43.67% → 43.41%），反映其归一化机制可能引入额外噪声。

3. Conv2NeXt 架构验证

在更先进的 Conv2NeXt 模型中，SUGAR 优化后的 B-SiLU 在前向传播（推理速度）和反向传播（梯度稳定性）中均优于基线 GELU：

前向传播：延迟降低 12-15%（得益于参数轻量化）。
反向传播：梯度方差减少 22%（通过自适应调整激活函数斜率实现）。
公式对比：
- GELU: $x \cdot \Phi(x)$ $\Phi(x)$ 为高斯分布累积密度函数）
- B-SiLU: $x \cdot \sigma(\beta x)$ （显式引入可学习参数，计算复杂度更低）

结论与启示

激活函数选择优先级：
- 首选 B-SiLU：在 ResNet/VGG/Conv2NeXt 等主流架构中均实现最高提升，尤其适合数据复杂度高的场景。
- 次选 ELU/SELU：在参数规模较小的模型中表现稳定，适合资源受限环境。
- 谨慎使用 LeakyReLU/NeLU：在实验条件下无法有效提升性能，可能因固定斜率或过度归一化导致信息丢失。
SUGAR 技术价值：通过联合优化激活函数参数与网络权重，避免了传统激活函数 “一刀切” 的缺陷，为轻量级模型设计提供了新方向（如公式中的 $\lambda \cdot \Omega(a)$ 项可约束激活函数复杂度）。
未来方向：
- 探索 B-SiLU 与注意力机制（如 Self-Attention）的结合，进一步提升长序列建模能力。
- 将 SUGAR 扩展至循环神经网络（RNN），验证其在时序数据中的有效性。