数据结构——四十四、平衡二叉树的删除操作(王道408)
文章目录
- 前言
- 一.平衡二叉树的删除操作的要求
- 二.平衡二叉树的删除操作
- 1.思路
- 2.具体例子
- 1.经过调整未出现不平衡向上传导
- 1.调整儿子
- 2.调整孙子
- 2.经过调整出现不平衡向上传导(可能不会考)
- 三.知识回顾与重要考点
- 结语
前言
平衡二叉树的删除操作需要确保删除后仍保持二叉排序树特性和平衡性。删除步骤包括:1)按二叉排序树规则删除节点;2)向上查找最小不平衡子树;3)确定最高儿子和孙子;4)根据孙子位置(LL/RR/LR/RL)进行相应旋转调整。删除后若不平衡向上传导,需继续调整。文中通过删除55和32两个实例,分别展示了仅调整儿子节点和需要调整孙子节点的两种情况,并说明旋转后可能出现的不平衡传导现象。关键点在于通过旋转操作恢复平衡,同时保持二叉排序树的有序性。
一.平衡二叉树的删除操作的要求
- 删除结点后,要保持二叉排序树的特性不变(左<中<右)
- 若删除结点导致不平衡,则需要调整平衡
二.平衡二叉树的删除操作
1.思路
- 删除结点(方法同“二叉排序树”)
若删除的结点是叶子,直接删。
若删除的结点只有一个子树,用子树顶替删除位置
若删除的结点有两棵子树,用前驱(或后继)结点顶替,并转换为对前驱(或后继)结点的删除。 - 沿着父节点方向找到最小不平衡子树,找不到就完结撒花
- 找最小不平衡子树下,“个头”最高的儿子、孙子
- 根据孙子的位置,调整平衡(LL/RR/LR/RL)
孙子在LL:儿子右单旋
孙子在RR:儿子左单旋
孙子在LR:孙子先左旋,再右旋
孙子在RL:孙子先右旋,再左旋 - 如果不平衡向上传导,继续2这个操作
对最小不平衡子树的旋转可能导致树变矮,从而导致上层祖先不平衡(不平衡向上传递)
2.具体例子
1.经过调整未出现不平衡向上传导
1.调整儿子
- 删除55这个元素后,将其恢复平衡且依然满足二叉排序树规则
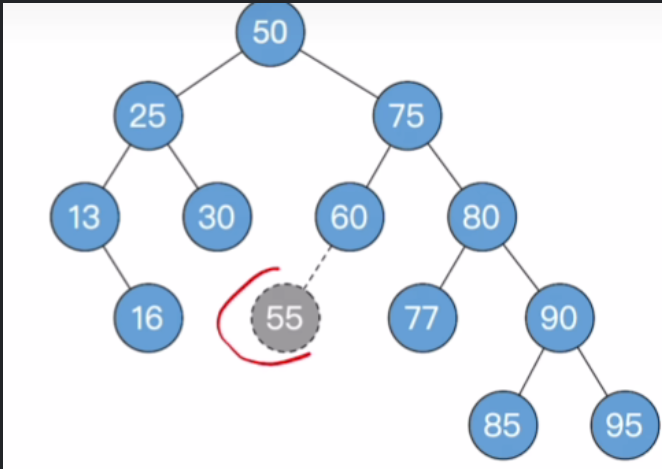
- 从55这个位置出发,沿着父节点的方向向上找到了60这个元素,其左右子树高度差为0,因此不属于最小不平衡子树
- 再往上走是75,其左右子树高度之差为-2,属于最小不平衡子树
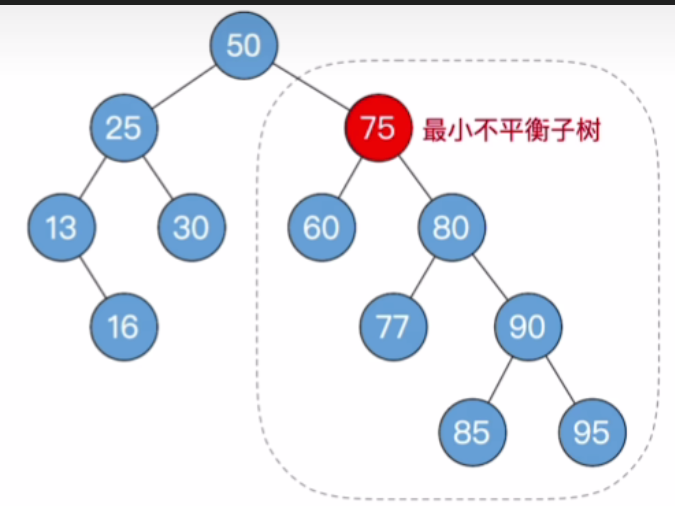
- 75有两个儿子60和80,很显然,80这个儿子比60更高,接下来再从他最高的这个儿子80往下找,找最高的孙子,很显然是90
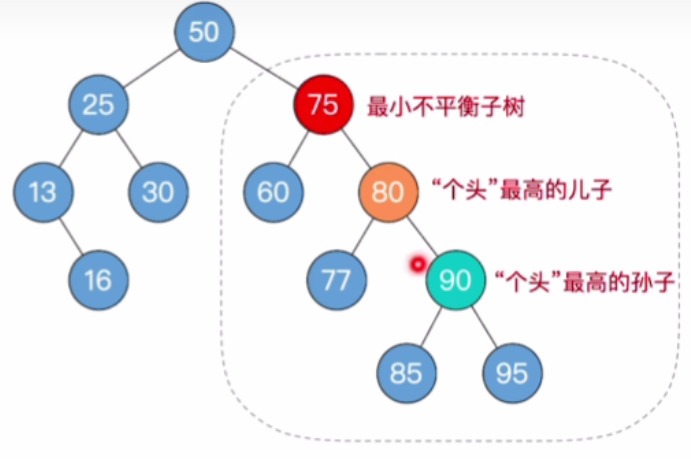
- 由于孙子90在RR,所以儿子80左单旋
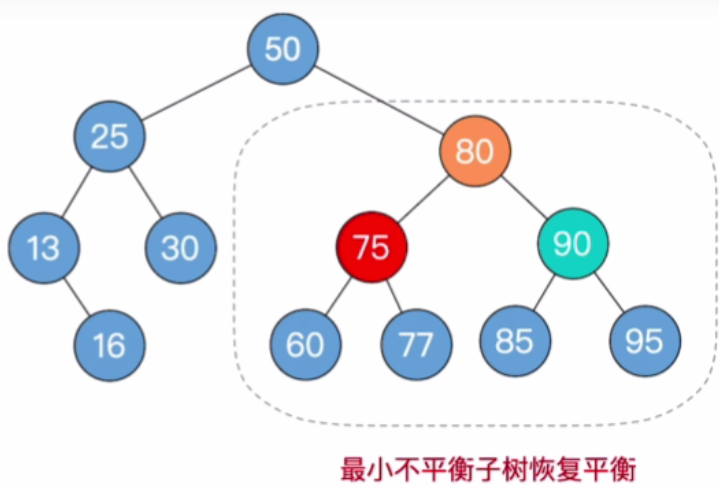
- 由于刚才在我们调整平衡之前,我们的这颗树它的总高度是四,而我们进行左旋操作之后,它的总高度从4变成了3,就有可能会导致它上面的这些祖先进一步的产生不平衡的现象(不平衡向上传递)
- 这里显然没有出现这种情况,因此完成操作
2.调整孙子
- 删除32这个元素后,将其恢复平衡且依然满足二叉排序树规则
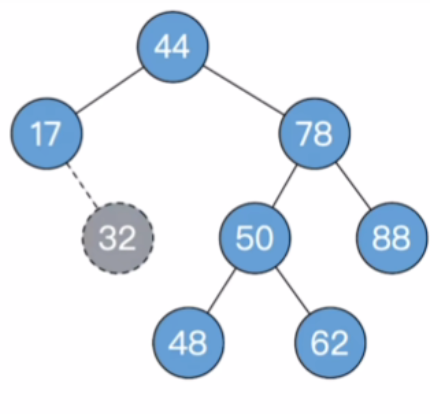
- 根据二叉排序树的删除规则,32是叶子结点,可以直接删除
- 从32沿着其父结点向上,找到44为最小不平衡二叉树的根结点
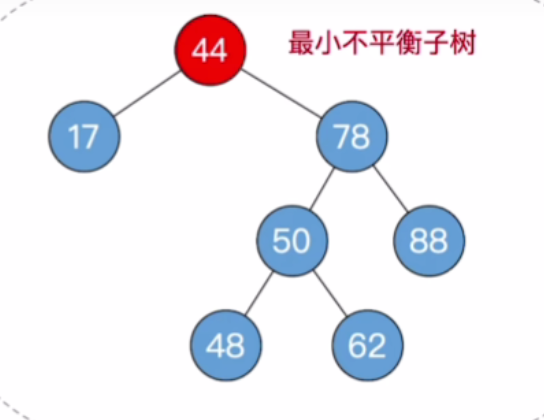
- 44下个头最大的儿子是78,78下个头最大的孙子是50,所以孙子是RL类型的,因此对孙子50进行先右旋再左旋的双旋操作
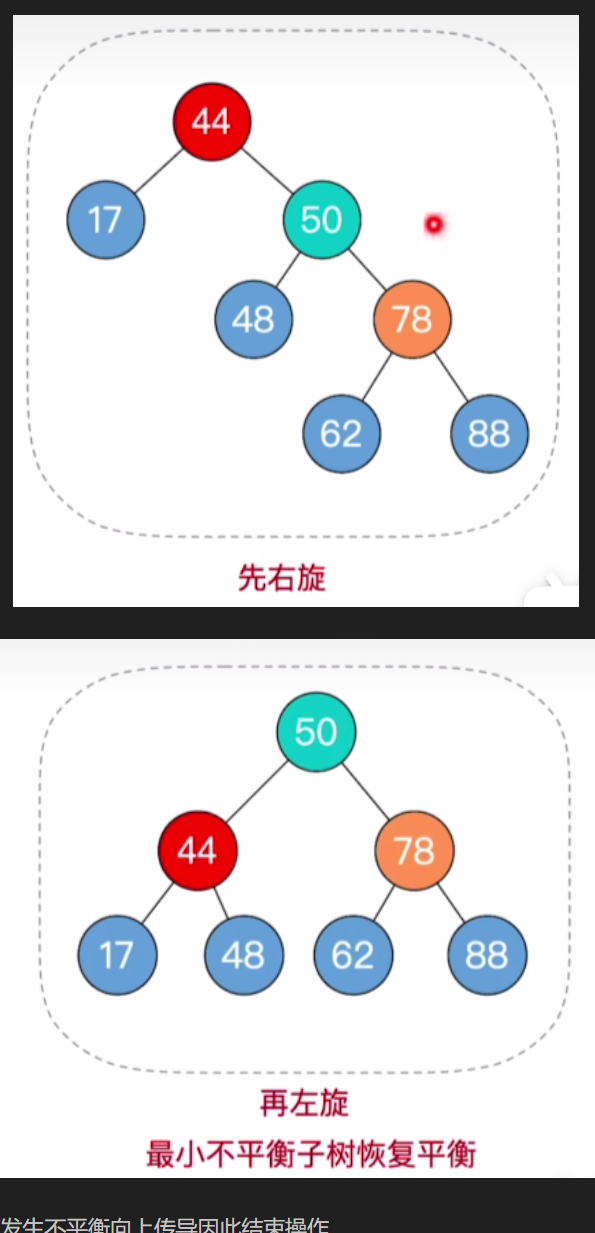
- 经过调整后,并没有发生不平衡向上传导因此结束操作
2.经过调整出现不平衡向上传导(可能不会考)
- 删除32这个元素后,将其恢复平衡且依然满足二叉排序树规则
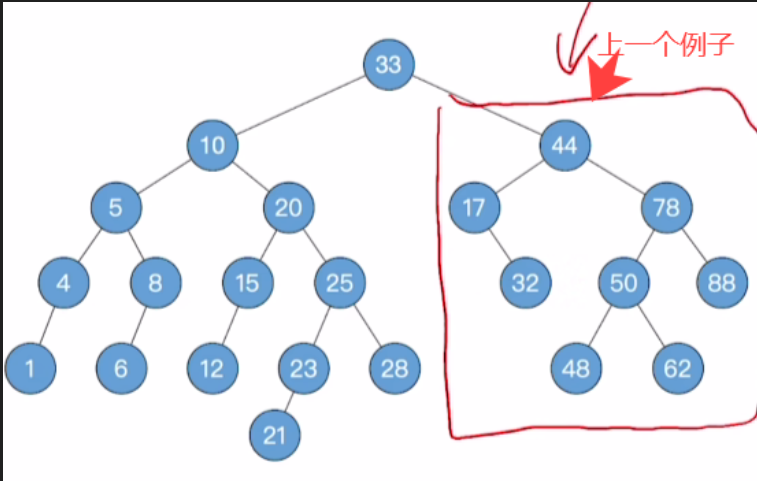
- 由于33的右子树和上一个例子相同,因此我们直接利用上一题的结论,得到下图
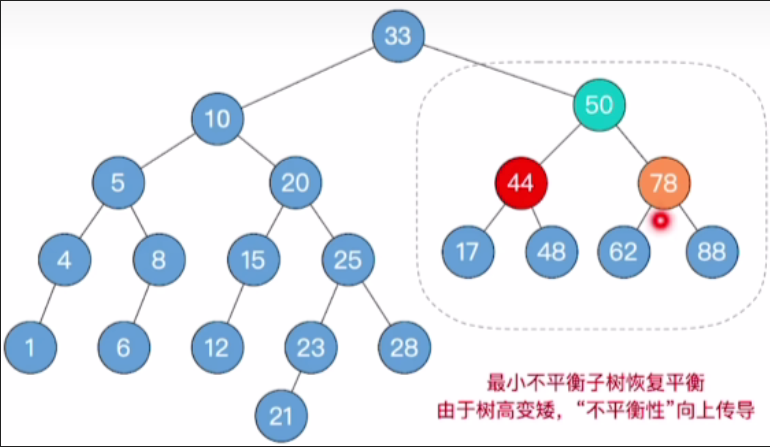
- 此时我们发现33的左子树和右子树的高度相差2,因此发生了"不平衡向上传递"
- 从刚才调整的这颗子树出发,沿着父节点找到最小不平衡子树33,发现其最高的儿子为10,在10这个子树中,最高的孙子是20,此时孙子的类型是LR
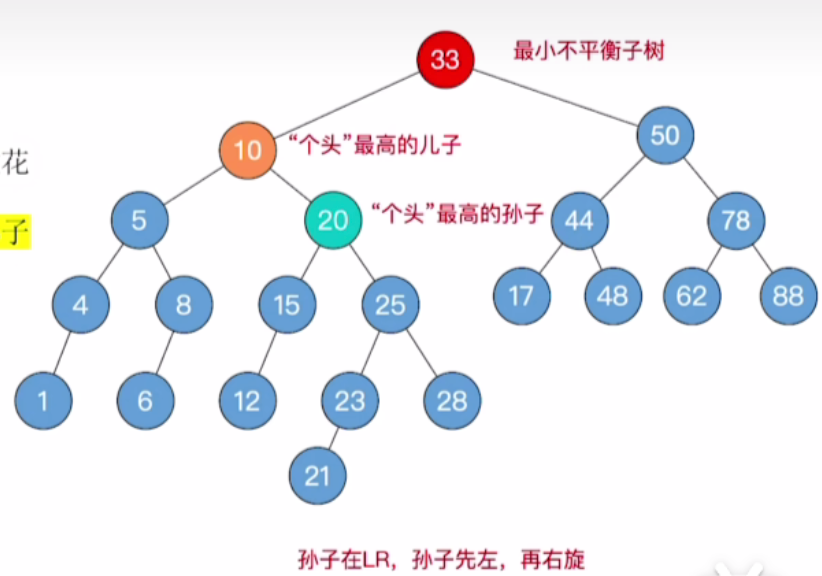
- 因此让孙子20进行先左旋再右旋的双旋操作
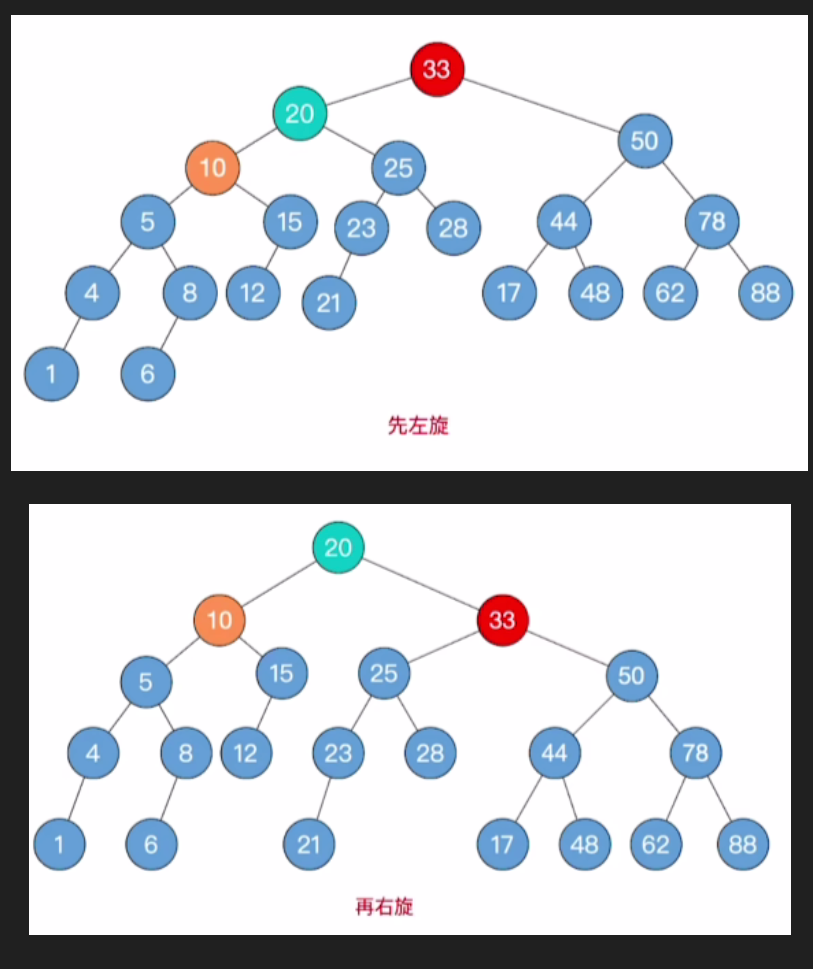
- 那么,此时可以发现二叉树已经平衡,因此操作结束
三.知识回顾与重要考点

结语
四更😉
如果想查看更多章节,请点击:一、数据结构专栏导航页
