当前位置：首页 > news >正文

深度学习中的正交化：理论、应用与实现

news 2025/11/17 8:52:05

摘要：本文系统阐述“正交化”（Orthogonalization）在深度学习中的数学本质、核心作用及典型应用场景。我们将从线性代数基础出发，推导 Gram-Schmidt 正交化过程，介绍正交初始化、正交约束、特征解耦等关键技术，并提供 PyTorch 的完整代码实现。

一、引言：为何需要正交化？

在深度神经网络训练中，我们常面临以下问题：

梯度爆炸/消失：深层网络中梯度逐层放大或衰减；
优化困难：参数空间高度相关，导致损失曲面崎岖；
表示冗余：特征向量之间存在强相关性，降低模型效率。

正交化（Orthogonalization）通过强制权重矩阵或特征向量保持正交性（即相互垂直、无冗余信息），可有效缓解上述问题。

✅ 核心思想：
若权重矩阵 $( W )$ 满足 $( W^\top W = I )$ ，则其列向量构成一组标准正交基，能保持输入信号的范数不变，从而稳定前向传播和反向传播。

二、数学基础：什么是正交化？

2.1 正交向量与正交矩阵

正交向量：两个向量 $( \mathbf{u}, \mathbf{v} \in \mathbb{R}^n )$ 满足

$\mathbf{u}^\top \mathbf{v} = 0$

标准正交基：一组向量 $( {\mathbf{e}_1, ..., \mathbf{e}_k} )$ 满足

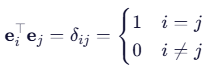
正交矩阵：方阵 $( Q \in \mathbb{R}^{n \times n} )$ 满足

$Q^\top Q = Q Q^\top = I \quad \Rightarrow \quad |Q\mathbf{x}|_2 = |\mathbf{x}|_2$

2.2 Gram-Schmidt 正交化过程

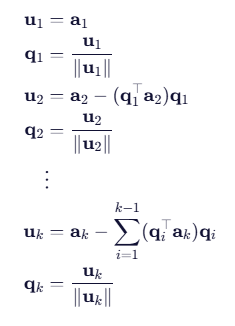
给定线性无关向量组 $( {\mathbf{a}_1, ..., \mathbf{a}_k} )$ ，构造正交基 $( {\mathbf{q}_1, ..., \mathbf{q}_k} )$ ：

💡 该过程将任意基转化为标准正交基，是正交化的经典算法。

三、正交化在深度学习中的三大应用

3.1 正交初始化（Orthogonal Initialization）

动机

Xavier/Glorot 初始化假设激活函数线性，但在 ReLU 等非线性下失效；
正交初始化保证初始权重矩阵为正交矩阵，使信号在前向传播中范数不变。

数学原理

设输入 $( \mathbf{x} \in \mathbb{R}^d )$ ，权重 $( W \in \mathbb{R}^{m \times d} )$ ，若 $( W )$ 正交 $( m = d )$ ，则：

$|W\mathbf{x}|_2 = |\mathbf{x}|_2$

即使 $( m \ne d )$ ，也可通过 SVD 构造近似正交矩阵。

实现方式

对随机矩阵 $( A \in \mathbb{R}^{m \times n} )$ 进行 SVD 分解： $( A = U \Sigma V^\top )$
取 $( W = U V^\top )$ （若 ( m > n )）或 $( W = V U^\top )$ （若 ( m < n )）

3.2 正交约束（Orthogonal Regularization）

动机

训练过程中权重可能偏离正交性；
添加正交惩罚项，鼓励 $( W^\top W \approx I )$ 损失函数设计

$\mathcal{L}{\text{total}} = \mathcal{L}{\text{task}} + \lambda \cdot |W^\top W - I|_F^2$

其中 $( |\cdot|_F )$ 为 $Frobenius$ 范数。

⚠️ 注意：该方法计算开销大，通常用于小规模网络或特定层。

3.3 特征解耦（Disentangled Representation）

动机

学习到的特征应尽可能独立（如人脸图像中：表情、姿态、光照应分离）；
正交性是解耦的一种强形式。

方法

在潜在空间施加正交约束；
使用正交投影层（Orthogonal Projection Layer）。

四、代码实现

4.1 正交初始化（PyTorch）

import torch
import torch.nn as nndef orthogonal_init(layer, gain=1.0):"""对线性层进行正交初始化"""if isinstance(layer, nn.Linear):nn.init.orthogonal_(layer.weight, gain=gain)if layer.bias is not None:nn.init.zeros_(layer.bias)# 示例：构建带正交初始化的网络
class OrthoNet(nn.Module):def __init__(self):super().__init__()self.fc1 = nn.Linear(784, 256)self.fc2 = nn.Linear(256, 128)self.fc3 = nn.Linear(128, 10)# 应用正交初始化orthogonal_init(self.fc1)orthogonal_init(self.fc2)orthogonal_init(self.fc3, gain=1.0)  # 输出层通常不用缩放def forward(self, x):x = torch.relu(self.fc1(x))x = torch.relu(self.fc2(x))return self.fc3(x)

4.2 正交约束（自定义正则化）

def orthogonal_regularization(W, lambda_reg=1e-3):"""计算正交正则化项: ||W^T W - I||_F^2"""m = W.shape[0]  # 输出维度n = W.shape[1]  # 输入维度if m >= n:# W^T W 应接近 I_ntarget = tf.eye(n)gram = tf.matmul(W, W, transpose_a=True)  # W^T Welse:# W W^T 应接近 I_mtarget = tf.eye(m)gram = tf.matmul(W, W)  # W W^Treturn lambda_reg * tf.reduce_sum(tf.square(gram - target))# 在损失函数中使用
loss = task_loss + orthogonal_regularization(W1) + orthogonal_regularization(W2)

4.3 完整训练示例（MNIST + 正交初始化）

import torch
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms# 数据加载
transform = transforms.Compose([transforms.ToTensor()])
trainset = torchvision.datasets.MNIST(root='./data', train=True, download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=128, shuffle=True)# 模型
class Net(nn.Module):def __init__(self):super().__init__()self.fc1 = nn.Linear(784, 512)self.fc2 = nn.Linear(512, 256)self.fc3 = nn.Linear(256, 10)self._initialize_weights()def _initialize_weights(self):for m in self.modules():if isinstance(m, nn.Linear):nn.init.orthogonal_(m.weight)nn.init.zeros_(m.bias)def forward(self, x):x = x.view(-1, 784)x = torch.relu(self.fc1(x))x = torch.relu(self.fc2(x))return self.fc3(x)# 训练
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net().to(device)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)for epoch in range(10):for inputs, labels in trainloader:inputs, labels = inputs.to(device), labels.to(device)optimizer.zero_grad()outputs = model(inputs)loss = criterion(outputs, labels)loss.backward()optimizer.step()print(f'Epoch {epoch+1}, Loss: {loss.item():.4f}')

五、局限性与注意事项

仅适用于全连接层和 RNN：CNN 的卷积核结构不适合直接正交化；
不能完全替代 BatchNorm：BN 解决的是内部协变量偏移，正交化解决的是信号缩放问题；
过强的正交约束可能限制表达能力：需合理设置正则化强度 ( \lambda )。

六、总结

技术	作用	适用场景
正交初始化	稳定初始信号流	全连接网络、RNN
正交约束	训练中维持正交性	小规模网络、生成模型
特征正交化	学习解耦表示	自监督学习、VAE