当前位置：首页 > news >正文

【Java常用API】----- Math

news 2025/11/17 6:34:22

1. Math 类简介

Math 是 Java 中一个非常重要的工具类，用于执行基本的数学运算。它提供了一系列静态方法，方便开发者进行各种数学计算。

特点：

私有化构造方法：不能通过 new 关键字创建 Math 类的对象。
所有方法均为静态：可以直接通过类名调用，如 Math.abs(5)。

2. Math 类的常用方法

以下是 Math 类中常用的静态方法及其说明：

方法名	说明
`public static int abs(int a)`	获取参数的绝对值
`public static double ceil(double a)`	向上取整（进一法）
`public static double floor(double a)`	向下取整（去尾法）
`public static long round(double a)`	四舍五入
`public static int max(int a, int b)`	获取两个整数中的较大值
`public static int min(int a, int b)`	获取两个整数中的较小值
`public static double pow(double a, double b)`	返回 a 的 b 次幂
`public static double random()`	返回一个 [0.0, 1.0) 范围内的随机 double 值

3. 具体方法详解与示例

3.1 `abs()` - 绝对值

Math.abs(x) 方法用于返回参数 x 的绝对值，即去掉符号后的非负数值。它支持多种基本数据类型，包括 int、long、float 和 double。

3.1.1 基本用法示例：

System.out.println(Math.abs(88));        // 输出: 88
System.out.println(Math.abs(-88));       // 输出: 88
System.out.println(Math.abs(-12.34));    // 输出: 12.34

3.1.2 整数溢出问题

在使用 Math.abs(int) 或 Math.abs(long) 时，存在一个容易被忽视的边界问题：
由于 Java 中整数采用补码表示法，负数的取值范围比正数多一个。

以 int 为例：

最小值：Integer.MIN_VALUE = -2147483648
最大值：Integer.MAX_VALUE = 2147483647

❗ 问题来了：+2147483648 超出了 int 的最大表示范围，因此 Math.abs(Integer.MIN_VALUE) 无法表示为正数！

实际表现：

int min = Integer.MIN_VALUE; // -2147483648
System.out.println(Math.abs(min)); // 输出: -2147483648（仍是负数！）

这并不是方法“出错”，而是整数溢出导致的结果未变号，可能引发严重逻辑错误（例如在计算距离、金额等场景）。

3.1.3 解决方案：使用 `Math.absExact()`

从 Java 15 开始，Math 类新增了安全版本的绝对值方法：

方法	功能
`public static int absExact(int a)`	安全计算 `int` 绝对值，若溢出则抛出 `ArithmeticException`
`public static long absExact(long a)`	安全计算 `long` 绝对值，若溢出则抛出 `ArithmeticException`

示例：

try {// 尝试对 Integer.MIN_VALUE（-2147483648）取绝对值// 由于其绝对值 2147483648 超出了 int 类型的最大值（2147483647），// Math.absExact() 会检测到整数溢出并抛出 ArithmeticExceptionint result = Math.absExact(Integer.MIN_VALUE);
} catch (ArithmeticException e) {// 捕获因溢出引发的算术异常，并输出异常的详细消息// e.getMessage() 返回异常构造时传入的描述信息System.out.println("发生溢出：" + e.getMessage());
}

输出结果：

3.2 `ceil()` - 向上取整（进一法）

Math.ceil(double a) 方法用于向上取整，即返回大于或等于参数的最小整数。其本质是向正无穷方向取最接近的整数值。

3.2.1 基本用法示例：

System.out.println(Math.ceil(12.34));   // 输出: 13.0
System.out.println(Math.ceil(12.54));   // 输出: 13.0
System.out.println(Math.ceil(-12.34));  // 输出: -12.0
System.out.println(Math.ceil(-12.54));  // 输出: -12.0

💡 注意：

返回类型为 double，即使结果是整数；
对负数而言，“向上”意味着更靠近零（因为 -12 > -13）。

3.2.2 数轴方向理解

在数轴上，ceil() 总是向右侧（正无穷方向） 移动到最近的整数点：

← 负无穷方向                              正无穷方向 →
... -14   -13   [-12]   -11  ...   12    [13]    14 ...↑_↑                      ↑_↑-12.54 -12.34             12.34 12.54

正数：小数部分无论多小，都进一位；
负数：只要不是整数，就向 0 靠近（数值变大）。

3.3 `floor()` - 向下取整（去尾法）

Math.floor(double a) 方法用于向下取整，即返回小于或等于参数的最大整数。其本质是向负无穷方向取最接近的整数值。

3.3.1 基本用法示例：

System.out.println(Math.floor(12.34));   // 输出: 12.0
System.out.println(Math.floor(12.54));   // 输出: 12.0
System.out.println(Math.floor(-12.34));  // 输出: -13.0
System.out.println(Math.floor(-12.54));  // 输出: -13.0

💡 注意：

返回类型为 double；
对负数而言，“向下”意味着远离零（数值变小）。

3.3.2 数轴方向理解

在数轴上，floor() 总是向左侧（负无穷方向） 移动到最近的整数点：

← 负无穷方向                              正无穷方向 →
... -14   [-13]   -12   -11  ...   [12]    13    14 ...↑_↑                      ↑_↑-12.54 -12.34             12.34 12.54

正数：直接舍去小数部分；
负数：只要不是整数，就向更小的方向取整。

3.4 `round()` - 四舍五入

Math.round() 方法用于执行标准四舍五入运算。Java 提供两个重载版本：

Math.round(float a) → 返回 int
Math.round(double a) → 返回 long

其内部实现原理为：先加 0.5，再向下取整（floor(a + 0.5)）。

3.4.1 基本用法示例：

System.out.println(Math.round(12.54));   // 输出: 13
System.out.println(Math.round(-12.34));  // 输出: -12
System.out.println(Math.round(-12.54));  // 输出: -13

💡 规则说明：

小数部分 ≥ 0.5 → 向绝对值更大的方向进位；
小数部分 < 0.5 → 向绝对值更小的方向舍去；
对负数同样适用，例如 -12.54 的小数部分为 0.54 > 0.5，故结果为 -13。

3.4.2 运算原理图解

以 Math.round(x) 等价于 (long)Math.floor(x + 0.5) 为例：

原值 `x`	`x + 0.5`	`floor(x + 0.5)`	结果
12.54	13.04	13	13
-12.34	-11.84	-12	-12
-12.54	-12.04	-13	-13

⚠️ 特别注意：
Math.round(-12.5) 的结果是 -12，因为 -12.5 + 0.5 = -12.0，floor(-12.0) = -12。

3.5 `pow()` - 幂运算

Math.pow(double a, double b) 方法用于计算 a 的 b 次幂，即 ( a^b )。该方法接受两个 double 类型参数，返回结果也为 double，适用于整数幂、分数幂（如开方）、负指数等多种数学场景。

3.5.1 基本用法示例：

System.out.println(Math.pow(2, 3));      // 输出: 8.0        → 2³ = 8
System.out.println(Math.pow(4, 0.5));    // 输出: 2.0        → √4 = 2（开平方）
System.out.println(Math.pow(2, -2));     // 输出: 0.25       → 2⁻² = 1/4 = 0.25
System.out.println(Math.pow(5, 0));      // 输出: 1.0        → 任何非零数的 0 次方为 1
System.out.println(Math.pow(-2, 3));     // 输出: -8.0       → 负底数奇次幂仍为负

⚠️ 注意：

若底数为负数且指数为非整数（如 Math.pow(-4, 0.5)），结果为 NaN（Not a Number），因为实数范围内无法对负数开偶次方；
所有参数和返回值均为 double，即使传入整数也会自动提升。

3.5.2 精度与性能注意事项

虽然 Math.pow() 功能强大，但在以下情况需谨慎使用：

场景	建议
整数幂运算（如 2³）	对于小整数指数，直接用乘法（如 `2 * 2 * 2`）效率更高、无精度损失
高精度计算	避免用于金融或科学计算，因浮点数存在舍入误差
频繁调用	在性能敏感代码中，可考虑缓存或替换为位运算（如 `1 << n` 表示 2ⁿ）

示例：精度问题

double result = Math.pow(10, 2); // 理论上是 100
System.out.println(result == 100.0); // true// 但某些情况下可能出现微小误差
double r = Math.pow(0.1, 2); // 0.01
System.out.println(r); // 可能输出 0.010000000000000002

3.5.3 相关专用方法（推荐替代）

对于常见的开方操作，Java 提供了更高效、语义更清晰的专用方法：

System.out.println(Math.sqrt(16));   // 开平方根：4.0
System.out.println(Math.cbrt(27));   // 开立方根：3.0

Math.sqrt(x) 等价于 Math.pow(x, 0.5)，但更快且更精确；
Math.cbrt(x) 支持负数（如 cbrt(-8) = -2.0），而 pow(-8, 1.0/3.0) 可能返回 NaN（因 1.0/3.0 是无限循环小数，非精确 1/3）。

✅ 建议：

开平方 → 用 sqrt()；
开立方 → 用 cbrt()；
其他幂运算 → 用 pow()，但注意边界和精度。

3.6 `max()` 和 `min()` - 最大值与最小值

Math.max() 和 Math.min() 用于比较两个数值，并返回其中的较大值或较小值。这两个方法支持多种基本类型（通过重载实现），包括 int、long、float 和 double。

3.6.1 基本用法示例：

// 整数比较
System.out.println(Math.max(20, 30));   // 输出: 30
System.out.println(Math.min(20, 30));   // 输出: 20// 浮点数比较
System.out.println(Math.max(-1.5, -2.3)); // 输出: -1.5
System.out.println(Math.min(3.14, 2.71)); // 输出: 2.71// 特殊值处理
System.out.println(Math.max(Double.NaN, 5.0)); // 输出: NaN
System.out.println(Math.min(Double.POSITIVE_INFINITY, 100)); // 输出: 100.0

说明：

如果任一参数为 NaN，结果为 NaN；
正无穷大（+∞）大于任何有限数；
负零（-0.0）与正零（+0.0）在比较中相等，但 min(+0.0, -0.0) 返回 -0.0（遵循 IEEE 754 标准）。

3.6.2 底层实现与性能

这两个方法内部实现极为简单，以 int 版本为例：

public static int max(int a, int b) {return (a >= b) ? a : b;
}

因此：

无额外开销，可放心在循环或高频逻辑中使用；
不支持三个及以上参数，若需比较多个值，可链式调用：
```
int max = Math.max(Math.max(a, b), c);
```

3.7 `random()` - 随机数生成

Math.random() 是 Java 中最简单、常用的生成伪随机数的方法。它返回一个 大于等于 0.0 且小于 1.0 的 double 类型值，即范围为 [0.0, 1.0)。

该方法内部使用了一个共享的、线程安全的伪随机数生成器（基于 java.util.Random），无需显式创建对象即可调用。

3.7.1 基本用法示例：

// 生成 [0.0, 1.0) 区间的随机 double 值
System.out.println(Math.random()); // 示例输出: 0.345678921345...

特点：

每次调用返回不同的伪随机数（在程序运行期间）；
线程安全，但性能略低于直接使用 Random 实例（因存在同步开销）；
无法设置种子（seed），因此不可复现随机序列。

3.7.2 生成指定范围的随机整数

虽然 Math.random() 返回的是小数，但通过缩放和平移，可轻松生成任意区间的整数。

通用公式：

要生成 [min, max] 范围内的随机整数（包含两端）：

int randomInt = (int) Math.floor(Math.random() * (max - min + 1) + min);

示例：生成 [1, 100] 的随机整数

for (int i = 0; i < 10; i++) {// Math.random() * 100 → [0.0, 100.0)// +1 → [1.0, 101.0)// floor → [1, 100] 的整数long num = (long) Math.floor(Math.random() * 100 + 1);System.out.println(num);
}

输出示例：

⚠️ 注意：

使用 (int) 强转时，若数值超过 Integer.MAX_VALUE 会溢出；
推荐对大范围使用 (long) 或直接采用 java.util.Random。

📌 建议：

在生产环境或需要控制随机性的场景中，优先使用 java.util.Random 或 ThreadLocalRandom；
仅在快速原型、简单测试或教学中使用 Math.random()。

4. 判断质数优化

判断一个数是否为质数（素数）是算法入门中的经典问题。最直观的方法是从 2 开始逐个试除，但这种方法效率较低。通过数学规律的分析，我们可以对算法进行显著优化。

4.1 优化分析

4.1.1 基本思路：质数定义

质数是指大于 1 且只能被 1 和自身整除的自然数。

因此，要判断一个数 n 是否为质数，只需检查是否存在 小于 n 的正整数 d，使得 n % d == 0。

如果存在，则 n 不是质数；否则是质数。

4.1.2 朴素方法的问题（暴力枚举）

for (int i = 2; i < number; i++) {if (number % i == 0) return false;
}
return true;

时间复杂度：O(n)

4.1.3 核心优化：只判断到 √n

数学原理：

如果一个合数 n 有因数 d，那么必然存在另一个因数 n/d。
若 d > √n，则 n/d < √n。

结论：
只要在 [2, √n] 范围内找不到因数，就说明 n 是质数。

示例验证：

数字	平方根	因数对	是否需检查所有数？
16	4	(2,8), (4,4)	只需检查 2~4 即可发现 4 是因数
20	≈4.5	(2,10)	只需检查 2~4，发现 2 整除即可

图解说明：

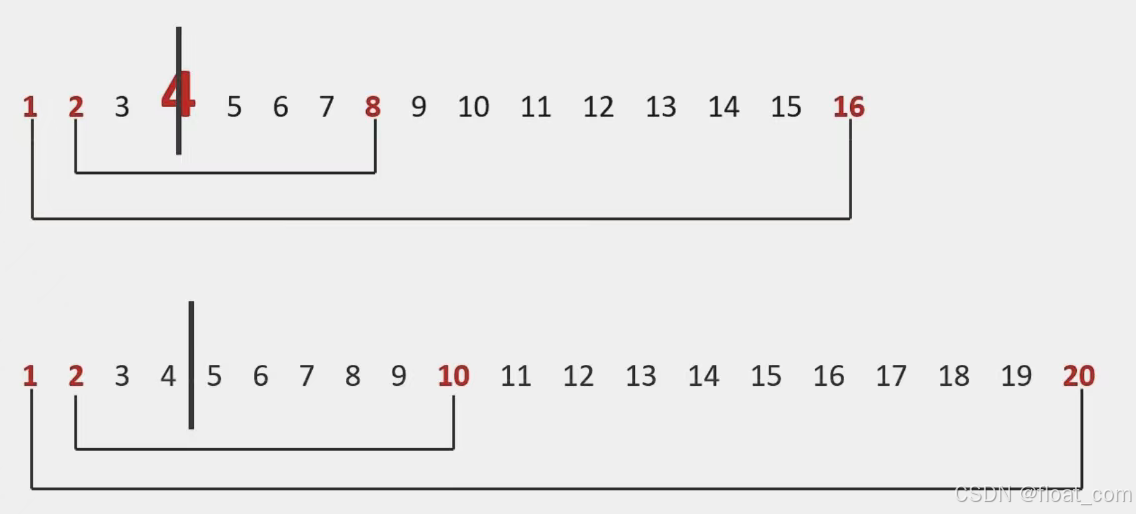
在这里插入图片描述

💡 关键洞察：若 n 有大于 √n 的因数，则必有一个小于等于 √n 的对应因数。

4.1.4 性能对比

方法	循环次数（n=997）	时间复杂度
暴力法（i < n）	995 次	O(n)
优化法（i ≤ √n）	31 次（因为 √997 ≈ 31.6）	O(√n)

优化后性能提升约 30 倍以上！

4.2 完整代码

public class MathDemo2 {public static void main(String[] args) {// 判断一个数是否为质数System.out.println(isPrime(997)); // 输出: true}/*** 判断一个数是否为质数（优化版）* @param number 待判断的数* @return true 表示是质数，false 表示不是*/public static boolean isPrime(int number) {if (number <= 1) return false;int limit =(int)Math.sqrt(number);// 只需检查从 2 到 √numberfor (int i = 2; i <= limit; i++) {if (number % i == 0) {return false;}}return true;}}
}