插值——牛顿插值
插值——牛顿插值
- 插值任务简介
- 插值目标函数
- 牛顿插值原理
- 1. 插值多项式的存在唯一性(回顾)
- 2. 牛顿插值的核心思想:逐步构造
- 3. 差商的定义与递推关系
- 零阶差商:
- 一阶差商:
- 二阶差商:
- 一般 \( k \) 阶差商(递归定义):
- 4. 差商表
- 5. 牛顿插值多项式表达式
- 6. 插值余项(误差公式)
- 7. 牛顿插值的优缺点
- 8. 与拉格朗日插值的对比
- Python 实现
- 结果验证与说明
- 附:文章说明
插值任务简介
与拉格朗日插值一样,牛顿插值(Newton Interpolation) 也是构造一个次数不超过 n n n 的多项式 P n ( x ) P_n(x) Pn(x) 来精确通过所有给定数据点。但它采用了更具结构性和递推优势的表达形式——基于差商(Divided Differences)的基底,使得在新增节点时无需完全重算,且便于程序实现。
本文将介绍牛顿插值的数学原理、构造过程、误差分析,并对比其与拉格朗日插值的异同。
插值目标函数
为便于演示,仍设真实函数为:
f ( x ) = sin x + cos x , x ∈ [ a , b ] f(x) = \sin x + \cos x, \quad x \in [a, b] f(x)=sinx+cosx,x∈[a,b]
在区间 [ a , b ] [a, b] [a,b] 上取 n + 1 n+1 n+1 个互异节点 x 0 , x 1 , … , x n x_0, x_1, \dots, x_n x0,x1,…,xn(可为等距或非等距),对应函数值为 y i = f ( x i ) y_i = f(x_i) yi=f(xi)。
目标:构造一个次数不超过 n n n 的多项式 P n ( x ) P_n(x) Pn(x),使得:
P n ( x i ) = y i , i = 0 , 1 , … , n P_n(x_i) = y_i, \quad i = 0, 1, \dots, n Pn(xi)=yi,i=0,1,…,n
牛顿插值原理
1. 插值多项式的存在唯一性(回顾)
如前所述,给定 n + 1 n+1 n+1 个互异节点及其函数值,存在唯一的次数不超过 n n n 的多项式满足插值条件。因此,牛顿插值与拉格朗日插值本质上构造的是同一个多项式,只是表达形式不同。
2. 牛顿插值的核心思想:逐步构造
牛顿插值采用递增构造的思想:
- 从一个点开始,构造常数插值;
- 增加一个点,添加一次项修正;
- 再增加一个点,添加二次项修正;
- …
- 最终得到 ( n ) 次插值多项式。
关键在于引入差商(Divided Differences作为多项式的系数。
其最终形式为:
P n ( x ) = f [ x 0 ] + f [ x 0 , x 1 ] ( x − x 0 ) + f [ x 0 , x 1 , x 2 ] ( x − x 0 ) ( x − x 1 ) + ⋯ + f [ x 0 , … , x n ] ∏ j = 0 n − 1 ( x − x j ) P_n(x) = f[x_0] + f[x_0,x_1](x - x_0) + f[x_0,x_1,x_2](x - x_0)(x - x_1) + \cdots + f[x_0,\dots,x_n]\prod_{j=0}^{n-1}(x - x_j) Pn(x)=f[x0]+f[x0,x1](x−x0)+f[x0,x1,x2](x−x0)(x−x1)+⋯+f[x0,…,xn]j=0∏n−1(x−xj)
3. 差商的定义与递推关系
零阶差商:
f [ x i ] = f ( x i ) f[x_i] = f(x_i) f[xi]=f(xi)
一阶差商:
f [ x i , x j ] = f [ x j ] − f [ x i ] x j − x i , i ≠ j f[x_i, x_j] = \frac{f[x_j] - f[x_i]}{x_j - x_i}, \quad i \ne j f[xi,xj]=xj−xif[xj]−f[xi],i=j
二阶差商:
f [ x i , x j , x k ] = f [ x j , x k ] − f [ x i , x j ] x k − x i f[x_i, x_j, x_k] = \frac{f[x_j, x_k] - f[x_i, x_j]}{x_k - x_i} f[xi,xj,xk]=xk−xif[xj,xk]−f[xi,xj]
一般 ( k ) 阶差商(递归定义):
f [ x i , x i + 1 , … , x i + k ] = f [ x i + 1 , … , x i + k ] − f [ x i , … , x i + k − 1 ] x i + k − x i f[x_i, x_{i+1}, \dots, x_{i+k}] = \frac{f[x_{i+1}, \dots, x_{i+k}] - f[x_i, \dots, x_{i+k-1}]}{x_{i+k} - x_i} f[xi,xi+1,…,xi+k]=xi+k−xif[xi+1,…,xi+k]−f[xi,…,xi+k−1]
重要性质:差商关于节点对称,即
f [ x i 0 , x i 1 , … , x i k ] = f [ x σ ( i 0 ) , x σ ( i 1 ) , … , x σ ( i k ) ] f[x_{i_0}, x_{i_1}, \dots, x_{i_k}] = f[x_{\sigma(i_0)}, x_{\sigma(i_1)}, \dots, x_{\sigma(i_k)}] f[xi0,xi1,…,xik]=f[xσ(i0),xσ(i1),…,xσ(ik)]
对任意排列 σ \sigma σ 成立。
4. 差商表
以4个点为例,差商可组织为如下三角表:
| x i x_i xi | 零阶 | 一阶 | 二阶 | 三阶 |
|---|---|---|---|---|
| x 0 x_0 x0 | f [ x 0 ] f[x_0] f[x0] | |||
| f [ x 0 , x 1 ] f[x_0,x_1] f[x0,x1] | ||||
| x 1 x_1 x1 | f [ x 1 ] f[x_1] f[x1] | f [ x 0 , x 1 , x 2 ] f[x_0,x_1,x_2] f[x0,x1,x2] | ||
| f [ x 1 , x 2 ] f[x_1,x_2] f[x1,x2] | f [ x 0 , x 1 , x 2 , x 3 ] f[x_0,x_1,x_2,x_3] f[x0,x1,x2,x3] | |||
| x 2 x_2 x2 | f [ x 2 ] f[x_2] f[x2] | f [ x 1 , x 2 , x 3 ] f[x_1,x_2,x_3] f[x1,x2,x3] | ||
| f [ x 2 , x 3 ] f[x_2,x_3] f[x2,x3] | ||||
| x 3 x_3 x3 | f [ x 3 ] f[x_3] f[x3] |
每一列由前一列逐层计算得出,最终第一行的各阶差商即为牛顿插值多项式的系数。
5. 牛顿插值多项式表达式
设已计算出各阶前向差商 f [ x 0 ] , f [ x 0 , x 1 ] , … , f [ x 0 , … , x n ] f[x_0], f[x_0,x_1], \dots, f[x_0,\dots,x_n] f[x0],f[x0,x1],…,f[x0,…,xn],则牛顿插值多项式为:
P n ( x ) = f [ x 0 ] + f [ x 0 , x 1 ] ( x − x 0 ) + f [ x 0 , x 1 , x 2 ] ( x − x 0 ) ( x − x 1 ) + ⋯ + f [ x 0 , … , x n ] ∏ j = 0 n − 1 ( x − x j ) P_n(x) = f[x_0] + f[x_0,x_1](x - x_0) + f[x_0,x_1,x_2](x - x_0)(x - x_1) + \cdots + f[x_0,\dots,x_n]\prod_{j=0}^{n-1}(x - x_j) Pn(x)=f[x0]+f[x0,x1](x−x0)+f[x0,x1,x2](x−x0)(x−x1)+⋯+f[x0,…,xn]j=0∏n−1(x−xj)
或使用求和与乘积符号紧凑表示为:
P n ( x ) = ∑ k = 0 n f [ x 0 , x 1 , … , x k ] ⋅ ∏ j = 0 k − 1 ( x − x j ) P_n(x) = \sum_{k=0}^{n} f[x_0, x_1, \dots, x_k] \cdot \prod_{j=0}^{k-1} (x - x_j) Pn(x)=k=0∑nf[x0,x1,…,xk]⋅j=0∏k−1(x−xj)
(约定当 k = 0 k=0 k=0 时,空乘积为 1)
6. 插值余项(误差公式)
与拉格朗日插值相同,若 f ∈ C n + 1 [ a , b ] f \in C^{n+1}[a,b] f∈Cn+1[a,b],则对任意 x ∈ [ a , b ] x \in [a,b] x∈[a,b],存在 ξ ∈ ( a , b ) \xi \in (a,b) ξ∈(a,b) 使得:
f ( x ) − P n ( x ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ⋅ ( x − x 0 ) ( x − x 1 ) ⋯ ( x − x n ) f(x) - P_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!} \cdot (x - x_0)(x - x_1)\cdots(x - x_n) f(x)−Pn(x)=(n+1)!f(n+1)(ξ)⋅(x−x0)(x−x1)⋯(x−xn)
即余项形式完全一致。误差取决于函数光滑性与节点分布,与插值形式无关。
7. 牛顿插值的优缺点
| 优点 | 缺点 |
|---|---|
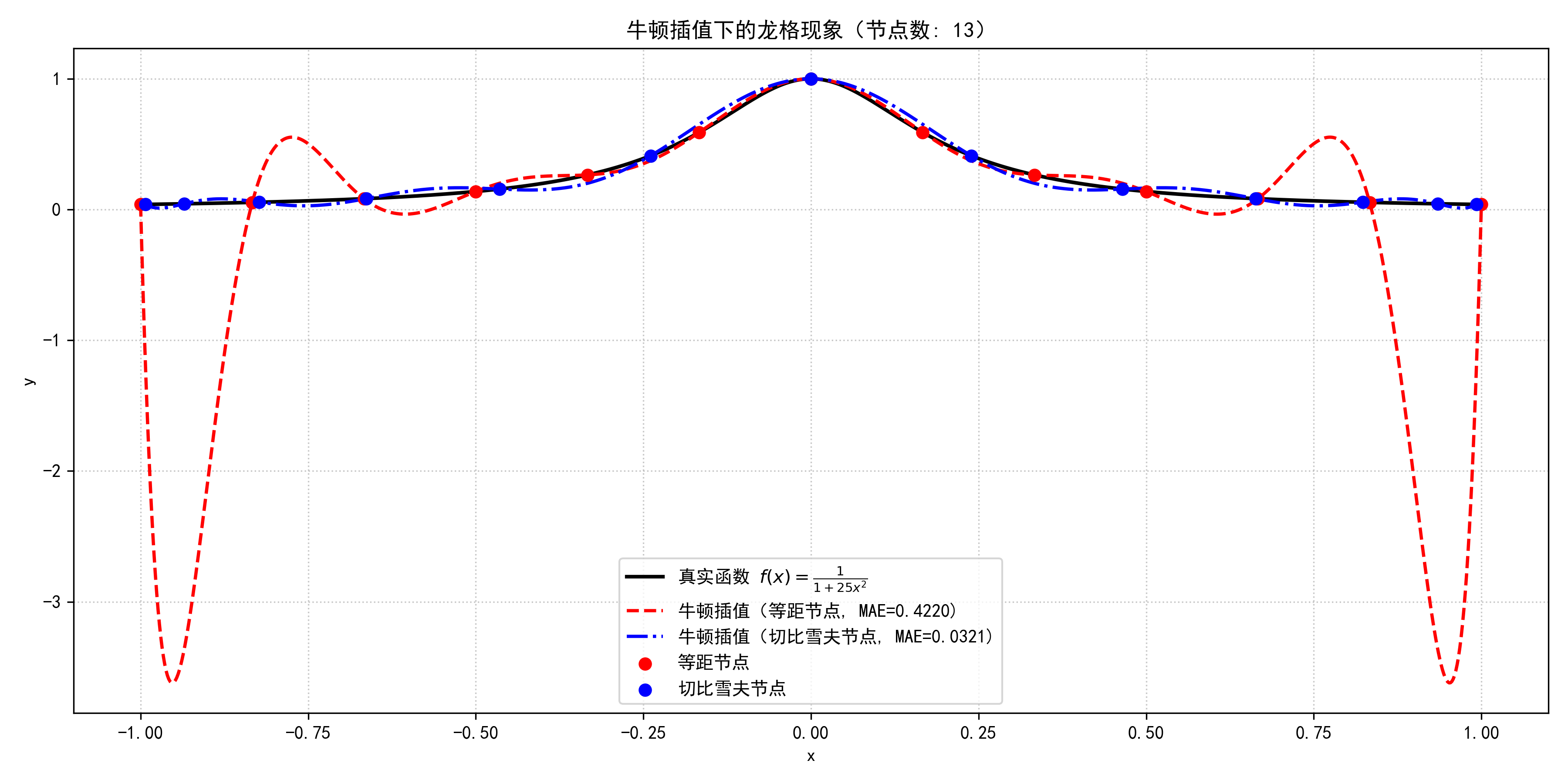
| 递推结构清晰:新增节点只需增加一项,前面积累有效 | 仍为全局多项式:高次时仍可能出现龙格现象 |
| 计算效率高:差商表可动态构建,适合编程 | 对节点顺序敏感 |
8. 与拉格朗日插值的对比
| 特性 | 拉格朗日插值 | 牛顿插值 |
|---|---|---|
| 表达式形式 | 显式基函数求和 | 递推差商展开 |
| 新增节点 | 全部基函数需重算 | 仅需增加最后一项 |
| 适合场景 | 小规模、一次性插值 | 动态插入 |
二者数学等价。
Python 实现
以下代码实现牛顿插值,支持任意节点,并与拉格朗日插值结果验证一致性。
import os
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False# ========== 配置参数 ==========
INTERVAL = (-5.0, 5.0)
N = 10 # 节点数 = N + 1
RESULT_DIR = 输出目录# ========== 目标函数 ==========
def f(x):return np.sin(x) + np.cos(x)# ========== 计算差商表 ==========
def compute_divided_differences(x_nodes, y_nodes):n = len(x_nodes)# 初始化差商表为二维数组dd = np.zeros((n, n))dd[:, 0] = y_nodes # 第0列为函数值(零阶差商)for j in range(1, n): # 列:阶数for i in range(n - j): # 行:起始点dd[i, j] = (dd[i + 1, j - 1] - dd[i, j - 1]) / (x_nodes[i + j] - x_nodes[i])# 返回第一行(即 f[x0], f[x0,x1], ..., f[x0,...,xn])return dd[0, :]# ========== 牛顿插值求值 ==========
def newton_interp(x_nodes, coeffs, x_query):"""coeffs: 牛顿插值系数 = [f[x0], f[x0,x1], ..., f[x0,...,xn]]"""x_query = np.asarray(x_query)n = len(coeffs)result = np.full_like(x_query, coeffs[0], dtype=np.float64)for k in range(1, n):term = coeffs[k]for j in range(k):term *= (x_query - x_nodes[j])result += termreturn result# ========== 主程序 ==========
def main():os.makedirs(RESULT_DIR, exist_ok=True)a, b = INTERVAL# 等距节点x_nodes = np.linspace(a, b, N + 1)y_nodes = f(x_nodes)# 计算牛顿系数(差商)coeffs = compute_divided_differences(x_nodes, y_nodes)# 测试点x_test = np.linspace(a, b, 1000)y_true = f(x_test)y_newton = newton_interp(x_nodes, coeffs, x_test)# 验证:与拉格朗日插值结果是否一致def lagrange_interp(x_nodes, y_nodes, x):x = np.asarray(x)n = len(x_nodes)y = np.zeros_like(x)for k in range(n):Lk = np.ones_like(x)denom = 1.0for j in range(n):if j != k:Lk *= (x - x_nodes[j])denom *= (x_nodes[k] - x_nodes[j])y += y_nodes[k] * (Lk / denom)return yy_lagrange = lagrange_interp(x_nodes, y_nodes, x_test)max_diff = np.max(np.abs(y_newton - y_lagrange))print(f"牛顿插值与拉格朗日插值的最大差异: {max_diff:.2e}")# 计算平均绝对误差 (MAE)mae = np.mean(np.abs(y_newton - y_true))print(f"牛顿插值的平均绝对误差 (MAE): {mae:.6f}")# 绘图plt.figure(figsize=(12, 6))plt.plot(x_test, y_true, 'k-', label=r'真实函数 $f(x) = \sin x + \cos x$')plt.plot(x_test, y_newton, 'b--', label='牛顿插值')plt.scatter(x_nodes, y_nodes, color='red', zorder=5, label='插值节点')plt.grid(True, linestyle=':', alpha=0.7)plt.legend()plt.title(f'牛顿插值(节点数: {N+1})')plt.xlabel('x')plt.ylabel('y')plt.tight_layout()plot_path = os.path.join(RESULT_DIR, 'newton_interp.png')plt.savefig(plot_path, dpi=300)print(f"结果图已保存至: {plot_path}")plt.show()if __name__ == '__main__':main()
结果验证与说明
运行上述代码可得:
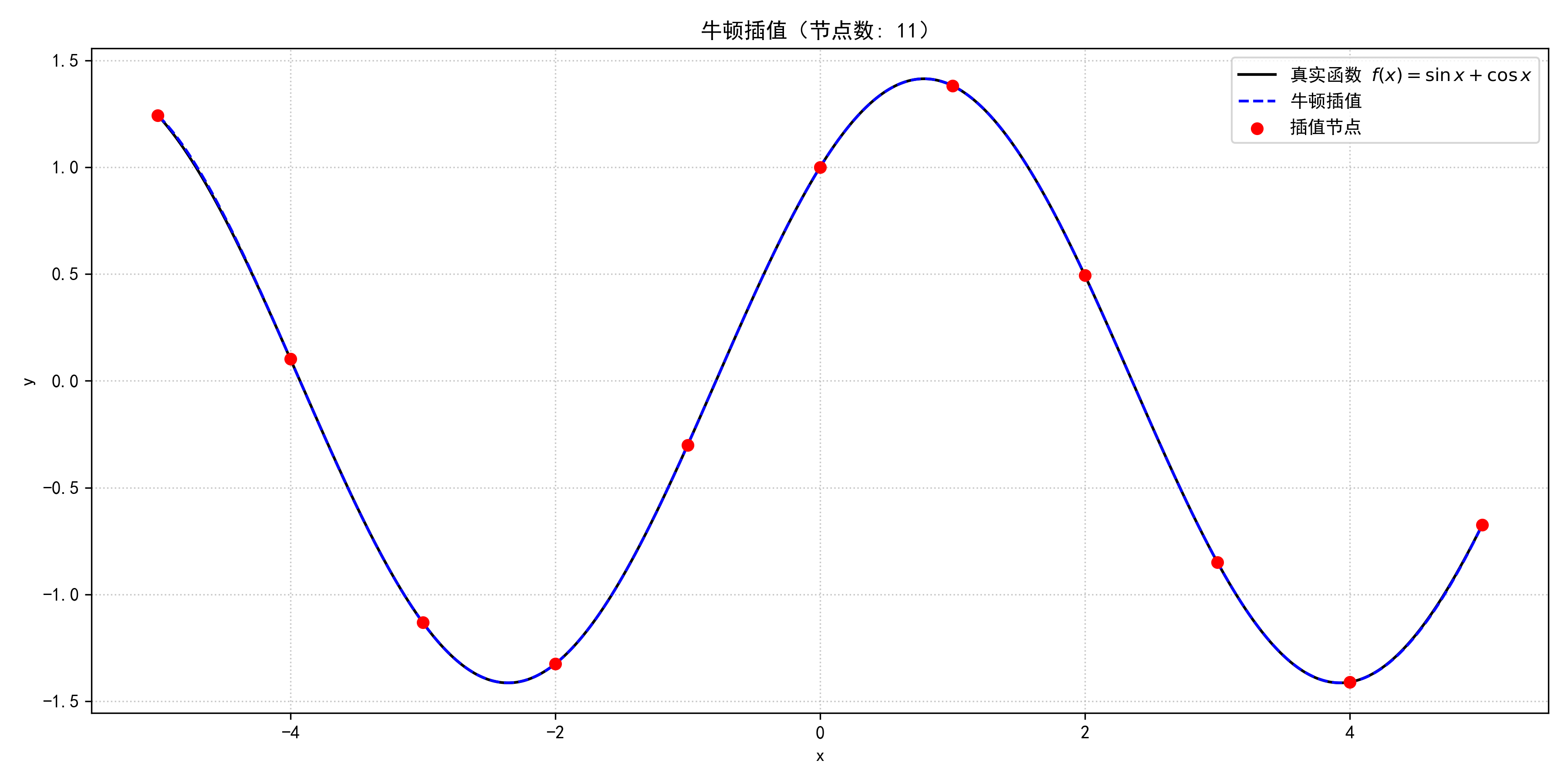
牛顿插值与拉格朗日插值的最大差异: 9.29e-14
牛顿插值的平均绝对误差 (MAE): 0.000889
两种方法计算出的插值结果之差的最大绝对值为: 9.29 × 1 0 − 14 9.29×10^{−14} 9.29×10−14 很小,说明牛顿插值与拉格朗日插值的数值结果一致。
牛顿插值的扩展:
等距节点特例:若 x i = x 0 + i h x_i = x_0 + ih xi=x0+ih,可将差商替换为向前差分,得到牛顿前插公式(Newton Forward Interpolation),适用于表格数据。
附:文章说明
本文仅为个人理解,若有不当之处,欢迎指正~
