模电基础:深度负反馈的放大倍数估算
目录
一、为什么需要引入负反馈?
二、深度负反馈的实质
三、4种组态在深度负反馈时,电压放大倍数的估算
(1)电压串联负反馈
(2)电流串联负反馈
(3)电压并联负反馈
(4)电流并联负反馈
四、总结
一、为什么需要引入负反馈?
在集成运放中,往往会将各种优点汇聚到一起:输入电阻大、输出电阻小,放大倍数极大等等。但这也导致了一些问题,比如想要让其工作在线性区,需要让输入的电压信号在mv甚至更小的级别波动,如果稍大一点就会工作在非线性区而输出恒定值。这反而偏离了我们设计集成运放的目标,于是我们需要将输出量重新引回到输入量的反向端,从而削弱净输入量,最终达到能稳定放大输入电压的范围。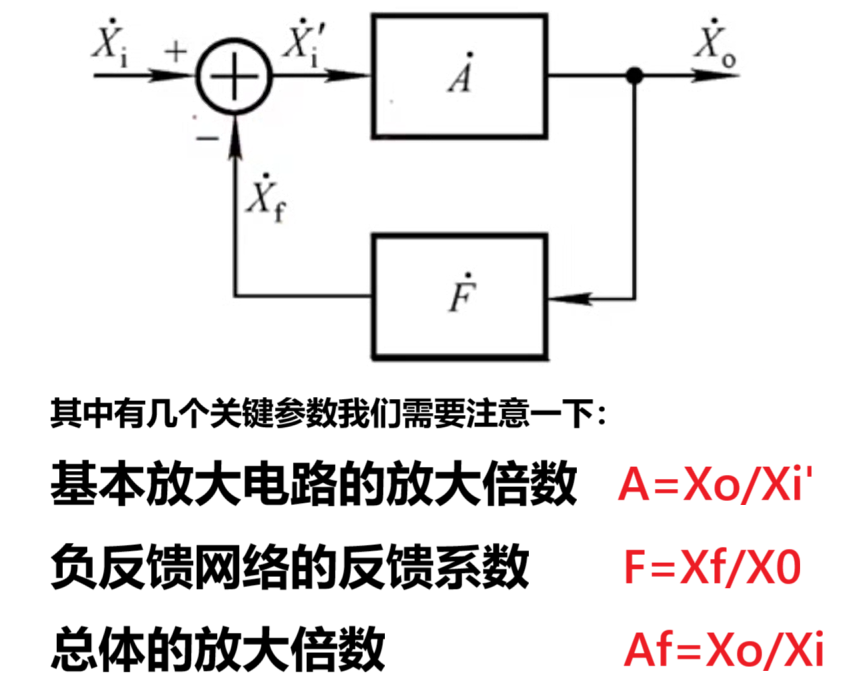
这是一个负反馈的示意图。其中X表示电压或者电流。即对应上篇文章说的4种组态。
他们共有的特点就是输出量比上输入量。额外注意对于反馈网络而言,他的输入量和输出量是相较于基本放大电路相反的。
二、深度负反馈的实质
我们将上述的几个关键参数带入可得: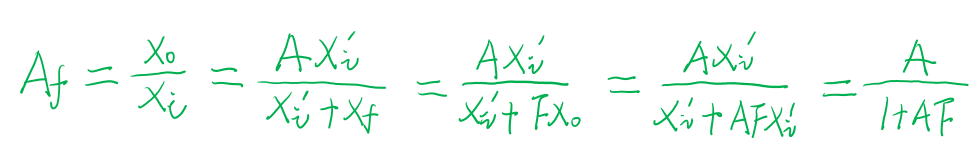
(1)因为我们讨论的是负反馈情况,所以1+AF肯定要大于1,即AF>0。即只有环路增益AF>0时,才是负反馈。
(2)由于集成运放的开环增益A无穷大,总的增益可以化简成1/F。且A越接近无穷大,这个约等号越成立,我们称为深度负反馈。
(3)由于Af=1/F,将原本的表达式Af=Xo/Xi;F=Xf/Xo带入进去可以发现:Xi≈Xf。即在深度负反馈的情况下,净输入量为0,我们称为虚断/虚短。
(4)从式中可以看出,Af、A、F三个变量是同符号的。在以后的计算中可以帮助我们快速化简。
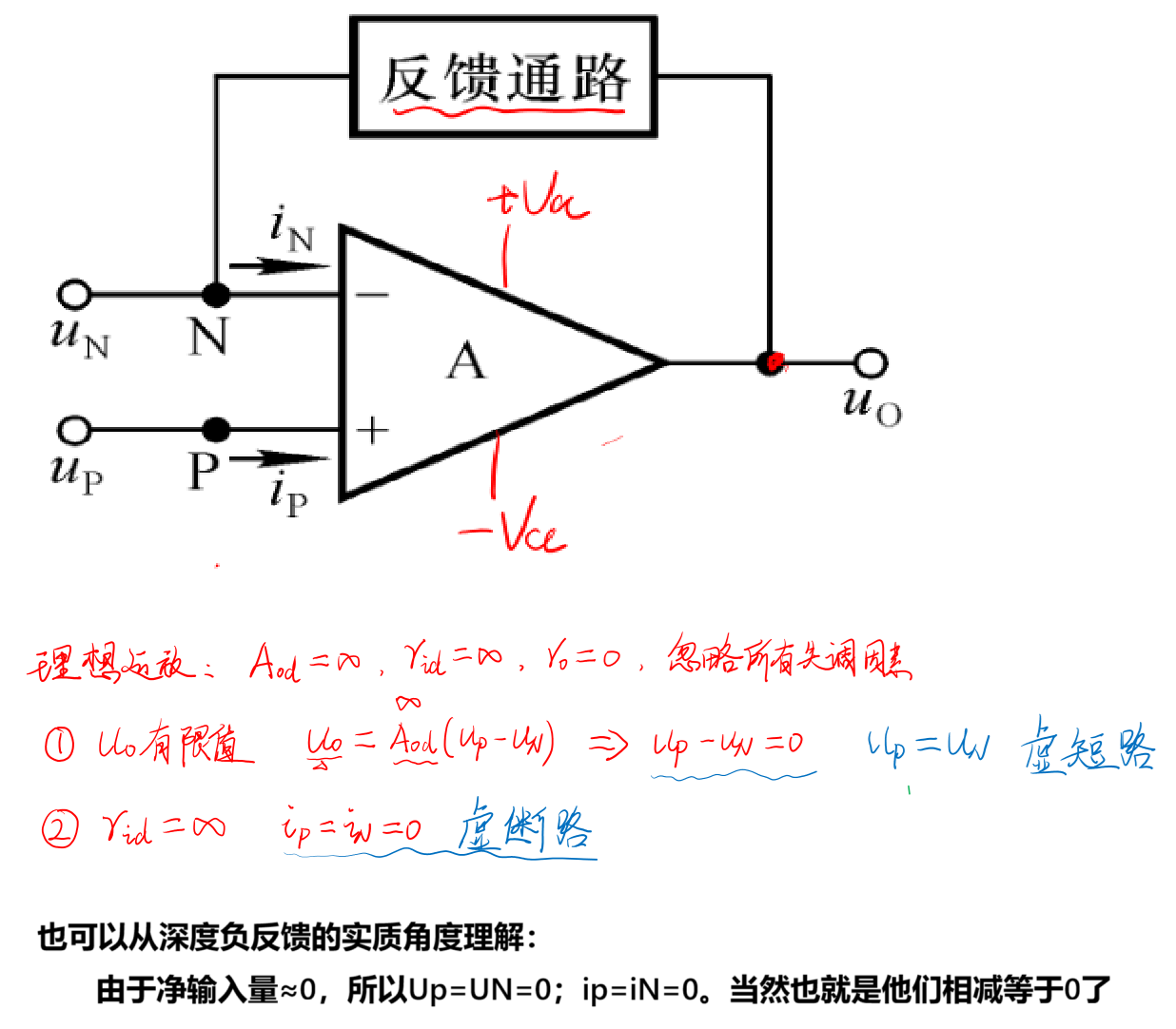
总的来说,深度负反馈的实质就是虚短路和虚断路。在输入量为电压时候,用虚短路来称呼;在输入量为电流的时候,用虚断路来称呼。不过这里说的都是交流角度下,而直流该怎么偏置就怎偏置。
三、4种组态在深度负反馈时,电压放大倍数的估算
(1)电压串联负反馈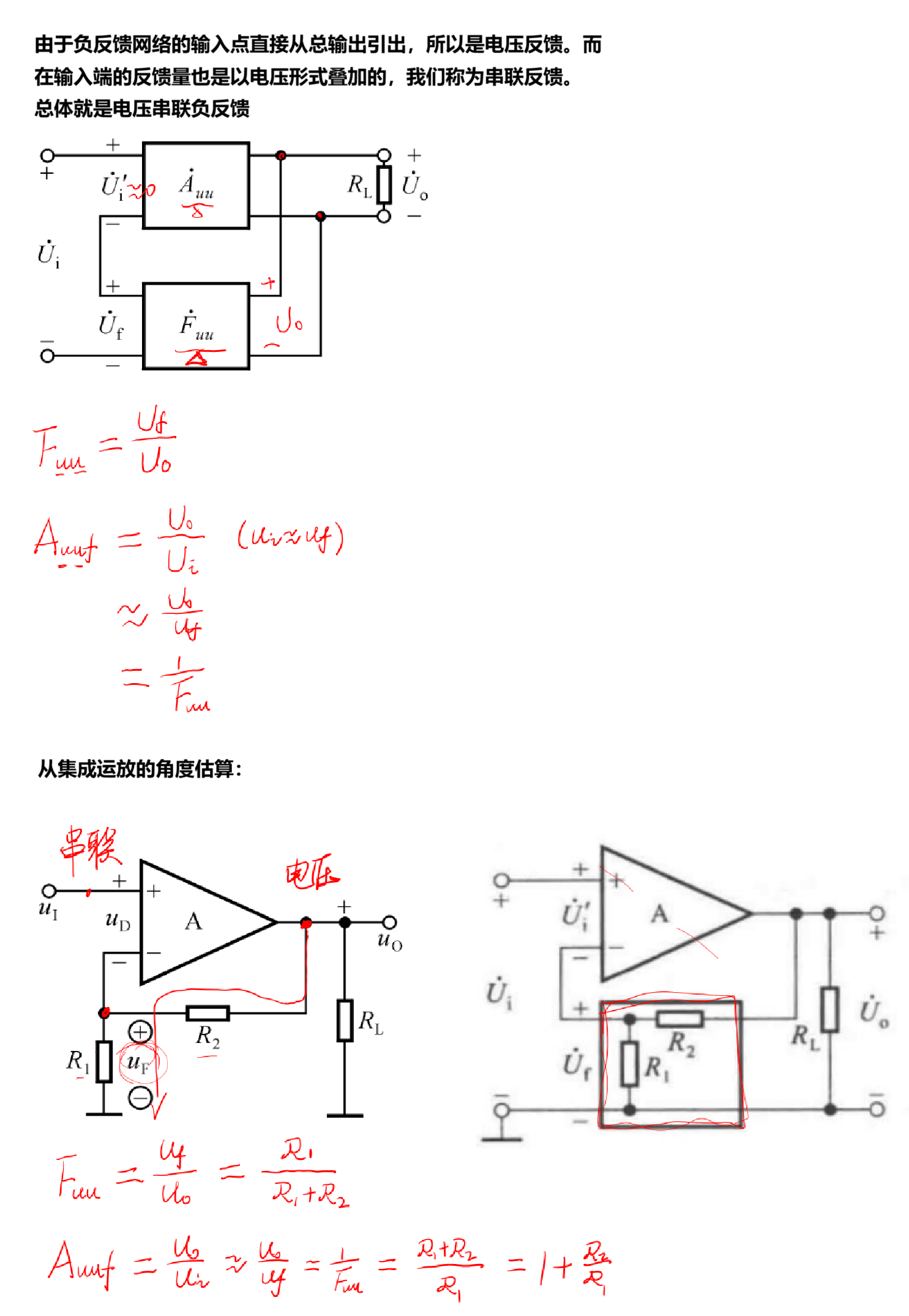
而如果从三极管这种分离元件的角度估算: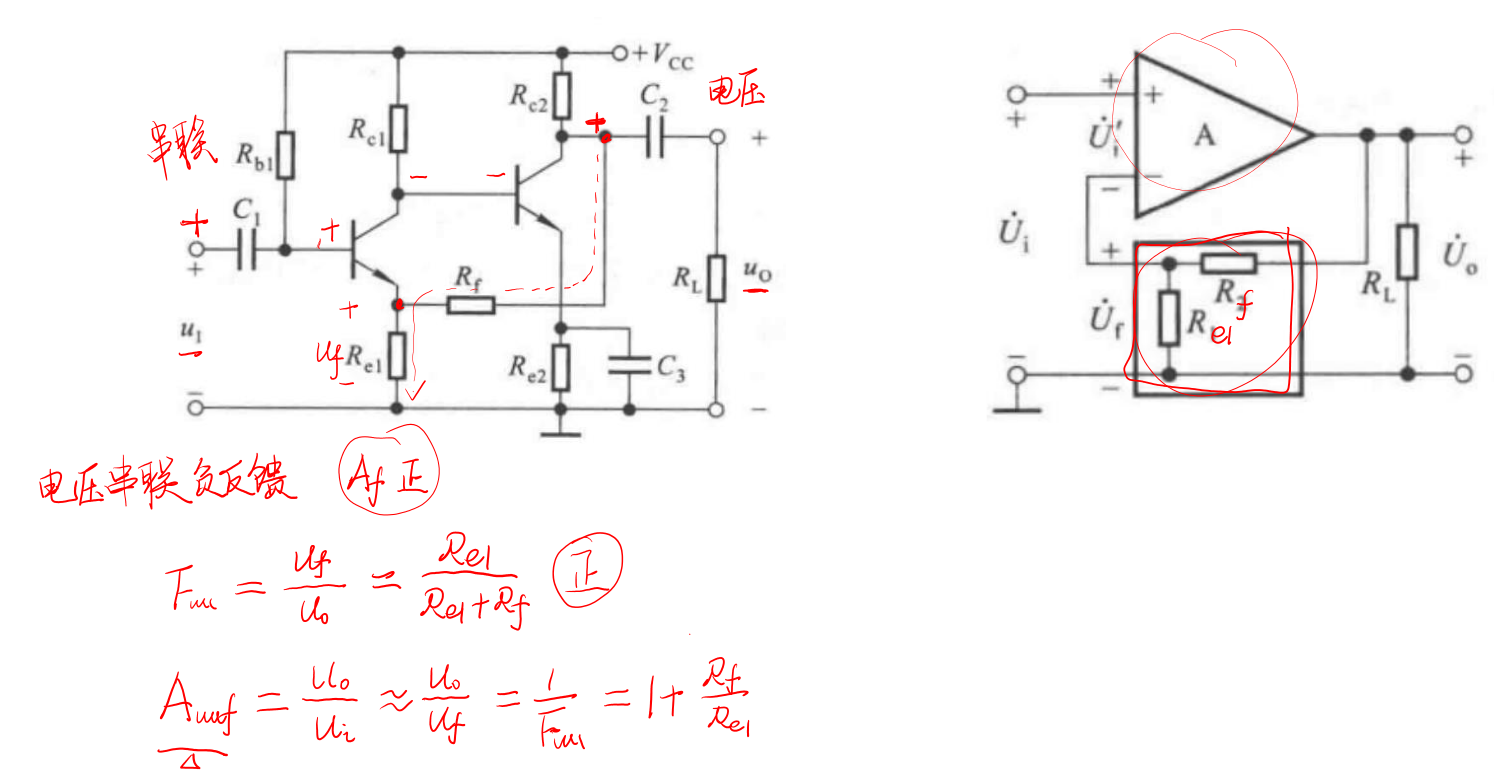
值得注意的就是:虽然此刻变成了分离元件来计算总放大倍数,但前提仍然是工作在深度负反馈条件下,即净输入量=0。在图中体现为Ui≈Uf。
有一个容易理解不正确的点在于,明明三极管工作在放大区需要让Ube≈0.7V左右,但这里又说净输入量≈0,这不是自相矛盾吗?其实是因为整个电路分为直流和交流两个角度,0.7V的压差是在直流条件下偏置得到的,而净输入量≈0是说的交流条件。
(2)电流串联负反馈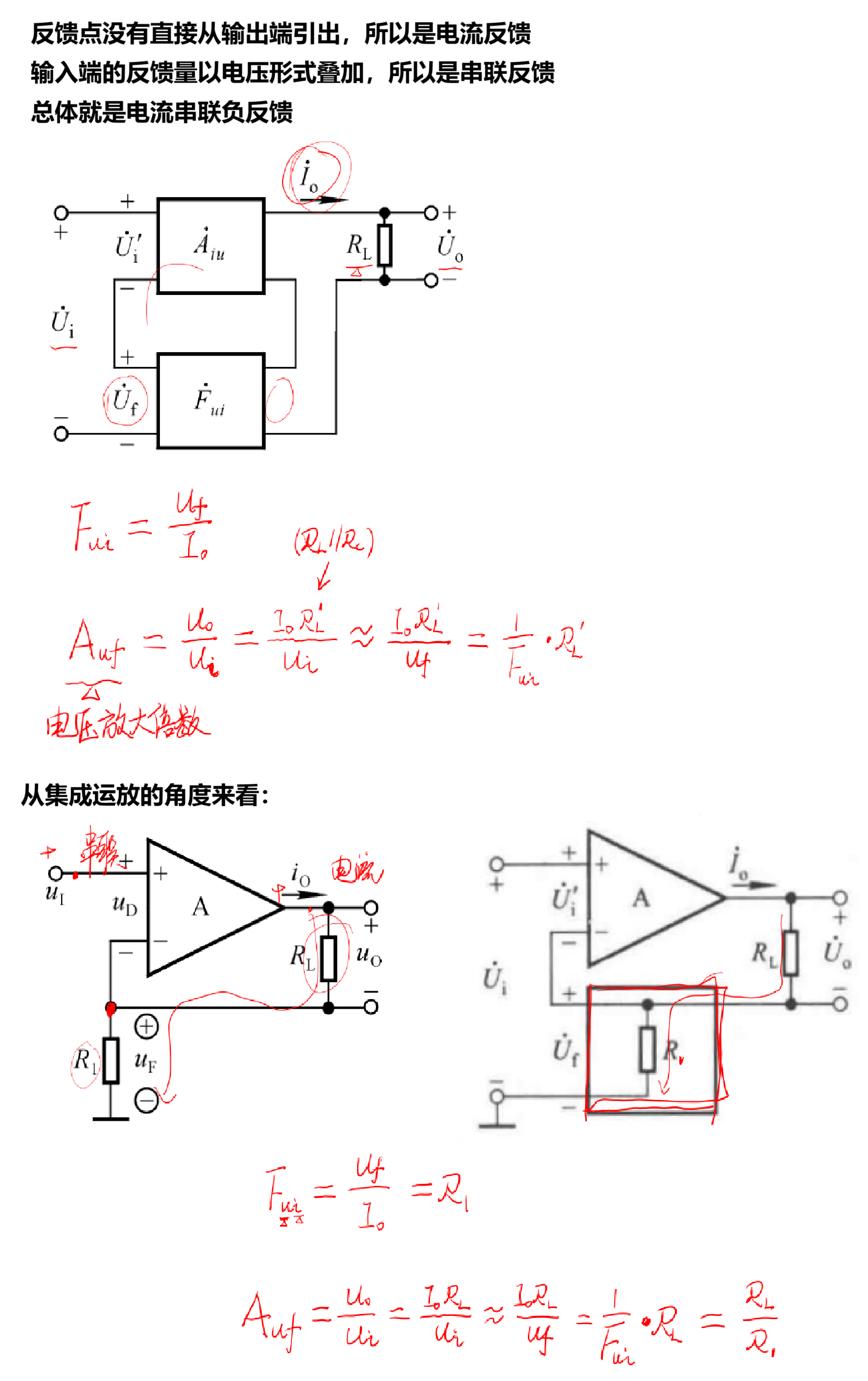
而从分离元件的角度来看: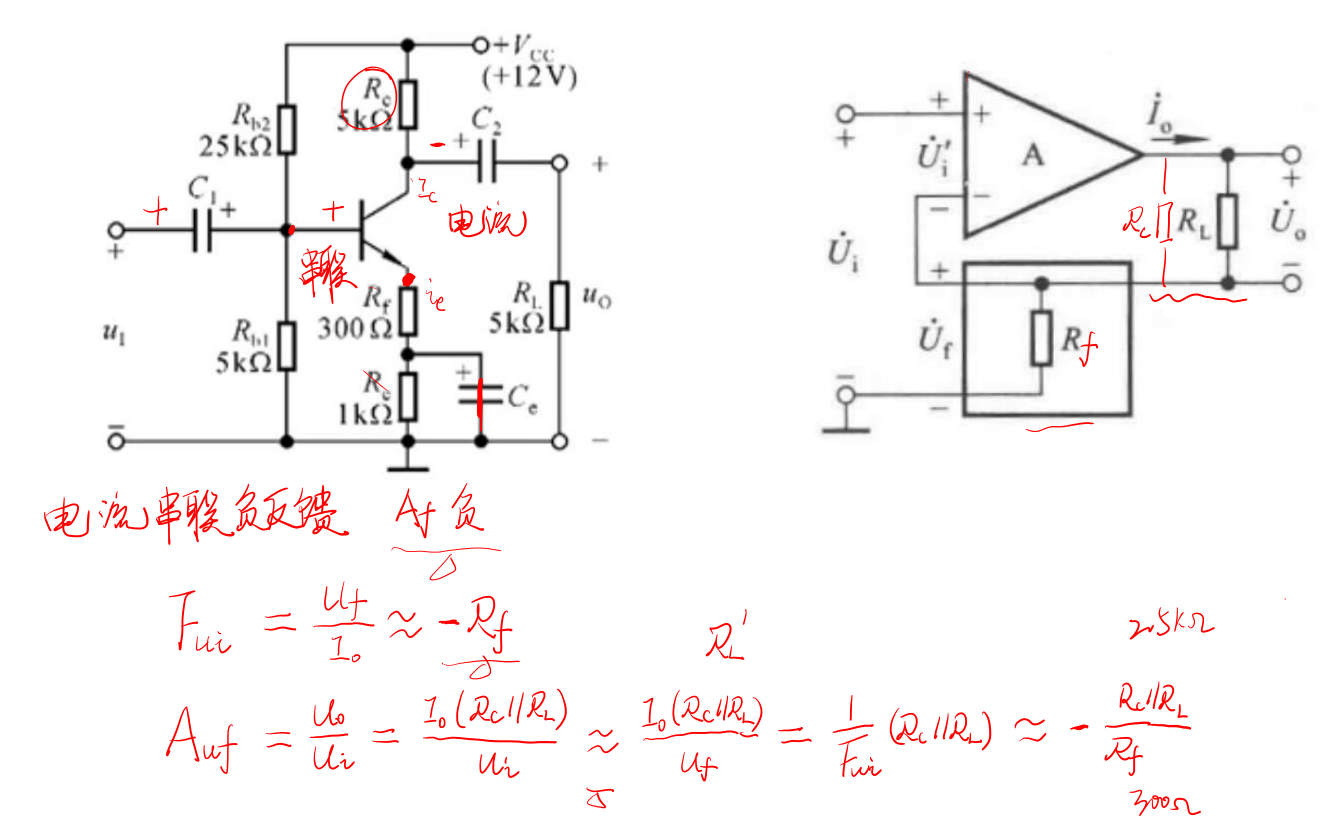
由于我们讨论的都是交流情况下的反馈,所以自然需要将原理图用h参数等效模型画出。即输出端的电流要流经的不再是单独的RL,而是Rc和RL的并联。
下面这个例子也是类似的,只不过反馈网络变得更加复杂,求Uf时候也会变得复杂。不过本质相同的。
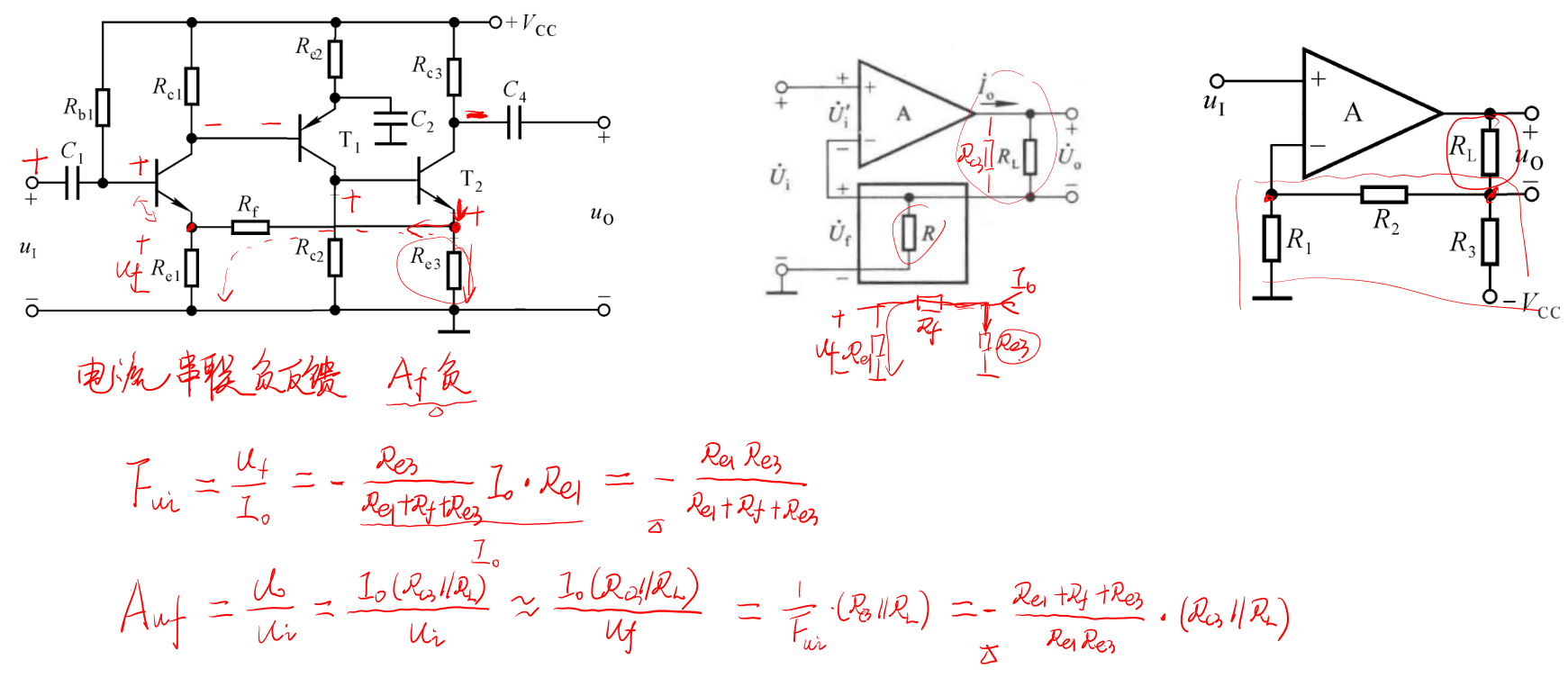
(3)电压并联负反馈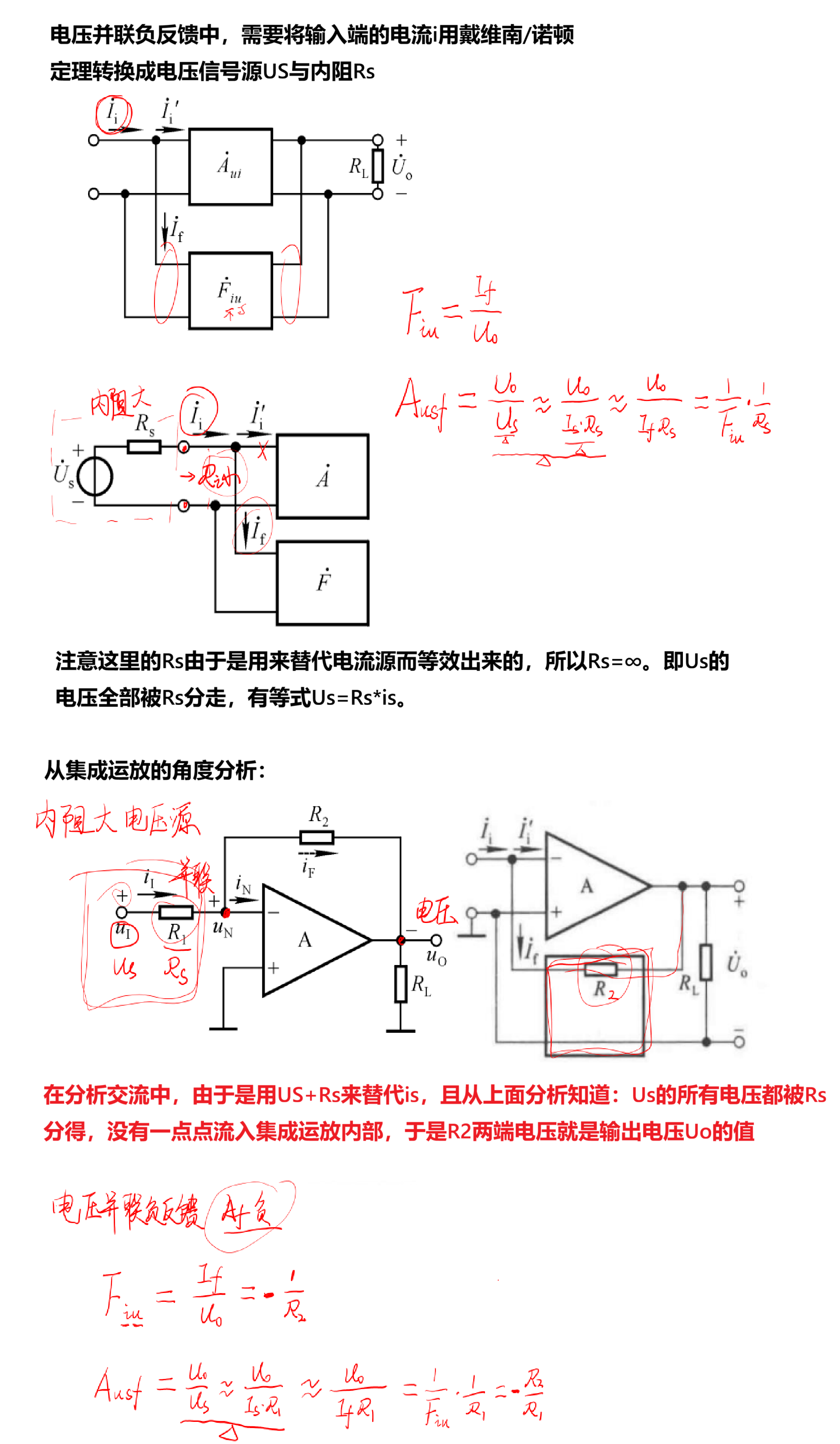
从分离元件的角度考虑: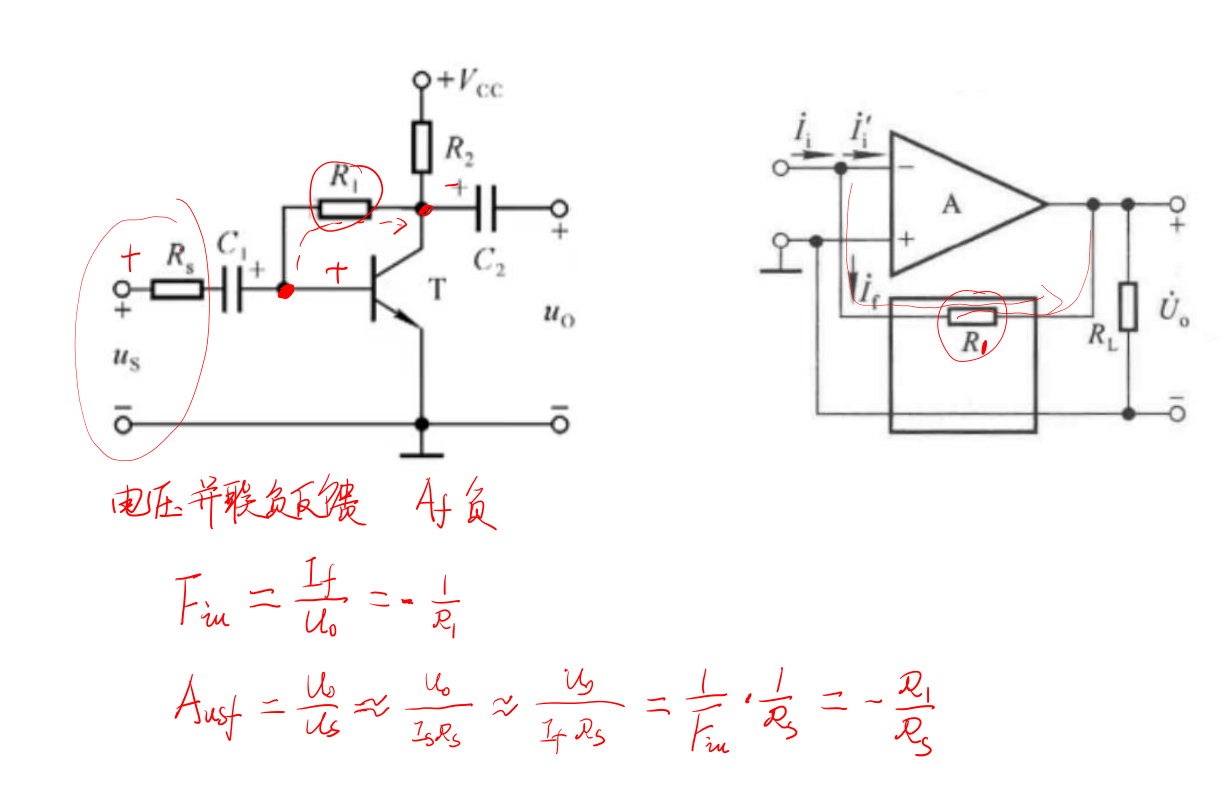
(4)电流并联负反馈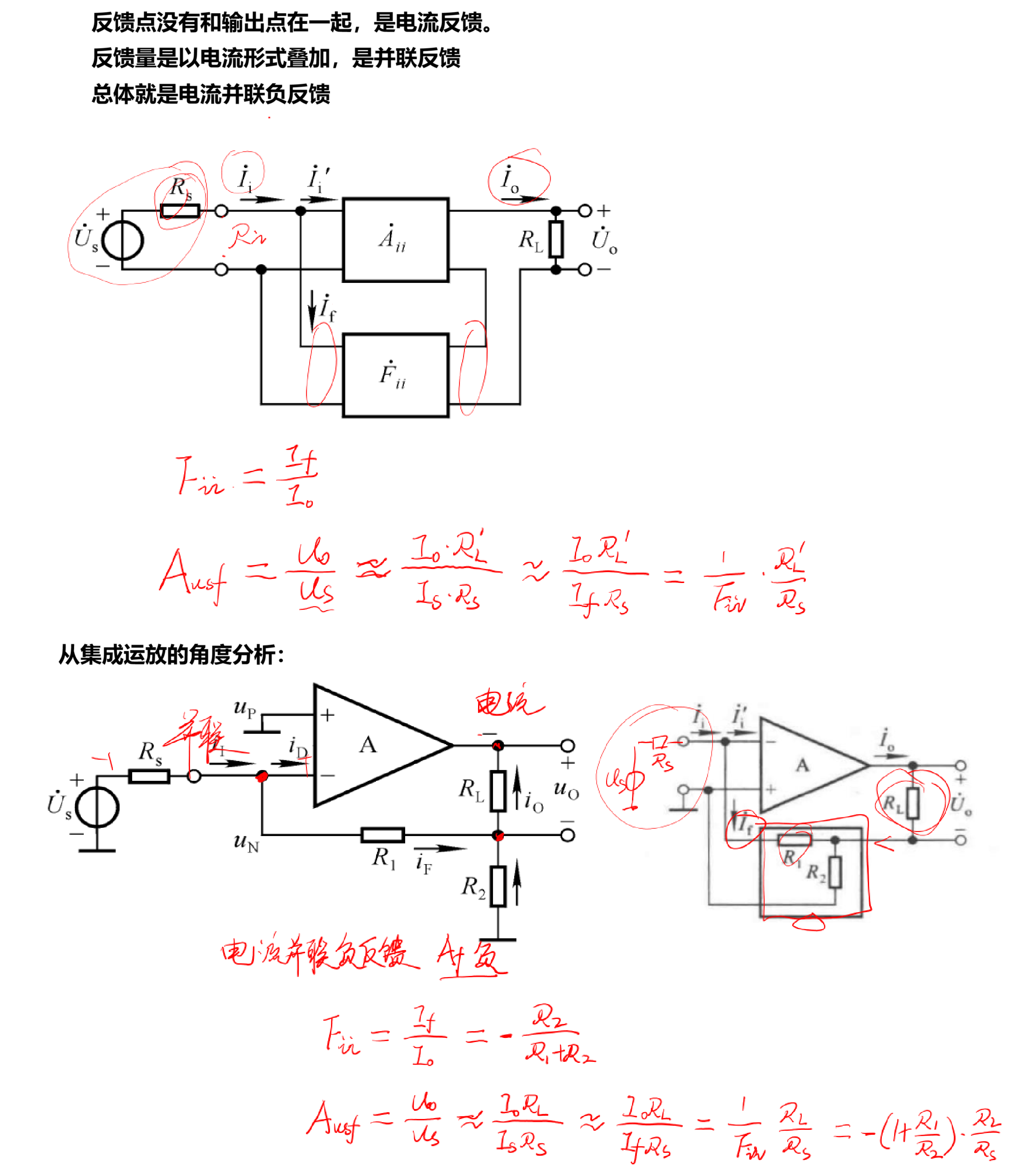
从分离元件的角度考虑: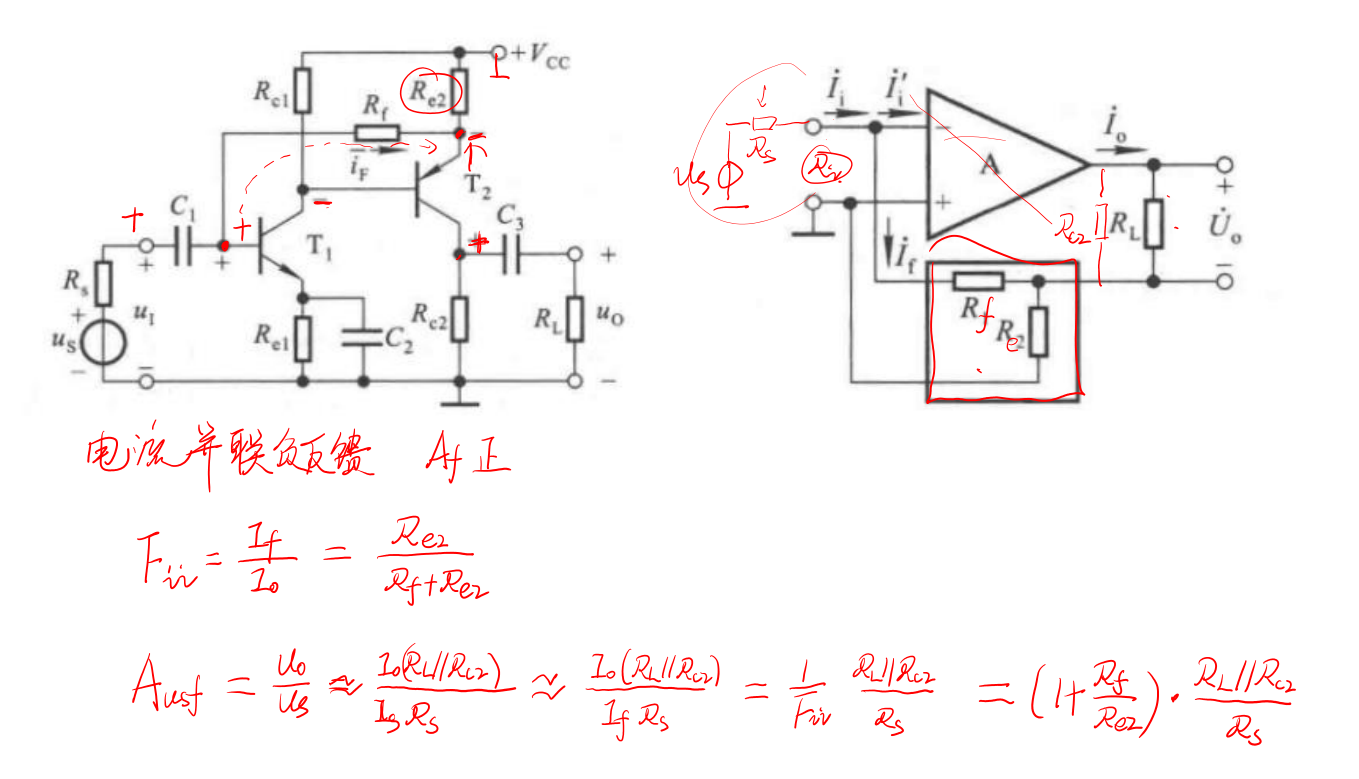
四、总结
对于深度负反馈情况下,要我们求解总的放大倍数Auf。我们需要先分析出他是4种组态中的哪一种,然后根据下标写出F的下标以及表达式。最后用Uo/Ui,并带入F计算出结果。
这整个过程中需要先把分离元件的形式,用简单的集成运放来替代,只标出关键的电阻、电流等属性即可。
关于4种组态的记忆,可以不再从电路图一步步推导,而直接看形式。其中RL和Rs的位置是:RL在外层,Rs与F在一块。(这里是因为输入端电流叠加时,需要用if*Rs来替代Us,而他在分母上,经过1/F颠倒后呈现出F与Rs在一起的特点)
对于电压串联负反馈形式,由于输入端和输出端都是电压形式,所以Auf直接就是1/Fuu
而电流串联负反馈形式,输出端是电流形式,输入端是电压形式叠加,所以Auf=RL*1/Fui
电压并联负反馈形式,输入端是电流叠加,输出端是电压,所以Auf=1/(Fiu*Rs)
电流并联反馈形式,输入端、输出端都是电流,所以Auf=RL*1/(Fii*Rs)
