[学习笔记] An Introduction to Flow Matching and Diffusion Models

arxiv原文
文章翻译

1.介绍

1.1概述

本课程的目标是教你两种最广泛使用的生成式人工智能算法：去噪扩散模型 和 流匹配。所有这些生成模型通过迭代地将噪声 转换为数据来生成对象。从噪声到数据的这种演变是通过模拟常微分或随机微分方程（ODE/SDE）来实现的。
虽然这些讲义是自恰的，但我们鼓励您使用课程网站上的两个资源：讲座录音和实验。

1.2课程结构

第一节：用于采样的生成建模
第二节：流和扩散模型
第三节：构建训练目标
第四节：训练
第五届：条件图像生成

1.3 用于采样的生成模型

图像，视频，分子结构等各种需要生成的数据对象都可以被数学表示为一个向量(可能是展平之后)。因此，我们有:

核心思想1: 生成对象定义为$z\in R^d$。

用于采样的生成: 一张狗的图像可能多种多样，其可能的图像多样性被视为一个概率分布。称为数据分布，表示为$P_{data}$。于是，生成任务可以表示为从未知分布$P_{data}$中采样，即:

核心思想2: 生成一个对象$z$被建模为从数据分布$z\sim P_{data}$中采样。

生成模型是一个机器学习模型，所以我们通常假设可以从$P_{data}$中独立采样有限数量的示例作为真实数据分布的代表，即:

核心思想3: 一个数据集由有限数量的样本$z_1,...,z_N\sim P_{data}$ 组成。

条件生成: 有时，我们希望在某些数据$y$上生成一个有条件的对象。 例如，我们可能希望在y=
“一只狗跑下山坡，山坡上覆盖着雪，背景是山”的条件下生成图像。 我们可以将其改述为从条件分布中抽样：

核心思想4: 条件生成涉及从条件数据分布$z\sim P_{data}(\cdot |y)$中抽样，其中$y$是一个条件变量。

从噪音到数据。生成模型是从$P_{data}$中采样，那么如何采样呢？假设我们可以访问一些初始分布$P_{init}$，从中采样，然后将其转化为来自$P_{data}$的样本。

2.流和扩散模型

可以通过将简单分布$P_{init}$的样本转化为目标分布来实现采样。这种所需的转化可以通过微分方程获得。其中，流匹配对应常微分方程，扩散模型对应随机微分方程。

2.1 流模型

首先定义常微分方程(ODEs)。ODE的解由轨迹(trajectory)定义，其形式为函数:
$$X:[0,1]\to {\mathbb{R}}^d,t\mapsto X_t,$$，即将时间$t$映射到$d$维空间的某个位置向量上。每个ODE都由一个向量场$u$定义，其形式为
$$u:{\mathbb{R}}^d\times [0,1]\to {\mathbb{R}}^d,(x,t)\mapsto u_t(x),$$，即对每个位置$x$和时间$t$，有一个向量$u_t(x)\in R^d$指定空间中的速度。
而常微分方程对轨迹施加一个条件，希望轨迹$X$沿着向量场$u_t$, 从$x_0$出发。这样的轨迹可以形式化为方程的解:
$$\begin{array}{rlrl}\frac{\mathrm{d}}{\mathrm{d}t}{X}_t& =u_t\left(X_t\right)& & >\mathrm{ODE}\\ X_0& =x_0& & >\text{ initial conditions }\end{array}$$
第一个方程定义了常微分方程，要求$X_t$的到导数由$u_t$给出的方向指定。第二个方程指定了初值。所以轨迹是对应一个初值条件下的常微分方程的解。

更一般的问题是: 如果$t=0$时刻, $X_0=x_0$, 在$t$时刻，$X_t$的值是多少。这个问题可以由称为流(flow)的函数回答，它是ODE的解，满足:
$$\begin{array}{rlrl}\psi :{\mathbb{R}}^d\times [0,1]\mapsto {\mathbb{R}}^d,\left(x_0,t\right)\mapsto {\psi }_t\left(x_0\right)& & & \\ \frac{\mathrm{d}}{\mathrm{d}t}{\psi }_t\left(x_0\right)& =u_t\left({\psi }_t\left(x_0\right)\right)& & \text{ flow ODE }\\ {\psi }_0\left(x_0\right)& =x_0& & \text{ flow initial conditions }\end{array}$$

轨迹是常微分方程在给定某个初值对应的一个解。而流是考虑所有初值情况下的函数解。

对于给定初始条件，可以通过流计算出对应的轨迹。向量场、ODE 和流，直观上是同一对象的三个描述：向量场定义了ODEs，它的解是流。一个问题是：解是否存在？若存在是否唯一？

定理3(流的存在唯一性): 如果向量场连续可微且导数有界，则ODE存在且唯一存在一个对应的解-流。这时，对所有$t$，${\psi }_t$是一个微分同胚，即${\psi }_t$连续可微，且有连续可微的反函数。

在机器学习中，流存在唯一性所需要的条件几乎总是得到满足，因为我们使用神经网络来参数化向量场。

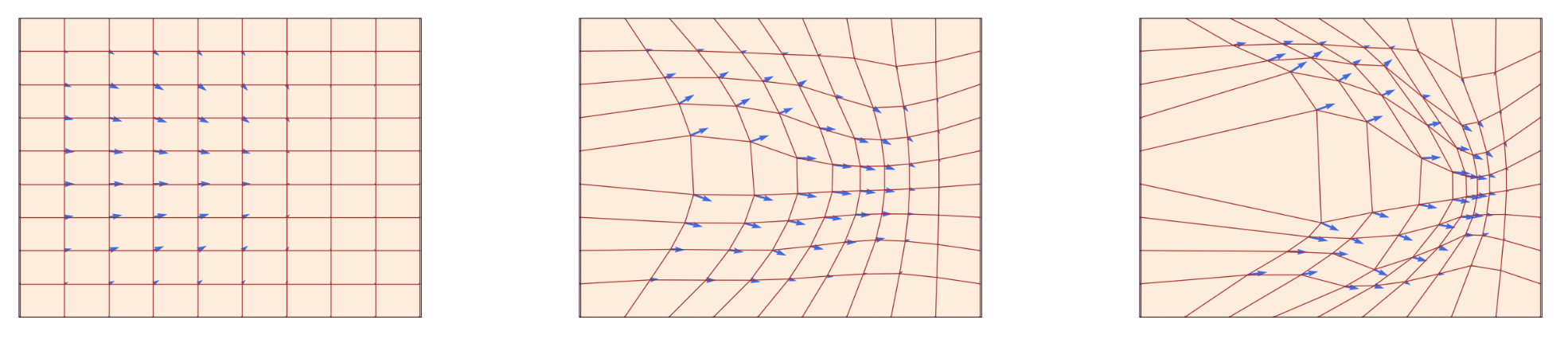
图解: 这是2维空间的水流示例。蓝色箭头表示当时时刻的向量场-速度场。红色线是不同初始条件的水流在某个时刻在不同位置的展示。

例4(线性向量场): 考虑一个简单的线性向量场: $u_t(x)=-\theta x$。 可以证明${\psi }_t(x_0)=exp(-\theta t)x_0$是对应常微分方程的解。

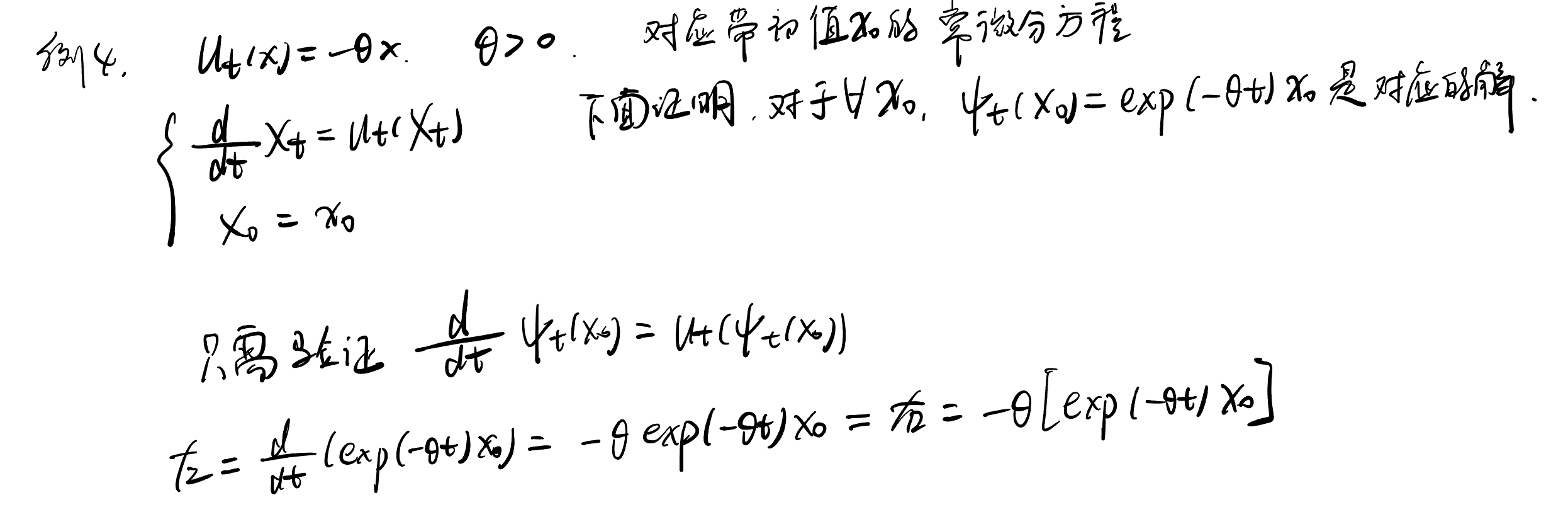
模拟一个ODE: 一般来说，如果向量场函数不简单，那么流 ${\psi }_t$就无法显式计算。这种情况下，人们使用数值方法来模拟计算ODE。其中最简单的是欧拉方法。具体地: 用$X_0=x_0$初始化，并通过以下公式更新:
$$X_{t+h}=X_t+h{u}_t\left(X_t\right)(t=0,h,2h,3h,\dots ,1-h)$$
其中步长$h$是超参数。

本课程，欧拉方法就够用了。更复杂的可以考虑Heun方法。

流模型。我们的目标是将一个简单分布转化为复杂的数据分布。而ODE的模拟是这种转化的自然选择。流模型由ODE描述:
$$\begin{array}{rl}{X}_0& \sim p_{\text{init }}>\text{ random initialization }\\ \frac{\mathrm{d}}{\mathrm{d}t}{X}_t& =u_t^{\theta }\left(X_t\right)>\text{ ODE }\end{array}$$
其中向量场$$\begin{gathered} u_t^{ \\ theta} \end{gathered}$$是一个神经网络，具有参数$\theta$。稍后，我们将讨论神经网络架构的特定选择。我们的目标是使轨迹的终点$X_1$具有分布$P_{d}ata$，即:
$$X_1\sim p_{\text{data }}\iff {\psi }_1^{\theta }\left(X_0\right)\sim p_{\text{data }}$$
尽管被称为流模型，但是神经网络参数化的是向量场而非流。为了计算流，我们需要模拟ODE。
下面的算法总结了如何从流模型中采样的过程：
需求: 确定的向量场(神经网络), 步数
1.t=0
2.计算步长$h=\frac{1}{n}$
3.从$p_{init}$中采样$X_0$
4.利用欧拉方法迭代更新，最终得到$X_1$
5.输出$X_1$作为流模型的采样结果

2.2 扩散模型

随机微分方程(SDEs)通过随机轨迹扩展了来自ODEs的确定性轨迹。随机轨迹通常被称为随机过程$(X_t{)}_{0\le t\le 1}$，并由下面的公式给出：

• 对每个$0\le t\le 1$而言，$X_t$是一个随机变量。
• 对每个$X$而言，$X:[0,1]\to {\mathbb{R}}^d,t\mapsto X_t$是一个随机轨迹

布朗运动。SDEs通过布朗运动构建-这是一个源于对物理扩散过程研究的基本随机过程。一个布朗运动$W=(W_t{)}_{0\le t\le 1}$是一个随机过程，使得$W_0=0$, 轨迹$t\to W_t$是连续的，并且满足下面两个条件:
1.正态增量: 对于[0,t]中的所有$s$, $W_t-W_s\sim \mathcal{N}\left(0,(t-s)I_d\right)$ 即增量具有高斯分布，而方差随着时间线性增加。
2.独立增量: 对于任何 $0\le t_0<t_1<\cdots <t_n=1$ ，增量 $W_{t_1}-W_{t_0},\dots ,W_{t_n}-W_{t_{n-1}}$是独立的随机变量。

设$W_0=0$，步长$h$，并用公式:
$$W_{t+h}=W_t+\sqrt{h}{ϵ}_t,{ϵ}_t\sim \mathcal{N}\left(0,I_d\right)(t=0,h,2h,\dots ,1-h)$$
可以近似模拟一个布朗运动。

从ODEs到SDEs：SDE 的想法是通过添加由布朗运动驱动的随机动力学来扩展 ODE 的确定性动力学。 因为一切都是随机的，我们可能不再像在ODE中那样求导。因此需要找到一个不用导数的ODE等价公式。先重写ODE的轨迹公式，ODE描述轨迹的公式，主要是轨迹关于时间的导数要满足向量场:
$$\frac{\mathrm{d}}{\mathrm{d}t}{X}_t=u_t\left(X_t\right)$$
这个式子可以等价为
$$\frac{1}{h}\left(X_{t+h}-X_t\right)=u_t\left(X_t\right)+R_t(h)$$
也就等价于
$$X_{t+h}=X_t+h{u}_t\left(X_t\right)+h{R}_t(h)$$
也就是一个ODE的轨迹就是在每个时间步朝$u_t\left(X_t\right)$迈出一小步。
现在可以修改最后一个方程使其具有随机性：一个SDE的轨迹${\left(X_t\right)}_{0\le t\le 1}$在每个时间步都朝$u_t\left(X_t\right)$迈出一小步(这个和ODE一样)。但是还要加上来自布朗运动的一些贡献，也就是随机项:
$$X_{t+h}=X_t+\underset{\text{deterministic }}{\underbrace{h{u}_t\left(X_t\right)}}+{\sigma }_t(\underset{\text{stochastic }}{\underbrace{\left(W_{t+h}-W_t\right)}}+\underset{\text{error term }}{\underbrace{h{R}_t(h)}}$$
其中${\sigma }_t$描述了扩散系数，而$R_t(h)$描述了一个随机误差项，也是一个随机变量。它的标准差在h趋于0时，也趋于0。这就是一个随机微分方程。通常也可以用以下符号表示:
$$\begin{array}{rlrl}\mathrm{d}{X}_t& =u_t\left(X_t\right)\mathrm{d}t+{\sigma }_t\mathrm{d}{W}_t& & >\mathrm{SDE}\\ X_0& =x_0& & >\text{ initial condition }\end{array}$$
但这其实是正式公式的非正式表示。此外，SDE不再有flow。这是因为$X_t$的值不再完全由$X_0\sim p_{init}$确定，因为演变本身也是随机的。

在ODE那边，初值确定，轨迹就确定了。所以可以定义以初值和t为自变量的函数-flow。但是这里，即使初值和t作为自变量确定，值也是随机的，所以不存在对应的函数-flow。

但是与ODE相同， 我们有定理:
定理5(SDE解的存在性和唯一性): 如果$u$具有有界导数且连续可微，并且${\sigma }_t$是连续的，那么SDE具有唯一随机过程给出的解。

注意: ODE是SDE的特例。

模拟SDE。类似ODE，SDE可以使用Euler-Maruyama方法进行模拟更新，具体是通过公式:
$$X_{t+h}=X_t+h{u}_t\left(X_t\right)+\sqrt{h}{\sigma }_t{ϵ}_t,{ϵ}_t\sim \mathcal{N}\left(0,I_d\right)$$。

扩散模型。和ODE模型类似，我们可以用SDE构建一个生成模型。具体地，可以参数化一个向量场和扩散系数，构建SDE。而这个SDE是将简单的分布$p_{init}$转化为了一个复杂分布$p_{data}$。
先用$X_0\sim p_{init}$采样，然后通过Euler-Maruyama方法模拟SDE得到轨迹，最后得到t=1时刻的$X_1$。

3.构建训练目标

$u_t^{\theta }$是神经网络，${\sigma }_t$是固定的扩散系数。我们通过最小化损失函数，如均方误差来训练神经网络:
$$\mathcal{L}(\theta )=\Vert u_t^{\theta }(x)-\underset{\text{training target }}{\underbrace{u_t^{\text{target }}(x)}}{\Vert }^2$$
本章我们的目标是找到一个训练目标$u_t^{\theta }$的方程。(先描述ODE情况下，然后推广到SDE)。

3.1 条件和边缘概率路径

第一步: 指定概率路径。

对任意的数$z$，${\delta }_z$称为狄拉克(Dirac)分布，从它中进行采样一定返回$z$。

条件(插值)概率路径的定义: 条件(插值)概率路径是一系列在$R^d$上的分布$p_t(x|z)$，对于所有的$z$而言，它在两端$t=0$和$t=1$满足:
$$p_0(\cdot \mid z)=p_{\text{init }},p_1(\cdot \mid z)={\delta }_z\text{for all z in}{R}^d$$
也就是说，条件概率路径从初始分布逐渐变成单个数据点。

注意, $z$是向量，例如图像数字2，展平之后就是向量$z$。

每个条件概率路径$p_t(x|z)$可以引出一个边缘概率路径$p_t(x)$。
边缘概率路径的定义: 首先从数据分布中抽取一个数据$z\sim p_{data}$，然后从$p_t(\cdot |z)$中采样得到的分布,即:
$$z\sim p_{\text{data }},x\sim p_t(\cdot \mid z)\Rightarrow x\sim p_t$$
$$p_t(x)=\int p_t(x\mid z)p_{\mathrm{data}}(z)\mathrm{d}z$$

两步采样过程，相当于从联合分布$p(x,z)$中采样。
但是如果只看$x$，那就相当于把$z$忽略掉（或者“边缘化”掉），那么$x$的分布就是$$p(x)=\int p(x,z)dz$$
但是无论是联合分布，还是边缘分布。都对应这个采样过程。也就是说，生成一个样本$x$可以等价的看做:
"先从$p_{data}(z)$采样，再从条件分布$p_t(x|z)$采样"或
“直接从边缘分布$p(x)$采样”

注意, 我们知道如何从$p_t$中采样，但是我们不知道密度函数值$p_t(x)$, 因为这个积分很难处理。
下面证明了，在条件概率路径的定义下(也就是条件概率路径满足0时刻时初始分布，t时刻时狄拉克分布)，则边缘概率路径$p_t$插值于$p_{init}$和$p_{data}$，满足: $p_0=p_{\text{init }}$ and $p_1=p_{\text{data }}$ (这被称为噪声-数据插值)
证明: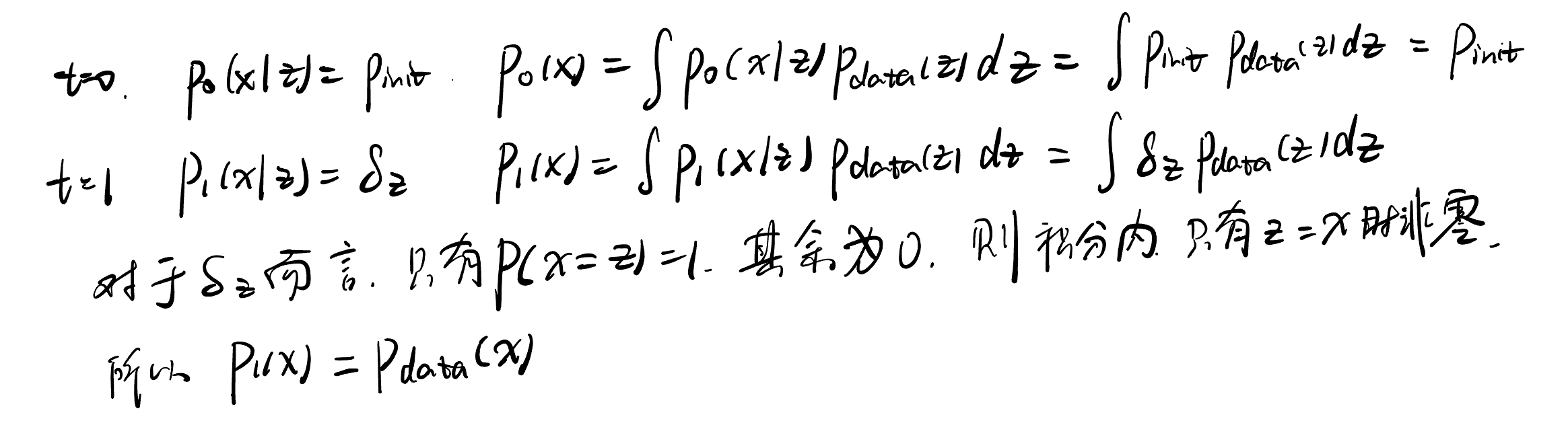

这说明，条件概率路径引出的边缘概率路径，是噪声分布和数据分布之间的插值。

例9(高斯条件概率路径) 这是特别流行的概率路径，也被用于去噪扩散模型。令${\alpha }_t$, ${\beta }_t$为噪声调度器：两个单调可微函数，满足${\alpha }_0={\beta }_1=0$ 和 ${\alpha }_1={\beta }_0=1$ 。然后定义条件概率路径:
$$p_t(\cdot \mid z)=\mathcal{N}\left({\alpha }_{t}z,{\beta }_t^2{I}_d\right)$$
可以验证，它满足条件概率路径的定义:
$p_0(\cdot \mid z)=\mathcal{N}\left({\alpha }_{0}z,{\beta }_0^2{I}_d\right)=\mathcal{N}\left(0,I_d\right),$ and $p_1(\cdot \mid z)=\mathcal{N}\left({\alpha }_{1}z,{\beta }_1^2{I}_d\right)={\delta }_z$
这里用到了方差为0，均值为$z$的正态分布就是${\delta }_z$分布。
这个条件概率路径被称为高斯条件概率路径。
从边缘路径$p_t$中采样可以表示为"先从数据分布采样$z$，然后从$p_t(\cdot \mid z)=\mathcal{N}\left({\alpha }_{t}z,{\beta }_t^2{I}_d\right)$中采样"，即:
$z\sim p_{\text{data }},ϵ\sim p_{\text{init }}=\mathcal{N}\left(0,I_d\right)\Rightarrow x={\alpha }_{t}z+{\beta }_tϵ\sim p_t$
直观上看，当t越小，噪声的占比越大。尤其是t到0的时候，只剩下噪声了。
下图是图5，上面一行展示了条件概率路径，下面一行展示了边缘概率路径。
对于单个数据点，条件概率路径插值了一个高斯分布和狄拉克分布。
边缘概率分布则插值了一个高斯分布和一个数据分布。

3.2 条件和边缘矢量场

现在我们用定义的概率路径$p_t$，为流模型定义一个训练目标$u_t^{\text{target }}$.

定理10(边缘化技巧):
首先给出条件向量场的定义。对于每个数据点$z\in R^d$, 如果$u_t^{\text{target }}(\cdot \mid z)$对应的常微分方程可以产生条件概率路径$p_t(\cdot \mid z)$，则称$u_t^{\text{target }}(\cdot \mid z)$为条件向量场，即:
$$X_0\sim p_{\text{init }},\frac{\mathrm{d}}{\mathrm{d}t}{X}_t=u_t^{\text{target }}\left(X_t\mid z\right)\Rightarrow X_t\sim p_t(\cdot \mid z)(0\le t\le 1)$$

对于每个$z$，我们都有条件向量场可以确定条件概率路径。但我们真正关心的是边缘概率路径。

然后我们定义边缘向量场$u_t^{\text{target }}(x)$为下面的公式:
$$u_t^{\text{target }}(x)=\int u_t^{\text{target }}(x\mid z)\frac{p_t(x\mid z)p_{\text{data }}(z)}{p_t(x)}\mathrm{d}z$$
可以证明，它对应的常微分方程可以产生边缘概率路径，即:
$$X_0\sim p_{\text{init }},\frac{\mathrm{d}}{\mathrm{d}t}{X}_t=u_t^{\text{target }}\left(X_t\right)\Rightarrow X_t\sim p_t(0\le t\le 1)$$特别地，对于这个常微分方程，$X_1\sim p_{data}$， 所以我们说"$u_t^{\text{target }}$将噪声$p_{init}$转化为了数据$p_{data}$"。

在证明之前，我们分析这个定理有什么用: 边缘化技巧允许我们从条件向量场构建边缘向量场。这大大简化了寻找训练目标公式的问题，因为我们通常可以手动找到一个满足定义的条件向量场(通过自己进行代数运算)。下面推导一个关于高斯概率路径的条件向量场进行说明。

示例11(高斯概率路径的目标ODE)

所谓的高斯概率路径，是在整个时间演化过程中，$p_t(x|z)$都是高斯分布。而不是$p_t(x)$都是高斯分布。

证明: 先通过定义构建一个$z$给定下的条件流模型，定义流${\psi }_t^{\mathrm{target}}(x\mid z)$:
$${\psi }_t^{\mathrm{target}}(x\mid z)={\alpha }_{t}z+{\beta }_{t}x$$
如果$X_t$是流${\psi }_t^{\mathrm{target}}(x\mid z)$对应的ODE的轨迹，那么$X_t\sim p_{init}=\mathcal{N}\left(0,I_d\right)$，根据流模型的定义, 有:
$$X_t={\psi }_t^{\mathrm{target}}\left(X_0\mid z\right)={\alpha }_{t}z+\beta t_t{X}_0\sim \mathcal{N}\left({\alpha }_{t}z,{\beta }_t^2{I}_d\right)=p_t(\cdot \mid z)$$
这说明轨迹的分布满足条件概率路径。
接下来，我们可以从条件流中提取条件矢量场。根据流的定义，我们有:

这里第一行x和z是给定的。z表示t=1时刻，对应为z的狄拉克分布。x表示ODE的初值。

(i)使用了我们引入的条件流函数的定义。(ii)重参数化表示了$x$为$\left(x-{\alpha }_{t}z\right)/{\beta }_t$，(iii)重新调整了左边。
最后一个方程就是对应的条件向量场，也就是我们要证明的条件高斯向量场。

这个证明先给出了一个条件流模型，并证明这个流模型可以得到对应的条件概率路径。然后从这个流提取对应的条件向量场。

接下来，我们将通过连续性方程正式证明定理10。为此，我们需要先解释和证明连续性方程。在此之前，先引入散度算子div，它被定义为:
$$\mathrm{div}\left(v_t\right)(x)=\sum _{i=1}^d\frac{\partial }{\partial x_i}{v}_t(x)$$

散度是针对向量场的运算符。可以衡量某个点上流出或者流入该点的量有多少。
向外流 = 正散度，向内流 = 负散度
具体计算是对向量场函数的每个分量单调求偏导，再带入求和

定理12(连续性方程): 考虑一个具有矢量场$u_t^{\text{target }}$ 和 $X_0\sim p_{\text{init }}$的流模型。则$X_t\sim p_t$对所有t成立，当且仅当，对于任何 $x\in {\mathbb{R}}^d,0\le t\le 1$, 有
$${\partial }_t{p}_t(x)=-\mathrm{div}\left(p_t{u}_t^{\text{target }}\right)(x)$$其中${\partial }_t{p}_t(x)=\frac{\mathrm{d}}{\mathrm{d}t}{p}_t(x)$ 表示 $p_t(x)$ 的时间导数。

这个证明的略。详细可以看附录B。

直观理解连续性方程: 左侧表示概率$p_t(x)$在$x$随着时间的变化，这种变化对应于概率质量的净流入。
而对于一个流动模型，描述了一个粒子$X_t$沿着矢量场$u_t^{\text{target }}$运动。散度衡量了矢量场的某种净流出量(散度为正表示向外流)。

下面的笔记参考: https://www.bilibili.com/video/BV1ePYdeWEee
这个笔记证明了质量守恒的连续性方程。
先看看质量守恒的连续性方程。
简单来说，考察有限控制体。由于其在空间中的位置不变，以及质量守恒定理。于是有:
一.从质量角度出发，质量变化=质量增加(减少)=$\frac{\partial \rho }{\partial t}dxdydz$
二.从质量流量(体积流量表示单位时间通过某个截面的体积，质量流量还需要乘以密度)角度出发，各方向单位流出:
以x方向为例。流出质量-流入质量=$\frac{\partial (\rho u)}{\partial x}dxdydz$, 其中$u$是x方向的流速
y方向: 流出质量-流入质量=$\frac{\partial (\rho v)}{\partial y}dxdydz$, 其中$v$是y方向的流速
z方向: 流出质量-流入质量=$\frac{\partial (\rho w)}{\partial z}dxdydz$, 其中$w$是z方向的流速
汇总有总流出=$\frac{\partial (\rho u)}{\partial x}dxdydz+\frac{\partial (\rho v)}{\partial y}dxdydz+\frac{\partial (\rho w)}{\partial z}dxdydz$，这就是$div(\rho V)dxdydz$, 这里$V=u\cdot i+v\cdot j+w\cdot k$是流速向量场。
三.我们知道，2中对应的流出质量-流入质量。1中对应的是质量变化。根据质量守恒: 一个封闭系统的总质量不会凭空消失或者出现。所以1中产生的质量增加(减少)一定对应2中的质量流入(流出)。所以数值的绝对值上两者相等。
然后2中，流出为正，流入为负。1中，流入为正，流出为负。所以两者符号相反。因此有
$$\frac{\partial \rho }{\partial t}=-div(\rho \cdot V)$$
这是质量守恒的连续性方程，我们可以推广到概率守恒的连续性方程。
将质量密度$\rho (x,y,z,t)$改成概率密度$p(x,y,z,t)$(或者统一用x表示x,y,z，就是$p(x,t)$, 或$p_t(x)$)。将流速向量场$V$改成向量场$u_t^{\text{target }}$。由于概率质量也是守恒的(系统的总概率始终为1，概率不会无故产生或者消失。它只能从一个区域流向另一个区域，也就是概率质量只是在空间中重新分布)。所以仍然有连续性方程。也就是概率守恒的连续性方程是对的。

下面继续证明边缘化技巧。
证明: 根据概率的连续性方程。我们只需要证明我们定义的边缘向量场:
$$u_t^{\text{target }}(x)=\int u_t^{\text{target }}(x\mid z)\frac{p_t(x\mid z)p_{\text{data }}(z)}{p_t(x)}\mathrm{d}z$$它满足连续性方程，那么由它对应的ODE得到的轨迹就服从边缘概率路径，即:
$$X_0\sim p_{\text{init }},\frac{\mathrm{d}}{\mathrm{d}t}{X}_t=u_t^{\text{target }}\left(X_t\right)\Rightarrow X_t\sim p_t(0\le t\le 1)$$.
我们直接计算它是否满足连续性方程。

(i)使用了$p_t(x)$的定义，它是从联合分布中采样得到的，所以可以通过联合分布边缘化计算。
由于$p_t(\cdot \mid z)$是条件概率路径，所以在(ii)中我们使用了条件概率路径的连续性方程，即概率密度的时间导数等于负的概率密度和向量场乘积的散度。
对于(iii)，由于散度算子本质上是先逐分量关于x,y,z求偏导，再进行累加求和。而积分是关于z进行积分，所以可以交换顺序。提到最外面。
对于(iv)，我们从积分里面提出了与z无关的$p_t(x)$
最后, 我们证明了$u_t^{\text{target }}(x)$满足连续性方程。根据定理，对应ODE的轨迹$X_t$服从边缘概率路径。

现在我们回看定理10的说明图(下图)。这是用常微分方程模拟概率路径。

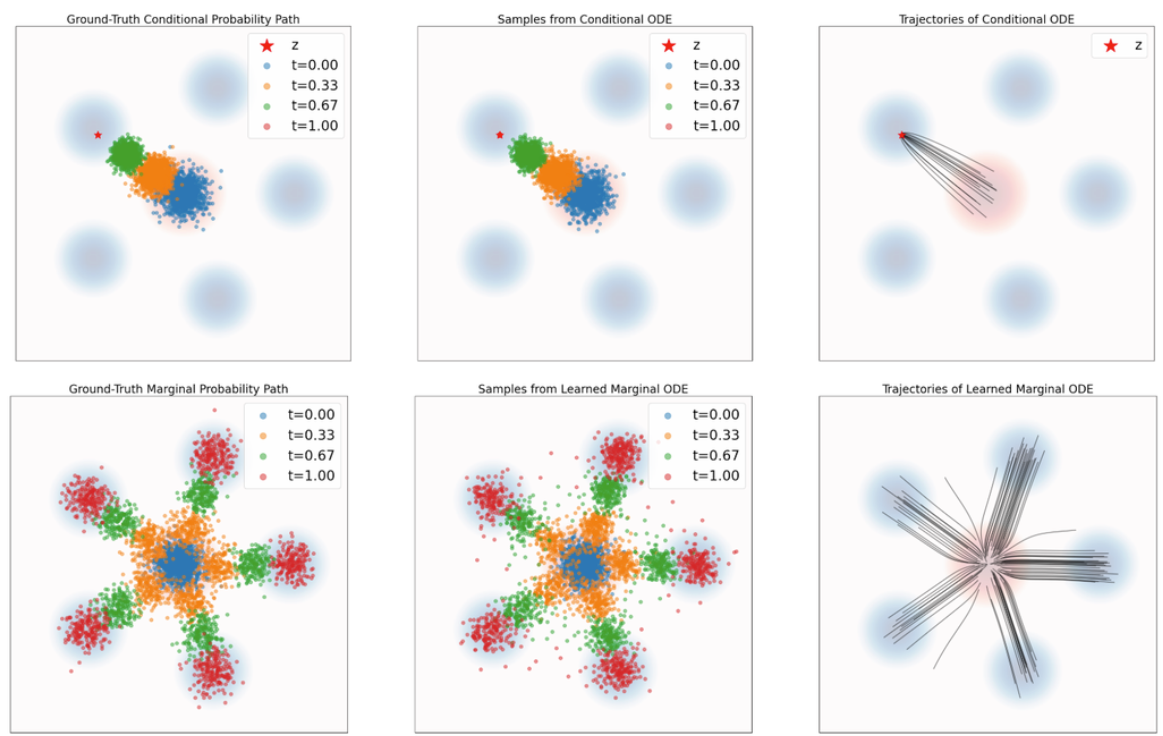
整个图中，浅蓝色背景是真实数据分布。浅红色背景是初始高斯分布
上面三个图是关于条件概率路径的图。

• 左边是条件概率路径的真实样本，也就是直接从精确的条件概率路径中采样得到。
• 中间是随时间变化的ODE样本，也就是模拟条件向量场，得到的一系列采样。
• 右边是模拟带有$u_t^{target}(x|z)$的DOE得到的轨迹，也就是对应的条件流函数。
  下面三个图是关于边缘概率路径的图。

3.3 条件和边缘得分函数

3.2我们为流模型构建了训练目标。这一节我们将这种推理推广到SDE。为此，我们先定义$p_t$的边缘得分函数(marginal socre funciton)为$\nabla \log p_t(x)$。然后就可以将前一节的ODE推广到这一节的SDE。

边缘得分函数表示"“在点 $x$上，概率密度上升最快的方向”。也就是高速我们，“从这里往哪个方向移动，样本会更像高概率区域（即更像真实数据）。”

定理13(SDE扩展技巧) 我们仍然可以像定理10那样，定义条件向量场和边缘向量场。其中条件向量场对应的ODE产生的条件概率路径。边缘向量场对应的ODE遵循边缘概率路径。然后，对于扩散系数${\sigma }_t\ge 0$，我们可以构造一个SDE，它遵循相同的边缘概率路径:
$$\begin{array}{rl}& X_0\sim p_{\text{init }},\mathrm{d}{X}_t=\left[u_t^{\mathrm{target}}\left(X_t\right)+\frac{{\sigma }_t^2}{2}\nabla \log p_t\left(X_t\right)\right]\mathrm{d}t+{\sigma }_t\mathrm{d}{W}_t\\ \Rightarrow & X_t\sim p_t(0\le t\le 1)\end{array}$$
如果把式子里面的边缘概率路径和边缘向量场替换成条件概率路径和条件向量场，恒等式也成立。

定理13的公式很有用。因为，与之前类似，我们可以通过条件得分函数$\nabla \log p_t(x\mid z)$来表达边缘得分函数:
$$\nabla \log p_t(x)=\frac{\nabla p_t(x)}{p_t(x)}=\frac{\nabla \int p_t(x\mid z)p_{\text{data }}(z)\mathrm{d}z}{p_t(x)}=\frac{\int \nabla p_t(x\mid z)p_{\text{data }}(z)\mathrm{d}z}{p_t(x)}=\int \nabla \log p_t(x\mid z)\frac{p_t(x\mid z)p_{\text{data }}(z)}{p_t(x)}\mathrm{d}z$$而条件得分函数使我们通常通过分析就可以知道的东西。可以参考下面的例子。

这里积分号里的右半部分和之前“通过条件向量场计算得到边缘向量场”的公式一样。

例14(高斯概率路径的得分函数)
对于高斯路径$p_t(x\mid z)=\mathcal{N}\left(x;{\alpha }_{t}z,{\beta }_t^2{I}_d\right)$，代入高斯概率密度公式:
$$\mathcal{N}\left(x;\mu ,{\sigma }^{2}I\right)={\left(2\pi {\sigma }^2\right)}^{-\frac{d}{2}}\exp \left(-\frac{\Vert x-\mu {\Vert }_2^2}{2{\sigma }^2}\right)$$我们可以计算得到条件得分函数为

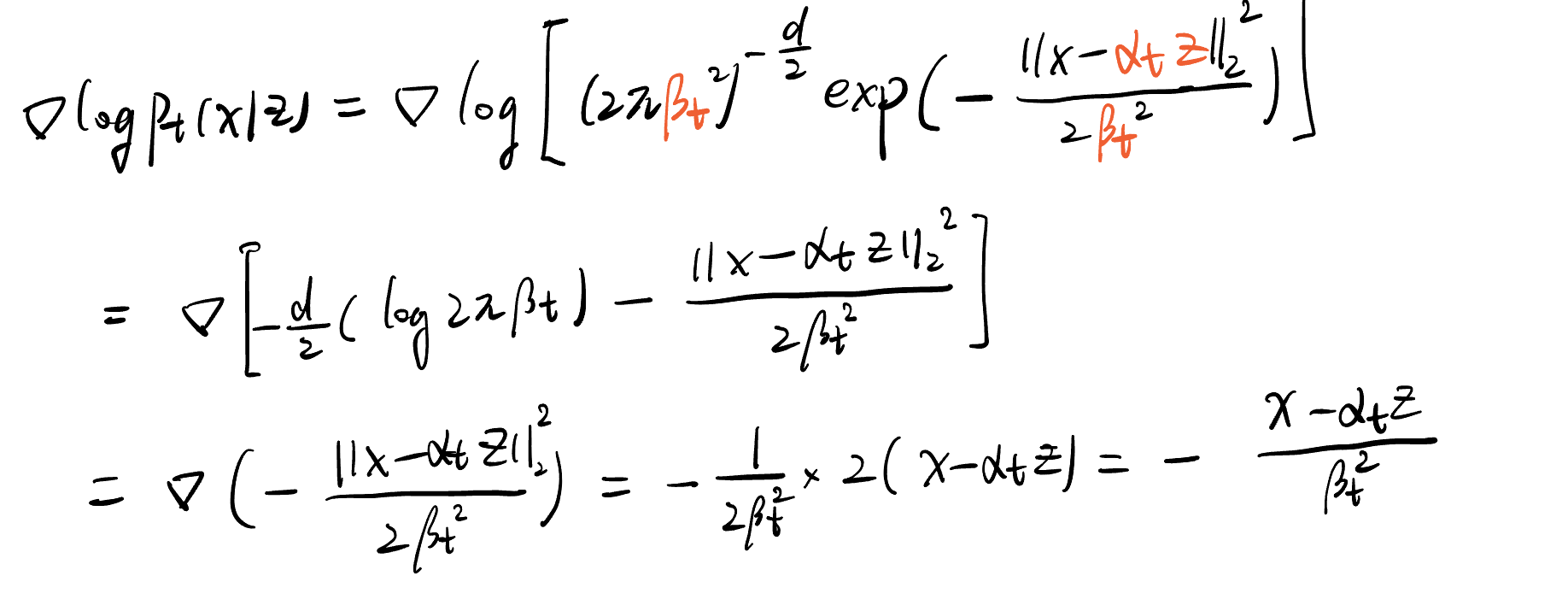
这里得分是$x$的线性函数。这是高斯分布的独特特征。

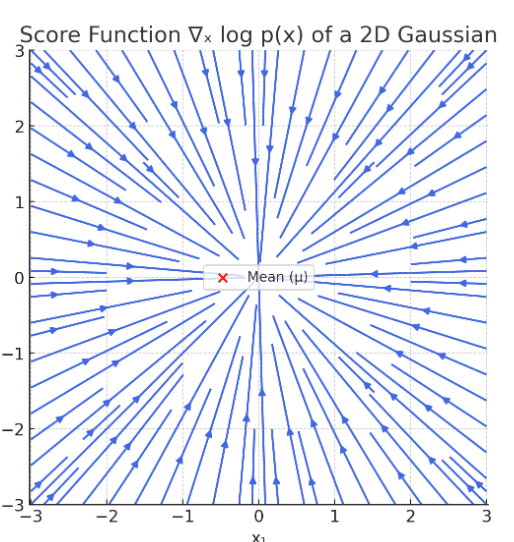
这是我让GPT画的高斯分布的得分函数:

本节的剩下部分，将通过福克-普朗克方程(Fokker-Plank方程)来证明定理13，该方程将连续性方程从ODE扩展到了SDE。为此，我们先定义Laplacian(拉普拉斯)算子$\Delta$:
$$\Delta w_t(x)=\sum _{i=1}^d\frac{{\partial }^2}{{\partial }^2{x}_i}{w}_t(x)=\mathrm{div}\left(\nabla w_t\right)(x)$$

梯度是将标量转化为向量场，散度是将向量场转化为标量。这里拉普拉斯算子是先把梯度算子作用在标量上得到向量场，然后再把散度算子作用在向量场上。
拉普拉斯算子本质上是空间二阶导数之和。把梯度算子的平方写成向量内积的话，也就是${\nabla }^2=\nabla \cdot \nabla$。那么拉普拉斯算子也可以记作${\nabla }^2$.

定理15(Fokker-Plank方程)：设$p_t$是一个概率路径，让我们考虑SDE
$$X_0\sim p_{\text{init }},\mathrm{d}{X}_t=u_t\left(X_t\right)\mathrm{d}t+{\sigma }_t\mathrm{d}{W}_t$$
则$X_t$对所有t都有分布$p_t$当且仅当对任何$x$和$t$，都有福克-普朗克方程成立:
$${\partial }_t{p}_t(x)=-\mathrm{div}\left(p_t{u}_t\right)(x)+\frac{{\sigma }_t^2}{2}\Delta p_t(x)$$详细证明见原文附录B。可以看到，如果扩散系数${\sigma }_t=0$，则福克-普朗克方程就是连续性方程。
附加的拉普拉斯项$\Delta p_t$可能很难理解。但它对应的就是扩散过程。

现在我们使用福克-普朗克方程来证明定理13。
定理13的证明。根据定理15，我们需要证明定理13中构造的SDE满足福克-普朗克方程。我们进行计算。

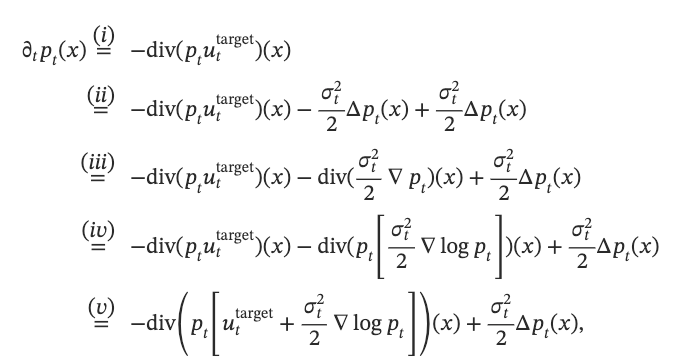
(i): 由于边缘向量场$u_t^{\text{target }}(x)$遵循边缘概率路径，所以满足连续性方程，（i)就使用了连续性方程。
(ii): 减去和增加了相同的项，即边缘概率路径作用拉普拉斯算子，然后乘以扩散系数平方，再除以2
(iii): 使用拉普拉斯算子的定义，展开成先求梯度，再求散度的形式
(iv): 使用了$\nabla \log p_t=\frac{\nabla p_t}{p_t}$
(v): 使用散度算子满足线性性质
所以定理13中定义的SDE满足$p_t$的福克-普朗克方程。根据定理15，这表明对应的$X_t$服从边缘概率路径。

备注16-郎之万(Langevin)动力学
当概率路径是静态的，即固定分布$p_t=p$时，上述构造有个特例。此时设置边际向量场为0向量，就会获得对应的SDE为:
$$\mathrm{d}{X}_t=\frac{{\sigma }_t^2}{2}\nabla \log p\left(X_t\right)\mathrm{d}t+{\sigma }_{t}d{W}_t$$这通常被称为Langevin动力学。
$p_t$ 是静态的事实意味着 ${\partial }_t{p}_t(x)=0$。
根据定理13，这些动力学满足静态路径$p_t=p$的福克-普朗克方程。因此，$p$是Langevin动力学的平稳分布，也就是有
$$X_0\sim p\Rightarrow X_t\sim p(t\ge 0)$$
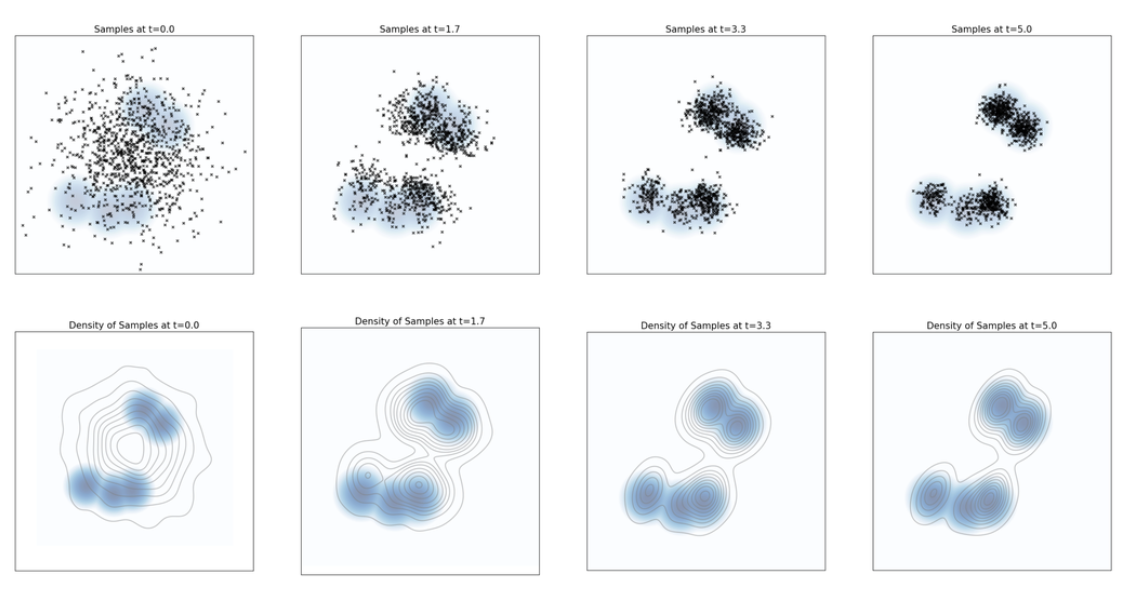
与许多马尔科夫链一样，这些动力学在相当一般的条件下收敛到平稳分布(如下图)。也就是说，即使初始分布不是分布p，在温和条件下，最后分布也会收敛到p分布。这一事实非常有用。因此它也作为例如 分子动力学 模拟以及贝叶斯统计学和自然科学中许多其他马尔可夫链蒙特卡罗 (MCMC) 方法的基础。
下图展示了例子在郎之万动力学下的演化。$p(x)$取为具有5个模态的高斯混合。其中模态是分布密度的局部最大点，也就是峰值。这里5个模态说明概率分布在空间中有5个高概率区域。上面是采样结果。下面是相同样本的核密度估计。可以看到，最终样本分布收敛到了平衡分布。

4 训练生成模型

本节描述如何训练神经网络来逼近训练目标。

4.1 流匹配

考虑$X_0\sim p_{\text{init }},\mathrm{d}{X}_t=u_t^{\theta }\left(X_t\right)\mathrm{d}t$给出的流模型。我们希望神经网络$u_t^{\theta }\left(X_t\right)$等于边缘向量场$u_t^{\text{target }}$。获得前者近似后者的直观方法是使用均方误差，即流匹配损失:
$$\begin{array}{rl}{\mathcal{L}}_{\mathrm{FM}}(\theta )& ={\mathbb{E}}_{t\sim \text{ Unif, }x\sim p_t}\left[{\Vert u_t^{\theta }(x)-u_t^{\text{target }}(x)\Vert }^2\right]\\ & \stackrel{(i)}{=}{\mathbb{E}}_{t\sim \text{ Unif, }z\sim p_{\text{data }},x\sim p_t(\cdot \mid z)}\left[{\Vert u_t^{\theta }(x)-u_t^{\text{target }}(x)\Vert }^2\right],\end{array}$$这个损失表示: 首先采样一个随机事件，然后从数据集中采样一个z，然后丛条件概率路径$p_t(\cdot |z)$中采样$x$，并通过神经网络计算$u_t^{\theta }(x)$。最后，计算神经网络的输出和边缘向量场$u_t^{\text{target }}(x)$的均方误差。
不过，虽然我们知道$u_t^{\text{target }}(x)$的公式:
$$u_t^{\text{target }}(x)=\int u_t^{\text{target }}(x\mid z)\frac{p_t(x\mid z)p_{\text{data }}(z)}{p_t(x)}\mathrm{d}z$$但是公式涉及积分，所以很难计算。而条件向量场$u_t^{\text{target }}(x\mid z)$则容易处理。于是我们考虑用神经网络近似条件向量场。为此，我们先定义条件流匹配损失:
$${\mathcal{L}}_{\mathrm{CFM}}(\theta )={\mathbb{E}}_{t\sim \text{ Unif, }z\sim p_{\text{data }},x\sim p_t(\cdot \mid z)}\left[{\Vert u_t^{\theta }(x)-u_t^{\text{target }}(x\mid z)\Vert }^2\right]$$这个损失可以被轻松计算。下面的定理表明，我们显式地计算可处理的条件向量场，等同于我们隐式地计算难以处理的边缘向量场。

定理18: 边缘流匹配损失等于条件流匹配损失，最多相差一个常数。
$${\mathcal{L}}_{FM}(\theta )={\mathcal{L}}_{CFM}(\theta )+C$$因此，它们梯度一致:
$${\nabla }_{\theta }{\mathcal{L}}_{FM}(\theta )={\nabla }_{\theta }{\mathcal{L}}_{CFM}(\theta )$$所以，在随机梯度下降最小化的情况下，两者等价。

证明略。
一旦神经网络训练完成。我们就可以通过模拟流模型来获得样本$X_1\sim p_{data}$。
下面的例子是高斯概率路径的

示例19(高斯条件概率路径的流匹配): 假设高斯概率路径$p_t(\cdot \mid z)=\mathcal{N}\left({\alpha }_{t}z;{\beta }_t^2{I}_d\right)$, 我们可以通过以下方式从条件路径中采样:
$$ϵ\sim \mathcal{N}\left(0,I_d\right)\Rightarrow x_t={\alpha }_{t}z+{\beta }_tϵ\sim \mathcal{N}\left({\alpha }_{t}z,{\beta }_t^2{I}_d\right)=p_t(\cdot \mid z)$$
之前已经推导过，对应的条件向量场由下面的式子给出:
$$u_t^{\text{target }}(x\mid z)=\left({\alpha }_t-\frac{{\dot{\beta }}_t}{{\beta }_t}{\alpha }_t\right)z+\frac{{\dot{\beta }}_t}{{\beta }_t}x$$
代入这个公式化后，赌赢的条件流匹配损失为:
$$\begin{array}{rl}{\mathcal{L}}_{CFM}(\theta )& ={\mathbb{E}}_{t\sim Unif,z\sim p_{\mathrm{data}},x\sim \mathcal{N}\left({\alpha }_{t}z,{\beta }_t^2{I}_d\right)}\left[{\Vert u_t^{\theta }(x)-\left({\alpha }_t-\frac{{\dot{\beta }}_t}{{\beta }_t}{\alpha }_t\right)z-\frac{{\dot{\beta }}_t}{{\beta }_t}x\Vert }^2\right]\\ & \stackrel{(i)}{=}{\mathbb{E}}_{t\sim Unif,z\sim p_{\mathrm{data}},ϵ\sim \mathcal{N}\left(0,I_d\right)}\left[{\Vert u_t^{\theta }\left({\alpha }_{t}z+{\beta }_tϵ\right)-\left({\alpha }_{t}z+{\beta }_tϵ\right)\Vert }^2\right]\end{array}$$
其中(i)中，把$x$替换为了${\alpha }_{t}z+{\beta }_tϵ$. 注意条件流匹配损失的简单性: 我们对数据点z采样，对噪声采样，然后取均方误差。
特别地，考虑更具体的${\alpha }_t=t$ 和 ${\beta }_t=1-t$ 的特殊情况，相应的条件概率路径为
$$p_t(x\mid z)=\mathcal{N}\left(tz,(1-t{)}^2\right)$$这被称为高斯CondOT概率路径。此时我们有${\dot{\alpha }}_t=1,{\dot{\beta }}_t=-1$, 于是条件流匹配损失为:
$${\mathcal{L}}_{cfm}(\theta )={\mathbb{E}}_{t\sim Unif,z\sim p_{\text{data }},ϵ\sim \mathcal{N}\left(0,I_d\right)}\left[{\Vert u_t^{\theta }(tz+(1-t)ϵ)-(z-ϵ)\Vert }^2\right]$$
许多先进模型都用这个程序训练，如Stable Diffusion 3，Meta 的 Movie Gen Video。

4.2 分数匹配

现在将ODE找到的算法扩展到SDEs。之前我们已经推导过，我们可以将目标ODE扩展到具有相同边缘分布的SDE，对应的SDE由以下方程给出:
$$\begin{array}{rl}\mathrm{d}{X}_t& =\left[u_t^{\mathrm{target}}\left(X_t\right)+\frac{{\sigma }_t^2}{2}\nabla \log p_t\left(X_t\right)\right]\mathrm{d}t+{\sigma }_t\mathrm{d}{W}_t\\ X_0& \sim p_{\text{init }}\\ \Rightarrow X_t& \sim p_t(0\le t\le 1)\end{array}$$
其中$u_t^{\text{target }}$是边缘向量场，$\nabla \log p_t(x)$是边缘得分函数，通过公式表示:
$$\nabla \log p_t(x)=\int \nabla \log p_t(x\mid z)\frac{p_t(x\mid z)p_{\text{data }}(z)}{p_t(x)}\mathrm{d}z$$
为了近似边缘得分函数，我们可以使用一个我们称之为得分网络$s_t^{\theta }:{\mathbb{R}}^d\times [0,1]\to {\mathbb{R}}^d$的神经网络。与之前一样，我们可以设计一个得分匹配损失和一个条件得分匹配损失:
$$\begin{array}{rl}{\mathcal{L}}_{\mathrm{SM}}(\theta )& ={\mathbb{E}}_{t\sim \mathrm{Unif},z\sim p_{\text{data }},x\sim p_t(\cdot \mid z)}\left[{\Vert s_t^{\theta }(x)-\nabla \log p_t(x)\Vert }^2\right]\text{ score matching loss }\\ {\mathcal{L}}_{\mathrm{CSM}}(\theta )& ={\mathbb{E}}_{t\sim \mathrm{Unif},z\sim p_{\text{data }},x\sim p_t\cdot \mid z)}\left[{\Vert s_t^{\theta }(x)-\nabla \log p_t(x\mid z)\Vert }^2\right]\text{ conditional score matching loss }\end{array}$$
和之前一样，最小化条件分数匹配损失是一个易于处理的替代方案，因为我们有以下定理:
定理20: 分数匹配损失和条件分数匹配损失之间只差一个常数。

证明略。

上述过程描述了训练扩散模型的vanilla过程。训练后，我们可以选择任意扩散系数${\sigma }_t\ge 0$，然后模拟 SDE:
$$X_0\sim p_{\text{init }},\mathrm{d}{X}_t=\left[u_t^{\theta }\left(X_t\right)+\frac{{\sigma }_t^2}{2}{s}_t^{\theta }\left(X_t\right)\right]\mathrm{d}t+{\sigma }_t\mathrm{d}{W}_t$$来生成样本$X_1\sim p_{\text{data }}$。理论上，每个${\sigma }_t$都应该在完美训练下生成样本$X_1\sim p_{data}$。但是实践中，我们会遇到两类错误:
(1)不能完美模拟SDE所产生的数值错误。
(2)训练错误，也就是模型$u_t^{\theta }$ 不完全等于 $u_t^{\text{target }}$。
因此，存在一个最佳的未知扩散系数-这可以通过仅仅测试我们不同的经验值来确定。

乍一看，如果我们现在想使用扩散模型而不是流模型，我们不得不学习$s_t^{\theta }$ 和 $u_t^{\theta }$似乎是一个劣势。然而，我们通常可以在一个具有两个输出的单个网络中直接同时学习$s_t^{\theta }$ 和 $u_t^{\theta }$，因此，额外的工作量是很小的。
此外，我们将看到，对于高斯概率路径的特殊情况，这两者可以互相转换，因此我们不必分别训练它们。

备注21(去噪扩散模型)

例22(去噪扩散模型: 高斯概率路径的评分匹配): 首先，让我们为高斯概率路径的情况实例化去噪得分匹配损失。之前我们已经推导过，对应的条件得分函数是$\nabla \log p_t(x\mid z)$ 的公式为:
$$\nabla \log p_t(x\mid z)=-\frac{x-{\alpha }_{t}z}{{\beta }_t^2}$$代入此公式后，条件得分匹配损失变为:
$$\begin{array}{rl}{\mathcal{L}}_{CSM}(\theta )& ={\mathbb{E}}_{t\sim U\text{ nif },z\sim p_{\text{data }},x\sim p_t(\cdot \mid z)}\left[{\Vert s_t^{\theta }(x)+\frac{x-{\alpha }_{t}z}{{\beta }_t^2}\Vert }^2\right]\\ & \stackrel{(i)}{=}{\mathbb{E}}_{t\sim U\text{ nif },z\sim p_{\text{data }},ϵ\sim \mathcal{N}\left(0,I_d\right)}\left[{\Vert s_t^{\theta }\left({\alpha }_{t}z+{\beta }_tϵ\right)+\frac{ϵ}{{\beta }_t}\Vert }^2\right]\\ & ={\mathbb{E}}_{t\sim U\text{ nif },z\sim p_{\text{data }},ϵ\sim \mathcal{N}\left(0,I_d\right)}\left[\frac{1}{{\beta }_t^2}{\Vert {\beta }_t{s}_t^{\theta }\left({\alpha }_{t}z+{\beta }_tϵ\right)+ϵ\Vert }^2\right]\end{array}$$
在(i)中，我们把$x$替换为${\alpha }_{t}z+{\beta }_tϵ$。可以看到，网络本质上是在预测用于损坏数据样本的噪声。因此，上述训练损失也被称为去噪得分匹配。人们很快意识到，上述损失对于接近0的${\beta }_t$来说，在数值上是不稳定的，即，去噪得分匹配仅仅在添加足够数量的噪声时才有效。因此，在一些早期工作中，建议在损失中删除常数$\frac{1}{{\beta }_t^2}$，并将网络参数化为噪声预测器网络${ϵ}_t^{\theta }:{\mathbb{R}}^d\times [0,1]\to {\mathbb{R}}^d$，通过令$-{\beta }_t{s}_t^{\theta }(x)={ϵ}_t^{\theta }(x)$。损失函数可以被表达为DDPM论文中的形式:
$${\mathcal{L}}_{DDPM}(\theta )={\mathbb{E}}_{t\sim Unif,z\sim p_{\text{data }},ϵ\sim \mathcal{N}\left(0,I_d\right)}\left[{\Vert {ϵ}_t^{\theta }\left({\alpha }_{t}z+{\beta }_tϵ\right)-ϵ\Vert }^2\right]$$
和之前一样，网络 ${ϵ}_t^{\theta }$ 本质上学习预测用于损坏数据样本 $z$ 的噪声。

在下面的算法中，我们总结了训练过程。
算法4(高斯概率路径的得分匹配训练过程):

除了它的简单性之外，高斯概率路径还有另一个有用的属性：通过学习 $s_t^{\theta }$ 或 ${ϵ}_t^{\theta }$ ，我们也自动学习 $u_t^{\theta }$ ，反之亦然：
命题1(高斯概率路径的转换公式):
对于高斯概率路径，条件（或 边际）向量场可以转换为条件（或 边际）得分：
$$\begin{array}{r}{u}_t^{\text{target }}(x\mid z)=\left({\beta }_t^2\frac{{\alpha }_t}{{\alpha }_t}-{\dot{\beta }}_t{\beta }_t\right)\nabla \log p_t(x\mid z)+\frac{{\alpha }_t}{{\alpha }_t}x\\ u_t^{\text{target }}(x)=\left({\beta }_t^2\frac{{\dot{\alpha }}_t}{{\alpha }_t}-{\dot{\beta }}_t{\beta }_t\right)\nabla \log p_t(x)+\frac{{\dot{\alpha }}_t}{{\alpha }_t}x\end{array}$$
上述边际向量场的公式在文献中被称为 概率流 ODE（更确切地说，是相应的 ODE）。
证明略。

这个命题高速我们，可以使用转换公式将得分网络和向量场网络相互参数化，通过
$$u_t^{\theta }=\left({\beta }_t^2\frac{{\alpha }_t}{{\alpha }_t}-{\dot{\beta }}_t{\beta }_t\right)s_t^{\theta }(x)+\frac{{\alpha }_t}{{\alpha }_t}x$$我们可以用得分网络表示向量场网络。
。类似的，只要${\beta }_t^2{\alpha }_t-{\alpha }_t{\beta }_t{\beta }_t\ne 0$（对于 $t\in [0,1)$ 始终为真），就可以得出$$s_t^{\theta }(x)=\frac{{\alpha }_t{u}_t^{\theta }(x)-{\dot{\alpha }}_{t}x}{{\beta }_t^2{\alpha }_t-{\alpha }_t{\beta }_t{\beta }_t}$$我们可以通过用向量场网络表示得分网络。
使用这些参数化，对于高斯概率路径的场合，我们可以证明去噪得分匹配损失和条件流匹配损失只差一个常数。因此，对于高斯概率路径，无需单独训练边缘得分和边缘向量场，只需要知道其中一个就足以计算另一个。特别是，我们可以选择是使用流匹配还是得分匹配来训练它。

4.3 扩散模型文献指南(略)

5.构建图像生成器

前面我们学习了如何训练一个流匹配或扩散模型，从一个分布 $p_{\text{data }}(x)$ 中采样。这个方法是通用的，可以应用于不同的数据类型和应用。本节，我们将学习如何应用这个框架构建图像或视频生成器。为了构建这样的模型，我们缺少两个主要组成成分:
(1)条件生成(引导)。例如, 我们如何生成符合特定文本提示的图像，以及我们现有的目标如何适当地适应这个目的。我们将了解classifier-free guidance。这是一种用于提高条件生成质量的常用技术。
(2)讨论常见的神经网络架构，再次侧重为图像和视频设计的架构。
最后，我们将深入研究上面提到的两种最先进的图像和视频模型——Stable Diffusion 和 Meta MovieGen——让你了解大规模操作的方式。

暂略。