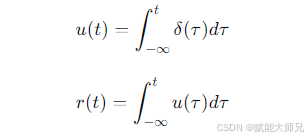一阶时域信号的分类

信号与系统分析中最核心的三个基本一阶时域信号：单位阶跃信号、单位斜变信号和单位冲击信号。理解它们是理解整个系统分析的基础。

一、单位阶跃信号

单位阶跃信号通常用符号 u(t) 或 ε(t) 表示。

定义

在 t=0 时刻，信号从0跃变到1。其值在跳变点可以定义为1、0或1/2，但在经典信号分析中通常定义为1。

物理意义与作用

“开关”作用：它可以用来表示一个在 t=0 时刻突然接通（或开始作用）的直流信号。

• 例如，一个1V的直流电源在 t=0 时接通，其电压可表示为：v(t)=1⋅u(t) V。

表示信号的作用区间：利用单位阶跃信号，可以方便地表示任何有始信号或截取信号的某一段。

• 例如，一个门函数（矩形脉冲）可以表示为两个阶跃信号之差：

  G(t)=u(t−a)−u(t−b)

  这表示一个从 t=a 开始，到 t=b 结束的矩形脉冲。

因果系统的表征：因果系统的单位冲激响应 h(t) 必须满足 h(t)=0,∀t<0，这通常可以写成 h(t)=[某些表达式]⋅u(t)。

二、单位斜变信号

单位斜变信号通常用符号 r(t) 表示。

定义

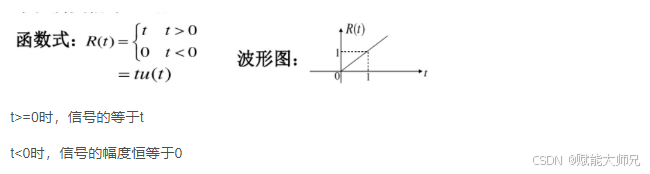
它也可以简洁地写成：r(t)=t⋅u(t)。

物理意义与作用

表示线性增长：它可以用来模拟一个从t=0 时刻开始随时间线性增长的物理量，例如匀速运动物体的位移。

与其他信号的关系：

• 与阶跃信号的关系：单位斜变信号是单位阶跃信号的积分。

  

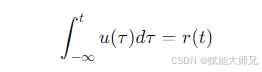
  直观理解：阶跃信号在 t<0 时为零，积分为0；在 t>0 时，对常数1进行积分，结果就是 t。

• 与冲击信号的关系：单位阶跃信号是单位斜变信号的导数（在广义函数意义上）。我们接下来会看到冲击信号。

三、单位冲击信号

单位冲击信号，也称为狄拉克δ函数，用符号 δ(t) 表示。

注意：它不是一个普通的函数，而是一个“广义函数”或“分布”。它通过其对其他函数的作用来定义。

定义（通过性质定义）

1. 强度（面积）为1：

   

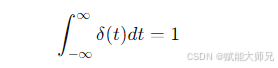
2. 抽样（筛选）特性：这是其最核心、最常用的性质。对于任意在 t=0 处连续的函数 f(t)，

   

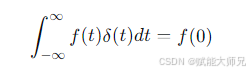
   更一般地，对于时移的冲击δ(t−T)，

   

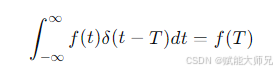
   这就像一把“筛子”，能从f(t) 中筛选出在t=T 时刻的值。

直观理解

我们可以将δ(t) 看作是一个宽度极窄、幅度极高、但总面积（强度）始终保持为1的矩形脉冲的极限情况。

当脉冲宽度 ϵ→0 时，脉冲高度1/ϵ→∞，但其面积始终为 (1/ϵ)×ϵ=1。

物理意义与作用

理想化的瞬时现象：

• 力学中，一个作用时间极短、冲量为1的力。

• 电路中，一个持续时间极短、电荷量为1的电流脉冲。

系统的“指纹”：在LTI（线性时不变）系统分析中，单位冲激响应 h(t) 是系统在单位冲击信号 δ(t) 激励下的零状态响应。知道了 h(t)，就可以通过卷积求出系统对任意输入信号的响应。这是时域分析法的基石。

建模突变量：可以用来表示信号中的跳变或不连续点。

四、一阶时域信号总结

这三个基本信号通过微分和积分运算紧密相连，构成了一个完美的关系链。

从下往上，是微分关系：

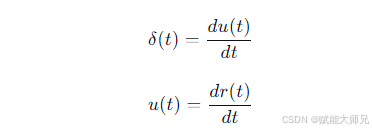
从上往下，是积分关系：