【C++】分治-归并排序算法习题

🎆个人主页：夜晚中的人海

今日语录：人一生的价值，不应该用时间去衡量，而是用深度去衡量。

🏠一、排序数组

题目链接：排序数组

题目描述：

解题思路：
1.首先将数组划分成两部分，采取中间值划分的策略

2.其次将左右区间分别进行排序

3.创建一个辅助数组用来合并两个有序数组

4.最后将其还原成原数组

代码实现：

class Solution {//辅助数组vector<int> tmp;
public:vector<int> sortArray(vector<int>& nums) {tmp.resize(nums.size());merge(nums,0,nums.size() - 1);return nums;}void merge(vector<int>& nums,int left,int right){if(left >= right)return;int mid = (left + right) >> 1;//[left,mid][mid + 1,right]merge(nums,left,mid);merge(nums,mid + 1,right);int cur1 = left,cur2 = mid + 1,i = 0;//合并两个有序数组while(cur1 <= mid && cur2 <= right){tmp[i++] = nums[cur1] > nums[cur2] ? nums[cur2++] : nums[cur1++];}while(cur1 <= mid)tmp[i++] = nums[cur1++];while(cur2 <= right)tmp[i++] = nums[cur2++];//还原for(int i = left;i <= right;i++){nums[i] = tmp[i - left];}}
};

🚀二、数组中的逆序对

题目链接：数组中的逆序对

题目描述：

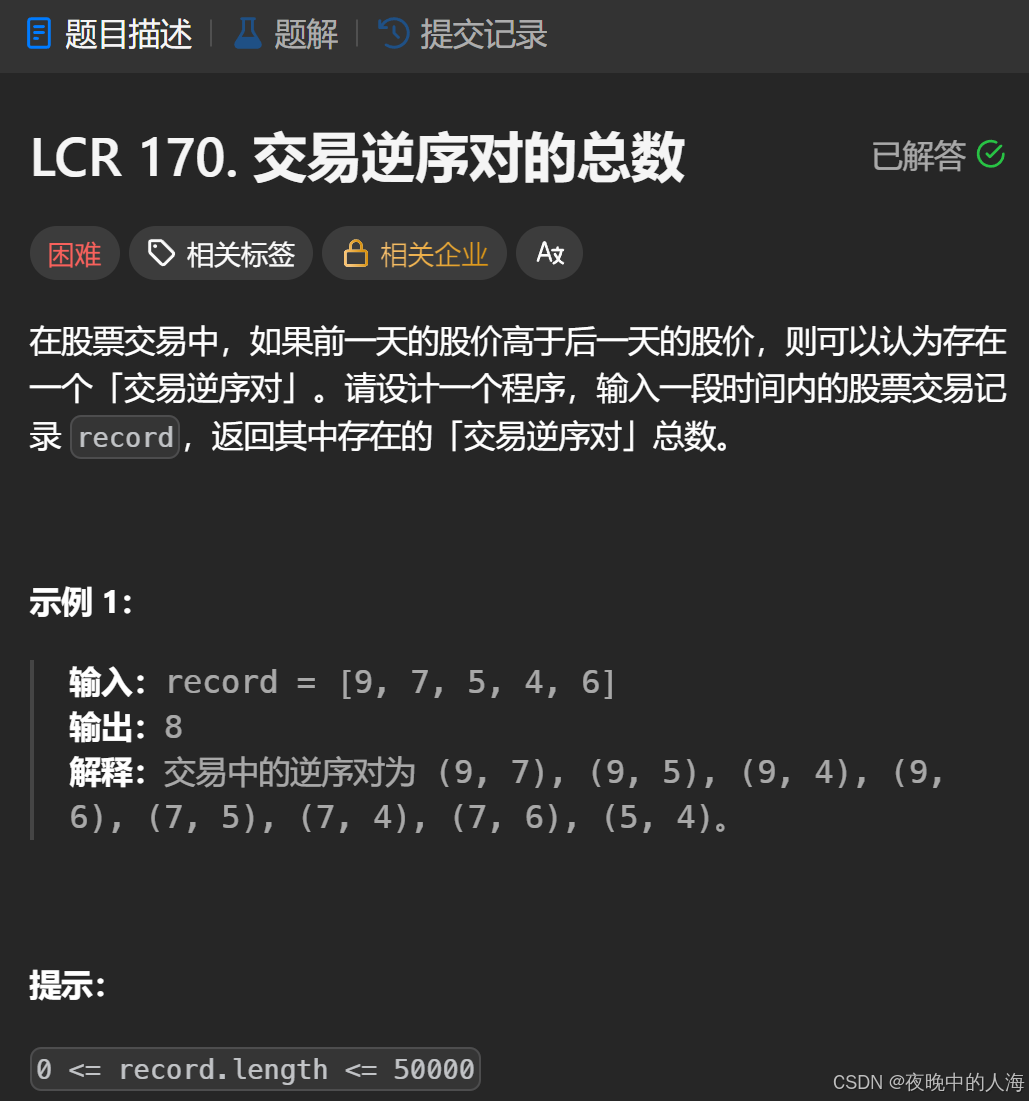
解题思路：
1.首先将数组从中间划分成两部分，因此我们有三种选择逆序对的方案：[逆序对中的元素全部从左数组中选取][逆序对的元素全部从右数组中选取][逆序对中的元素一个在左数组，另一个在右数组]将上述选取方案累加起来就是总的逆序对的个数

2.而上述选取的方案正好对应归并排序的排序过程，根据归并排序的特性，我们就可以很快统计出逆序对的数量，从而解决问题

代码实现：

使用升序和降序都可以进行解决

升序版本：

class Solution {vector<int> tmp;
public:int reversePairs(vector<int>& record) {tmp.resize(record.size());return merge(record,0,record.size() - 1);}int merge(vector<int>& record,int left,int right){int ret = 0;if(left >= right)return 0;int mid = (left + right) >> 1;//左边的个数 + 排序ret += merge(record,left,mid);//右边的个数 + 排序ret += merge(record,mid + 1,right);//一左一右的个数int cur1 = left,cur2 = mid + 1,i = 0;while(cur1 <= mid && cur2 <= right){//升序if(record[cur1] <= record[cur2]){tmp[i++] = record[cur1++];}else{ret += mid - cur1 + 1;tmp[i++] = record[cur2++];}}while(cur1 <= mid)tmp[i++] = record[cur1++];while(cur2 <= right)tmp[i++] = record[cur2++];//还原for(int i = left;i <= right;i++){record[i] = tmp[i - left];}return ret;}
};

降序版本：

class Solution {vector<int> tmp;
public:int reversePairs(vector<int>& record) {tmp.resize(record.size());return merge(record,0,record.size() - 1);}int merge(vector<int>& record,int left,int right){int ret = 0;if(left >= right)return 0;int mid = (left + right) >> 1;//左边的个数 + 排序ret += merge(record,left,mid);//右边的个数 + 排序ret += merge(record,mid + 1,right);//一左一右的个数int cur1 = left,cur2 = mid + 1,i = 0;while(cur1 <= mid && cur2 <= right){//降序（升降核心代码）if(record[cur1] <= record[cur2]){tmp[i++] = record[cur2++];}else{ret += right - cur2 + 1;tmp[i++] = record[cur1++];}}while(cur1 <= mid)tmp[i++] = record[cur1++];while(cur2 <= right)tmp[i++] = record[cur2++];//还原for(int i = left;i <= right;i++){record[i] = tmp[i - left];}return ret;}
};

🏖️三、计算右侧小于当前元素的个数

题目链接：计算右侧小于当前元素的个数

题目描述：

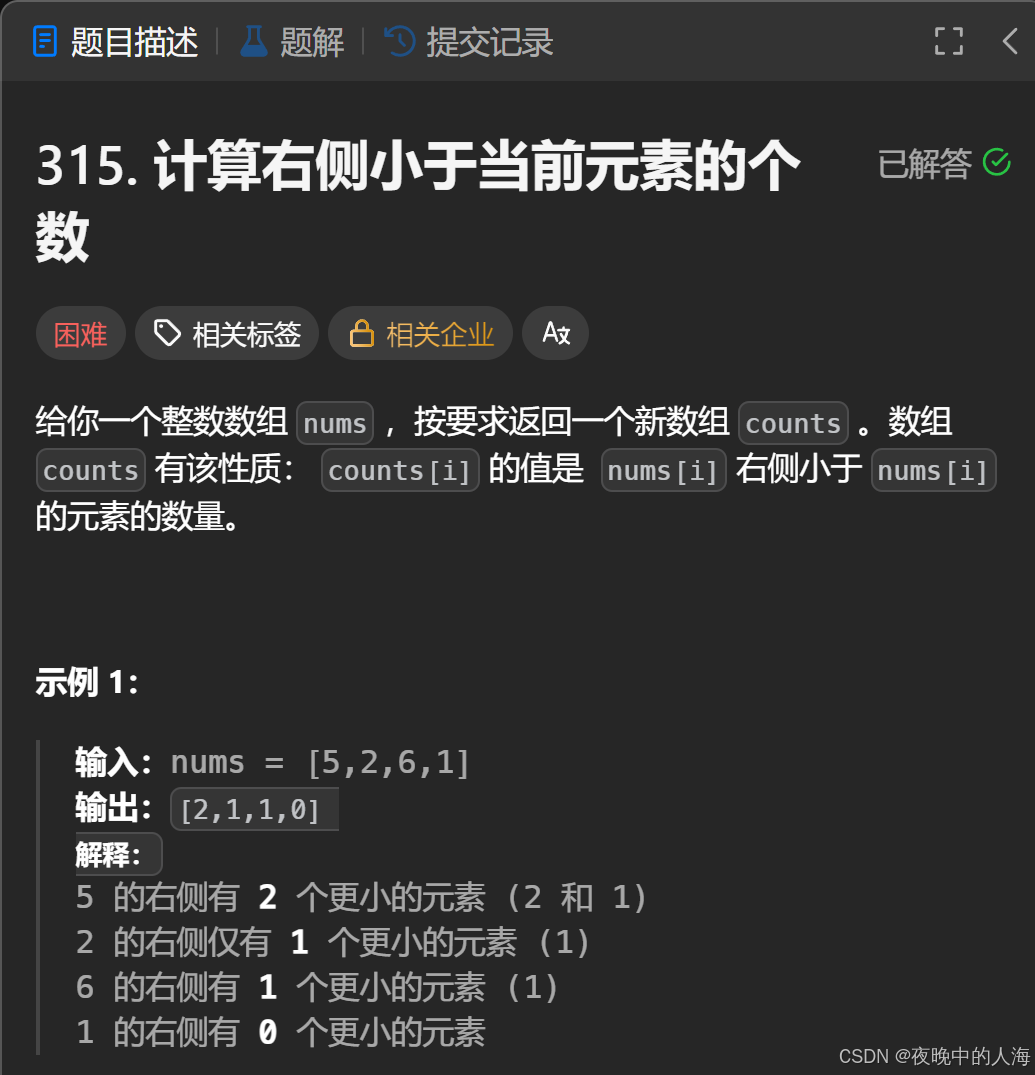
解题思路：
1.我们一共需要创建四个辅助数组：index（用于记录记录数组下标）ret（用于记录结果）tmpnums（用于排序的辅助数组）indexnums（用于记录排序的数组下标）

2.将数组划分成两部分，分别对左右区间的数组进行排序

3.合并两个有序区间，统计出逆序对的数量（注意：不仅要将数据放在对应的位置上，还要将数组对应的下标放在对应的位置上，因此两者是绑定移动的）

4.最后还原数组，得出结果

代码实现：

class Solution {//初始化数组下标vector<int> index;//结果数组vector<int> ret;//排序的辅助数组int tmpnums[100000];//处理下标的辅助数组int indexnums[100000];
public:vector<int> countSmaller(vector<int>& nums) {ret.resize(nums.size());index.resize(nums.size());for(int i = 0;i < nums.size();i++){//初始化index数组index[i] = i;}merge(nums,0,nums.size() - 1);return ret;}void merge(vector<int>& nums,int left,int right){if(left >= right)return;int mid = (left + right) >> 1;merge(nums,left,mid);merge(nums,mid + 1,right);int cur1 = left,cur2 = mid + 1,i = 0;while(cur1 <= mid && cur2 <= right){//降序版本if(nums[cur1] <= nums[cur2]){tmpnums[i] = nums[cur2];indexnums[i++] = index[cur2++];}else{ret[index[cur1]] += right - cur2 + 1;tmpnums[i] = nums[cur1];indexnums[i++] = index[cur1++];}}while(cur1 <= mid){tmpnums[i] = nums[cur1];indexnums[i++] = index[cur1++];}while(cur2 <= right){tmpnums[i] = nums[cur2];indexnums[i++] = index[cur2++];}//还原for(int i = left;i <= right;i++){nums[i] = tmpnums[i - left];index[i] = indexnums[i - left];}}
};

⭐四、翻转对

题目链接：翻转对

题目描述：

解题思路：
1.跟逆序对的解题思路类似，可以将翻转对划分成三个区间：左区间的翻转对数量，右区间的翻转对数量，一左一右选择时的翻转对数量，将三种划分结果累加起来得到总的翻转对数量

2.由题可知，我们统计的是左区间的元素大于右区间元素的两倍时才统计，因此在归并排序之前先统计翻转对的数量，减少时间成本

代码实现：

class Solution {vector<int> tmp;
public:int reversePairs(vector<int>& nums) {int n = nums.size();tmp.resize(n);return merge(nums,0,n - 1);}int merge(vector<int>& nums,int left,int right){if(left >= right)return 0;int ret = 0;int mid = (left + right) >> 1;ret += merge(nums,left,mid);ret += merge(nums,mid + 1,right);int cur1 = left,cur2 = mid + 1,i = 0;//统计翻转对的数量while(cur1 <= mid){//降序while(cur2 <= right && nums[cur2] >= nums[cur1] / 2.0){cur2++;if(cur2 > right)break;}ret += right - cur2 + 1;cur1++;}//合并两个有序数组cur1 = left,cur2 = mid + 1;while(cur1 <= mid && cur2 <= right){tmp[i++] = nums[cur1] <= nums[cur2] ? nums[cur2++] : nums[cur1++];}while(cur1 <= mid){tmp[i++] = nums[cur1++];}while(cur2 <= right){tmp[i++] = nums[cur2++];}//还原for(int i = left;i <= right;i++){nums[i] = tmp[i - left];}return ret;}
};