简析单目相机模型中的针孔模型
目录
1. 前言
2.针孔模型中的四大坐标系
3.笛卡尔坐标和齐次坐标
4.针孔模型内参矩阵的几何推导流程
前言
单目相机模型的核心思想是描述现实三维世界中的一个点是如何被投影到二维图像平面上的点,而单目相机模型分为针孔模型和畸变模型,针孔相机模型是用于描述理想的透视投影几何关系,但是由于实际的相机镜头并非理想的针孔,因为透镜的物理形状和装配的误差会引起图像的扭曲发生畸变,所以有了畸变模型,该模型描述实际相机镜头因物理缺陷导致的图像扭曲。本篇博客将对单目模型中的针孔模型进行解析,分析其原理和公式推导得到内参矩阵。
针孔模型中的四大坐标系
在针孔模型中定义了以下四个坐标系:
1.像素坐标系:该坐标系是最终得到的图像中的坐标系,其原点位于图像的左上角,单位为像素(图1中的紫色坐标系)
2.图像坐标系:该坐标系是成像平面中的坐标系,其原点位于成像平面与光轴的交点,该点也被称为主点(图1中的绿色坐标系,其中红色的线段可表示光轴)
3.相机坐标系:该坐标系以相机的光心为原点,以相机的视角来观察世界的坐标系(图1中的蓝色坐标系)
4.世界坐标系:该坐标系用于描述三维现实空间的基准坐标系,用来定义所有物体在现实空间中的绝对位置(图1中的黑色坐标系)
PS:对于各个坐标系可以参考图1,能结合相机模型更好的理解四个坐标系的不同
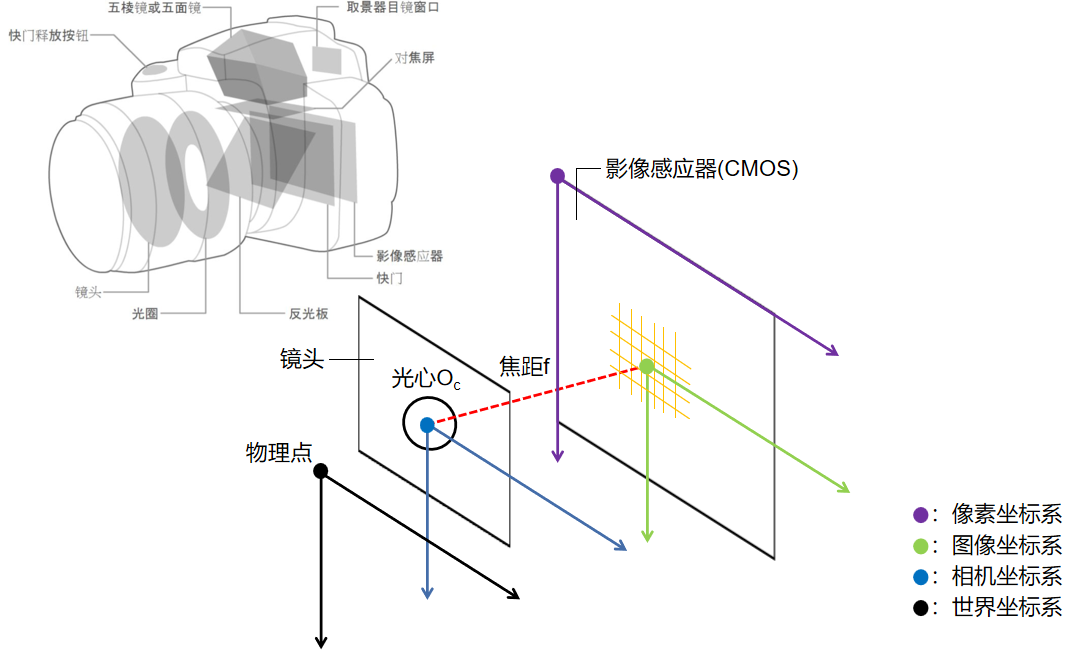
图1.四大坐标系
笛卡尔坐标和齐次坐标
笛卡尔坐标是我们当前理解的坐标系,就是使用N个数值来表示N维空间中的一个点。例如在2维平面上的点可以使用(X,Y)来表示,3维空间中的点可以使用(X,Y,Z)来表示。而齐次坐标是笛卡尔坐标的扩展表示方法,它使用了N+1个数值来表示N维空间中的一个点,例如在2维平面上的点可以使用(X,Y,W)来表示,3维空间中的点可以使用(X,Y,Z,W)来表示,这多出来的W参数实际上就是齐次坐标的尺度因子。
为什么笛卡尔坐标已经能清晰的表示N维空间的物体,还要引入迪卡尔坐标?这是因为在笛卡尔坐标下,点和向量在表示上没有区别都是(X,Y,Z),这在进行几何变换时会造成混淆。而在齐次坐标下点的W分量不为零,通常表示为(X,Y,Z,1),而向量的W分量为零表示为(X,W,Y,Z,0)。并且笛卡尔坐标中的平移是使用向量加法表示,旋转是使用矩阵乘法表示,而齐次坐标则可以把平移和旋转都使用矩阵乘法表示。
对于齐次坐标和迪卡尔坐标的转换则可以参考下图:

图2.齐次坐标和迪卡尔坐标的转换
PS:在齐次坐标中,如果比例因子W为零,那么这个点就是一个无穷远的点或者方向向量
针孔模型内参矩阵的几何推导流程
本小节主要是推理了如何获取内参矩阵,为了更好的理解推导流程和坐标系之间的关系,我们通过对图1中的图像进行抽离和标注得到了图3。在图3中世界坐标系可以记为O-XYZ,相机坐标系可以记为-
,图像坐标系可以记为
-X'Y',具体参考下图。而图中的物理点P(X,Y)是以世界坐标系为坐标来计算的,映射到成像平面的点P'(X',Y')则是以图像坐标系进行计算的。
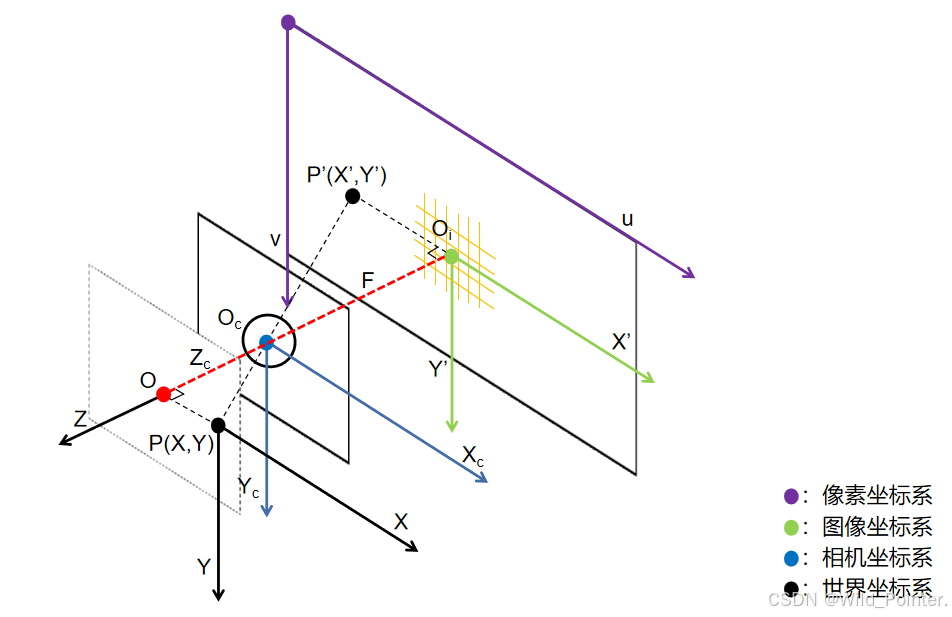
图3.点与坐标系的关系
通过调整图3的观察视角,我们可以发现俯视时物理点P,光轴,点O,点,点
和点P'(X',Y')可以构成一个相似三角形,具体如图4。
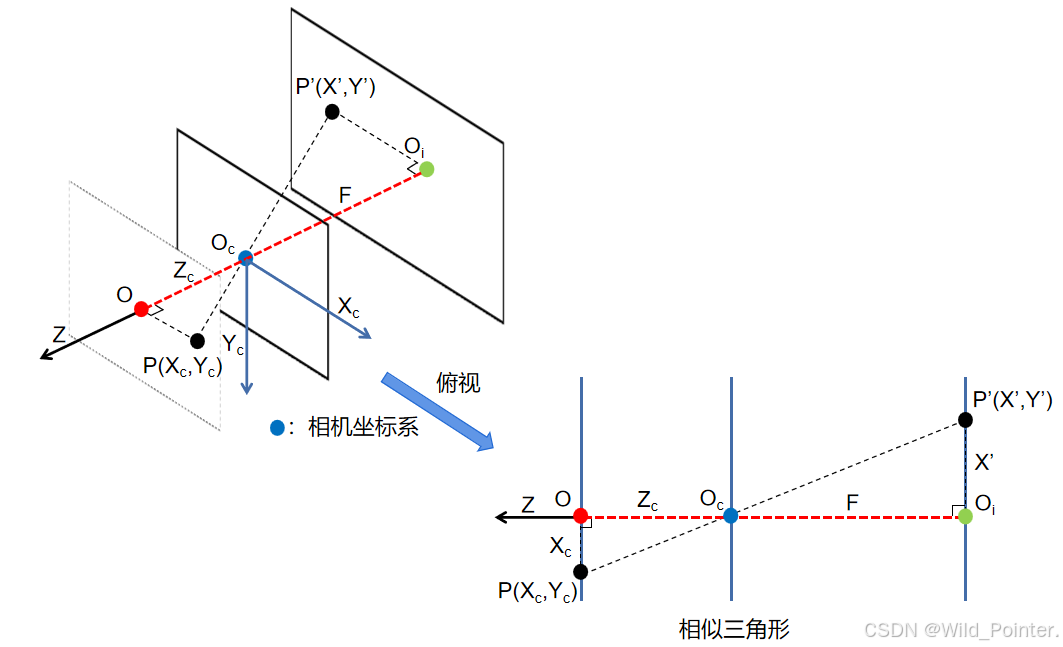
图4.俯视点和各个成像平面
为了计算物理点P(,
)映射到成像平面上的点的坐标,我们知道相似三角形各个相对应的边是成比例的,这是相似三角形的特性。对此我们可以得出以下等式(此处的物理点是以相机为视角进行观察,坐标由原来的世界坐标系(X,Y)变为相机坐标系(
,
)):
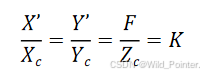
通过等式,我们可以得出成像平面是点的X'和Y'坐标的计算公式如下:
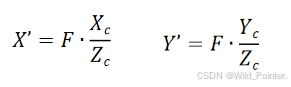
此时计算的坐标点是以笛卡尔坐标进行运算的,为了方便后续的运算我们将其转换为齐次坐标,并且引入比例因子W(第二小节讲解过笛卡尔坐标和齐次坐标的相互转换)。并且由于上述计算X'和Y'的公式包含除法是非线性的,对此我们将所在等式的位置调整,由除法运算变换为乘法运算,将非线性处理调整为线性处理得到一下计算映射到成像平面上点的坐标计算公式(其中F为焦距,
为深度值即光轴到关心的距离):
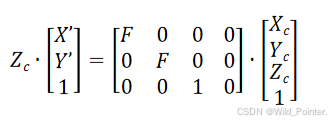
我们知道了要如何计算在成像平面上点的坐标,现在我们将视角调整到成像平面上,如下图:
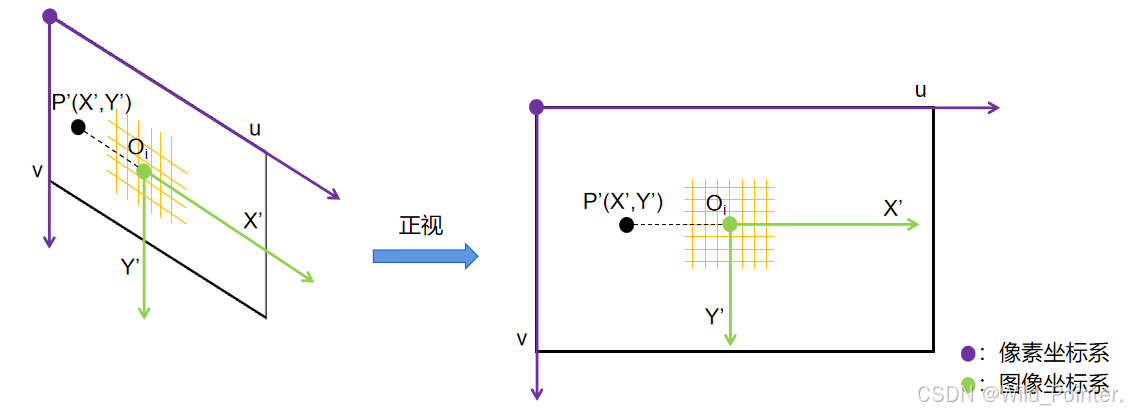
图5.成像平面正式图
图5中映射点P'的坐标为(X',Y'),这是以图像坐标系为基准观察的,如果我们将观察的基准调整为像素坐标系的话则映射点P'的坐标应该为(u,v),那么我们应该如何计算实际的u和v呢?我们知道成像平面是影响感应器(CMOS),而CMOS是由多个有源像素传感器组成,为了计算u和v的值我们就需要每一个有源像素传感器的物理宽度和高度,具体的CMOS原理图如下:
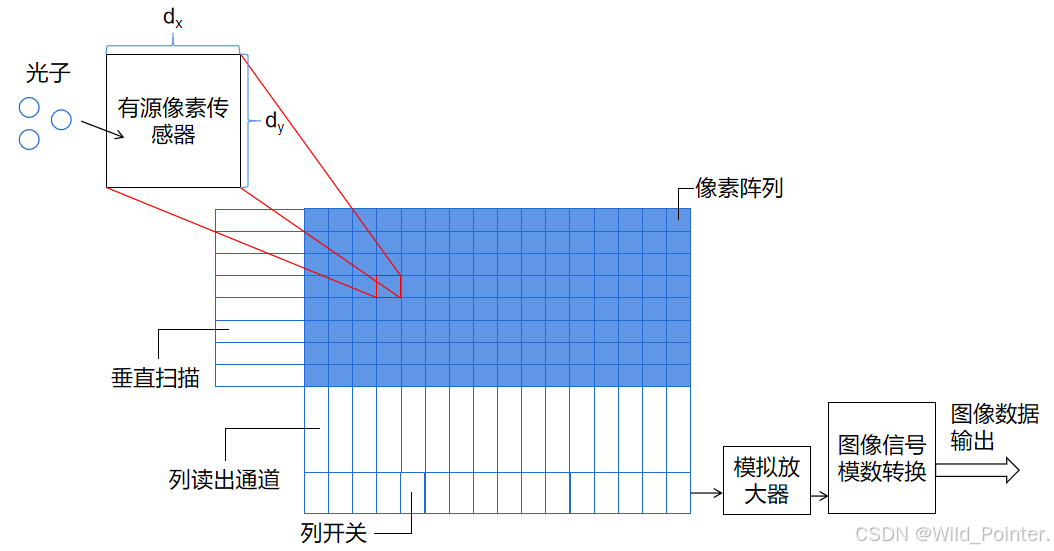
图6.CMOS原理图
现在我们把每一个有源像素传感器的物理宽度和高度使用和
来表示,对此我们需要把图像坐标系中的X'和Y'转换为u和v表示,为此我们需要知道点
在像素坐标系中的位置(
和
)。假设当前的成像平面的大小为640*640,那么点
在像素坐标系中的位置应该是320*320,具体公式如下:
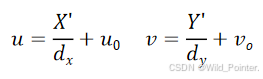
为了方便理解上述公式中的和
,我们可以假设X'的坐标是0.012毫米,而CMOS中的一个有源像素传感器的宽度是0.006毫米,那么
的结果为2。则表示该点在水平方向上距离点
有两个像素的物理距离,即
可以代表物理距离相当于多少个像素的宽度。对于上述公式其实还是以笛卡尔坐标进行运算的,为了转换为矩阵运算我们需要将笛卡尔坐标转换为齐次坐标,具体的转换过程和结果如下:
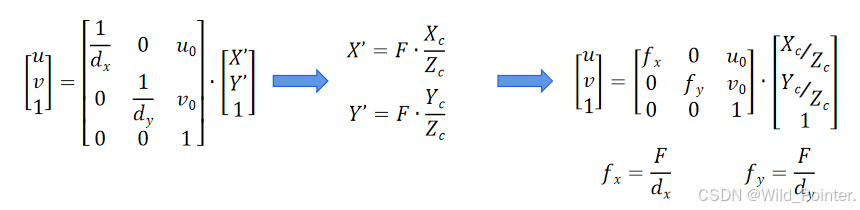
为了更直观的理解最终的结果,我们也可以写成以下形式:
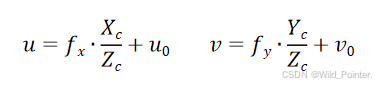
而我们得到的结果中,相机的内参矩阵K为:
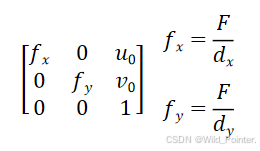
得到了内参矩阵,我们就可以从图像中测量距离,估计物体的姿态并重建三维场景。并且通过针孔模型得到的内参矩阵,能为畸变模型提供标尺,使得畸变的修正在正确的几何坐标下进行。
