当前位置：首页 > news >正文

计算机图形学·12 OpenGL Transformations

news 2025/11/9 14:45:47

本文是记录专业课“计算机图形学”的部分笔记，参考教材为Angel的第八版交互式计算机图形学——基于WebGL 2.0的自顶向下方法。

1、在OpenGL中，矩阵是状态的一部分，有以下几类：①GL_MODELVIEW 模型视图；②GL_PROJECTION 投影；③GL_TEXTURE 纹理；④GL_COLOR 颜色。而当前变换矩阵(CTM)就是一个4x4阶的齐次坐标矩阵，它作为状态的一部分，被应用到经过流水线中的所有顶点。CTM是在应用程序中定义的，并被加载到变换单元中。CTM可以被改变，改变的方法是上载一个新的CTM或者右乘一个矩阵：
Load an identity matrix: C <- I
Load an arbitrary（任意的） matrix: C <- M
Load a translation matrix: C <- T
Load a rotation matrix: C <- R
Load a scaling matrix: C <- S
Postmultiply by an arbitrary matrix: C <- CM
Postmultiply by a translation matrix: C <- CT
Postmultiply by a rotation matrix: C <- CR
Postmultiply by a scaling matrix: C <- CS

2、现在来看具体函数。glLoadIdentity()是加载单位阵，相当于重置矩阵。也可以右乘①glRotatef(theta, vx, vy, vz) 其中theta为角度，(vx, vy, vz)定义旋转轴，默认转向为逆时针；②glTranslatef(dx, dy, dz) 平移变换；③glScalef( sx, sy, sz) 比例变换，原点为不动点。每个函数可以是f还可以是d(double)类型。

一个例子，固定点为(1.0, 2.0, 3.0)，绕z轴旋转30°：

 glMatrixMode(GL_MODELVIEW);glLoadIdentity();//从这开始，记住在程序中最后指定的矩阵是最先被执行的操作glTranslatef(1.0, 2.0, 3.0);glRotatef(30.0, 0.0, 0.0, 1.0);glTranslatef(-1.0, -2.0, -3.0);

可以这么理解：

3、glLoadMatrixf(m) 可以上载应用程序中定义的矩阵、使之替换当前CTM；glMultMatrixf(m) 可以让m乘在已有矩阵的右边。而许多时候，需要保存变换矩阵，待稍后再用。这可以通过遍历层次数据结构、当执行显示列表时避免状态改变来实现，OpenGL则为每种类型的矩阵维持栈结构：
glPushMatrix() //压入，保存
glPopMatrix() //弹出，恢复

4、此外，状态中有些信息是以矩阵形式保存的，可以利用查询函数读入矩阵（以及其它部分的状态），比如glGetIntegerv、glGetFloatv、glGetBooleanv、glGetDoublev、glIsEnabled：```
double m[16];
glGetFloatv(GL_MODELVIEW, m);
5、变换的应用：旋转立方体（应用空闲函数旋转立方体，鼠标函数改变旋转的方向）。部分代码示例：

void main(int argc, char **argv) 
{ glutInit(&argc, argv);glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB |GLUT_DEPTH);glutInitWindowSize(500, 500);glutCreateWindow("colorcube");glutReshapeFunc(myReshape);glutDisplayFunc(display);glutIdleFunc(spinCube);glutMouseFunc(mouse);glEnable(GL_DEPTH_TEST);glutMainLoop();
}void spinCube() 
{
theta[axis] += 2.0;
if( theta[axis] > 360.0 ) theta[axis] -= 360.0;
glutPostRedisplay();
}void mouse(int btn, int state, int x, int y)
{if(btn==GLUT_LEFT_BUTTON && state == GLUT_DOWN) axis = 0;if(btn==GLUT_MIDDLE_BUTTON && state == GLUT_DOWN) axis = 1;if(btn==GLUT_RIGHT_BUTTON && state == GLUT_DOWN) axis = 2;
}void display()
{glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);glLoadIdentity();glRotatef(theta[0], 1.0, 0.0, 0.0);glRotatef(theta[1], 0.0, 1.0, 0.0);glRotatef(theta[2], 0.0, 0.0, 1.0); colorcube();glutSwapBuffers();
}

注意，由于回调函数的参数形式是固定的，类似于theta和axis等变量必须定义为全局变换，照相机信息在标准的形状改变回调函数中定义。
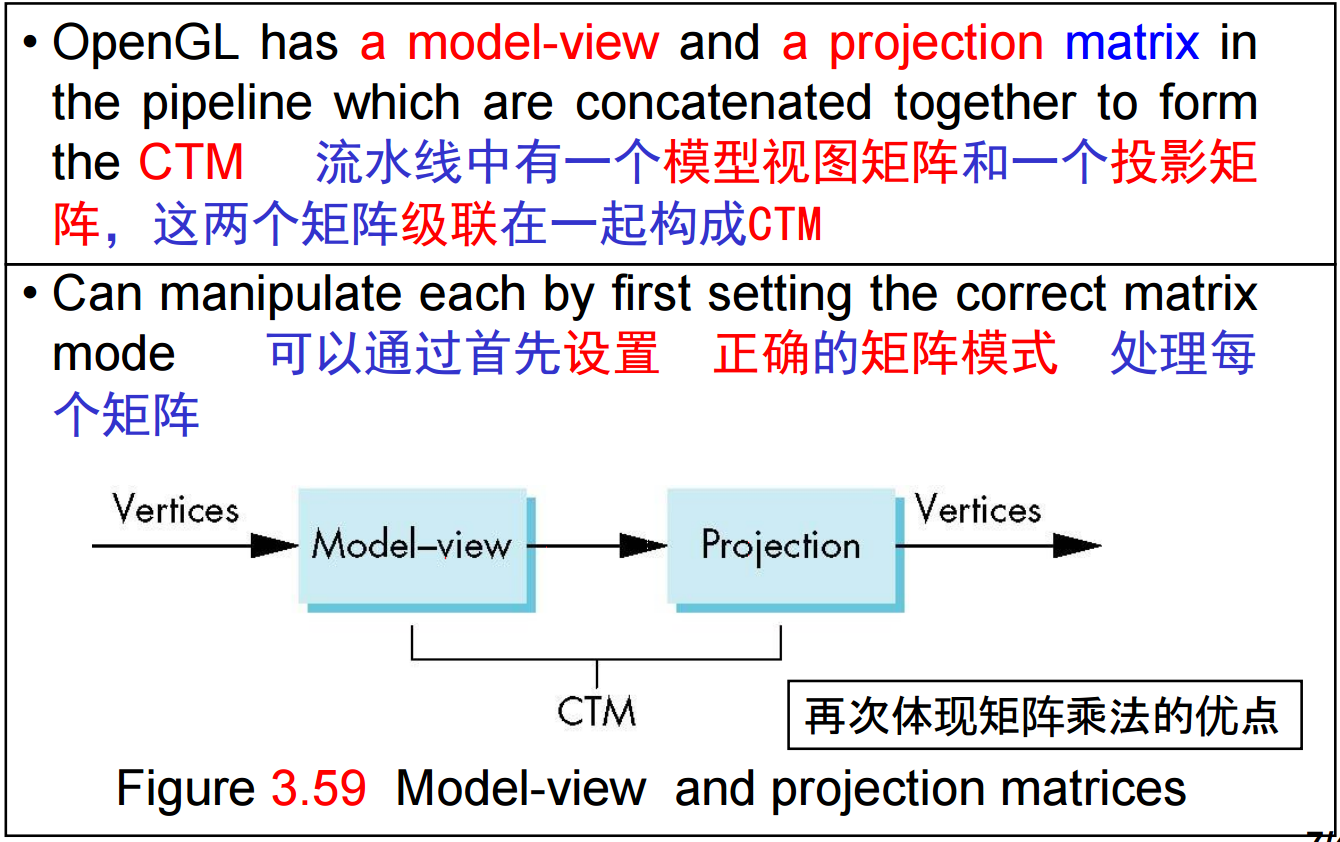
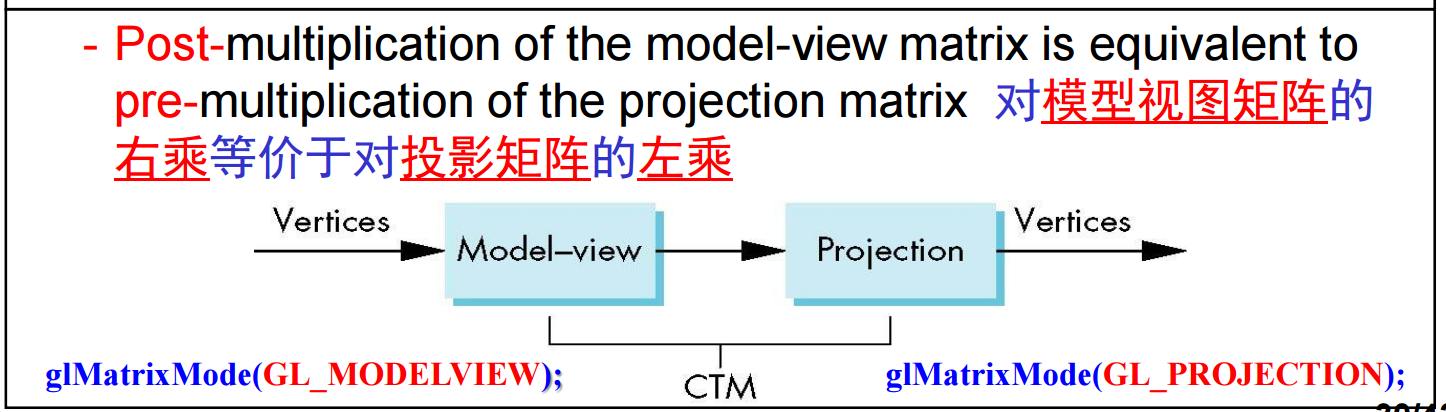
6、在OpenGL模型视图矩阵（model-view matrix）可以用来定位照相机（虽然可以利用旋转和平移实现，但采用gluLookat()会更简单直观）、建立对象模型。投影矩阵用来定义视景体以及选择照相机镜头。虽然两者有同样的函数进行处理，但应用时必须非常仔细，因为累加的改变总是右乘到CTM上。例如，用同样的旋转矩阵作用模型视图矩阵和投影矩阵并不是等价的操作：

7、交互计算机图形学的一个主要问题就是如何应用二维的设备（如鼠标）控制三维的对象？方法：①应用屏幕区域（根据不同的鼠标按钮状态，利用到中心点的距离控制角度、位置、放缩）；②Virtual trackball虚拟跟踪球；③三维输入设备。

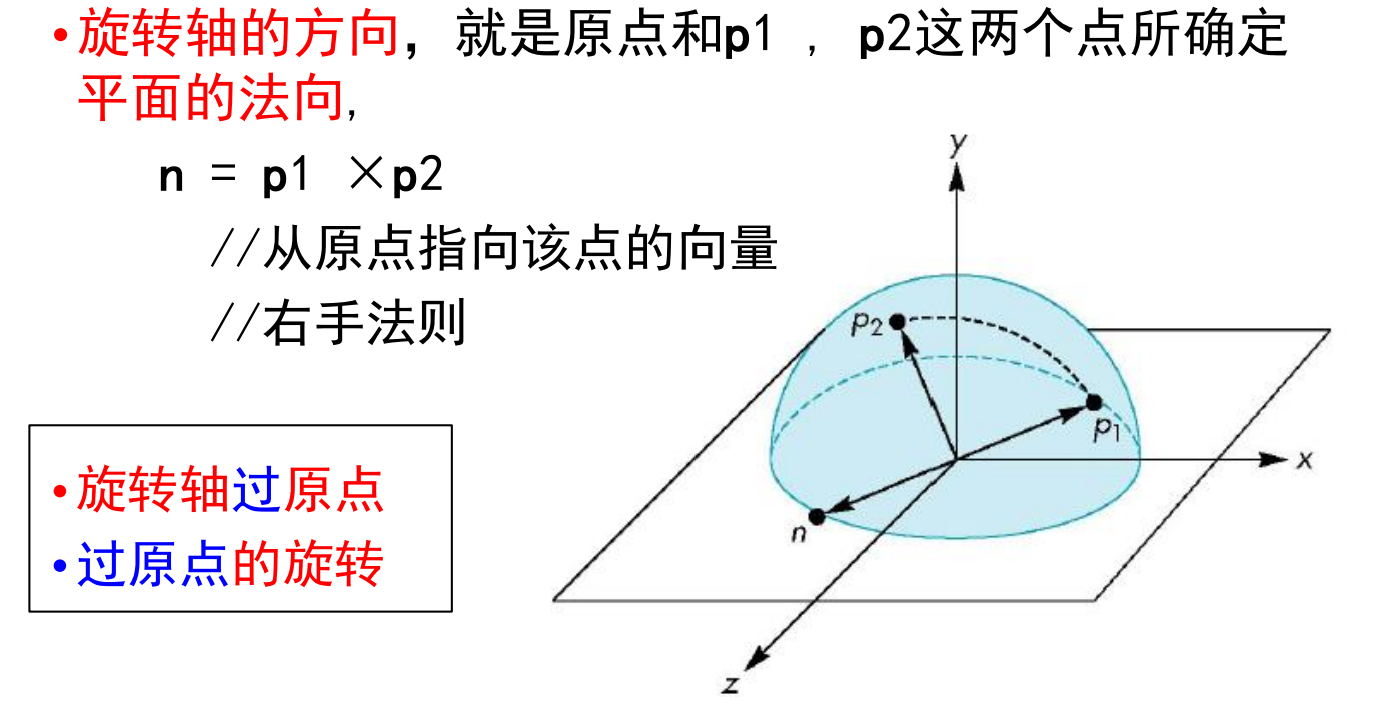
当我们从鼠标得到两个点，就可以把它们投影到半球面上的点p1和p2，这两个点确定了球面上的一个大圆，找到恰当的旋转轴和旋转角度就可以把p1旋转到p2，如下图：

8、 Smooth Rotation光滑旋转。①小增量方法：从实际的标准来看，需要通过变换来光滑移动和旋转一个对象，问题是给出一个模型视图矩阵列M0, M1, …, Mn使得当把它们作用到一个或多个对象上时，采用很小增量，但是用户观察来看，不光滑。②大圆方法：在定向对象时，可以利用一个事实，那就是任一旋转对应着球面上的大圆的一部分，那就只需求出旋转轴与角度即可（如虚拟跟踪球）。
9、前面两种途径对于一组旋转矩阵R0,R1,…..,Rn, f求出每个的Euler角，从而应用Ri= Riz Riy Rix不是很有效（不光滑）。利用最终的位置确定旋转轴与旋转角度，从而增加这个角度，光滑。四元数方法比上述两种方法都有效。四元数由威廉·卢云·哈密顿在1843年爱尔兰发现，把虚数从二维推广到了三维，需要一个实部和三个虚部i, j, k（q=q0+q1i+q2j+q3k），三个虚部正好对应一个向量。

四元数可以表示在球面上的光滑旋转，而且非常有效。处理过程为：①模型视图矩阵 → 四元数；②用四元数进行运算；③四元数 → 模型视图矩阵。