当前位置：首页 > news >正文

S13 排序算法--快速排序

news 2025/11/9 14:36:33

快速排序是数据结构中分治思想的经典应用，核心优势是平均时间复杂度低、原地排序、实际工程中效率高，是处理大规模数据的优选排序算法之一。

算法原理

快速排序的核心是「分而治之」：

选择基准值：从数组中选一个元素作为 “基准”（如数组第一个元素、最后一个元素、中间元素或随机元素）。
分区（partition）：重新排列数组，将所有比基准值小的元素放到基准值左边，比基准值大的元素放到右边（相等元素可放任意一侧），最终基准值落在其 “最终有序位置”。
递归排序：对基准值左侧的子数组和右侧的子数组，重复 “选择基准→分区→递归” 步骤，直到子数组长度为 1（天然有序）或 0（空数组）。

核心思路（以升序为例）

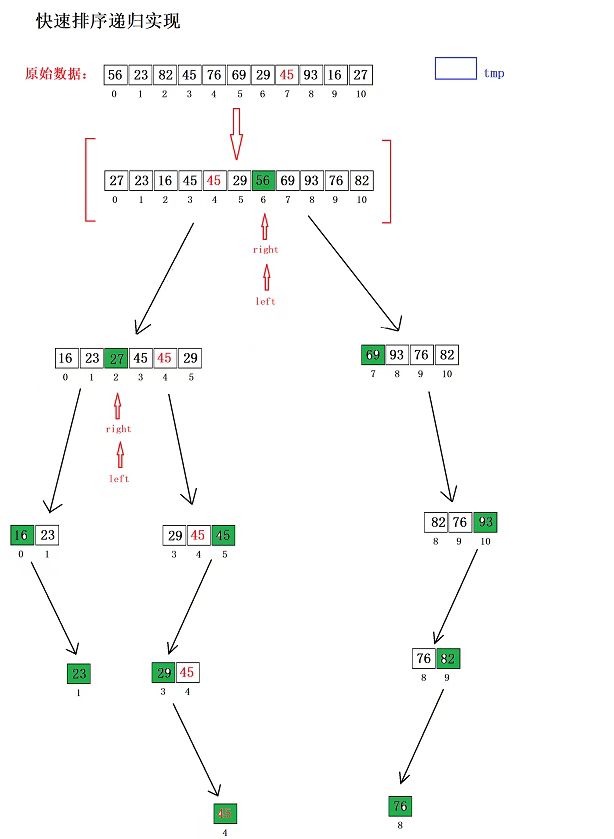
以数组 [56, 23, 82, 45, 76, 69, 29, 45, 93, 16, 27] 为例，步骤拆解：

low=0，high=10，mid=0+(10-0)/2=5
三数取中：比较 arr[0]=56、arr[5]=69、arr[10]=27 → 中间值为 56（arr[0]），基准值 pivot=56。

分区过程（目标：基准值 56 左侧＜56，右侧≥56）

初始化 i=0，j=10。

j 从右向左找＜56 的元素：arr[10]=27（满足），j=10。

i 从左向右找＞56 的元素：arr[0]=56（不满足）→ i=1（23）→ i=2（82，满足），i=2。

交换 arr[2]（82）和 arr[10]（27）→ 数组变为：[56, 23, 27, 45, 76, 69, 29, 45, 93, 16, 82]。

继续循环：j=9（16＜56，满足）；i=3（45＜56）→ i=4（76＞56，满足），i=4。

交换 arr[4]（76）和 arr[9]（16）→ 数组变为：[56, 23, 27, 45, 16, 69, 29, 45, 93, 76, 82]。

继续循环：j=8（93≥56）→ j=7（45＜56，满足）；i=5（69＞56，满足），此时 i=5 > j=7？不，i=5 < j=7，交换 arr[5]（69）和 arr[7]（45）→ 数组变为：[56, 23, 27, 45, 16, 45, 29, 69, 93, 76, 82]。

继续循环：j=6（29＜56，满足）；i=6（29＜56）→ i=7（69＞56，满足），此时 i=7 > j=6，循环终止。

基准值归位：交换 arr[0]（56）和 arr[6]（29）→ 数组变为：[29, 23, 27, 45, 16, 45, 56, 69, 93, 76, 82]。

基准值 56 的最终索引 pivotIdx=6，左侧子数组 [0~5]（[29,23,27,45,16,45]），右侧子数组 [7~10]（[69,93,76,82]）。

C 语言实现

1. 核心函数：分区函数（partition）

int partition(int*arr,int left,int right){int tmp=arr[left];int r=right+1;for(int i=right;i>left;i--){if(arr[i]>tmp){r--;arr[r]=arr[i];}}int t=arr[r-1];arr[r-1]=arr[left];arr[left]=t;
}

2.递归排序函数

通过分区结果递归排序左右子数组：

void QucikSort(int*arr,int left,int right){if(left<right){int index=partition(arr,left,right);QuickSort(arr,left,index-1);QucikSort(arr,index+1,right);}
}

3.三数取中法避免快速排序缺陷

int medianOfThree(int arr[], int low, int high) {int mid = low + (high - low) / 2;  // 避免溢出// 排序low、mid、high三个位置的元素，让mid成为中间值if (arr[low] > arr[mid]) swap(&arr[low], &arr[mid]);if (arr[low] > arr[high]) swap(&arr[low], &arr[high]);if (arr[mid] > arr[high]) swap(&arr[mid], &arr[high]);return mid;  // 返回中间值的索引（作为基准）
}

算法分析

1. 复杂度分析

时间复杂度	空间复杂度	稳定性
最好：O (n log n)	最好：O (log n)	不稳定
平均：O (n log n)	平均：O (log n)
最坏：O (n²)	最坏：O (n)

时间复杂度：平均情况下，每次分区将数组分成两个大致相等的子数组，递归深度为 O (log n)，每一层分区的时间为 O (n)，总时间 O (n log n)；最坏情况（基准值选得极差）递归深度为 O (n)，时间 O (n²)（优化后可避免）。

空间复杂度：主要来自递归栈，平均递归深度 O (log n)，最坏 O (n)（尾递归优化后可降至 O (log n)）。

稳定性：不稳定（分区时可能交换相等元素的位置，如[2, 1, 2]，基准值为第一个 2，交换后第二个 2 会到左边）。

2. 优缺点

核心优点	核心缺点
平均效率高（实际工程中比归并排序、堆排序快）	不稳定排序
原地排序（空间复杂度低，无需额外数组）	最坏时间复杂度 O (n²)（需优化规避）
对缓存友好（局部性好，适合大规模数据）	递归实现可能栈溢出（需尾递归优化）