Diffusion 到 Flow Matching ( 从 DDPM 到 Stable Diffusion ) 丝滑入门

第 1 部分：扩散模型 (Diffusion Models)

1.1 核心概念：模拟“破坏-修复”

扩散模型 (Diffusion Model) 是一类深度生成模型，其灵感来源于物理学中的扩散过程（比如墨水滴入水中）。

它的核心思想是模拟两个相反的过程：

• ① 正向扩散 (Forward Process - 破坏):

  • 这是一个固定的、无可学习参数的过程。
  • 它从一张干净的原始数据（如图像 $x_0$）出发，在 $T$ 个时间步中，逐步、迭代地向图像中添加高斯噪声。
  • 直到第 $T$ 步，图像 $x_T$ 变得几乎等同于纯粹的随机噪声。

• ② 反向扩散 (Reverse Process - 修复):

  • 这是模型真正学习的部分。
  • 模型（通常是一个 U-Net）的任务是逆转上述过程：从纯噪声 $x_T$ 开始，一步步地、迭代地去除噪声。
  • 经过 $T$ 步去噪后，模型应该能“修复”或“雕刻”出一张清晰的、符合原始数据分布的图像 $x_0$。

1.2 学习机制：一种特殊的“监督学习”

Diffusion 和 Flow Matching 本质上都是一种特殊的监督学习。

它们与传统监督学习（如分类）不同，它们监督的不是最终的“类别标签”，而是**“转换过程”本身**。它们是“以数据分布为目标的、高维的、基于回归的监督学习”。

• 监督目标 (GT) 是什么？

  • 在训练时，我们拿一张干净图片 $x_0$，随机选择一个时间步 $t$，并加入一个已知的、随机生成的精确噪声 $ϵ$ 得到带噪图 $x_t$。
  • 这个已知的噪声 $ϵ$ 就是我们要监督的“地面真相”(Ground Truth, GT)。

• 监督形式 (损失函数)：

  • 模型 ${ϵ}_{\theta }(x_t,t)$ 的任务就是输入带噪图 $x_t$ 和时间 $t$，然后预测出这个 $ϵ$。
  • 损失函数就是均方误差 (MSE)：
    $$L\propto ||ϵ-{ϵ}_{\theta }(x_t,t)|{|}^2$$
  • 这本质上就是一个回归任务：模型被训练去回归（预测）那个我们事先知道的、用来“破坏”数据的噪声 $ϵ$。

• 对比 Flow Matching：

  • Flow Matching 也是同样的逻辑，但它监督的是**“瞬时速度”**。
  • GT 是理论上从噪声导向数据的精确速度向量 $v(x_t,t)$。
  • 损失函数是 $L\propto ||v-v_{\theta }(x_t,t)|{|}^2$。

1.3 记忆载体：U-Net 的权重

模型的“记忆”，即它对数据分布（如猫的形状、纹理、结构）的所有知识，绝大部分都集中在 U-Net 的权重中。

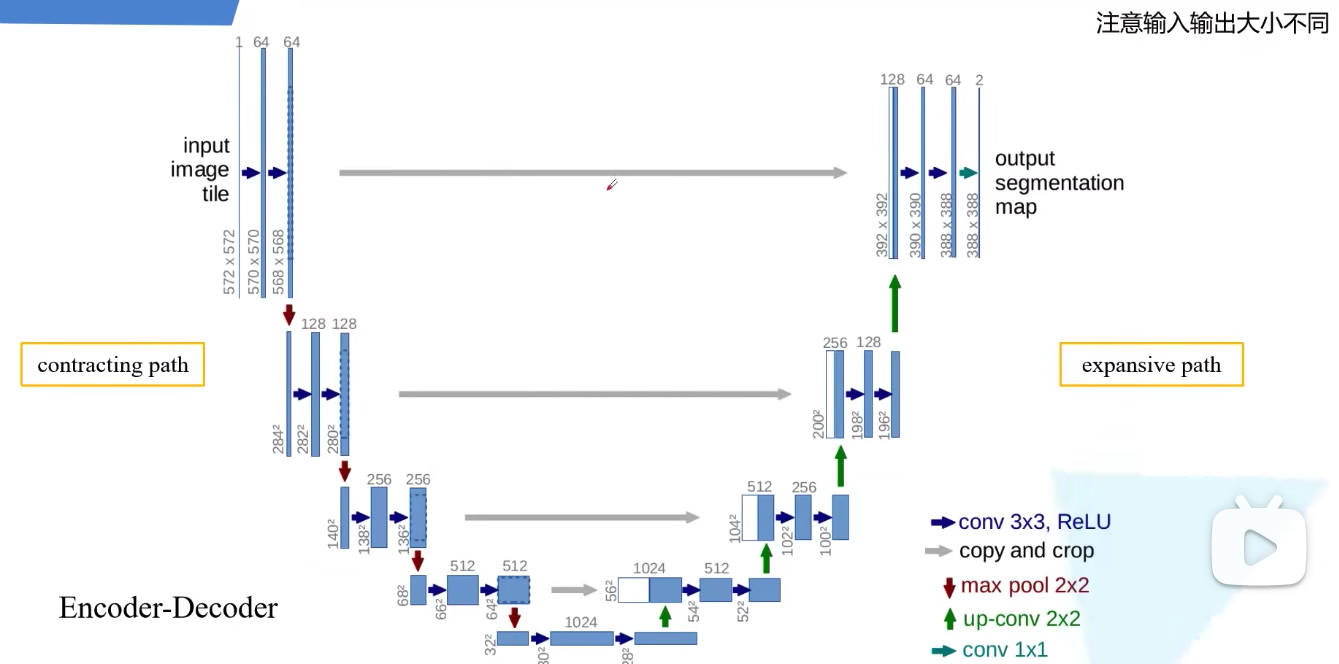
这个 U-Net 的结构非常特别，完美地执行了“噪声预测”这个回归任务：

• 输入： 带噪图像 $x_t$ (如 64x64x3) + 时间嵌入 $t$。
• 1. 编码器 (Encoder / 下采样):
  • U-Net 的前半部分通过卷积和池化，将高维（大尺寸、少通道）的图像压缩成低维（小尺寸、多通道）的特征图。
  • 例如，从 64x64x3 逐步压缩到 8x8x512。
  • 这一步是为了提取图像的抽象语义特征。
• 2. 解码器 (Decoder / 上采样):
  • U-Net 的后半部分通过反卷积或上采样，将低维特征图逐步还原回高维图像。
  • 例如，从 8x8x512 逐步还原到 64x64x3。
  • 这一步是为了恢复图像的细节。
• 3. 跨层连接 (Skip Connections):
  • 这是 U-Net 的精髓。它将编码器中（浅层、高分辨率）的特征图“跳过”并直接添加到解码器对应的层上。
  • 这确保了模型在还原图像时，不会丢失精细的细节和纹理。
• 输出： 预测的噪声 ${ϵ}_{\theta }$ (尺寸与输入 $x_t$ 完全相同，如 64x64x3)。

1.4 关键机制：时间步 (类 RNN 循环)

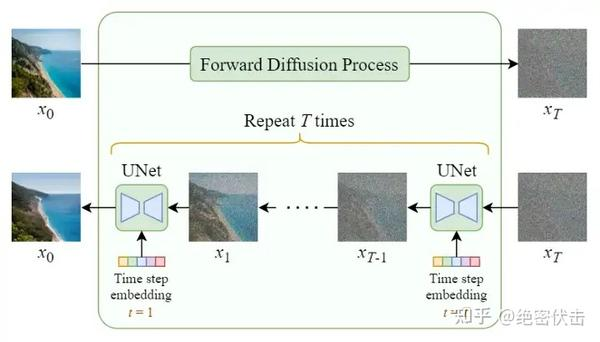
U-Net 像 RNN 是非常精辟的比喻。它在两个方面区别于传统的网络：

• 1. 参数共享 (像 RNN)：

  • 传统的编码器-解码器，每一层都是独立学习的。
  • 而 Diffusion Model 只使用一个 U-Net，并在所有 $T$ 个时间步中共享同一套参数。
  • 在**推理（生成）**阶段，模型会从 $t=T$ 到 $t=0$ 循环调用这个固定的 U-Net。

• 2. 时间嵌入 (Time Embedding)：

  • 问题： 既然是同一套 U-Net 权重，它如何知道自己当前处于哪个时间步？（例如，$t=999$ 时应大刀阔斧去噪，而 $t=10$ 时应精细修饰）。
  • 答案： 我们把时间步 $t$ 作为一个额外的输入。
  • $t$ 通常被编码为一个高维向量（使用正弦/余弦位置编码），这个“时间嵌入”被深度融入到 U-Net 的每一个残差块和注意力层中。
  • 作用： 告诉 U-Net “现在循环到哪一步了”，使其能够根据当前进度动态调整关注点（例如，早期关注整体结构，晚期关注细节）。

重要贡献： 原始的扩散模型 [NIPS 2015] 表现不佳。而 DDPM [NeurIPS 2020] 作为“开山之作”，其一大贡献就是系统性地阐述了这种“时间嵌入”对于共享参数的 U-Net 的重要性，并证明了只学习均值（预测噪声 $ϵ$）就足够了。

1.5 综合实例：“监督”一只猫的生成

目标： 训练 U-Net ${ϵ}_{\theta }$ 学会从噪声中还原出猫。

一次训练迭代 (Training Step)：

1. 准备数据： 从数据集中取一张清晰的猫图 $x_0$。
2. 制造“监督数据对”： 随机抽取几个时间步 $t$ 和几个高斯噪声 $ϵ$。
   • 样本 A (t=999):
     • 输入： $x_0$ + 99.9% 的已知噪声 ${ϵ}_A$ $\to$ 得到 $x_{999}$ (几乎纯噪声)。
     • GT 标签： ${ϵ}_A$。
   • 样本 B (t=500):
     • 输入： $x_0$ + 50% 的已知噪声 ${ϵ}_B$ $\to$ 得到 $x_{500}$ (中度噪声)。
     • GT 标签： ${ϵ}_B$。
   • 样本 C (t=100):
     • 输入： $x_0$ + 10% 的已知噪声 ${ϵ}_C$ $\to$ 得到 $x_{100}$ (轻微噪声)。
     • GT 标签： ${ϵ}_C$。
3. 模型预测与监督 (计算损失)：
   • 对于样本 A (t=999):
     • 模型计算：${ϵ}_{pred\_A}={ϵ}_{\theta }(x_{999},t=999)$。
     • 计算损失：$L_A=||{ϵ}_A-{ϵ}_{pred\_A}|{|}^2$。
     • 模型学习： 从一团混沌中找到最微弱的“猫”的结构痕迹。这是创造力和多样性的来源，因为模型学会了应对任何随机噪声起点。
   • 对于样本 B (t=500):
     • 模型计算：${ϵ}_{pred\_B}={ϵ}_{\theta }(x_{500},t=500)$。
     • 计算损失：$L_B=||{ϵ}_B-{ϵ}_{pred\_B}|{|}^2$。
     • 模型学习： 在大量噪声中识别出猫的宏观结构和轮廓。
   • 对于样本 C (t=100):
     • 模型计算：${ϵ}_{pred\_C}={ϵ}_{\theta }(x_{100},t=100)$。
     • 计算损失：$L_C=||{ϵ}_C-{ϵ}_{pred\_C}|{|}^2$。
     • 模型学习： 学习如何修复精细的细节，如胡须、毛发纹理。

通过在所有 $t$ 上最小化这个损失，U-Net 的权重（记忆）最终被迫学会了从 $t=T$ (纯噪声) 到 $t=0$ (清晰图像) 的完整“修复”路径图。

---

第 2 部分：条件控制 (Conditional Diffusion)

在第一部分中，我们训练的 U-Net 是一个“盲盒”生成器。它从随机噪声出发，能生成一张高质量的猫图，但我们无法控制生成 什么样 的猫。

问题： 如果我想“干预”这个过程，让模型听我的话，比如生成“一只红色的猫”或“一只宇航员在骑马”，该怎么做？

这就是条件控制 (Conditional Control) 要解决的问题，是连接 DDPM（纯生成）和 Stable Diffusion（可控生成）的核心桥梁，也是 Stable Diffusion 的核心原理。

2.1 核心思想：为 U-Net 引入“导航”

我们不能改变 U-Net 的核心任务（预测噪声 ${ϵ}_{\theta }$），但我们可以在它工作时，给它提供“导航信息”。

想象一下，U-Net 就像一个正在雕刻大理石的工匠（从噪声 $x_T$ 雕刻到图像 $x_0$），而“文本提示 (Prompt)”就是我们递给工匠的图纸。

挑战： U-Net 只“认识”两样东西：

1. 带噪声的图像 $x_t$ (它要处理的“大理石”)
2. 时间步 $t$ (它要知道雕刻到哪一步了)

U-Net 根本不认识“文本”这种高级语义。

解决方案 (Stable Diffusion 采用)：

1. 找一个“翻译官”，把人类的文本“翻译”成 U-Net 能理解的数学语言（向量）。
2. 在 U-Net 内部开几个“小窗户”，让“翻译”后的信息（图纸）能在关键时刻递给工匠。

这个“翻译官”就是文本编码器 (Text Encoder)，而这个“小窗户”就是交叉注意力 (Cross-Attention) 机制。

2.2 具体例子：“一只戴帽子的宇航员猫”

我们来完整地走一遍，当 U-Net 收到这个提示 (Prompt) 时，内部发生了什么。

步骤 1：文本“翻译” (Text Encoder)

首先，我们不能把“宇航员猫”这几个字直接扔给 U-Net。

1. 分词 (Tokenize): 文本被分解成一个个“词元”(Token)。
   "A", "cat", "astronaut", "wearing", "a", "hat"
2. 编码 (Encode): 这些词元被送入一个专门的、预训练好的文本编码器（例如 CLIP Text Encoder）。
3. 输出 (Embedding): 编码器输出一系列的上下文向量 (Context Vectors)，$C$。
   • $C_1$ (代表 “A”)
   • $C_2$ (代表 “cat”)
   • $C_3$ (代表 “astronaut”)
   • …
   • 关键： 这一系列向量 $C$ 蕴含了提示词的全部语义。这就是我们的“图纸”。

步骤 2：“干预” U-Net (Cross-Attention)

现在，U-Net 开始像往常一样工作（从 $t=T$ 循环去噪）。

1. 常规路径 (图像侧): 在某个时间步 $t$，带噪图像 $x_t$ 进入 U-Net 的编码器（下采样）。在 U-Net 的中间层，图像被压缩成了一堆图像特征（$Q$）。

   • $Q$ (Query / 查询): 可以理解为 U-Net 内部的“提问”。比如，图像特征 $Q_i$ 在“提问”：“我这块区域（比如图像左上角）应该生成什么东西？”

2. 干预路径 (文本侧): 我们把上一步得到的上下文向量 $C$ 作为“回答”的候选。

   • $K$ (Key / 键): $C$ 向量充当“键”，代表每个词的“身份”。
   • $V$ (Value / 值): $C$ 向量也充当“值”，代表每个词的“内容”。

3. 交叉注意力 (Q, K, V 匹配):

   • U-Net 的图像特征 $Q_i$（“我这块区域要画啥？”）会和所有文本词元 $K$（$K_{cat},K_{astronaut},K_{hat}$…）进行匹配度计算。
   • 假设： 如果 $Q_i$ 这个区域在之前的去噪中已经隐约呈现出“猫头”的轮廓，那么它与 $K_{hat}$ (“帽子”) 的匹配度就会非常高。
   • 结果： 匹配度最高的 $K_{hat}$ 对应的 $V_{hat}$（“帽子”的内容）就会被选中，并被注入 (Inject) 到 $Q_i$ 中，成为新的图像特征。

执行过程（类比）：

• t=990 (混沌期): U-Net 问：“这里一团糟，我该画啥？” $\to$ 文本 $C$ 回答：“画个‘宇航员’和‘猫’的轮廓。”
• t=500 (轮廓期): U-Net 问：“我画出了一个猫头，上面这块是啥？” $\to$ 交叉注意力机制发现 $Q_{猫头上}\cdot K_{hat}$ 匹配度最高 $\to$ 注入 $V_{hat}$ 的信息 $\to$ U-Net 开始在猫头上画“帽子”。
• t=10 (细节期): U-Net 问：“帽檐这里要什么纹理？” $\to$ 交叉注意力再次注入 $V_{hat}$ 的细节信息 $\to$ U-Net 精修帽檐。

总结：
交叉注意力，就是在 U-Net 内部（通常是其中间层和解码器层）加入的“导航站”。在去噪的每一步，U-Net 都会停下来，通过这个机制“看一眼”文本图纸，让图像特征和文本语义对齐，然后再继续下一步去噪。

2.3 关键技巧：Classifier-Free Guidance (CFG)

我们已经“干预”了 U-Net，但还有一个问题：U-Net 有多“听话”？

有时候，模型可能“偷懒”，它更倾向于生成它最熟悉的（比如一张普通的猫），而不是你想要的（戴帽子的宇航员猫）。

CFG (无分类器指导) 是一个强大的技巧，用来控制模型对提示词的“遵从度”。

原理： 在每一步 $t$，我们实际上让 U-Net 做了两次噪声预测：

1. 预测 1 (有条件): ${ϵ}_{\theta }(x_t,t,\text{"宇航员猫"})$
   • 即我们刚刚描述的、受交叉注意力“干预”的预测。
2. 预测 2 (无条件): ${ϵ}_{\theta }(x_t,t,\text{""})$
   • 我们用一个空的、无意义的提示词（或干脆去掉干预），让 U-Net “自由发挥”，预测它最想画的东西（比如一张普通的猫）。

计算：

• 我们得到了两个预测：${ϵ}_{cond}$ (你想要的) 和 ${ϵ}_{uncond}$ (它想画的)。
• 指导方向： $({ϵ}_{cond}-{ϵ}_{uncond})$ 这个向量，指向了从“普通猫”到“宇航员猫”的“进化方向”。

最终预测：
$${ϵ}_{final}={ϵ}_{uncond}+w\times ({ϵ}_{cond}-{ϵ}_{uncond})$$

• $w$ 就是指导系数 (Guidance Scale)。
• $w=0$： ${ϵ}_{final}={ϵ}_{uncond}$ (完全不听提示，自由发挥)。
• $w=1$： ${ϵ}_{final}={ϵ}_{cond}$ (标准干预)。
• $w>1$ (如 7.5)： 我们在“普通”的基础上，超量地、夸张地加上了“宇航员猫”的特征。这迫使 U-Net 必须严格遵从提示词，生成更贴合、更鲜明的结果。

---

小结：

U-Net 依然是那个基于回归的噪声预测器（第一部分的核心）。而条件控制（Stable Diffusion）的魔法在于：

1. 使用 Text Encoder 将提示词“翻译”成 $C$ 向量。
2. 在 U-Net 内部加入 Cross-Attention 层，在每一步 $t$ 都将图像 $Q$ 和文本 $K,V$ 对齐，实现“干预”。
3. 使用 CFG 技巧，通过对比“有条件”和“无条件”的预测，放大提示词的影响力，让 U-Net 严格“听话”。

---

第 3 部分：新范式——作为“生成式监督”的 Diffusion

为什么 Diffusion 和 Flow Matching 这类技术正迅速成为 VLA（视觉-语言-动作）和模仿学习（Imitation Learning）领域“动作专家（Action Experts）”或“策略（Policy）”的首选监督框架？

在第 1 部分和第 2 部分，我们明确了 U-Net 是如何通过“回归噪声”来学习整个数据分布的。现在，我们拔高一个层次，探讨一个核心观点：

Diffusion 不是一个传统的“监督头”，它是一种“生成学习框架”。

3.1 传统监督头 vs. 生成式监督框架

我们先来做一个对比，以 模仿学习（Imitation Learning） 中的“动作预测”为例。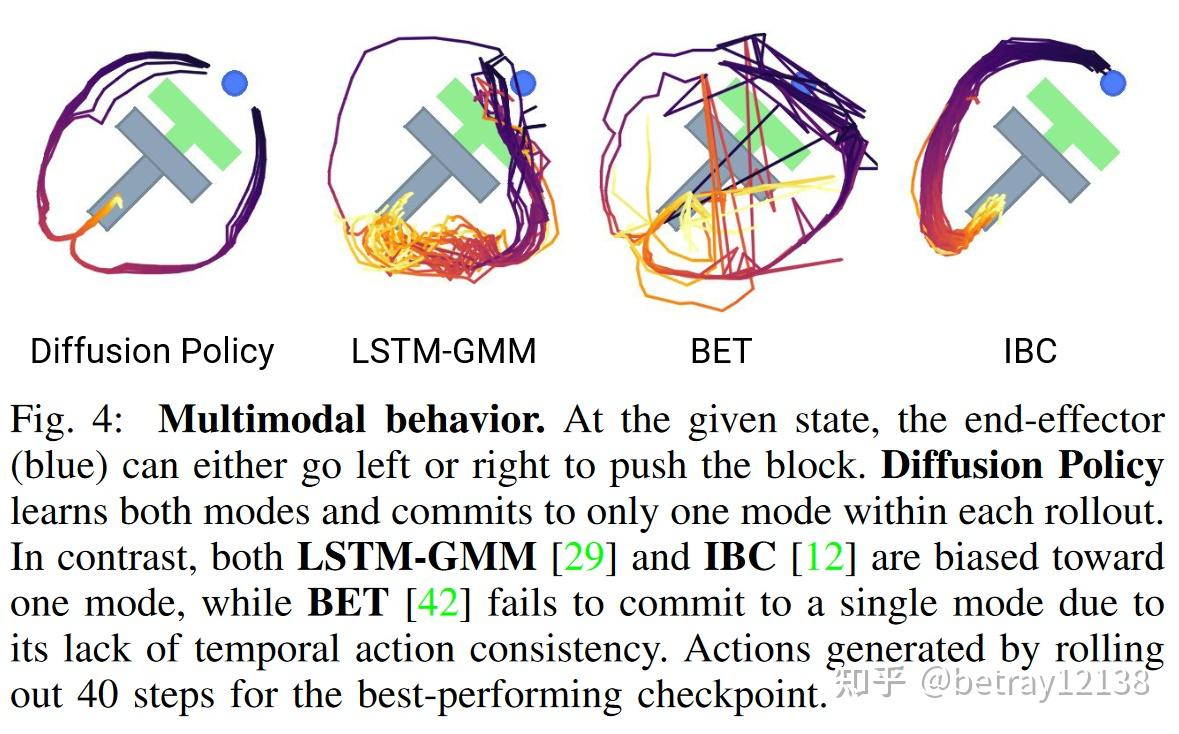
上图中的行为克隆（BC）就是一种监督学习/模仿学习；LSTM 是一种可适配 L2 自回归的模型；

模仿学习的目标： 学习一个策略，根据当前的“观察”（Observation，如图像、语言指令），预测出机器人下一步应该执行的“动作”（Action，如关节角度、末端轨迹）。

传统监督头 (如 L2 回归)：

• 做法： 假设我们有 1000 个人类演示（GT 轨迹）。在某个相同状态 $S$ 下，人类 A 走了轨迹 $A$，人类 B 走了轨迹 $B$。
• 模型： 一个简单的回归头（如 MLP）被训练来最小化预测动作 $a_{pred}$ 和真实动作 $a_{GT}$ 之间的 L2 损失（均方误差）。
• 问题 (模式平均 Mode Averaging)：
  • 为了最小化在 $A$ 和 $B$ 上的平均损失，这个“笨拙”的回归头最终会学会预测一个介于 $A$ 和 $B$ 之间的、物理上不存在的“折衷”动作 $C$。
  • 这个动作 $C$ 既不是 $A$ 也不是 $B$，它可能是一个无效、抖动或不自然的动作。
• 结论： 传统回归头无法处理“多样性”。它假设在同一输入下只有一个正确答案，当存在多个正确答案时，它会崩溃并输出所有答案的平庸平均值。

生成式监督框架 (Diffusion / Flow Matching)：

• 做法： 我们同样用这 1000 个演示 $A,B,...$ 来训练。
• 模型： 我们训练一个 Diffusion Policy (或 Flow Policy)。这个模型学习的不是“预测一个动作”，而是学习 $P(Action|Observation)$ 这个“概率分布”本身。
• 监督信号： 正如第 1 部分所述，它的损失函数是“回归噪声”或“回归速度”。
• 优势 (解决多样性)：
  • Diffusion 框架被迫学习整个分布。它在训练中看到过轨迹 $A$（通过去噪 ${ϵ}_A$），也看到过轨迹 $B$（通过去噪 ${ϵ}_B$）。
  • 它不会去“平均” $A$ 和 $B$。相反，它在自己的权重（U-Net）中记住了：从 $S$ 出发，有两条“合法”的去噪路径，一条通往 $A$，一条通往 $B$。
• 结论： Diffusion 完美地解决了“创造性 (Creativity)” 和 “多样性 (Diversity)” 的监督问题。它承认在同一情境下，存在多种同样“正确”的解决方案。

3.2 具体例子：VLA 中的“动作专家” (Diffusion Policy)

让我们看看这在 VLA 模仿学习中是如何具体应用的。

场景： 一个机器人手臂需要根据指令“请把那个红苹果递给我”来规划未来 2 秒的动作轨迹（Action Horizon）。

• Observation (输入): 摄像头图像 + 文本指令 “…”。
• Action (GT 标签): 人类专家演示的 2 秒钟（例如 100 帧）的关节角度序列 $A_{GT}$。这是一个高维向量（例如 100 帧 x 7 关节）。

传统回归头 (失败)：
如果用 L2 损失，模型会试图预测一个“平均”的轨迹。如果专家演示时，一半是从左边抓，一半是从右边抓，模型会预测一个从中间穿过去的、撞到桌子的轨迹。这导致了创造力的缺失。

Diffusion Policy (成功)：

1. 训练 (监督过程)：

   • 我们拿到 GT 轨迹 $A_{GT}$。
   • 像第 1 部分一样，我们加入随机噪声 $ϵ$，得到带噪轨迹 $A_t$。
   • U-Net 的任务： 输入 (Observation, $A_t$, $t$)，预测 $ϵ$。
   • 损失函数： $L=||ϵ-{ϵ}_{\theta }(\text{Observation},A_t,t)|{|}^2$。
   • 关键： 这里的 Observation（图像+文本）扮演了第 2 部分中“条件控制”的角色。它通过交叉注意力机制被注入 U-Net，指导 U-Net 的去噪方向。

2. 推理 (生成动作)：

   • 我们从一个完全随机的噪声轨迹 $A_T$（未来 2 秒的随机抖动）开始。
   • 我们输入当前的 (Observation)。
   • 模型（U-Net）从 $t=T$ 循环到 $t=0$，在 Observation 的强力引导下，一步步地将这个“随机抖动” $A_T$ “雕刻”成一条清晰、平滑、且多样化的动作轨迹 $A_0$。
   • 多样性的体现： 每次我们从不同的随机噪声 $A_T$ 开始，模型就会生成一条不同的、但同样合理的轨迹（比如，这次从左边抓，下次从右边抓）。

小结：

Diffusion 和 Flow Matching 不是简单的“监督头”，它们是高维概率分布的建模框架。

它们通过其独特的“回归噪声/速度”损失函数，迫使模型学习数据分布中的所有模式（Modes），而不是像 L2 损失那样崩溃为平庸的平均值。

这使得它们成为监督 VLA 动作专家这类具有“创造性”和“多样性”（即多模态，Multi-Modal）输出的完美工具。

---

第 4 部分：演变——从 Diffusion 的“随机阶梯”到 Flow Matching 的“直线高速”

在第 3 部分，我们确定了 Diffusion 是一种强大的“生成式监督”框架。但它有一个（曾经）臭名昭著的缺点：慢。

• Diffusion (DDPM)：需要 $T$ 步（比如 1000 步）才能从纯噪声 $x_T$“雕刻”回 $x_0$。这意味着一次推理（生成）需要调用 1000 次 U-Net。
• Flow Matching：它的出现，很大程度上是为了解决这个问题。它旨在学习一个更“高效”的路径。

4.1 核心区别：随机 SDE vs. 确定性 ODE

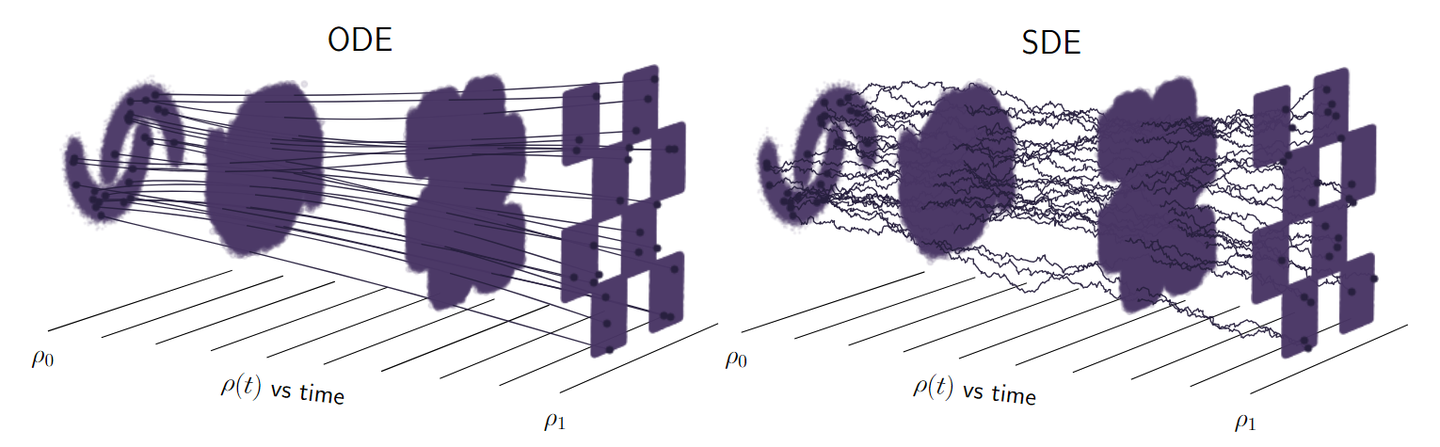
上图来源/进阶推荐：https://zhuanlan.zhihu.com/p/4116861550

• Diffusion (DDPM/SDE)： 它的反向过程（修复）是随机的 (Stochastic)。每一步 $t$ 不仅要预测 $ϵ$，还要在结果上再加一点点“随机噪声”。

  • 比喻：一个喝醉的工匠在走楼梯。
  • 他知道总目标是“下楼”（去噪）。
  • 但他每走一步（$t\to t-1$），都会左摇右晃（加入随机性）。
  • 他最终还是能下楼（生成图像），但这个路径是摇摇晃晃的、低效的。

• Flow Matching (ODE)： 它学习的是一个确定的 (Deterministic) 路径。

  • 比喻：一部在轨道上运行的电梯（或一条直线高速）。
  • 它学习的是一个“速度场 (Vector Field)” $v$。
  • 在任何时间 $t$、任何位置 $x_t$，这个 $v$ 都会给出一个唯一的、确定的“下一步该走的方向”。
  • 从 $t=1$ (噪声) 到 $t=0$ (数据) 的路径是平滑且笔直的。

4.2 终极具体实例：从 (0, 0) 移动到 (8, 8)

想象一下，我们的整个“数据分布” $x_0$ 只有一个点：坐标 (8, 8)。
我们的“噪声分布” $x_1$ 只有一个点：坐标 (0, 0)。

我们的任务是训练一个模型，学会如何从 (0, 0) 生成 (8, 8)。

---

A. Diffusion 的训练与推理（随机阶梯）

训练：

1. 取数据 $x_0$： (8, 8)。
2. 正向“破坏”： 我们把 (8, 8) $\to$ (0, 0) 的过程分成 10 步。我们模拟一个摇摇晃晃走向 (0, 0) 的过程。
3. 准备监督对：
   • 在 $t=5$ (中途)，数据点 $x_5$ 可能在 (4.1, 3.8)。
   • 我们加入的“真实噪声” ${ϵ}_A$ 是 (0.2, -0.3)。
   • 监督对 1： 输入 $x_5=(4.1,3.8)$ 和 $t=5$，GT 标签是 ${ϵ}_A=(0.2,-0.3)$。
   • 在 $t=3$，数据点 $x_3$ 可能在 (6.0, 5.8)。
   • 我们加入的“真实噪声” ${ϵ}_B$ 是 (-0.1, 0.1)。
   • 监督对 2： 输入 $x_3=(6.0,5.8)$ 和 $t=3$，GT 标签是 ${ϵ}_B=(-0.1,0.1)$。
4. 损失： $L=||ϵ-{ϵ}_{\theta }(x_t,t)|{|}^2$。

推理（生成）：

1. 启动： 从 $x_{10}=(0,0)$ 开始。
2. 第 1 步 (t=10)：
   • 模型预测 ${ϵ}_{\theta }(x_{10},10)$ $\to$ 比如 (0.7, 0.9)。
   • 我们计算 $x_9$ = (0, 0) + (0.7, 0.9) + 一点随机噪声 $\to$ 得到 $x_9=(0.8,0.85)$。
3. 第 2 步 (t=9)：
   • 模型预测 ${ϵ}_{\theta }(x_9,9)$ $\to$ 比如 (0.8, 0.7)。
   • 我们计算 $x_8$ = (0.8, 0.85) + (0.8, 0.7) + 一点随机噪声 $\to$ 得到 $x_8=(1.5,1.6)$。
4. …
5. 第 10 步 (t=1)：
   • 模型预测 ${ϵ}_{\theta }(x_1,1)$ $\to$ …
   • 最终得到 $x_0\approx (8.1,7.9)$。

结论： 我们到达了 (8, 8)，但走了 10 步，而且因为每一步的随机性，路径是弯曲的。

---

B. Flow Matching 的训练与推理（直线高速）

训练：

1. 取数据 $x_0$： (8, 8)。取噪声 $x_1$： (0, 0)。
2. 定义“高速公路”： 从 $x_1$ 到 $x_0$ 的直线路径。
3. 定义“速度 GT”： 在这条直线上，从起点 (0, 0) 指向终点 (8, 8) 的速度向量 (Velocity Vector) 是什么？
   • 答案是恒定的：$v_{GT}=x_0-x_1=(8,8)-(0,0)=(8,8)$。
   • 这个 $v_{GT}$ 就是我们要监督的唯一目标。
4. 准备监督对：
   • 随机取一个时间 $t=0.3$： * 在直线路上的 $x_t$ 是：$x_t=(1-t)x_1+t\cdot x_0=0.7\cdot (0,0)+0.3\cdot (8,8)=(2.4,2.4)$。
   • 监督对 1： 输入 $x_t=(2.4,2.4)$ 和 $t=0.3$，GT 标签是 $v_{GT}=(8,8)$。
   • 随机取一个时间 $t=0.8$：
     • 在直线路上的 $x_t$ 是：$x_t=0.2\cdot (0,0)+0.8\cdot (8,8)=(6.4,6.4)$。
   • 监督对 2： 输入 $x_t=(6.4,6.4)$ 和 $t=0.8$，GT 标签是 $v_{GT}=(8,8)$。
5. 损失： $L=||v_{GT}-v_{\theta }(x_t,t)|{|}^2=||(8,8)-v_{\theta }(x_t,t)|{|}^2$。模型 $v_{\theta }$ 被迫在高速公路上的任何一点，都要能预测出那个恒定的、指向终点的速度 (8, 8)。

推理（生成）：

1. 启动： 从 $x_1=(0,0)$ 开始。
2. 询问模型： $v_{\theta }(x_1,1.0)$？
3. 模型回答： （理想情况下） $v=(8,8)$。
4. 求解 ODE：
   • 如果我们想一步到位 (Rectified Flow)：
     • $x_0=x_1+1.0\times v=(0,0)+(8,8)=(8,8)$。
     • 一步！ 我们只调用了 1 次模型就完成了生成。
   • 如果我们想更精确（走 10 步）：
     • $x_{0.9}=x_1+0.1\times v=(0,0)+0.1\times (8,8)=(0.8,0.8)$。
     • $x_{0.8}=x_{0.9}+0.1\times v=(0.8,0.8)+0.1\times (8,8)=(1.6,1.6)$。
     • …
     • 最终 $x_0=(8,8)$。

结论： 我们不仅能一步到达 (8, 8)，而且即使分 10 步走，走的也是一条笔直的、确定的高速公路，没有任何随机性。

4.3 对 VLA 模仿学习的启示

• Diffusion (第 3 部分)： 它能学习多模态动作（多样性）。但它需要 100 步推理才能规划一个动作，这对于实时机器人来说太慢了。
• Flow Matching (演变)：
  • 它同样能学习多模态动作（如果 $x_0$ 是一个分布）。
  • 但它学习的是一个“确定性”的路径，使其推理速度极快。
  • 训练一个 Flow Matching 策略，模型 $v_{\theta }(\text{Observation},A_t,t)$ 学习预测从“随机动作” $A_1$ 指向“专家动作” $A_0$ 的速度 $v_{GT}=A_0-A_1$。
  • 在推理时，机器人只需调用模型 1-4 次，就能从随机噪声 $A_1$ 和速度 $v$ 计算出 $A_0=A_1+v$，从而规划出未来 2 秒的完整动作。
  • 这就是实现实时、高水平模仿学习的关键。