当前位置：首页 > news >正文

【二叉搜索树】：程序的“决策树”，排序数据的基石

news 2025/11/9 6:41:17

前言：终于来更新了，这几天一直在赶进度，这些底层的东西听懂加实现需要很长时间，大家在看完之后一定要自己动手，要不然白学，接下来四篇学的内容都是面试与笔试的高频考点，小伙伴们要重视起来哦。看这几篇之前，这篇“【二叉树与堆】：从“根”本说起，一起爬满数据的枝桠！”一定要学会哦！

一、二叉搜索树的概念

二、二叉搜索树的实现

1. ⼆叉搜索树的插⼊

2.⼆叉搜索树的查找

3. ⼆叉搜索树的删除

三、二叉搜索树的应用模型

1. Key模型（纯关键词搜索）

2. Key/Value模型（关键词与对应值）

四、二叉搜索树的性能分析

五、二叉树进阶算法题

1. 根据二叉树创建字符串

2. 正向层序遍历

3. 反向层序遍历

4. 最近公共祖先

5. 从前序/后序与中序遍历序列构造二叉树

6. 非递归前序遍历/中序遍历

7. 非递归后序遍历

8. 将二叉搜索树转化为排序的双向链表

一、二叉搜索树的概念

二叉搜索树，也称为二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树：

若它的左子树不为空，则左子树上所有节点的值都小于等于根节点的值

若它的右子树不为空，则右子树上所有节点的值都大于等于根节点的值

它的左右子树也分别为二叉搜索树

（所有节点！所有节点！不是只有它的孩子那一个结点符合大小关系！）

简单来说，它就像一个有严格家规的家族：每个节点的左孩子都比自己小（或相等），右孩子都比自己大（或相等）。

注意点：

二叉搜索树可以支持插入相等的值，也可以不支持，具体取决于使用场景。我们后续要学习的C++ STL容器中，map和set不支持插入相等键值，而multimap和multiset支持。

二、二叉搜索树的实现

树的结构还和以前一样

template<class T>
struct BTNode
{T _key;BTNode<T>* _left;BTNode<T>* _right;BTNode(const T& key):_key(key), _left(nullptr), _right(nullptr){}
};

1. ⼆叉搜索树的插⼊

插入过程遵循一个简单的原则：“比大小，找位置”：

树为空：直接创建新节点作为根节点。

树不为空：从根开始，将插入值与当前节点比较：

插入值大于当前节点值 → 往右子树走

插入值小于当前节点值 → 往左子树走

插入值等于当前节点值（且允许重复）→ 按约定方向走（统一向左或向右）

直到找到空位置，插入新节点。

	bool Insert(const K& key){if (_root == nullptr){_root = new node(key);return true;}//树为空，直接创建新节点作为根节点node* cur = _root;  //树不为空，从根开始比较node* parent = nullptr;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}//插入值小于当前节点值 → 往左子树走else if (cur->_key < key){parent = cur;cur = cur->_right;}//插入值大于当前节点值 → 往右子树走else  return false;//这里实现不支持插入的}//直到走空停下来，插入新节点cur = new node(key);if (parent->_key > key){parent->_left = cur;}else{parent->_right = cur;}return true;}

为什么增加parent指针？

保证在插入新节点时，能找到其父节点并正确连接。 parent->_key > key；这一步判断左右孩子，parent->_left = cur; 这一步进行链接。所以下面只要有链接需要，都要增加parent指针。

2.⼆叉搜索树的查找

查找过程与插入类似，也是“比大小，定方向”：

从根开始比较：

查找值大于当前节点值 → 往右子树找

查找值小于当前节点值 → 往左子树找

查找值等于当前节点值 → 找到目标

最多查找树的高度次，如果走到空还没找到，说明该值不存在。

注意：如果支持重复值，通常要求找到中序遍历的第一个匹配值。

//不支持重复值
bool Find(const K& key)
{node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else  return true;}return false;
}

怎么查找中序遍历的第一个重复值

中序遍历是“左根右”，找到相等的不要停，再往左树走找相等的，直到左树为空，就是中序遍历的第一个重复值。

Node* Find(const K& key) {Node* cur = _root;Node* firstFound = nullptr; // 记录第一个找到的节点while (cur) {if (cur->_key < key) cur = cur->_right;else if (cur->_key > key) cur = cur->_left;else {// 找到匹配的节点，但可能不是中序的第一个// 继续往左走，尝试找到更早出现的相同值firstFound = cur; // 记录当前找到的cur = cur->_left; // 继续向左寻找}}return firstFound; // 返回找到的第一个节点（可能为nullptr）
}

3. ⼆叉搜索树的删除

这个就有一些难度了，我认为难点只有两个，一个是删完这个结点仍然要保持规则，一个是删完之后要重新链接其附近的结点。因为我们链接时只用看该结点的左右孩子，那么我们就可以分为四类。

（1）删除叶子结点N（左右孩子都为空）

这可太好了，直接删除就好了，不会影响其他结点。

（2）删除只有右孩子的结点N

把N结点的⽗亲对应的孩⼦指针指向N的右孩⼦，直接删除N结点。比如N结点是其父亲的左结点，那么就把父亲的左结点指向N的右孩⼦，再删除N，由于N结点是其父亲的左结点，所以以N为根的树的所有结点都小于N的父亲，不会影响规则。

（3）删除只有左孩子的结点N

与上面类似，将N结点的父节点的对应指针指向该节点的左孩子。

我们看这三种情况，都是先判断N结点是其父亲的什么结点，然后把N结点不空的那一个孩子赋给N结点对应其父亲的结点，要是都为空，那就随便赋呗，反正是空，最后删除就行。所以可以写成一种。

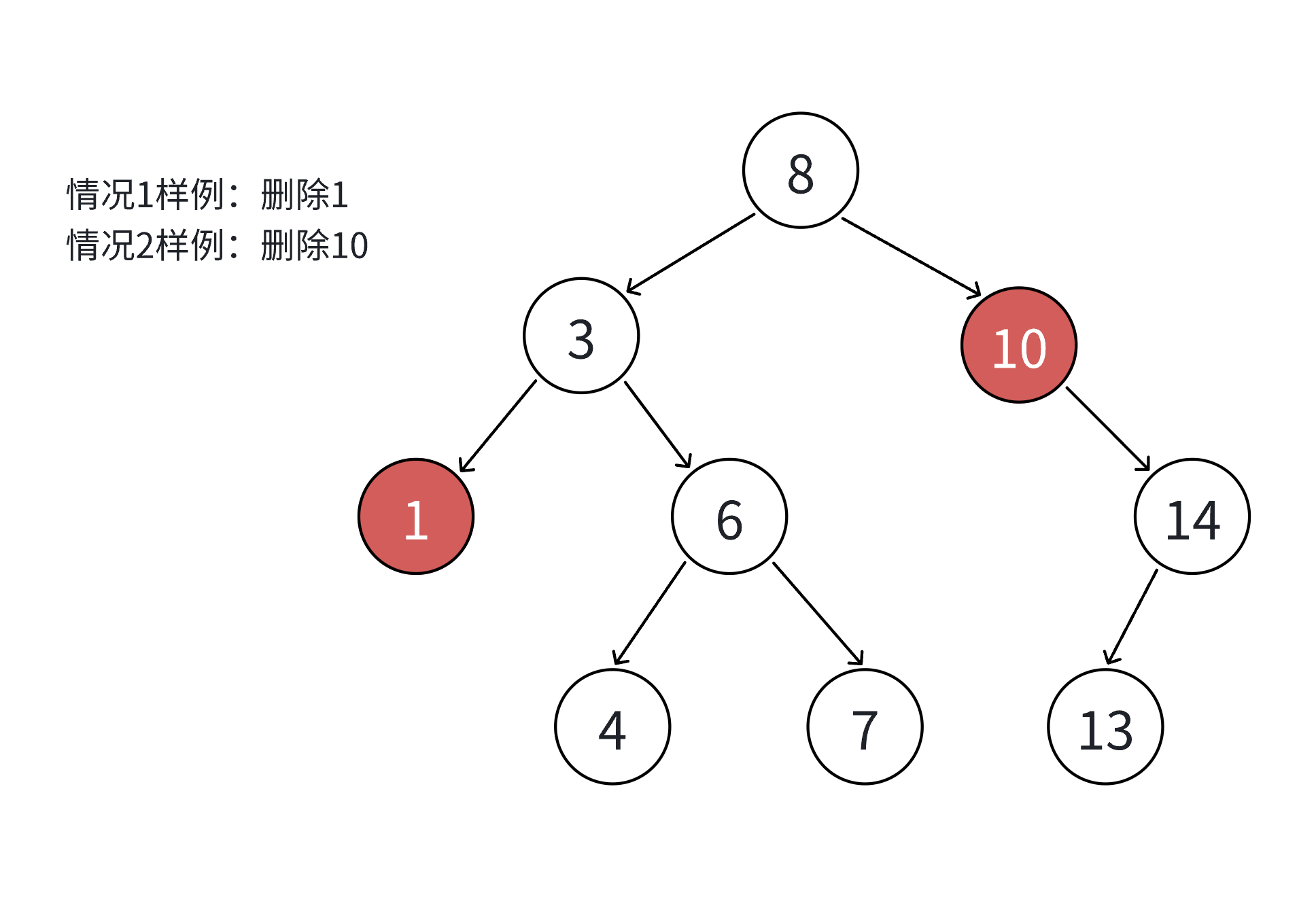
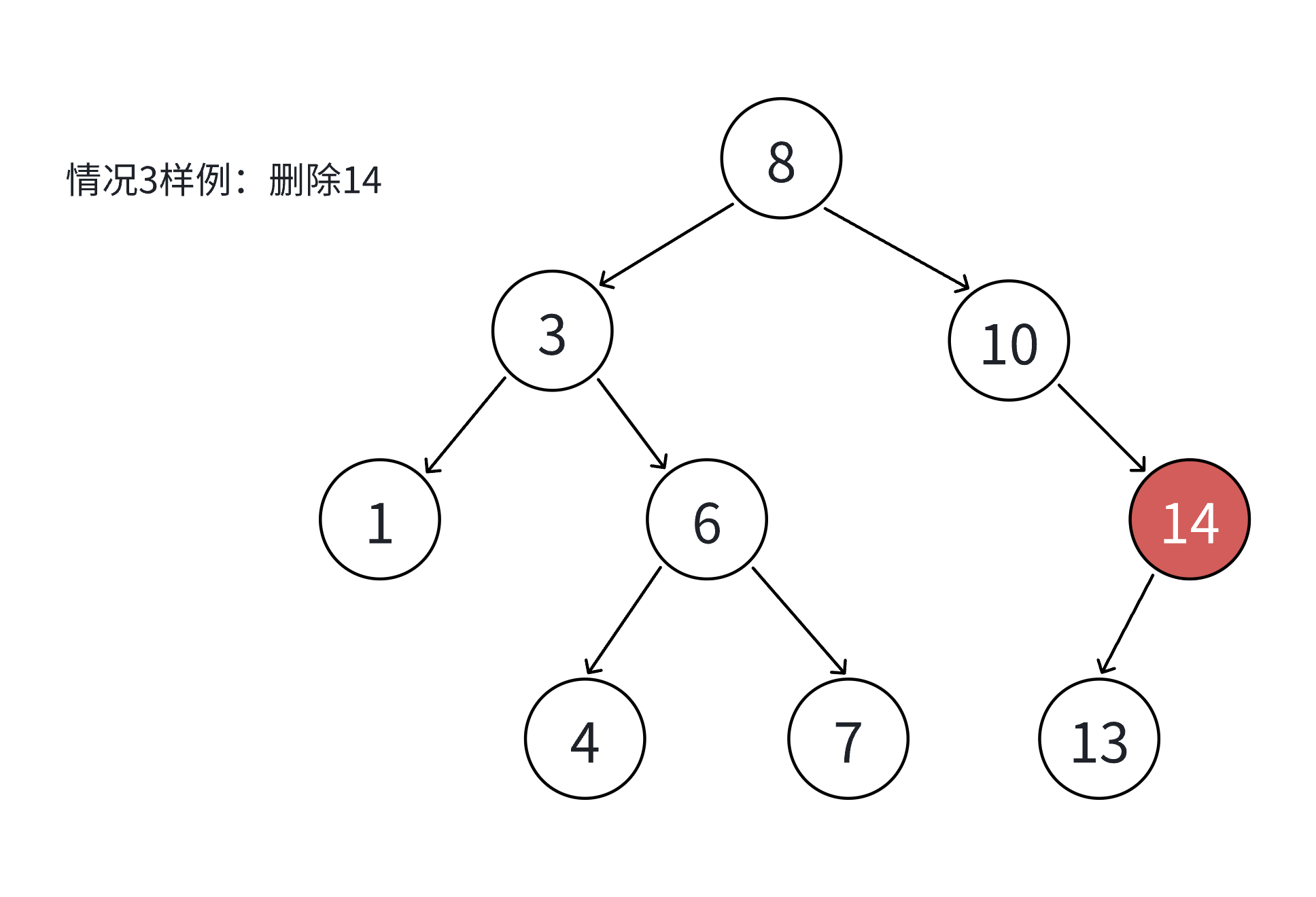
if (cur->_left == nullptr)
{if (parent == nullptr)_root = cur->_right;//防止删根else if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;delete cur;return true;
}
else if (cur->_right == nullptr)
{if (parent == nullptr)_root = cur->_left;else if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;delete cur;return true;
}
else
{ //......
}

（4）删除有两个孩子的结点N

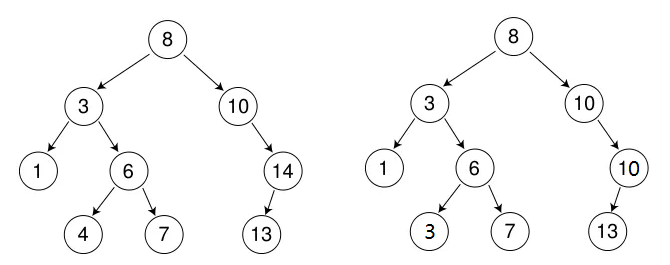
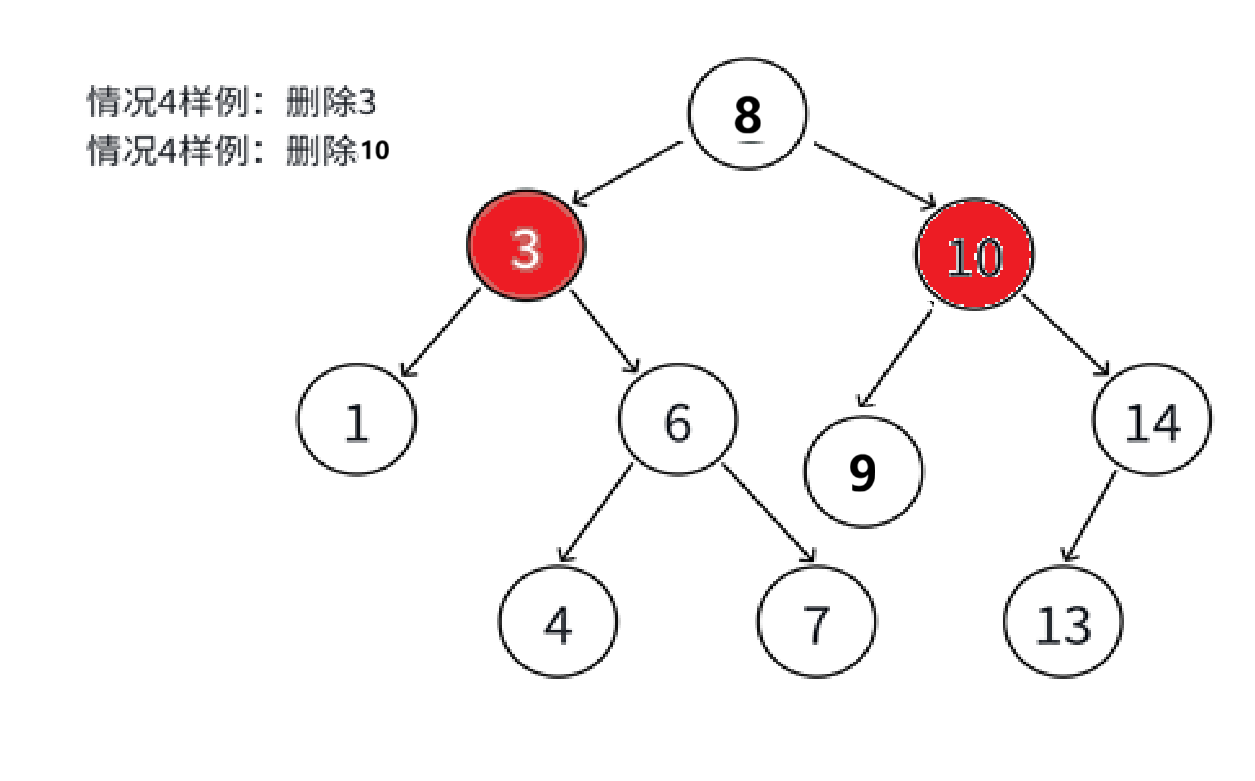
这时候我们直接删除就无法链接了，所以要用替换法。那用哪个结点替换后可以符合规则呢？答案是结点N的左子树的最右结点或右子树的最左结点。

如果用其左子树的最右结点，那么就可以保证，我比N的所有左结点都大，而又因为我在N的左子树，我又比N的所有右结点都小，而且我不可能破坏我与我父亲的关系，因为我是在N的子树里的结点。如果用其右子树的最左结点，也是一样。

替换后如何链接

以用其左子树的最右结点替换为例，我们直接把值赋给要删除的结点cur即可，cur的链接关系不用变。我们最后是要删除拿来替换的结点，而它一定是没有右结点，又返回到上面的情况了。要注意cur的左结点就没有右结点的情况，要单独考虑（比如下面删除10）

node* lmaxnp = cur;
node* lmaxn = cur->_left;
while (lmaxn->_right)
{lmaxnp = lmaxn;lmaxn = lmaxn->_right;
}
//找到左子树的最右结点
cur->_key = lmaxn->_key;
//替换if (lmaxnp->_left == lmaxn)
lmaxnp->_left = lmaxn->_left;
else
lmaxnp->_right = lmaxn->_left;
//这么写是为了防止cur->_left就是要找的最大值delete lmaxn;

完整代码：


template<class T>
struct BTNode
{T _key;BTNode<T>* _left;BTNode<T>* _right;BTNode(const T& key):_key(key), _left(nullptr), _right(nullptr){}
};template<class K>
class BSTree
{
private:typedef BTNode<K> node;node* _root = nullptr;void _InOrder(node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}public:BSTree() = default;bool Insert(const K& key){if (_root == nullptr){_root = new node(key);return true;}node* cur = _root;node* parent = nullptr;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else  return false;}cur = new node(key);if (parent->_key > key){parent->_left = cur;}else{parent->_right = cur;}return true;}bool Find(const K& key){node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else  return true;}return false;}bool Erase(const K& key){node* cur = _root;node* parent = nullptr;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{if (cur->_left == nullptr){if (parent == nullptr)_root = cur->_right;//防止删根else if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;delete cur;return true;}else if (cur->_right == nullptr){if (parent == nullptr)_root = cur->_left;else if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;delete cur;return true;}else{node* lmaxnp = cur;node* lmaxn = cur->_left;while (lmaxn->_right){lmaxnp = lmaxn;lmaxn = lmaxn->_right;}cur->_key = lmaxn->_key;if (lmaxnp->_left == lmaxn)lmaxnp->_left = lmaxn->_left;elselmaxnp->_right = lmaxn->_left;//这么写是为了防止cur->_left就是要找的最大值delete lmaxn;return true;}}}return 0;}//中序输出后，数据可以从小到大排列void InOrder(){_InOrder(_root);cout << endl;}};

三、二叉搜索树的应用模型

1. Key模型（纯关键词搜索）

结构中只存储key，用于判断某个值是否存在：

场景1：小区车牌识别系统 - 判断车牌是否在授权列表中
场景2：单词拼写检查 - 判断单词是否在词典中

2. Key/Value模型（关键词与对应值）

每个key对应一个value，用于通过key查找对应的value：

场景1：中英词典 - 通过英文单词查找中文释义
场景2：停车场计费系统 - 通过车牌查找入场时间，计算停车费用

场景3：单词频率统计 - 统计每个单词在文章中出现的次数

Key/Value模型的二叉搜索树实现与Key模型类似，只是在节点中增加了value成员，插入和查找时以key为依据，但可以访问和修改对应的value。

下面我实现一个Key/Value模型的二叉搜索树，这主要用到我们泛型编程的思想

（这只是开始，后面几篇容器的封装才真正考验你泛型编程的功底！）

#include <iostream>
#include <string>
using namespace std;template<class K, class V>
struct BSTNode {K _key;V _value;BSTNode<K, V>* _left;BSTNode<K, V>* _right;BSTNode(const K& key, const V& value): _key(key), _value(value), _left(nullptr), _right(nullptr) {}
};//支持重复键
template<class K, class V>
class BSTree {typedef BSTNode<K, V> Node;
public:bool Insert(const K& key, const V& value) {if (_root == nullptr) {_root = new Node(key, value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur) {parent = cur;if (cur->_key < key) {cur = cur->_right;} else if (cur->_key > key) {cur = cur->_left;} else {// 键已存在，根据需求处理：// 1. 返回false表示插入失败// 2. 更新值cur->_value = value;return true;}}cur = new Node(key, value);if (parent->_key < key) {parent->_right = cur;} else {parent->_left = cur;}return true;}Node* Find(const K& key) {Node* cur = _root;Node* firstFound = nullptr;while (cur) {if (cur->_key < key) {cur = cur->_right;} else if (cur->_key > key) {cur = cur->_left;} else {// 找到匹配节点，记录并继续向左寻找更早的匹配firstFound = cur;cur = cur->_left;}}return firstFound;}bool Erase(const K& key) {Node* parent = nullptr;Node* cur = _root;while (cur) {if (cur->_key < key) {parent = cur;cur = cur->_right;} else if (cur->_key > key) {parent = cur;cur = cur->_left;} else {if (cur->_left == nullptr) {if (parent == nullptr) {_root = cur->_right;} else {if (parent->_left == cur) parent->_left = cur->_right;else parent->_right = cur->_right;}delete cur;} else if (cur->_right == nullptr) {if (parent == nullptr) {_root = cur->_left;} else {if (parent->_left == cur) parent->_left = cur->_left;else parent->_right = cur->_left;}delete cur;} else {Node* rightMinParent = cur;Node* rightMin = cur->_right;while (rightMin->_left) {rightMinParent = rightMin;rightMin = rightMin->_left;}cur->_key = rightMin->_key;cur->_value = rightMin->_value;if (rightMinParent->_left == rightMin)rightMinParent->_left = rightMin->_right;elserightMinParent->_right = rightMin->_right;delete rightMin;}return true;}}return false;}void InOrder() {_InOrder(_root);cout << endl;}// 统计某个键出现的次数int Count(const K& key) {return _Count(_root, key);}private:void _InOrder(Node* root) {if (root == nullptr) return;_InOrder(root->_left);cout << root->_key << ":" << root->_value << " ";_InOrder(root->_right);}//递归思想int _Count(Node* root, const K& key) {if (root == nullptr) return 0;int count = 0;if (root->_key == key) {count = 1;}// 由于可能有重复键，需要搜索左右子树return count + _Count(root->_left, key) + _Count(root->_right, key);}Node* _root = nullptr;
};

四、二叉搜索树的性能分析

二叉搜索树的性能高度依赖于树的形状：

最优情况：树为完全二叉树（或接近完全二叉树），高度为 log₂N，此时增删查改的时间复杂度为 O(logN)
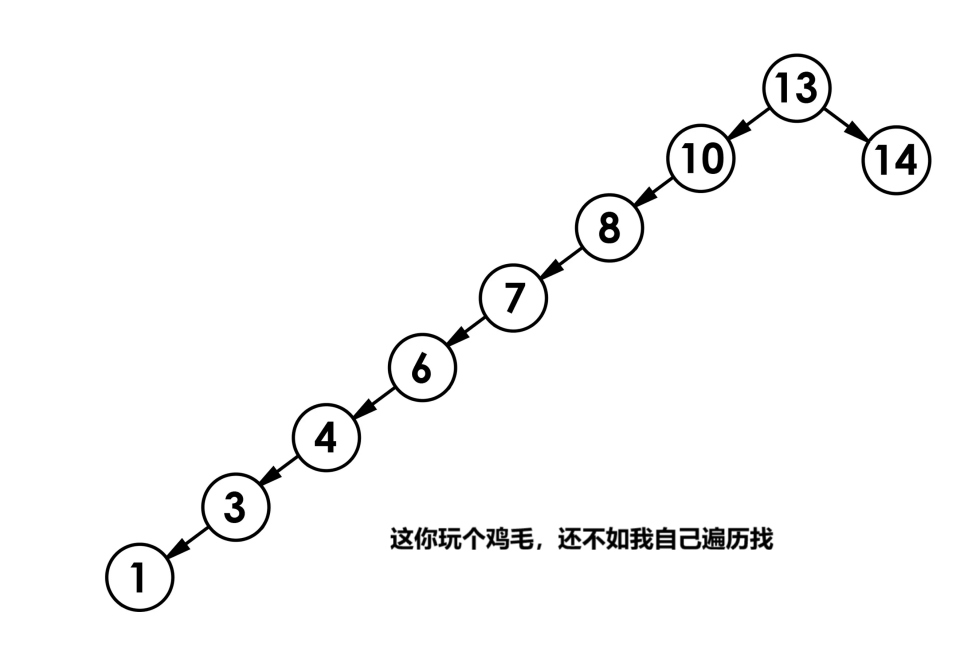
最差情况：树退化为单支树（类似链表），高度为 N，此时时间复杂度退化为 O(N)

正因为存在退化为O(N)的风险，单纯的二叉搜索树无法满足实际需求，这才催生了AVL树和红黑树等平衡二叉搜索树。我们下节讲。

与二分查找的对比
有人可能会问：二分查找也有O(logN)的查找效率，为什么还需要二叉搜索树？
二分查找有两大局限：

需要数据存储在支持随机访问的结构中（如数组），且必须有序

插入和删除数据效率很低，需要移动大量元素

而二叉搜索树在保持较好查找效率的同时，也提供了高效的插入和删除能力。

五、二叉树进阶算法题

（点击名称即可跳转到对应OJ题）

下面问题统一的树的结构：

struct TreeNode 
{int val;TreeNode* left;TreeNode* right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};

1. 根据二叉树创建字符串

问题核心：分析加括号的时机，只有一个结点有左树无右树时，才可以不加右树的括号

关键步骤：前序递归

根节点：直接输出节点值。

左子树：左子树不管是否为空，必须加括号，除非两个子树全是空。

右子树：右子树存在，就给右子树加括号；不存在就不加。

string tree2str(TreeNode* root) 
{string res;if (root == nullptr) return res;//访问跟res += to_string(root->val);//遍历左树（当左树空，右树不空时只用于打括号）if (root->left || root->right){res += '(';res += tree2str(root->left);res += ')';}//遍历右树if (root->right){res += '(';res += tree2str(root->right);res += ')';}return res;
}

2. 正向层序遍历

之前讲过层序遍历了，不同点是这个需要用动态二维数组存储，所以要加一个size记录每一层结点的数量，确保上一层出完队列后，它带入且仅带入了下一层的全部结点。

vector<vector<int>> levelOrder(TreeNode* root) 
{vector<vector<int>> vv;queue<TreeNode*> q;if (root){q.push(root);}while (!q.empty()){size_t size = q.size();vector<int> v;while (size--){if (q.front()->left)q.push(q.front()->left);if (q.front()->right)q.push(q.front()->right);v.push_back(q.front()->val);q.pop();}vv.push_back(v);}return vv;
}

3. 反向层序遍历

结尾把数组倒置就行

vector<vector<int>> levelOrder(TreeNode* root)
{vector<vector<int>> vv;queue<TreeNode*> q;if (root){q.push(root);}while (!q.empty()){size_t size = q.size();vector<int> v;while (size--){if (q.front()->left)q.push(q.front()->left);if (q.front()->right)q.push(q.front()->right);v.push_back(q.front()->val);q.pop();}vv.push_back(v);}reverse(vv.begin(), vv.end());return vv;
}

4. 最近公共祖先

关键点：两个结点一定分别分布在最近公共祖先的左右两棵子树中，或者其中一个就是最近公共祖先！搞清楚这个问题其实就解决了。

方法一：依次找每个有用结点（要是都在左边，右子树就不用找了）的左右子树，直到成功在两个子树中找到。

方法二：用栈记录根节点到p、q的路径，找最后一个公共节点

// //最近公共祖先
//方法一
bool Seeknode(TreeNode* root, TreeNode* p)
{if (!root) return false;if (root == p) return true;bool a = Seeknode(root->left, p);if (a) return true;bool b = Seeknode(root->right, p);return b;
}TreeNode* lowestCommonAncestor1(TreeNode* root, TreeNode* p, TreeNode* q) 
{if (root == p || root == q){return root;}bool pInLeft, pInRight, qInLeft, qInRight;//注意题目中说一定存在pInLeft = Seeknode(root->left, p);pInRight = !pInLeft;  //减少递归的重要步骤qInLeft = Seeknode(root->left, q);qInRight = !qInLeft;  //减少递归的重要步骤if ((pInLeft && qInRight) || (qInLeft && pInRight)){return root;}else if (pInLeft && qInLeft){return lowestCommonAncestor1(root->left, p, q);}else{return lowestCommonAncestor1(root->right, p, q);}}//方法二
bool NodePath(TreeNode* root, TreeNode* p, stack<TreeNode*>& st)
{if (!root) return false;st.push(root);if (root == p)  return true;if (NodePath(root->left, p, st))  return true;if (NodePath(root->right, p, st))  return true;st.pop();return false;
}
//递归找路径（难点）TreeNode* GetIntersection(stack<TreeNode*> st1, stack<TreeNode*> st2)
{if (st1.size() > st2.size()){while (st1.size() != st2.size()){st1.pop();}}else if (st1.size() < st2.size()){while (st1.size() != st2.size()){st2.pop();}}while (st1.top() != st2.top()){st1.pop();st2.pop();}return st1.top();
}
TreeNode* lowestCommonAncestor2(TreeNode* root, TreeNode* p, TreeNode* q)
{stack<TreeNode*> st1;stack<TreeNode*> st2;NodePath(root, p, st1);NodePath(root, q, st2);TreeNode* res = GetIntersection(st1, st2);return res;
}

5. 从前序/后序与中序遍历序列构造二叉树

核心思想：利用前序确定根节点，利用中序划分左右子树，递归构建

关键步骤：

确定根节点：前序遍历的第一个元素就是当前子树的根

定位中序位置：在中序遍历中找到根节点位置，左边是左子树，右边是右子树

递归构建：

左子树：前序下一元素 + 中序左半部分

右子树：前序后续元素 + 中序右半部分

//从前序与中序遍历序列构造二叉树
TreeNode* _buildTree1
(vector<int>& preorder, vector<int>& inorder, int& prei, int inbegin, int inend)
{if (inbegin > inend)  return nullptr;TreeNode* root = new TreeNode;int temp = preorder[prei];prei++;root->val = temp;int rootIndex;for (rootIndex = inbegin; rootIndex <= inend; rootIndex++){if (temp == inorder[rootIndex])  break;}root->left = _buildTree1(preorder, inorder, prei, inbegin, rootIndex - 1);root->right = _buildTree1(preorder, inorder, prei, rootIndex + 1, inend);return root;
}
TreeNode* buildTree1(vector<int>& preorder, vector<int>& inorder) 
{int i = 0;TreeNode * res = _buildTree1(preorder, inorder, i, 0, inorder.size() - 1);return res;
}

后序也是一样，左右根，就是倒着来，先确立根，在确定右子树，然后左子树。

6. 非递归前序遍历/中序遍历

        其实就是用循环和栈模拟递归，因为递归不就是不断地压栈再出栈吗？
        把结点存在栈中，方便类似递归回退时取父路径结点。跟这里不同的是，这里把一棵二叉树分为两个部分：先访问左路结点，再访问左路结点的右子树。
        这里访问右子树要以循环，从栈依次取出这些结点，循环子问题的思想访问左路结点的右子树。

//非递归前序遍历
vector<int> preorderTraversal(TreeNode* root) 
{vector<int> v;stack<TreeNode*> st;if (!root) return v;TreeNode* cur = root;while (cur || !st.empty()){//访问左路结点，左路结点入栈while (cur){v.push_back(cur->val);st.push(cur);cur = cur->left;}if (!st.empty()){//从栈中依次访问左路结点的右子树cur = st.top();st.pop();//循环子问题方式访问左路结点的右子树cur = cur->right;}}return v;
}

//非递归中序遍历
vector<int> inorderTraversal(TreeNode* root)
{vector<int> v;stack<TreeNode*> st;if (!root) return v;TreeNode* cur = root;while (cur || !st.empty()){while (cur){st.push(cur);cur = cur->left;}if (!st.empty()){cur = st.top();st.pop();v.push_back(cur->val);//只是访问时机发生变化cur = cur->right;}}return v;
}

7. 非递归后序遍历

可以按上面的思路做，但是有一个难点是，由于后序遍历的顺序是左子树 → 右子树 → 根，所以当取到左路节点的右子树时，我们不知道它是否访问过了。例如下图：

我们栈顶是2时，有可能是访问6之后，回到2，发现还有右子树继续访问7；也可能是访问7之后回到2来访问根。所以我们需要做标记，我认为这个方法操作难度其实挺大的，我先放这种解法，之后我会再讲一种简单的。

vector<int> postorderTraversal(TreeNode* root) {TreeNode* cur = root;stack<TreeNode*> s;vector<int> v;TreeNode* prev = nullptr;while (cur || !s.empty()){//访问一颗树的开始while (cur){s.push(cur);cur = cur->left;}TreeNode* top = s.top();// top结点的右为空 或者 上一个访问结点等于他的右孩子// 那么说明(空)不用访问 或者 (不为空)右子树已经访问过了// 那么说明当前结点左右子树都访问过了，可以访问当前结点了if (top->right == nullptr || top->right == prev){s.pop();v.push_back(top->val);prev = top;}else{// 右子树不为空，且没有访问，循环子问题方式右子树cur = top->right;}}return v;
}

方法二：

出现以上问题的本质是我的根在最后访问，而我要访问左右子树又必须经过根。那如果我倒着来，变成右左根，再把数组倒置，不是也可以吗？如果我能保证我每棵子树都可以先访问根，再将他的左子树压入栈，之后再将右子树压入栈（后进先出），那就保证了右左根。所以代码如下：
//非递归后序遍历
vector<int> postorderTraversal(TreeNode* root)
{//根右左vector<int> v;stack<TreeNode*> st;if (!root) return v;st.push(root);while (!st.empty()){TreeNode* temp = st.top();st.pop();v.push_back(temp->val);if (temp->left) st.push(temp->left);if (temp->right) st.push(temp->right);//它的右子树在栈顶，而每次离开时又会带入它的左右子树，//所以当它的右子树没有走完时，它不可能走到左树}reverse(v.begin(), v.end());return v;
}

8. 将二叉搜索树转化为排序的双向链表

中序遍历二叉搜索树时，遍历顺序本身就是有序的。

思路：

使用两个指针：cur表示当前中序遍历到的节点，prev表示上一个中序遍历的节点

当遍历到cur节点时，将cur->left指向prev，建立指向前驱的链接

此时cur->right无法指向中序下一个节点，因为还不知道下一个节点是谁

但是可以通过prev->right指向cur，为上一个节点建立指向后继的链接

即：

每个节点的左指针在遍历到该节点时修改，指向前驱节点

每个节点的右指针在遍历到下一个节点时，通过前一个节点的prev->right = cur来修改，指向后继节点

//将二叉搜索树转化为排序的双向链表
void InOrderConvert(Node* cur, Node*& prev)
{if (cur == nullptr)return;InOrderConvert(cur->left, prev);cur->left = prev;if (prev)  prev->right = cur;prev = cur;InOrderConvert(cur->right, prev);
}Node* treeToDoublyList(Node* root) 
{if (root == nullptr)return nullptr;Node* prev = nullptr;InOrderConvert(root, prev);Node* head = root;while (head->left){head = head->left;}head->left = prev;prev->right = head;return head;
}

后记：这几道算法题是非常重要的，大家一定要重点掌握。后面学习AVL与红黑树会难一些，但也是面试的高频考点，如果有帮助大家可以点个红心支持一下。