数据集预处理：规范化和标准化

一、说明

训练监督式机器学习模型包括将训练数据集中的数据输入模型，模型生成预测结果。这些预测结果随后与真实值（即训练数据对应的预期目标）进行比较。然后通过最小化代价函数、误差函数或损失函数来优化模型。

在将数据集输入模型之前，准备数据集非常重要。如果在未进行数据准备的情况下直接输入数据，模型可能会表现出一些非常奇怪的行为——而且训练过程可能会变得非常困难，甚至无法进行。在这些情况下，检查模型代码可能会发现你忘记应用归一化或标准化。它们是什么？为什么需要它们？它们是如何工作的？本文将详细探讨这些问题。

首先，我们将探讨为什么需要归一化或标准化数据集。接下来，我们将了解这些技术的实际应用。最后，我们将提供大量使用 Scikit-learn 和 Python 的分步示例，指导您如何为机器学习模型准备数据集。

二、特征缩放的归一化和标准化

在探讨具体内容之前，我认为我们应该首先理解其背后的原因。至少，它解释了为什么需要使用特定的技术或方法。归一化和标准化也是如此。它们为什么必要？让我们更深入地探讨这个问题。

2.1 机器学习算法必需标准化和归一化

训练监督式机器学习模型时，你需要向模型输入数据，进行预测，然后不断改进模型。正如引言中所述，这是通过最小化成本/误差/损失函数来实现的，从而使我们能够以新颖的方式改进模型。

例如，支持向量机通过识别两类之间间隔最大的支持向量进行优化，从而计算距离度量。神经网络则使用梯度下降法进行优化，即沿着损失函数下降最快的方向向下移动。还有许多其他方法。以下是一些关于为什么机器学习算法需要对数据集进行缩放的见解（维基百科，2011）。

• 随着数据集规模的扩大，梯度下降法的收敛速度会大大加快。
• 如果模型依赖于距离度量（例如，支持向量机），则在数据集缩放后，距离仍然具有可比性。事实上，如果不进行缩放，当某个特征相对于其他特征而言规模巨大时，损失的计算可能会“受该特定特征的影响”（维基百科，2011）。
• 如果应用正则化，则必须同时应用缩放；否则，某些特征可能会受到不必要的过度惩罚。

2.2 标准化和归一化有助于特征选择。

如果给我们一个跑步者日记的数据集，而我们的目标是学习一些变量与跑步者表现之间的预测模型，我们通常会执行特征选择程序，因为我们不能简单地输入所有样本，原因有二：

• 1—— 维度灾难：如果我们把数据集看作一个特征空间，每个特征（即列）代表一个维度，那么如果我们使用很多特征，这个空间就会变成多维的。维度越多，所需的训练数据就越多；这种需求呈指数级增长。因此，虽然我们应该使用足够的特征，但我们并不想使用每一个特征。
• 2 ——我们不希望采用贡献较小的特征。有些特征（列）对输出的贡献比其他特征小。即使剔除这些特征，模型可能仍然有效，但计算成本会大幅降低。因此，我们希望能够选择影响最大的特征。
  在机器学习问题中，如果要在高维特征空间中从有限数量的数据样本中学习“自然状态”，并且每个特征都有一系列可能的值，通常需要大量的训练数据来确保每种值组合都有多个样本。——维基百科（无日期）关于维度诅咒

请记住以上内容，我们接下来将查看以下数据集：

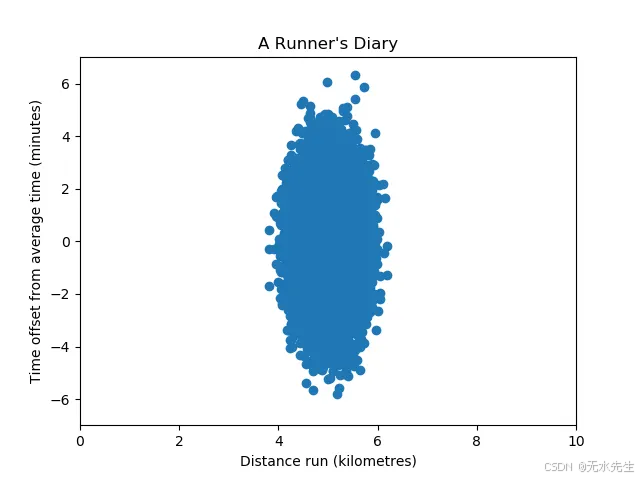
这里，时间偏移变量的方差大于距离运行变量的方差。

因此， PCA自然会选择时间偏移变量而不是距离运行变量，因为那里的特征对更为显著。

然而，这并不一定意味着它实际上更重要——我们不能直接比较方差。只有当方差可比，即它们所代表的单位尺度相等时，我们才能放心地使用像PCA这样的算法进行特征选择。这就是为什么我们必须找到一种方法来使我们的变量具有可比性。

2.3 引入特征缩放

更广泛地说，特征缩放贯穿于整个数据准备阶段。

特征缩放是一种用于规范化数据中自变量或特征范围的方法。在数据处理中，它也被称为数据归一化，通常在数据预处理步骤中执行。_ 维基百科（2011）

特征缩放有两种基本方法，我们将在本文的其余部分进行讨论：

• 重新缩放，或最小-最大归一化：我们将数据缩放到以下两个范围之一：[0, 1] 或 [a, b]，通常是 [-1, 1]。
• 标准化，或Z 分数归一化：我们将数据缩放，使均值为零，方差为 1。
  让我们仔细看看这三种方法，它们是如何运作的，以及它们在什么情况下最有效。

三、重新缩放（最小-最大归一化）

重新缩放，或称最小-最大归一化，是一种将数据转换为两个范围之一（[0, 1] 或 [a, b]）的简单方法。它主要依赖于数据集中的最小值和最大值来进行数据归一化。

3.1 工作原理——[0,1] 方式

假设我们有以下数组：

数据集 = np.array([ 1.0 , 12.4 , 3.9 , 10.4 ])
最小-最大归一化在 [0, 1] 范围内可以定义如下：

标准化数据集 = (数据集 -最小值(数据集)) / (最大值(数据集) -最小值(数据集))
因此，我们可以用一种简单的方法，使用 NumPy，将数据归一化到 [0, 1] 范围内，具体方法如下：

import numpy as np 
dataset = np.array([ 1.0 , 12.4 , 3.9 , 10.4 ]) 
normalized_dataset = (dataset - np. min ( dataset)) / (np. max (dataset) - np. min (dataset)) 
print (normalized_dataset)

这确实会生成一个数组，其中最小值为 0.0，最大值为 1.0：

[0. 1. 0.25438596 0.8245614 ]

3.2 工作原理——[a,b] 方法

如果我们想将其缩放到其他任意范围（例如 [0, 1.5]），我们可以应用最小-最大归一化，但范围是 [a, b]，您可以自己选择 a 和 b。

我们可以使用以下公式进行归一化：

标准化数据集 = a + ((数据集 -最小值(数据集)) * (b - a) / (最大值(数据集) -最小值(数据集)))
或者，对于上一节中的数据集，使用一个简单的 Python 实现：

import numpy as np 
a = 0b = 1.5dataset = np.array([ 1.0 , 12.4 , 3.9 , 10.4 ]) 
normalized_dataset = a + ((dataset - np. min (dataset)) * (b - a) / (np. max (dataset) - np. min (dataset))) 
print (normalized_dataset)

由此得出：

[0. 1.5 0.38157895 1.23684211]

3.3 应用 Scikit-learn 中的 MinMaxScaler

Scikit-learn 是一个广泛使用的机器学习库，用于训练各种传统的机器学习算法，它包含一个名为 MinMaxScaler 的组件，该组件是 sklearn.preprocessing API 的一部分。

它允许我们对数据集应用指定范围的缩放器，然后对数据进行转换。以下代码演示了如何实现它。

import numpy as np 
from sklearn.preprocessing import MinMaxScaler 
dataset = np.array([ 1.0 , 12.4 , 3.9 , 10.4 ]).reshape(- 1 , 1 ) 
scaler = MinMaxScaler(feature_range=( 0 , 1.5 )) 
scaler.fit(dataset) 
normalized_dataset = scaler.transform(dataset) 
print (normalized_dataset)

我们numpy整体进口，并且MinMaxScaler来自sklearn.preprocessing.
我们定义了之前定义的 NumPy 数组，但现在需要对其进行重塑。reshape(-1, 1)这是 Scikit-learn 对每个数组元素只有一个特征的数组的要求（在我们的例子中，由于我们使用的是标量值，所以符合这个条件）。
然后我们初始化MinMaxScaler，并在这里指定我们的 [a, b] 范围：feature_range=(0, 1.5)。当然，由于 [0, 1] 也是一个 [a, b] 范围，我们也可以使用⁣ MinMaxScaler来实现它。
然后我们使用缩放器将数据拟合到缩放器中scaler.fit(dataset)。这样，它就能够转换数据集了。
最后，我们dataset使用⁣进行转换scaler.transform(dataset)并打印结果。
打印出来后，我们可以看到结果与我们用简单方法得到的结果相同：

[[ 0. ]
[ 1.5 ]
[ 0.38157895 ]
[ 1.23684211 ]]

四、标准化（Z 尺度归一化）

在前面的例子中，我们根据最小值和最大值调整了数据集。而均值和标准差则没有标准化，这意味着均值等于零，标准差等于一。

print (normalized_dataset) 
print (np.mean(normalized_dataset)) 
print (np.std(normalized_dataset))
[[0. ] 
[1.5 ] 
[0.38157895] 
[1.23684211]] 
0.7796052631578947 
0.611196249385709

由于我们的归一化方法的局限性不同，因此将结果与PCA等方法进行比较仍然是（某种程度上）不公平的。

例如，如果我们使用不同的数据集，结果就会有所不同：

import numpy as np 
from sklearn.preprocessing import MinMaxScaler 
dataset = np.array([ 2.4 , 6.2 , 1.8 , 9.0 ]).reshape(- 1 , 1 ) 
scaler = MinMaxScaler(feature_range=( 0 , 1.5 )) 
scaler.fit(dataset) 
normalized_dataset = scaler.transform(dataset) 
print (normalized_dataset) 
print (np.mean(normalized_dataset)) 
print (np.std(normalized_dataset)) 

[[ 0.125 ]
[ 0.91666667 ]
[ 0. ]
[ 1.5 ]]
0.6354166666666665
0.6105090942538584
这时，标准化过程（也称为Z 分数归一化）就显得尤为重要。我们不再依赖最小值和最大值，而是利用数据集的均值和标准差。这样一来，所有特征的均值都为零，方差为一，从而可以有效地比较不同特征之间的方差。

工作原理
标准化公式如下：

标准化数据集 = (数据集 - 平均值(数据集)) / 标准差(数据集)
换句话说，对于数据集中的每个实例，我们减去均值并除以标准差。通过从每个实例中减去均值，我们实际上是将这些实例向均值为 0 的方向移动（因为我们从所有实例中都减去了均值）。此外，通过除以标准差，我们创建了一个数据集，其中每个值都表示它们与均值之间的偏差程度（以标准差为单位）。

Python 示例
这也可以用Python实现：

import numpy as np 
dataset = np.array([ 1.0 , 2.0 , 3.0 , 3.0 , 3.0 , 2.0 , 1.0 ]) 
standardsed_dataset = (dataset - np.average(dataset)) / (np.std(dataset)) 
print (standardized_dataset)
由此得出：[-1.37198868 -0.17149859 1.02899151 1.02899151 1.02899151 -0.17149859 
-1.37198868]

在 Scikit-learn 中，该sklearn.preprocessing模块提供了⁣，StandardScaler它可以帮助我们以高效的方式执行相同的操作。

import numpy as np 
from sklearn.preprocessing import StandardScaler 
dataset = np.array([ 1.0 , 2.0 , 3.0 , 3.0 , 3.0 , 2.0 , 1.0 ]).reshape(- 1 , 1 ) 
scaler = StandardScaler() 
scaler.fit(dataset) 
standardsed_dataset = scaler.transform(dataset) 
print (standardized_dataset) 
print (np.mean(standardized_dataset)) 
print (np.std(standardized_dataset))
结果如下：[[-1.37198868] 
[-0.17149859] [ 
1.02899151 ] [ 1.02899151] [ 1.02899151] [-0.17149859] [-1.37198868]] 3.172065784643304e-17 1.0

我们看到均值非常接近 0 (3.17 x 10^{-17})，标准差为 1。

五、标准化与归一化：何时使用哪种方法

人们经常会问，何时应该使用归一化，何时应该使用标准化。这是一个很合理的问题，我自己也遇到过这种情况。

一般来说，一个好的指导原则是，当你想要对数据进行归一化，同时保持尺度上的某些差异时（因为单位保持不同），应用最小-最大归一化；当你想要使尺度具有可比性时（通过使用标准差），则利用标准化。

以下示例展示了标准化的影响。我们生成高斯数据，将其中一个轴拉长一定值，使两个轴难以直接比较，然后绘制图表来可视化数据。这样可以清晰地看到数据点的绝对值。接下来，应用标准化后，我们再次绘制数据图。此时，我们观察到均值已移至 (0, 0)，并且两个轴的方差也变得更加接近！

如果我们没有在这里应用特征缩放，像PCA这样的算法几乎肯定会骗过我们。

# 导入
import matplotlib.pyplot as plt 
from sklearn.datasets import make_gaussian_quantiles 
from sklearn.preprocessing import StandardScaler # 生成高斯数据
plt.title( "高斯数据，两类，均值在 (2,3)" ) 
X1, Y1 = make_gaussian_quantiles(n_features= 2 , n_classes= 2 , n_samples= 1000 , mean=( 2 , 3 )) # 拉伸其中一个坐标轴
X1[:, 1 ] = 2.63 * X1[:, 1 ] # 绘制数据
plt.scatter(X1[:, 0 ], X1[:, 1 ], marker= 'o' , c=Y1, s= 25 , edgecolor= 'k' ) 
axes = plt.gca() 
axes.set_xlim([- 5 , 20 ]) 
axes.set_ylim([- 5 , 20 ]) 
plt.show() # 标准化高斯数据
scaler = StandardScaler() 
scaler.fit(X1) 
X1 = scaler.transform(X1) # 绘制标准化数据
plt.title( "标准化后的高斯数据，两类，均值位于 (0,0)" ) 
plt.scatter(X1[:, 0 ], X1[:, 1 ], marker= 'o' , c=Y1, s= 25 , edgecolor= 'k' ) 
axes = plt.gca() 
axes.set_xlim([- 5 , 20 ]) 
axes.set_ylim([- 5 , 20 ]) 
plt.show()

六、总结

本文探讨了机器学习中的特征缩放问题。具体而言，我们研究了归一化（最小-最大归一化），它将数据集调整到 [a, b] 区间内。除了归一化之外，我们还讨论了标准化，它将尺度转换为标准差的倍数，从而使各轴在诸如主成分分析 (PCA) 等算法中具有可比性。我们通过逐步 Python 示例来说明我们的推理，其中包括一些使用标准 Scikit-learn 功能的示例。