第3节 RSA算法开启公钥加密时代
在1977年的麻省理工学院(MIT)计算机科学实验室,三位年轻而富有远见的学者——罗纳德·李维斯特(Ronald Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德尔曼(Leonard Adleman)——正夜以继日地解决一个困扰人类千年、在数字时代变得尤为紧迫的问题:如何在不泄露秘密的前提下,安全地分享秘密?
他们的研究成果,后来被命名为RSA算法(取自他们三人姓氏的首字母),不仅是人类历史上第一个实用的公钥加密算法,更是数字安全领域的一块基石,至今仍是支撑全球电子商务、安全通信和数字身份的核心技术。
1. 黎明前的迷雾:密钥分配的难题
在RSA诞生之前,所有的加密系统,无论是古老的凯撒密码,还是当时最先进的DES(数据加密标准,也于1977年发布),都属于对称加密的范畴。
对称加密系统的特点是:加密和解密使用同一把密钥。这就像一把双向锁。问题在于,如果你想与远在天边的朋友安全通信,你必须先通过一个完全安全(且难以实现)的渠道,将这把密钥秘密地交给对方。
在网络化通信的世界里,这被称为“密钥分配危机”。
1976年,Whitfield Diffie和马丁·赫尔曼Martin Hellman发表了具有里程碑意义的论文,提出了公钥密码学的颠覆性概念。
他们设想了一套非对称的密钥系统:每人拥有一个公钥(用于加密,可公开)和一个私钥(用于解密,必须保密)。这套系统被称为“单向陷门函数”:用公钥加密信息很容易,但没有私钥,几乎不可能解密。
然而,他们并没有提供一个实用、高效且安全的算法来实例化这个概念。
2. MIT三剑客:从理论到实践的飞跃
在MIT,罗纳德·李维斯特(Ronald Linn Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德尔曼(Leonard Adleman)接受了挑战。他们尝试了四十多种数学函数,但都未能找到一个既能安全加密、又能轻松解密的“陷门”。
直到有一天,李维斯特受到了一个数学问题的启发:大数的因数分解。
简单讲,如果一个数N是两个大质数p和q的乘积(即N = p * q),那么计算出N非常容易。但反过来,如果只知道N,想要找出p和q(即对N进行因数分解),在数学上是一个极其困难和耗时的问题,尤其当p和q是数百位长的质数时。
RSA三位学者意识到,这正是他们寻找的“单向陷门”:
单向性:从p, q计算N很容易(加密过程)。
陷门:只有知道p和q(即私钥),才能轻松解密。
经过进一步的数学推导,他们将这个因数分解的难题与数论中的欧拉函数和模幂运算结合起来,创造了今天我们所知的RSA算法。
1977年,他们正式发表了算法。RSA的诞生,一举解决了困扰数字通信的密钥分配难题,真正将公钥密码学从理论带入了实用的数字世界。
公钥密码也叫非对称密码,对比对称密码,非对称密码的加密密钥和解密密钥是不一样的。在非对称的加密算法中,分为公钥和私钥,其中公钥是公开的,私钥是所有者独自使用。公钥加密的数据可以使用私钥解密,私钥加密的数据可以使用公钥解密,因此这样可以节省所有参与加解密的人的存储密钥的压力,也可以解决密钥分配的问题。
3. 深度解析:RSA算法的技术心脏
RSA算法的安全性完全基于一个简单的数学难题:对极大整数进行因数分解的困难性。
它的核心机制在于利用一对密钥:公钥用于加密,私钥用于解密。
RSA的数学基础是:
欧拉定理/费马小定理的推广: 这是保证解密能够还原原始数据的理论依据。
大数因数分解的困难性: 这是保证算法安全的基石。
RSA算法的三个步骤
(1)密钥生成 (Key Generation)
这是最关键的一步,用于生成公钥和私钥:
步骤 I:选择质数
选择两个非常大且随机的质数p和q。这两个质数的长度通常在数百位(例如,1024位或2048位)。
步骤 II:计算模数N
计算N = p * q。
N将作为公钥和私钥的一部分,是公开的。
p和q必须严格保密。
步骤 III:计算欧拉函数
计算欧拉函数值,即小于N且与N互质的正整数的数量。对于质数p和q,计算公式为:
也必须严格保密。
步骤 IV:选择公钥指数e
选择一个整数e,作为公钥指数。$e$必须满足:
1 < e <
e与
互质(即它们的最大公约数为1)。
步骤 V:计算私钥指数d
计算一个整数d,作为私钥指数。d是e的模的乘法逆元。
简单来说,d必须满足等式:
这个d就是解密的“陷门”;它可以通过扩展欧几里得算法快速计算出来。
密钥对:
公钥 (Public Key, PK): (N, e)。可以公开发布。
私钥 (Private Key, SK): (N, d) 或 (p, q, d)。必须保密。
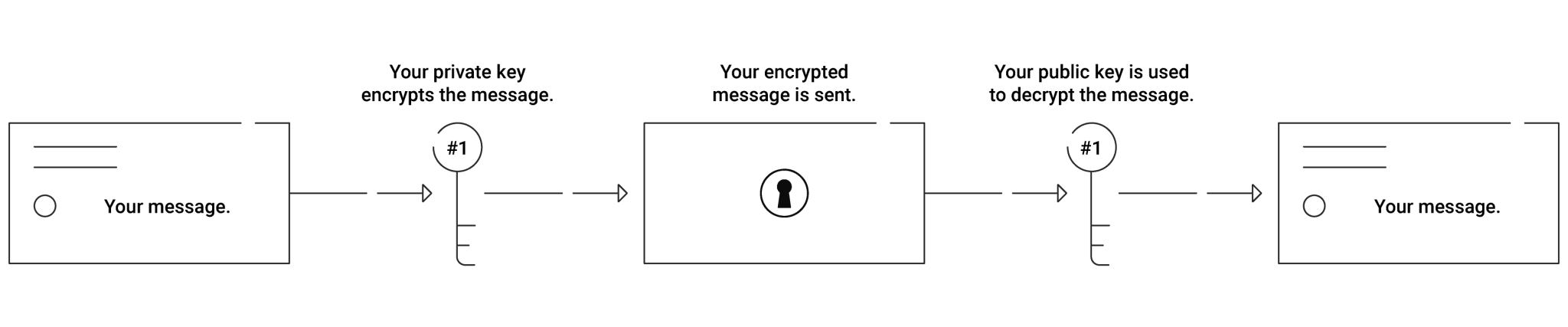
2. 加密 (Encryption)
假设A想向B发送消息M。A需要知道B的公钥(N, e)。
A将消息M(先通过某种方式转换成一个小于N的整数)进行加密,得到密文C:
![]()
原理: 模幂运算是一个单向函数。即使知道C, e, N,在不知道d或p, q的情况下,想要从C中求出M是非常困难的。
3. 解密 (Decryption)
B收到密文C后,使用自己的私钥指数d进行解密,还原出原始消息M:
![]()
原理: 由于d和e是特殊的逆元关系,根据欧拉定理,这个模幂运算可以完美地还原原始数据。d就是那个打开“陷门”的秘密钥匙。
![]()
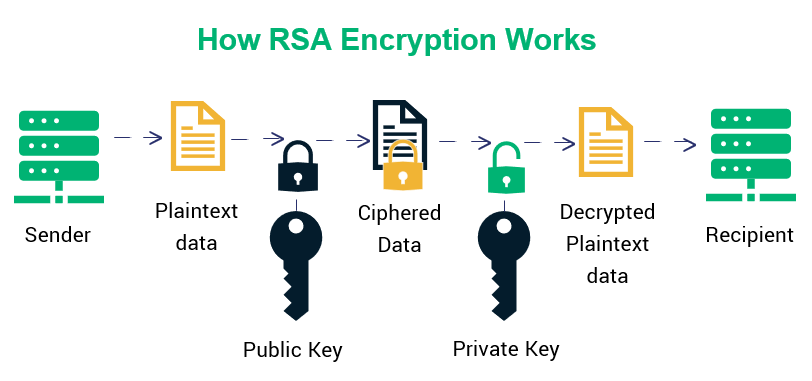
4. RSA的另一应用:数字签名
RSA算法的伟大之处在于它的可逆性——公钥可以加密,私钥可以解密;反过来,私钥也可以“加密”(即签名),公钥可以“解密”(即验证)。
数字签名是RSA的另一项核心功能。如果用户A用自己的私钥对一段信息进行加密,任何持有A的公钥的人都可以解密并验证。由于私钥只有A拥有,这证明了信息确实来源于A,从而实现了不可否认性和身份认证。这为电子商务和安全通信奠定了信任的基础。
5. 核心技术的地位与挑战
RSA算法的成功是史无前例的。从在线购物的安全套接层(SSL/TLS)握手,到SSH远程登录,再到VPN连接,RSA构成了现代网络安全体系的骨架。
然而,RSA的安全性完全取决于因数分解的困难性。随着量子计算理论的发展,肖尔算法(Shor's algorithm)被证明可以在理论上以极快的速度破解RSA。因此,密码学界正在积极寻找“后量子密码学”(Post-Quantum Cryptography)的新标准,以应对未来的挑战。
RSA的成功也让更多数学家投入密码学的发展,将算法的强度与数学难题结合起来,从而使算法具有了可用数学解释的、科学验证的健壮性。
回到我们谈到的1977年诞生的RSA算法,至今仍是“不解之谜”的代名词。它以数学的优雅和力量,将信任和保密性融入了全球数字基础设施,彻底改变了人类通信和交易的方式。
它的贡献,如同它所依赖的质数一样,是数字世界中最基础、最坚不可摧的存在。
