Leetcode 48

1 题目

114. 二叉树展开为链表

给你二叉树的根结点 root ，请你将它展开为一个单链表：

• 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
• 展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

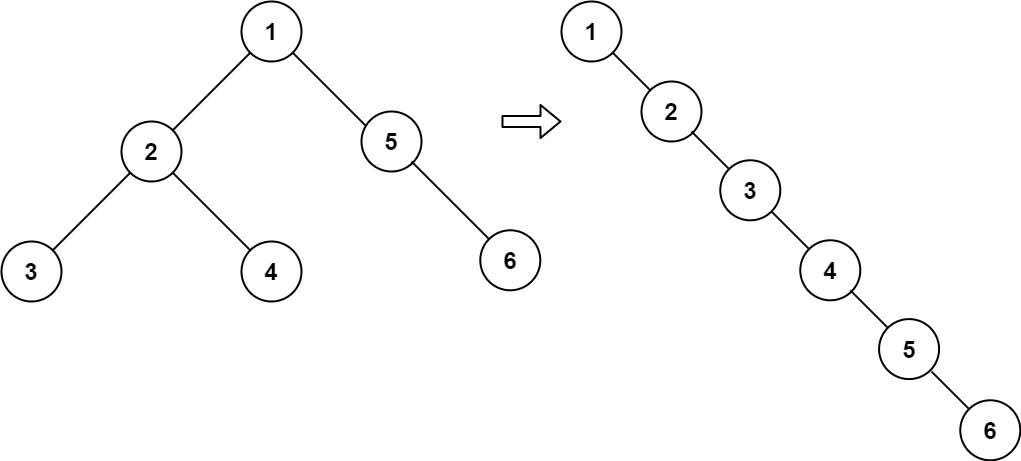
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [0]
输出：[0]

提示：

• 树中结点数在范围 [0, 2000] 内
• -100 <= Node.val <= 100

进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

2 代码实现

c

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/
typedef struct TreeNode TreeNode ;
void flatten(struct TreeNode* root) {if (root == NULL){return;}flatten(root -> left);flatten(root -> right);TreeNode *left = root -> left ;TreeNode *right = root -> right ;root -> left = NULL ;root -> right = left ;TreeNode *p = root ;while( p->right != NULL){p = p -> right;}p -> right = right;}

cpp

class Solution {
public:// 定义：将以 root 为根的树拉平为链表void flatten(TreeNode* root) {// base caseif (root == nullptr) return;// 利用定义，把左右子树拉平flatten(root->left);flatten(root->right);// *** 后序遍历位置 ***// 1、左右子树已经被拉平成一条链表TreeNode* left = root->left;TreeNode* right = root->right;// 2、将左子树作为右子树root->left = nullptr;root->right = left;// 3、将原先的右子树接到当前右子树的末端TreeNode* p = root;while (p->right != nullptr) {p = p->right;}p->right = right;}
};

这道题是要把一棵二叉树 "拉平" 成一个链表，要求链表的顺序和二叉树的前序遍历结果一致（根节点 -> 左子树 -> 右子树）。我们来一步步拆解这个解法的思路和执行过程。

核心思路

这个解法用后序遍历的思路解决问题：

1. 先把左子树拉平成链表
2. 再把右子树拉平成链表
3. 最后把左子树链表接到根节点右边，再把原右子树链表接到左子树链表的末端

详细步骤拆解

假设我们有这样一棵二叉树：

    1/ \2   5/ \   \
3   4   6

步骤 1：明确函数定义

flatten(TreeNode* root) 的作用是：将以 root 为根的二叉树，拉平成一个链表（链表中节点的 right 指针指向 "下一个节点"，left 指针为 null）。

步骤 2：base case

如果root == nullptr（空树），直接返回，不需要任何操作。

步骤 3：递归处理左右子树

先递归处理左子树，再递归处理右子树：

flatten(root->left);  // 把左子树拉平
flatten(root->right); // 把右子树拉平

• 对左子树（节点 2）递归后，左子树会变成：2 -> 3 -> 4（每个节点的 left 为 null，right 指向下一个）
• 对右子树（节点 5）递归后，右子树会变成：5 -> 6

步骤 4：拼接链表（后序遍历位置的关键操作）

此时左右子树已经都是链表了，接下来要把它们接到根节点后面：

① 保存左右子树的头节点

TreeNode* left = root->left;  // 左子树链表的头节点（2）
TreeNode* right = root->right; // 右子树链表的头节点（5）

② 将左子树链表接到根节点的右边

root->left = nullptr;    // 左指针置空（链表没有左孩子）
root->right = left;      // 根节点的右指针指向左子树链表的头（2）

此时树变成：

1 -> 2 -> 3 -> 4（原左子树链表）
原右子树5->6暂时游离

③ 将原右子树链表接到当前右子树的末端

需要先找到当前右子树（即原左子树链表）的最后一个节点（4），再把原右子树链表接上去：

TreeNode* p = root;
while (p->right != nullptr) {  // 循环找到当前右子树的最后一个节点p = p->right;
}
p->right = right;  // 最后一个节点的右指针指向原右子树链表的头（5）

最终结果：

1 -> 2 -> 3 -> 4 -> 5 -> 6

为什么用后序遍历？

因为拉平的操作（拼接链表）必须在左右子树都已经拉平之后才能进行。就像搭积木，必须先把左右两块积木各自拼好，才能把它们接到主体上。

总结执行流程

1. 递归到最底层的叶子节点，先把它们的左右子树（空）处理完
2. 从叶子节点开始，逐层向上拼接：左子树链表 -> 接到根节点右边 -> 原右子树链表 -> 接到左子树链表末端
3. 最终整棵树被拉成一个符合前序遍历顺序的链表

通过这种 "先解决子问题，再合并子问题结果" 的思路，高效地完成了二叉树到链表的转换。

【直接说明白为啥这个flatten能实现比较困难，feel一下】

确实，第一次看这个 flatten 函数会觉得 “绕”，难在它的逻辑是 “反直觉” 的 —— 明明要实现 “前序遍历顺序” 的链表，却用了 “后序遍历” 的执行顺序，而且整个过程像在 “拆了东墙补西墙”，得靠 “感觉” 慢慢悟。

可以试着这样 “感受” 它的过程：

想象你手里有一棵二叉树的模型，每个节点都有左右两根 “树枝”（左子树、右子树）。你的目标是把这棵树掰成一条直线（链表），顺序必须是 “根→左→右”，而且只能用右树枝连接（左树枝要掰断）。

怎么掰？你不能直接从根开始硬掰，因为左子树和右子树还没整理好，硬掰会乱。所以你得先把 “左子树” 掰成一条直线（递归处理左子树），再把 “右子树” 也掰成一条直线（递归处理右子树）。这两步就像先把两个 “小乱麻” 捋顺，变成两根 “直绳”。

等左右都捋顺了，就到了最关键的一步：

1. 把根节点的左树枝掰断（左指针置空），把左子树那根 “直绳” 接到根的右树枝上（根的右指针指向左子树）。
2. 然后顺着这根刚接好的右绳往下滑（循环找右子树末端），滑到最底端后，再把右子树那根 “直绳” 接上去。

整个过程就像：先把左右两个 “局部” 整理好，再把它们按顺序 “挂” 到根节点后面。你不用操心每一步具体怎么拆，只需要相信 “递归能把小的子树整理好”，最后专注于 “拼接” 就行。

这种 “先处理子问题，再合并结果” 的思路，有点像拼积木：先把零件各自拼好，再按顺序组装成整体。

一开始会觉得 “反着来”，但多看几遍具体例子的拼接过程，慢慢就会有 “哦，原来它是这么一步步把树‘捋直’的” 这种感觉了。