当前位置：首页 > news >正文

拉普拉斯算子及散度

news 2025/11/7 9:59:22

前置概念：

通量衡量的是向量场穿过一个表面的"总量"。数学上定义为：

$\phi = \int \int_SF \cdot n d_S$

其中：

$F$ 是向量场
$n$ 是表面的单位法向量
$d_S$ 是面积微元
$F\cdot n$ 是向量场在法向方向的投影

散度是一个标量，它描述了一个向量场在某一点处的“发散”程度。它衡量了一个函数在某一点的值与其周围点的平均值之间的差异。

假设有一个向量场 $F(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z))$ ，那么在点 $(x_0,y_0,z_0)$ 处的散度可以表示为：

$\triangledown \cdot F=\frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}$
拉普拉斯算子
拉普拉斯算子定义为梯度的散度： $\Delta f=\triangledown \cdot(\triangledown f)$
即对梯度向量场求散度
$\triangledown \cdot(\triangledown f)=\frac{\partial^2f}{\partial x^2}+\frac{\partial^2f}{\partial y^2}+\frac{\partial^2f}{\partial z^2}$
梯度 $(\bigtriangledown f)$ ：是一个向量场，指向函数值增长最快的方向，大小表示增长率。它描述了函数的“斜率”或“变化方向”。
散度 $(\bigtriangledown \cdot F)$ ：作用于一个向量场，衡量在一点处，该向量场是“发散”还是“汇聚”。正散度表示该点是场的“源”，负散度表示是“汇”。
首先求 f 的梯度，得到向量场 $\bigtriangledown f$ 。这个场表示 f 在每个点的变化趋势。
然后求这个梯度场的散度，即 $\bigtriangledown \cdot (\bigtriangledown f)$ 。
这意味着：拉普拉斯算子衡量的是，函数 f 的梯度场在一点处的“源强度”或“汇强度”。
- 如果 $\Delta f > 0$ ，说明在这一点，梯度场是“发散”的，意味着周围点的梯度向量都指向外，导致该点的函数值相对较低。
- 如果 $\Delta f < 0$ ，说明在这一点，梯度场是“汇聚”的，意味着周围点的梯度向量都指向内，导致该点的函数值相对较高。
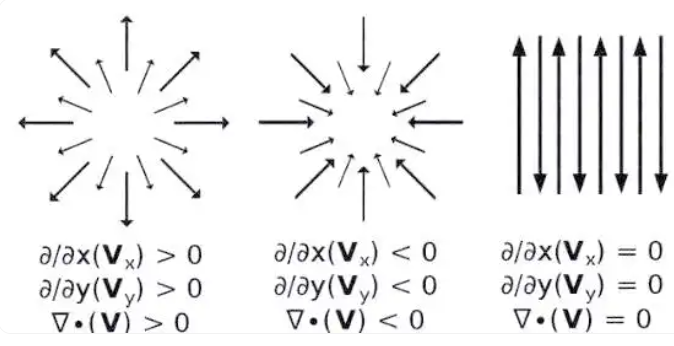
- 散度公式的推导
- 基本思路
  我们要计算在点 $P(x_0,y_0,z_0)$ 处，向量场 $F=(F_x,F_y,F_z)$ 沿X方向的净流出量。
  核心思想：在点 $P$ 处想象一个无穷小的立方体，计算通过这个立方体垂直于 $x$ 轴的两个面的流量差。
- 详细计算步骤
  步骤1：建立无穷小立方体
  以点 $P(x_0,y_0,z_0)$ 为中心，建立一个边长为 $\Delta x$ , $\Delta y$ , $\Delta z$ 的无穷小立方体：
- 左面： $x=x_0- \frac{\Delta x}{2}$
- 右面： $x=x_0+\frac{\Delta x}{2}$
- 其他面类似定义
- 立方体体积： $\Delta V=\Delta x \cdot \Delta y \cdot \Delta z$
  步骤2：计算通过右侧面的流出量
  右侧面位于 $x=x_0+\frac{\Delta x}{2}$ ，面积 $=\Delta y\cdot \Delta z$
  通过右侧面流出的流量 = 向量场在右侧面的 $x$ 分量 × 面积
  流出量右 $=F_x(x_0+\frac{\Delta x}{2},y_0,z_0)\cdot \Delta y \Delta z$
  注意：我们只关心 $x$ 分量 $F_x$ ，因为只有 $x$ 分量才会穿过垂直于 $x$ 轴的面。
  步骤3：计算通过左侧面的流入量
  左侧面位于 $x=x_0 - \frac{\Delta x}{2}$ ，面积 = $\Delta y \Delta z$
  通过左侧面流入的流量 = 向量场在左侧面的 $x$ 分量 × 面积
  流入量左= $F_x(x_0-\frac{\Delta x}{2}, y_0, z_0)\cdot \Delta y\Delta z$
  注意：这是流入量（正值），但净流出应该是流出减流入。
  步骤4：计算 $x$ 方向的净流出量
  $x$ 方向净流出量 = 流出量(右) - 流入量(左)
  净流出 $=[F_x(x_0+\frac{\Delta x}{2},y_0,z_0)-F_x(x_0-\frac{\Delta x}{2},y_0,z_0)]\Delta y \Delta z$
  步骤5：转换为单位体积的净流出
  为了得到单位体积的净流出，我们除以体积 $\Delta V=\Delta x \Delta y \Delta z$ ：
  净流出 $/\Delta V=\frac{F_x(x_0+\frac{\Delta x}{2},y_0,z_0)-F_x(x_0-\frac{\Delta x}{2},y_0,z_0)}{\Delta x}$
  步骤6：取极限得到精确值
  当立方体收缩到点 $P$ 时 $(\Delta x \to 0)$ ，上面的表达式正好是偏导数的定义：
  $\lim_{\Delta x \to 0} \frac{F_x(x_0+\frac{\Delta x}{2},y_0,z_0)-F_x(x_0-\frac{\Delta x}{2},y_0,z_0)}{\Delta x}=\frac{\partial F_x}{\partial x}(x_0, y_0, z_0)$
  最终结果
  在点 $P(x_0, y_0, z_0)$ 处，向量场 $F$ 沿 $x$ 轴的净流出（单位体积）为：
  $\frac{\partial F_x}{\partial x}(x_0, y_0, z_0)$
  几何解释
  这个结果有很直观的几何意义：
- 如果 $\frac{\partial F_x}{\partial x}>0$ ：当我们在x方向移动时， $F_x$ 在增加
  - 意味着右侧面的流出 > 左侧面的流入
  - $x$ 方向有净流出，对总散度做正贡献
- 如果 $\frac{\partial F_x}{\partial x}<0$ ：当我们在x方向移动时， $F_x$ 在减少
  - 意味着右侧面的流出 < 左侧面的流入
  - $x$ 方向有净流入，对总散度做负贡献
- 如果 $\frac{\partial F_x}{\partial x}=0$ ： $F_x$ 在 $x$ 方向不变
  - 流出 = 流入
  - $x$ 方向无净流量
- 完整散度的构成
  同理可得 $y$ 方向和 $z$ 方向的贡献：
- $y$ 方向： $\frac{\partial F_y}{\partial y}$
- $z$ 方向： $\frac{\partial F_z}{\partial z}$
- 总散度 = 三个方向的净流出之和：
  $\triangledown \cdot F = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} +\frac{\partial F_z}{\partial z}$