MATLAB基于Theil不等系数的IOWHA算子组合预测模型
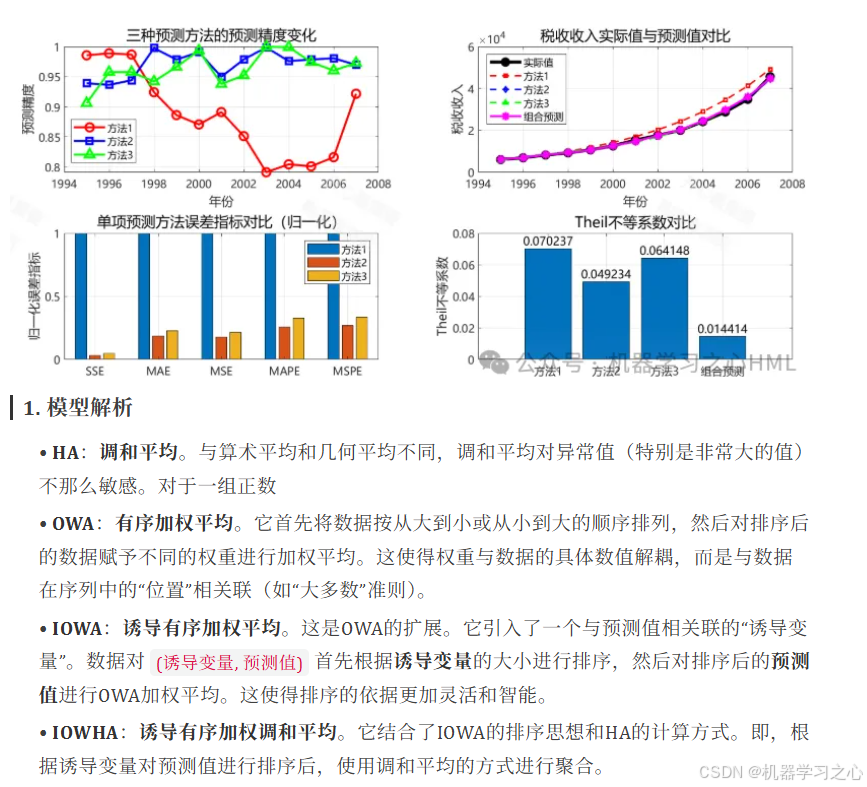
1. 模型解析
1.1 IOWHA 算子
-
HA:调和平均。与算术平均和几何平均不同,调和平均对异常值(特别是非常大的值)不那么敏感。对于一组正数
-
OWA:有序加权平均。它首先将数据按从大到小或从小到大的顺序排列,然后对排序后的数据赋予不同的权重进行加权平均。这使得权重与数据的具体数值解耦,而是与数据在序列中的“位置”相关联(如“大多数”准则)。
-
IOWA:诱导有序加权平均。这是OWA的扩展。它引入了一个与预测值相关联的“诱导变量”。数据对
(诱导变量, 预测值)首先根据诱导变量的大小进行排序,然后对排序后的预测值进行OWA加权平均。这使得排序的依据更加灵活和智能。 -
IOWHA:诱导有序加权调和平均。它结合了IOWA的排序思想和HA的计算方式。即,根据诱导变量对预测值进行排序后,使用调和平均的方式进行聚合。
1.2 Theil不等系数
Theil不等系数是衡量预测精度的经典指标,用于比较预测值与实际值的接近程度。
2. 组合预测
这个模型的巧妙之处在于,它使用Theil不等系数作为IOWHA算子的诱导变量。
模型构建步骤
假设:
- 有 ( m ) 种单一的预测方法。
- 时间跨度 ( t = 1, 2, …, n )。
- ( y_t ) 是t时刻的实际观测值。
- ( f_{it} ) 是第 ( i ) 种预测方法在t时刻的预测值。
- 目标是找到t时刻的组合预测值 ( F_t )。
步骤 1:计算各单项预测模型的Theil不等系数
步骤 2:确定诱导变量和排序
步骤 3:定义位置权重并应用IOWHA算子
3. 模型特点
- 动态自适应:权重不是固定的,而是根据每个模型在最近一期的表现动态调整。这使模型能快速适应数据模式的变化。
- 突出优秀模型:通过将Theil系数或近期误差作为诱导变量,并对其进行排序,确保了在上一期表现更好的模型其预测值在计算组合值时占据更重要的位置(通过分配更大的权重 ( w_k ) 给靠前的位置)。
- 稳健性强:
- 调和平均的稳健性:调和平均对异常大的预测值具有“惩罚”效应。即使某个模型给出了一个极不合理的预测值,由于其倒数很小,在调和平均的计算中会被严重削弱影响力。
- IOWA的稳健性:权重与数据值本身解耦,只与诱导变量决定的顺序有关,避免了极端数据值直接获得极端权重。
- 理论基础坚实:结合了误差度量指标(Theil)和信息聚合算子(IOWHA)的优势,逻辑清晰,可解释性强。
4. 总结
基于Theil不等系数的IOWHA算子组合预测模型是一个精妙的“元学习”框架。它的核心思想是:
“相信在最近时刻犯错误最小的模型,并且在综合所有模型意见时,采用一种对极端意见持保守态度的方式(调和平均)。”
通过将Theil不等系数或近期预测误差作为诱导变量,模型实现了对单项预测模型的动态、性能导向的排序。再通过IOWHA算子,模型以一种稳健的方式融合了这些排序后的预测信息,从而通常能够获得比任何单一模型或简单平均组合更优越的预测性能。
