算法 day 45

不同的子序列

这个题的递推公式很难想，在评论区发现了一个更好理解的思路：

假设当前遍历到的 t 是 bag，s 是 babga，此时 s 又来了一个 g， 和当前 t 的最后一个元素相同了。这个时候新的 babgag 含有 bag 的数量是在 babga 原本包含的 bag 数量（dp【i - 1】【j】）的基础上，增加了使用新来的 g 新组成的 bag 数量。新来的 g 能组成多少个bag，其实是原本的 babga 包含多少个 ba。也就是 dp【i - 1】【j - 1】。

class Solution {
public:int numDistinct(string s, string t) {vector<vector<uint64_t>> dp(s.size()+1,vector<uint64_t>(t.size()+1));for(int i =0;i<s.size();i++) dp[i][0]=1;for(int j =1;j<t.size();j++) dp[0][j]=0;for(int i=1;i<=s.size();i++){for(int j=1;j<=t.size();j++){if(s[i-1]==t[j-1]) dp[i][j]=dp[i-1][j-1]+dp[i-1][j];else dp[i][j]=dp[i-1][j];}}return dp[s.size()][t.size()];}
};

两个字符串的删除操作

这个题就还是那个公共子序列的题目，递推公式反而还好想一些。可能是对这一块稍微熟悉了一点，另外就是个人感觉：【i-1】【j】和【i】【j-1】两个不同的情况其实不用分那么仔细：

情况一：删word1[i - 1]，最少操作次数为dp[i - 1][j] + 1

情况二：删word2[j - 1]，最少操作次数为dp[i][j - 1] + 1

情况三：同时删word1[i - 1]和word2[j - 1]，操作的最少次数为dp[i - 1][j - 1] + 2

那最后当然是取最小值，所以当word1[i - 1] 与 word2[j - 1]不相同的时候，递推公式：dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});

但其实融合一下下就可以发现，按照dp表的推导顺序，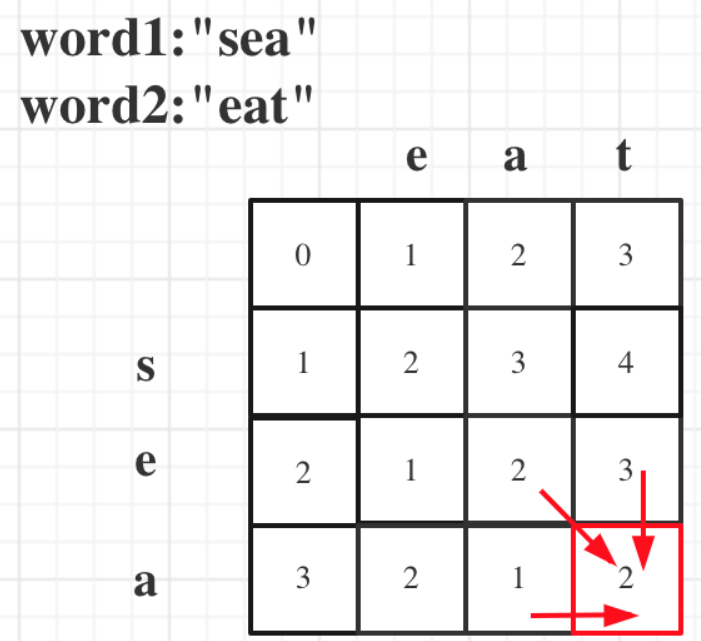

其实归纳为两个方向，一个是从上到下，一个是从左到右，也就成了 最后的简化形式。

dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);

其中前半部分表示的是行的从左向右，后半部分表示的是列的从上到下，这也印证了第四步的遍历顺序。

class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1));for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;for (int i = 1; i <= word1.size(); i++) {for (int j = 1; j <= word2.size(); j++) {if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);}}}return dp[word1.size()][word2.size()];}
};

编辑距离

好像是打boss的题一样，但是前面顺下来，这道题真就还好了。min的三个dp元素居然要大括号括起来...

此外，需要注意一下看似很繁杂的增删改操作，其实就是dp的三种状态转移，这样的转化非常巧妙。我进化了。（？）

class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>> dp(word1.size()+1,vector<int>(word2.size()+1));for(int i =0;i<=word1.size();i++) dp[i][0] = i;for(int j =0;j<=word2.size();j++) dp[0][j] = j;for(int i =1;i<=word1.size();i++){for(int j =1;j<= word2.size();j++){if(word1[i-1]==word2[j-1]){dp[i][j]=dp[i-1][j-1];}else{dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;}}}return dp[word1.size()][word2.size()];}
};