算法题（Python）数组篇 | 3.有序数组的平方

一、题目描述

给你一个按非递减顺序排序的整数数组nums，返回每个数字的平方组成的新数组，要求也按非递减顺序排序。
示例1：

输入：nums = [-4, -1, 0, 3, 10]
输出：[0, 1, 9, 16, 100]
解释：平方后，数组变为[16, 1, 0, 9, 100]，排序后，数组变为[0, 1, 9, 16, 100]

示例2：

输入：nums = [-7, -3, 2, 3, 11]
输出：[4, 9, 9, 49, 121]

提示：

1 <= nums.length <= 10000
-10000 <= nums[i] <= 10000
nums已按非递减顺序排序

二、题解

2.1 解法一：暴力解法

最直观的想法莫过于：每个数平方之后，排个序，代码如下：

class Solution:def sortedSquares(self, nums: List[int]) -> List[int]:for i in range(len(nums)):nums[i] *= nums[i]nums.sort()return nums

2.2 解法二：双指针法

数组本身是有序的，只是负数平方之后可能会成为最大数。那么数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间。此时可以考虑双指针法，i指向起始位置，j指向终止位置。
定义一个新数组result，和输入数组A的大小一样，让k指向result数组的终止位置。
如果$A[i]\ast A[i]<A[j]\ast A[j]$，那么$result[k--]=A[j]\ast A[j]$
如果$A[i]\ast A[i]>=A[j]\ast A[j]$，那么$result[k--]=A[i]\ast A[i]$
如下图所示：


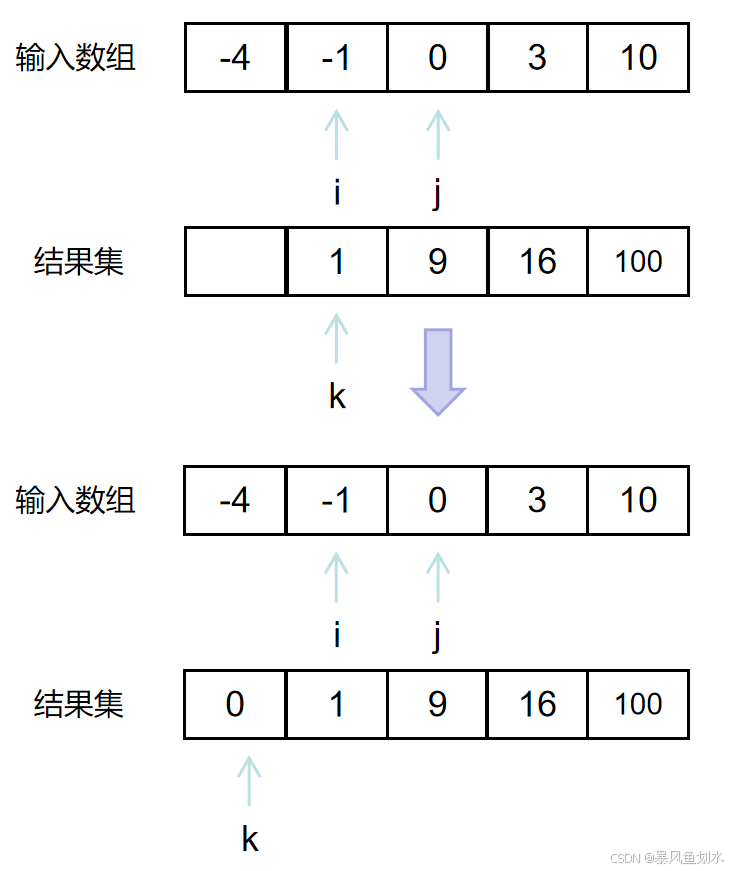
代码如下：

class Solution:def sortedSquares(self, nums: List[int]) -> List[int]:i, j, k = 0, len(nums) - 1, len(nums) - 1res = [float('inf')] * len(nums)  # 需提前定义列表，存放结果while i <= j:if nums[i] ** 2 <= nums[j] ** 2:  # 左右指针所指向的值的平方的大小比较res[k] = num[j] ** 2j -= 1    # 右指针向左移动else:res[k] = nums[i] ** 2i += 1   # 左指针向右移动k -= 1   # 结果指针向左移动return res