【深度强化学习】#6 Soft Actor-Critic：最大熵与重参数化技巧

从DDPG到TD3，Actor-Critic方法围绕确定性策略在处理连续动作空间问题上走向了高峰，但确定性策略这一核心也成为了其进一步发展的瓶颈。在确定性策略下，智能体的探索严重依赖人为添加到动作的外部噪声，既引入了更繁琐的超参数调优，又从本质上限制了智能体在复杂环境中进行多样化探索的能力。为此，SAC应运而生。

SAC

SAC（Soft Actor-Critic，软演员-评论家）继承了TD3的技术精华，并将其转换为随机性策略的范式，从而提升了探索能力、样本效率和稳定性。

最大熵强化学习

SAC首先通过最大熵强化学习解决了策略网络在训练过程中逐渐降低探索性的问题。

最大熵强化学习向目标函数引入了策略的熵，用于衡量策略的随机性。对于原始的策略梯度，其目标是最大化期望累积奖励

$$J(\theta )={\mathbb{E}}_{(s_t,a_t)\sim {\rho }_{\pi }}\left[\sum _{t=0}^T{\gamma }^{t}r(s_t,a_t)\right]$$

而SAC的目标是在最大化累积奖励的同时，最大化策略的熵，以鼓励探索

$$J(\theta )={\mathbb{E}}_{(s_t,a_t)\sim {\rho }_{\pi }}\left[\sum _{t=0}^T{\gamma }^t(r(s_t,a_t)+\alpha \mathcal{H}({\pi }_{\theta }(\cdot |s_t)))\right]$$

其中$\mathcal{H}(\pi (\cdot |s))$是策略$\pi$在状态$s$下的熵

$$\begin{array}{rl}\mathcal{H}(\pi (\cdot |s))& =-{\mathbb{E}}_{a\sim \pi }[\log \pi (a|s)]\\ & =-\int \pi (a|s)\log \pi (a|s)\mathrm{d}a\end{array}$$

观察$-x\log x$（以2为底）的函数图像，可知最大化策略的熵的效果就是让动作的概率向“中间”靠拢，即趋于均匀分布。随着底数的增大，函数的极值将变小，最大化目标对策略随机性的激励强度也将变小。

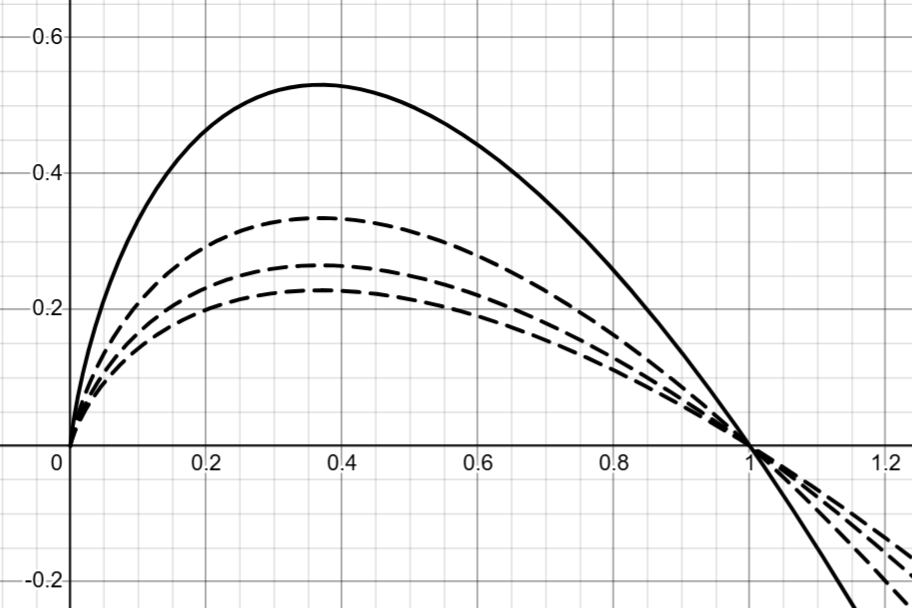
根据对数换底公式，底数的影响可以被吸收进温度参数$\alpha$中。$\alpha$越大，目标越鼓励策略的随机性，而底数在实际实现中通常采用自然常数$e$。温度系数$\alpha$最简单的设置方法即手动调优，根据不同问题下策略的收敛速度和随机性设定。现代SAC常用自动熵调整，通过最小化损失函数$L(\alpha )=\alpha (\log \pi (a|s)+\tilde{\mathcal{H}})$学习，其中$\tilde{\mathcal{H}}$是人为设定的目标熵，根据经验通常设为$-\dim (\mathcal{A})$，即负的动作空间维度，以鼓励策略在每个动作维度上接近均匀分布。

对于新的策略评估方式，SAC也定义了新的Q函数，称为soft Q函数

$$Q_{\mathrm{soft}}^{\pi }(s_t,a_t)\dot{=}{\mathbb{E}}_{(s_t,a_t)\sim {\rho }_{\pi }}\left[r(s_t,a_t)+\sum _{k=1}^T{\gamma }^k(r(s_{t+k},r_{t+k})+\alpha \mathcal{H}(\pi (\cdot |s_{t+k})))\right]$$

soft Q函数将策略的熵同样视为一种奖励，融入在$s_t$执行动作$a_t$后能获得的期望累积回报当中，而Critic网络也将直接学习如何给出soft Q函数的估计值。soft Q函数不包含$\alpha \mathcal{H}(\pi (\cdot |s_t))$，是因为它由$s_t$决定而与$a_t$无关。

现在，我们可以将目标函数写为

$$J(\theta )={\mathbb{E}}_{s\sim {\rho }_{\pi },a\sim {\pi }_{\theta }}\left[Q_{\mathrm{soft}}^{\pi }(s,a)+\alpha \mathcal{H}({\pi }_{\theta }(\cdot |s))\right]$$

（关于目标函数的状态-动作是否带下标t，这取决于我们是从整条轨迹的视角，还是从静态分布的视角来理解。通常轨迹视角使用求和形式，而静态分布视角使用价值函数形式）

根据策略梯度定理的一般形式，我们有目标函数的梯度

$${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{s\sim {\rho }_{\pi },a\sim {\pi }_{\theta }}\left[{\nabla }_{\theta }\ln {\pi }_{\theta }(a|s)Q_{\mathrm{soft}}^{\pi }(s,a)]+{\mathbb{E}}_{s\sim {\rho }_{\pi }}[{\nabla }_{\theta }\alpha \mathcal{H}({\pi }_{\theta }(\cdot |s))\right]$$

重参数化技巧

SAC又利用重参数化技巧从动作采样这一根源上降低了方差。

在DPG一章中，我们推导出确定性策略梯度定理如下

$${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{s\sim {\rho }^{{\mu }_{\theta }}}[{\nabla }_{\theta }{\mu }_{\theta }(s){\nabla }_a{Q}^{{\mu }_{\theta }}(s,a){|}_{a={\mu }_{\theta }(s)}]$$

但是在Actor-Critic一章中，同样对于Q函数，我们使用的随机性策略梯度定理为

$${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{s\sim {\rho }_{\pi },a\sim {\pi }_{\theta }}[{\nabla }_{\theta }\ln {\pi }_{\theta }(a|s)Q(s,a)]$$

对比发现，之前的随机性策略算法只关注了$\theta$对${\pi }_{\theta }$的梯度，却没有利用$\theta \to {\pi }_{\theta }\to a\to Q(s,a)$这条路径的梯度。这是因为在随机性策略梯度的推导中，我们用采样得到的回报$G(\tau )$代替了真实函数$Q(s,a)$，二者在期望意义下是等价的。如果直接计算$Q(s,a)$对$a$的梯度，我们就无法消去环境动态特性$p(s_{t+1}|s_t,a_t)$，进而无法将梯度算符$\nabla$移到期望中，而环境动态特性通常是未知的。但是放弃利用动作梯度的信息而仅仅依赖采样拟合的代价就是高方差。

重参数化技巧通过规范策略的参数化形式，切断了采样随机性和策略网络参数$\theta$之间的关系，打通了一条完全确定的梯度传播路径。我们通常采用高斯分布作为策略的形式，因为这符合我们对连续控制任务的直觉，也易于数学上的计算和随机性的调节。此时动作的分布为

$$a\sim \mathcal{N}({\mu }_{\theta }(s),{\sigma }_{\theta }(s{)}^2)$$

策略网络将以状态$s$为输入，输出高斯分布的均值$\mu$和标准差$\sigma$。而为了让随机性与参数$\theta$无关，我们变换该分布如下

KaTeX parse error: Too many tab characters: & at position 83: …s)\cdot\epsilon&̲\\ &\quad\epsil…

由此，我们不再直接采样动作$a$，而是先从一个固定的、与参数$\theta$无关的基础分布（如标准正态分布$\mathcal{N}(0,1)$）中采样一个随机噪声$ϵ$，再通过一个确定的、可微的变换构造出动作$a$。

策略梯度推导

结合重参数化技巧，我们重新得到SAC的目标函数为

$$\begin{array}{rl}J(\theta )& ={\mathbb{E}}_{s\sim {\rho }_{\pi },ϵ\sim \mathcal{N}}\left[Q_{\mathrm{soft}}^{\pi }(s,f_{\theta }(ϵ;s))+\alpha \mathcal{H}({\pi }_{\theta }(f_{\theta }(ϵ;s)|s))\right]\\ & ={\mathbb{E}}_{s\sim {\rho }_{\pi },ϵ\sim \mathcal{N}}\left[Q_{\mathrm{soft}}^{\pi }(s,f_{\theta }(ϵ;s))-\alpha \log {\pi }_{\theta }(f_{\theta }(ϵ;s)|s)\right]\end{array}$$

需要辨析的是，$f_{\theta }(ϵ;s)$和${\pi }_{\theta }$都源于同一个策略，区别在于$f_{\theta }(ϵ;s)$是一个动作生成器，负责采样；而${\pi }_{\theta }$是一个概率分布函数，负责评估动作的概率。

现在SAC的策略梯度为

$$\begin{array}{rl}{\nabla }_{\theta }J(\theta )& ={\nabla }_{\theta }{\mathbb{E}}_{s\sim {\rho }_{\pi },ϵ\sim \mathcal{N}}\left[Q_{\mathrm{soft}}^{\pi }(s,f_{\theta }(ϵ;s))-\alpha \log {\pi }_{\theta }(f_{\theta }(ϵ;s)|s)\right]\\ & ={\mathbb{E}}_{s\sim {\rho }_{\pi },ϵ\sim \mathcal{N}}\left[{\nabla }_{\theta }(Q_{\mathrm{soft}}^{\pi }(s,f_{\theta }(ϵ;s))-\alpha \log {\pi }_{\theta }(f_{\theta }(ϵ;s)|s))\right]\end{array}$$

Soft Q函数的梯度根据链式法则有

$${\nabla }_{\theta }(Q_{\mathrm{soft}}^{\pi }(s,f_{\theta }(ϵ;s)))={\nabla }_a{Q}_{\mathrm{soft}}^{\pi }(s,a){|}_{a=f_{\theta }(ϵ;s)}\cdot {\nabla }_{\theta }{f}_{\theta }(ϵ;s)$$

熵的梯度

$${\nabla }_{\theta }(-\alpha \log {\pi }_{\theta }(f_{\theta }(ϵ;s)|s))=-\alpha {\nabla }_{\theta }\log {\pi }_{\theta }(f_{\theta }(ϵ;s)|s)$$

$\log {\pi }_{\theta }(f_{\theta }(ϵ;s)|s)$是$a$和$\theta$的函数，同样根据链式法则有

$${\nabla }_{\theta }\log {\pi }_{\theta }(f_{\theta }(ϵ;s)|s)={\nabla }_{\theta }\log {\pi }_{\theta }(a|s){|}_{a=f_{\theta }(ϵ;s)}+{\nabla }_a\log {\pi }_{\theta }(a|s){|}_{a=f_{\theta }(ϵ;s)}\cdot {\nabla }_{\theta }{f}_{\theta }(ϵ;s)$$

其中第一项是保持动作$a$不变时，策略概率关于$\theta$的梯度；第二项是$\theta$引起动作$a$改变对策略概率的梯度。

第一项梯度对于任意给定的状态$s$期望为零，证明如下

$$\begin{array}{rl}{\mathbb{E}}_{a\sim {\pi }_{\theta }}[{\nabla }_{\theta }\log {\pi }_{\theta }(a|s)]& =\int {\pi }_{\theta }(a|s)\cdot {\nabla }_{\theta }\log {\pi }_{\theta }(a|s)\mathrm{d}a\\ \text{（自然对数导数性质）}& =\int {\pi }_{\theta }(a|s)\cdot \frac{{\nabla }_{\theta }{\pi }_{\theta }(a|s)}{{\pi }_{\theta }(a|s)}\mathrm{d}a\\ & =\int {\nabla }_{\theta }{\pi }_{\theta }(a|s)\mathrm{d}a\\ \text{（梯度变量与积分变量不一致时，梯度算符可提出）}& ={\nabla }_{\theta }\int {\pi }_{\theta }(a|s)\mathrm{d}a\\ \text{（概率分布的归一化条件）}& ={\nabla }_{\theta }1=0\end{array}$$

最终我们得到SAC完整的策略梯度如下

$${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{s\sim {\rho }_{\pi },ϵ\sim \mathcal{N}}\left[({\nabla }_a{Q}_{\mathrm{soft}}^{\pi }(s,a){|}_{a=f_{\theta }(ϵ;s)}-\alpha {\nabla }_a\log {\pi }_{\theta }(a|s){|}_{a=f_{\theta }(ϵ;s)})\cdot {\nabla }_{\theta }{f}_{\theta }(ϵ;s)\right]$$

随机梯度更新采用的梯度则为

$${\nabla }_{\theta }J(\theta )=({\nabla }_a{Q}_{\mathrm{soft}}^{\pi }(s,a){|}_{a=f_{\theta }(ϵ;s)}-\alpha {\nabla }_a\log {\pi }_{\theta }(a|s){|}_{a=f_{\theta }(ϵ;s)})\cdot {\nabla }_{\theta }{f}_{\theta }(ϵ;s)$$

网络框架

在其他技术细节上，SAC继承了TD3算法。网络框架上，SAC拥有一个Actor网络和双Critic-Q网络，以及它们各自的目标网络，并且目标网络的更新方式为软更新。但研究表明TD3中的延迟策略更新在SAC中效果并不显著，甚至会减慢策略的适应速度进而降低性能，因此没有被采用。

每个Q网络$Q_{w_j}(s,a)$的目标值为（由目标网络计算）

$$y_t=r(s_t,a_t)+\gamma \left(\underset{j=1,2}{\min }{Q}_{w_j^{\prime }}^{\prime }(s_{t+1},f_{{\theta }^{\prime }}^{\prime }(ϵ;s_{t+1}))-\alpha \log {\pi }_{{\theta }^{\prime }}^{\prime }(f_{{\theta }^{\prime }}^{\prime }(ϵ;s_{t+1})|s_{t+1})\right)$$

Actor网络的策略梯度为（由主网络计算）

$${\nabla }_{\theta }J(\theta )=({\nabla }_a{Q}_{w_1}(s,a){|}_{a=f_{\theta }(ϵ;s)}-\alpha {\nabla }_a\log {\pi }_{\theta }(a|s){|}_{a=f_{\theta }(ϵ;s)})\cdot {\nabla }_{\theta }{f}_{\theta }(ϵ;s)$$

原始的SAC算法还使用了一个Critic-V网络，它用于估计Q网络除了$r(s_t,a_t)$的部分，进而计算Q网络的目标值

$$y=r(s_t,a_t)+\gamma V(s_{t+1})$$

而双Q网络则用于计算V网络的目标值。但这仅仅是为了构建贝尔曼方程的形式，实现理论上的优雅。后来作者发现V网络是多余的，移除V网络可以降低算法复杂度、避免更多估计误差，算法性能却相当甚至更好。

算法流程

SAC的算法流程如下：

1. 初始化
   1. Actor网络${\pi }_{\theta }(a|s)$和Critic网络$Q_{w_1}(s,a)$，$Q_{w_2}(s,a)$；
   2. 目标Actor网络${\pi }_{{\theta }^{\prime }}^{\prime }(a|s)$和目标Critic网络$Q_{w_1^{\prime }}^{\prime }(s,a)$，$Q_{w_2^{\prime }}^{\prime }(s,a)$，参数分别从主网络复制而来；
   3. 经验回放缓存区$R$；
   4. 超参数：温度系数$\alpha$，动作选择器噪声$ϵ\sim \mathcal{N}(0,I)$。
2. 循环（每一幕）
   1. 初始化状态$s_1$；
   2. 循环（每个时间步$t$）
      1. 由动作选择器（主网络）采样动作$a_t=f_{\theta }(ϵ;s_t)$，得到奖励$r_t$和后继状态$s_{t+1}$；
      2. 将转移样本$(s_t,a_t,r_t,s_{t+1})$存入回放缓冲区$R$；
      3. 如果样本数量$|R|⩾N$，则随机采样一个小批量的$N$个转移样本$(s_i,a_i,r_i,s_{i+1})$；
      4. 对每个转移样本$(s_i,a_i,r_i,s_{i+1})$，由动作选择器（目标网络）采样下一个动作$a_i^{\prime }=f_{{\theta }^{\prime }}^{\prime }(ϵ;s_{i+1})$，并计算其对数概率$\log {\pi }_{{\theta }^{\prime }}^{\prime }(a_i^{\prime }|s_{i+1})$；
      5. 计算样本批量的平均梯度更新每个Critic网络$$w_{t+1}^{(j)}=w_t^{(j)}-{\alpha }_{w^{(j)}}\frac{1}{N}\sum _{i=1}^N[(y_i-Q_{w^{(j)}}(s_i,a_i))\cdot {\nabla }_{w^{(j)}}{Q}_{w^{(j)}}(s_i,a_i)]$$
      6. 计算样本批量的平均梯度更新Actor网络$${\theta }_{t+1}={\theta }_t+{\alpha }_{\theta }\frac{1}{N}\sum _{i=1}^N{\nabla }_{\theta }{J}_i(\theta )$$
      7. 软更新目标网络$$\begin{array}{r}{\theta }^{\prime }\leftarrow \tau \theta +(1-\tau ){\theta }^{\prime }\\ w_j^{\prime }\leftarrow \tau w_j+(1-\tau )w_j^{\prime }\end{array}$$
3. 直到Actor网络和Critic网络收敛。