大数据成矿预测系列(六) | 从“看图像”到“读结构”:图卷积神经网络如何赋能地质“图谱”推理
前言
在前文中,我们介绍了卷积神经网络(CNN)为成矿预测带来了新的契机,并在一定程度上突破了传统机器学习模型的局限。卷积神经网络无疑扮演了先驱者的角色。其作为一种强大的“基于图像的模型” ,其核心优势在于能够像“看照片”一样处理和分析地质图件。
尽管在较为完善的特征工程支持下,卷积神经网络在多源异构数据集上的应用具有一定的可行性,但它仍存在一些难以克服的固有缺陷。正是为了应对这些挑战,我们引出了这一部分的主角——图卷积神经网络(GCN)。

CNN的成就: 栅格数据中的“像素智能”
CNN通过其“卷积核”设计,能够“提取局部的有意义特征并捕捉空间模式” 。无论是在遥感影像中自动进行岩性填图 ,还是在地球物理和地球化学栅格数据中识别环状或线性异常,CNN都展示了其强大的局部特征提取能力 。在三维(3D)成矿预测中,3D-CNN模型也能从3D预测层中提取空间分布特征 。
这种能力,我们可以称之为“像素智能”。CNN就像一位“近视”的图像专家,它能极其敏锐地识别小范围内的纹理和模式,例如在“短程区域”内提取丰富的光谱与空间特征 。

(1) “近视”的感知——受限的局部感受野
CNN的这种“近视”特性也构成了它的第一个“阿喀琉斯之踵”。早期的“像素级”模型完全忽略了空间关联性,它们“没有充分考虑相邻像素之间的空间关联” 。CNN通过其卷积核(如3x3或5x5)改进了这一点,但其本质仍然是“局部的”。
CNN的“卷积核局部感知”特性意味着它的“感受野”是固定的、有限的 。一个地质学家深知,两个相距5公里的钻孔可能因为同处一条区域性大断裂上而具有极强的成矿关联性。但对于一个感受野只有5x5像素的CNN来说,这两个点在空间上是“不相关”的,它永远无法“看到”它们之间的这种远距离联系。
(2) “读不懂”的结构——非欧空间数据的挑战
CNN的第二个,也是更根本的局限,在于它“读不懂”地质结构。CNN的算法设计要求输入数据是“规则的” ,即必须是像照片一样的“常规栅格输入” 。这种数据结构被称为“欧几里得空间”(Euclidean space)。
然而,地质学,尤其是构造地质学,其本质是非欧几里得(non-Euclidean)的 。地质图上的断裂网络、河流网络、岩体接触带,在数据结构上是“图”(Graphs),而不是“网格”(Grids)。3D地质模型的“非欧几里得和非结构化性质” 从根本上“禁止它们直接输入到CNN中” 。

这迫使地质学家和数据科学家们进行一种“拓扑妥协”。为了使用CNN,研究人员不得不将复杂的“3D地质数据重组为2D多通道图像” 。这无异于将一个复杂的三维断裂系统“压扁”成一系列二维切片,以此来“规避”CNN对输入格式的限制。这种妥协是巨大的:在分析开始之前,我们已经通过“手工艺”式的预处理 ,将数据的真实拓扑结构扭曲了。模型学习的,是一个已经失真的地质“快照”,而非地质“结构”本身。
这种局限性不仅仅在于距离,更在于连通性。CNN只能理解像素网格中的“邻近”,而无法理解地质网络中的“连接”。两个在地图上相距甚远但在同一条断裂带上的点,在CNN看来是无关的,但在地质学家和图卷积网络(GCN)看来,它们是“强相关”的 。这正是GCN作为“基于图”的模型 所要解决的核心问题。
GCN的“世界观”:万物皆“图”
GCN的出现,代表了一种根本性的“世界观”转变。它不再强迫地质数据去适应“网格”,而是提供了一种新的语言来描述地质数据本来的样子——“图”。
GCN是CNN在“非网格数据” 或“非欧几里得”数据上的自然延伸。它是一种“基于图的模型” ,其核心数据结构是一个“图”(Graph)。一个图由“节点”(Nodes,代表实体)和“边”(Edges,代表关系)组成 。
GCN的目标是“捕捉复杂和非线性的空间关系” ,它允许我们不再局限于像素的“上下左右”,而是根据地质学原理来定义数据点之间的“关系”。
如果说CNN是“近视的图像专家”,那么GCN就是一位“结构工程师”。它阅读的不是地质体的“照片”,而是地质系统的“结构蓝图”(即地质图谱)。
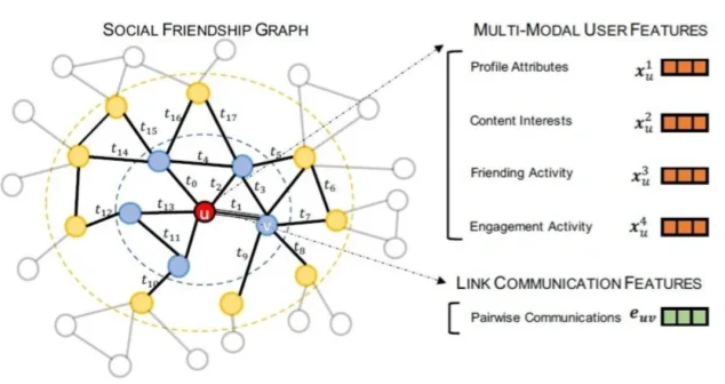
“地质图谱”的构建
将地质知识转化为GCN可以理解的“图谱”,是整个流程中最关键、最能体现地质学家价值的一步。这一步需要将“先验领域知识” 注入“拓扑图的构建” 过程中,有时也称为构建“地质知识图谱” 。
节点 (Nodes)
节点(Nodes)是我们分析的“实体”。节点的定义决定了分析的尺度和对象。
同质网格节点 (Homogeneous Grid Nodes) 这是从CNN过渡到GCN最直接的方式。将研究区划分为网格单元(例如 1km x 1km),每个“网格单元” 或“像素” 都被视为一个节点。这种情况下,“勘探信息...可以被视为图,其中像素通过其相邻像素连接” 。
异质实体节点 (Heterogeneous Entity Nodes) 这是一种更强大、更符合地质思维的方式。在一个“异质图” 中,节点可以代表“不同类型的地质实体” 。例如,一个图谱可以同时包含代表“一个岩体”、“一个矿点”、“一个钻孔” 乃至“一条断裂” 的不同类型的节点。
边 (Edges)
边(Edges)是GCN的精华所在,它们编码了节点之间的“关系” ,是“地质空间信息的关键编码” 。
空间邻近边 (Spatial Proximity Edges) 最基础的边。连接所有空间上“相邻”的节点,例如通过“K-近邻”算法 或连接所有“相邻像素” 来实现。这种边在某种程度上复制了CNN的局部视野。
结构连通边 (Structural Connectivity Edges) 这是GCN的“超能力”。它连接地质上相关、但空间上可能相距甚远的节点。例如,如上文所述,将“同在一条NNE向大断裂上的所有单元(即使不相邻)” 用边连接起来。这直接将地质学家的控矿假设(例如“NNE向断裂是导矿构造”)编码到了模型结构中。
岩性与接触边 (Lithological & Contact Edges) 连接所有“同属于XX花岗岩体”的节点。更进一步,我们甚至可以反向操作,例如删除那些“跨越...地质边界”的边 ,或者专门添加代表“地层接触关系”或“侵入接触带”的边。
相似性边 (Similarity Edges) 不基于物理空间,而是基于特征空间的连接。节点之间的边的“权重...基于两个节点的相关性” 或“相似性” 。例如,如果两个钻孔的“地球化学特征”高度相似,则在它们之间连接一条边。
为了清晰地展示“建图”这一步骤,下表示例总结了构建一个地质图谱的设计。
| 图组件 | 定义 | 地质学类比 | 示例 | 依赖数据 |
|---|---|---|---|---|
| 节点 (Node) | ||||
| 网格节点 | 栅格化的一个单元 | 地图上的一个“点” | 1km x 1km 的网格单元 | 基础网格 |
| 实体节点 | 离散的地质对象 | 地质图上的一个“事物” | 一个岩体、一个矿床、一个钻孔 | 矢量/点数据 |
| 边 (Edge) | ||||
| 空间边 | 空间上相邻的节点 | “在...隔壁” | K-近邻 或 邻域连接 | 节点坐标 |
| 结构边 | 共享同一结构属性 | “在同一条断裂上” | 连接所有在“F1断裂”上的节点 | 断裂图(矢量) |
| 接触边 | 位于地质边界上 | “与...接触” | 连接岩体与围岩的边界节点 | 地质图(矢量) |
| 相似边 | 特征向量相似的节点 | “具有相似的地球化学特征” | 连接Cu/Mo比值高度相关的节点 | 节点特征数据 |
| 节点特征 | ||||
| 节点特征 | 节点(点或事物)的属性 | “该点的属性” | 磁异常值、Cu (ppm) 含量、岩性代码 | 物化遥数据 |
“建图”即特征工程
“建图”的过程,实际上就是一种更高级、更依赖地质知识的“特征工程”。在CNN中,地质学家提供的是数据层(如物探、化探图层);而在GCN中,地质学家不仅提供数据层(作为节点特征),还提供了对这些数据如何相互关联的假设(即边的定义)。
地质学家的“先验领域知识” 和“地质空间信息” 通过图的拓扑结构被编码 。GCN模型并不会凭空“发现”断裂的存在,而是地质学家告诉模型“这些节点同属于一条断裂”。GCN的任务,是在训练中学习这种被定义的“断裂关系”对于成矿预测的重要性。
“异质图” 代表了地质GCN的真正未来。它允许模型在一个统一的框架内处理“不同类型的地质实体” 。这意味着我们可以构建一个图,其节点包括“钻孔”(点)、“岩性多边形”(面)、“地球化学样品”(点)和“物探栅格单元”(格)。边可以表示它们之间真实的地质关系:“钻孔A穿过了岩体B”,“样品C位于B的下游”。这不再是一个简单的网格,这是一个真正“会思考”的“地质知识图谱” ,它模拟了地质学家综合分析多种来源数据时的思维过程。
GCN如何“思考”:聚合邻居的信息
GCN的核心机制(通常被称为“图卷积”)在技术上更准确的叫法是“信息传递”(Message Passing)。
GCN的“社交网络”
理解GCN工作原理最通俗的方式是“社交网络”比喻:
想要了解“你”(一个节点)的特性,不仅要看你自己的信息(如年龄、职业),更要看你的“朋友们”(通过边与你相连的邻居节点)的信息。GCN的功能就是让信息“沿着图的边传播”,允许节点“与它们的邻居节点交换信息” 。
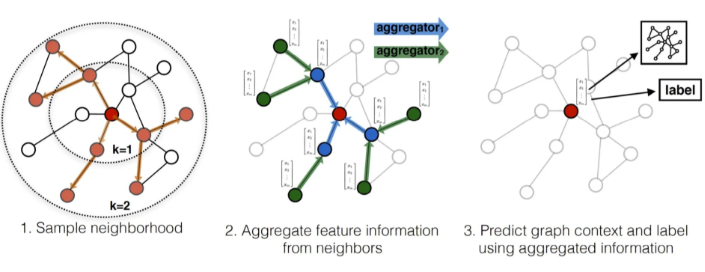
GCN的“卷积”:信息传递三步走
GCN的每一层都执行一个三步走的“信息传递”流程 。对于图中的任意一个节点 :
GATHER (收集): 节点 查找所有通过“边”与它直接相连的邻居节点(比如 和 )。它“收集所有邻居节点的嵌入(或信息)” 。
AGGREGATE (聚合): 节点 将来自邻居 和 的所有信息“收集并组合起来” 。这个聚合函数必须是“排列不变”的(即邻居的顺序不重要),通常采用简单的
SUM(求和)、MEAN(取均值)或MAX(取最大值)。UPDATE (更新): 节点 “使用聚合后的(邻居)信息来更新它们自己的表示” 。它将“聚合后的信息”与节点 当前的信息(来自上一层)相结合,然后通过一个神经网络层(更新函数)的处理,生成节点 在下一层的、全新的特征向量。
“深度”的意义:从“1度好友”到“全图感知”
GCN的“深度”(即层数)是理解其强大能力的关键。
1层GCN: 经过1轮信息传递,节点 聚合了它“1跳”(1-hop)邻居()的信息。它现在了解了它的“1度好友”。
2层GCN: 经过2轮信息传递,节点 再次聚合 和 的信息。但此时, 和 的特征向量已经包含了它们各自“1度好友”(比如 )的信息。因此,节点 间接地聚合了 和 (即它的“2跳”邻居)的信息。
K层GCN: “通过将信息传递GNN层堆叠在一起,一个节点最终可以整合来自整个图的信息” 。一个 层的GCN,其中心节点的“感受野”是在图结构上的 跳邻域。这就是GCN如何“捕捉...长程依赖关系” 的机制。
GCN的“深度”与CNN的“深度”在地质学上具有完全不同的含义。在CNN中,“深度”(更多层)意味着模型学习更抽象的视觉特征(例如,从像素 -> 边缘 -> 纹理 -> 形状)。
而在GCN中,“深度” 意味着模型拥有更广阔的关系感受野。一个1层的GCN只能进行局部思考。而一个5层的GCN,允许一个节点(例如一个成矿单元)的决策受到5个“结构跳数”之外的另一个节点(例如一个区域性控矿构造)的影响。GCN的“深度”就是模型从“局部思维”转向“区域思维”的能力,这完美地对应了地质学中的“区域成矿规律”等概念。
同时,这也凸显了第2节中“建图”的重要性。GCN的“聚合”步骤(如MEAN)在数学上非常简单 。如果图的边定义得不好,聚合步骤就会被“污染”。例如,一个代表“花岗岩体内部”的节点,如果错误地(通过空间边)连接到了岩体外的“围岩”节点,那么MEAN聚合操作将使这个花岗岩节点的特征向量被围岩信息“稀释”,导致更新后的信息毫无意义。
相反,如果我们只使用“岩性边”(仅连接其他花岗岩节点)和“结构边”(连接到附近的断裂节点),那么聚合操作将聚焦该节点的邻域信息,使其更新仅基于地质上相关的邻居。GCN的计算虽然简洁,但其“智能”的根源在于地质学家构建图谱时的“智慧”。
GCN 的优势
强大的非局部关系建模:这是GCN最核心的优势。它能够“捕捉复杂和非线性的空间关系” 以及“长程空间依赖关系”
天生的异构数据融合框架:对于 GCN,特别是“异质图神经网络”(HGNs),天生就是为解决这个问题而设计的。异质图“允许考虑各种关系并将合适的属性分配给各种类型的节点” 。
结语
GCN为真正的3D成矿预测提供了缺失的一环。一个3D地质模型(例如由GOCAD构建)在数据结构上本身就是一个3D网格(Mesh),也就是一个“图”。GCN可以直接在这种原生的3D网格上运行,而不需要像3D-CNN那样必须先将其“体素化”(Voxelization),或像2D-CNN那样必须将其“压扁” 。
这部分内容写的时候略微仓促,主要是把更多精力集中在视频翻译上了,提前预告,我开通了哔哩哔哩账户,在未来将会出一些实体的教程,还有一些研究前沿的研究会议精细化翻译搬运。欢迎关注

科学探索永无止境,本文仅为笔者个人学习总结。因知识所限,文中若有不当之处,敬请方家斧正。
